基于椭圆拟合的瞳孔中心精确定位算法研究

余 罗，刘洪英,，皮喜田，陈为民，许 帅，严 旭

1 重庆大学生物医学工程学院，重庆市， 400030

2 重庆市医疗电子工程技术研究中心， 重庆市， 40003

3 昆明学院， 昆明市， 650021

基于椭圆拟合的瞳孔中心精确定位算法研究

【作 者】余 罗1，刘洪英1,2，皮喜田1，陈为民3，许 帅1，严 旭1

1 重庆大学生物医学工程学院，重庆市， 400030

2 重庆市医疗电子工程技术研究中心， 重庆市， 40003

3 昆明学院， 昆明市， 650021

为了实现临床上精准视线跟踪的要求，提出了一种基于最小二乘法椭圆拟合的孔中心定位算法。首先在红外光源条件下，用摄像机捕获人眼图像，预处理后得到二值化图像，并提取图像轮廓，利用组成轮廓的像素点数100～300，对瞳孔进行粗过滤。对得到的系列轮廓随机选择6个点进行椭圆拟合，计算椭圆中心与边缘距离的方差，方差最小的为瞳孔中心。算法具有对存在白斑干扰及半闭眼状态时的瞳孔中心准确识别的优点。实验表明，该算法能够准确地定位瞳孔中心，且满足实时性要求。

视线跟踪；瞳孔中心；定位算法；椭圆拟合

0 引言

视线跟踪技术[1]在医学方面有着广泛应用，某些异常的眼动指标已被作为精神分裂症的生物标志物[2-3]，在LASIK手术中配备自动眼跟踪系统将大大提高手术的切削精度[4-5]。目前，基于图像处理的视线跟踪技术是主要的发展趋势，其中关键技术是对人眼瞳孔中心的识别。然而，由于瞳孔的形状不是一个规则的圆且易受到眨眼、睫毛、眼睑、角膜反射光斑等因素的干扰，增加了瞳孔中心检测的难度。在实际应用中，眼球的运动也对瞳孔检测的实时性提出了挑战。

Wildes结合圆形Hough变换的方法实现了对瞳孔与虹膜的边缘检测[6]，随后又出现了Hough变换的改进算法，提高了算法的速度与检测精度，但瞳孔为非正圆时识别率较低[7]。陈健等[8]提出了结合椭圆与参数传递的瞳孔检测方法，实现了动态和大遮挡情况下瞳孔中心的识别。尽管瞳孔检测已经取得不错的研究成果，但针对不同的应用，瞳孔检测的精确性和实时性仍有待提高。

鉴于此，本文提出了一种基于最小二乘法椭圆拟合的瞳孔中心定位算法：首先二值化眼睛图像并提取瞳孔轮廓，然后设定轮廓点数阈值为100～300，对瞳孔进行粗过滤，最后用最小二乘法椭圆拟合瞳孔轮廓并计算中心与边缘距离的方差，方差最小轮廓中心确定为瞳孔中心。实验结果表明该算法有较高的精度且满足实时性的要求。

1 椭圆表示与最小二乘法拟合

在二维平面坐标系中，椭圆一般可用圆锥曲线方程或平面坐标系的几何参数表示。椭圆方程的代数形式见式(1)，计算出5个未知数，即可确定该方程。

几何参数形式的的椭圆表示法涉及椭圆中心位置（xc, yc），长轴和短轴（a, b），长轴的转角θ等参数，两种形式的参数可用式(2)～(6)相互转换。

最小二乘法椭圆拟合是较常用的椭圆拟合方法，是由最大似然法推出的一个最优估计技术，它可使测量误差的平方和最小。最小二乘技术主要是寻找参数集合，从而最小化数据点与椭圆之间的距离度量。在求解椭圆方程(1)的过程中，为了避免出现零根，需要对参数做出限制，可设A+C=1。那么直接应用上述方程对边缘检测后的点进行最小二乘处理，就可以得到方程中的各个系数。即求目标函数：

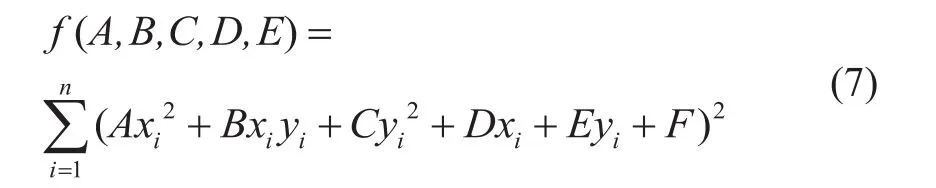
的最小值来确定各系数。如使f(A, B, C, D, E)的值为最小，由极值原理有：

由此可得一个线性方成组，然后应用全主元高斯消去法，结合约束条件，即可求出椭圆方程系数的值。

2 瞳孔中心定位算法研究

2.1 图像获取及灰度化

利用红外摄像机获取得到的RGB眼图中，颜色较深且近似为椭圆的部分为瞳孔，瞳孔与虹膜的边界清晰可见。RGB图占据的存储空间大小是灰度化后的3倍，且无法按照数学方法进行一些必要的处理（比如边缘检测或者二值化），故需将RGB模型转化为灰度值。常用的灰度化原理有RGB分量法、HSL分量法和HSV分量法等。本文采用的是RGB分量法，即将RGB通过不同的权值加权平均，可取得较好的图像灰度化结果。比如opencv函数库所采用的灰度权值如下：

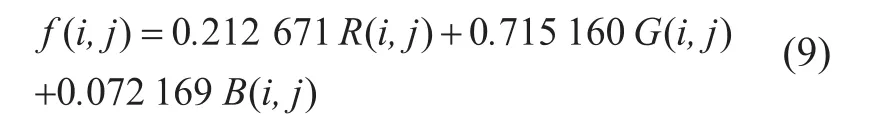
2.2 图像去噪

图像在拍摄的过程中，会不同程度地引入机械噪声、电子噪声和光学噪声等，其中光学噪声占较大比重。因此采用高斯滤波法对获取的眼图进行去噪处理。高斯滤波是对图像进行加权平均的一种线性平滑滤波，通常用一个模板扫描图像中的每一个像素，用模板确定的领域内像素的加权平均灰度值替代模板中心像素点的值。实际应用中模板大小的取值与σ的取值相关，如opencv中模板取值为：dim=1+2×(int(3.0×σ))。

2.3 图像二值化

为了提取瞳孔轮廓，需要将图像二值化，从而进一步识别瞳孔中心。其基本原理就是根据设定的阈值将目标图像上的像素点的灰度值置为0或255。如果某目标物体内部灰度值分布均匀，并且其处于其它等级灰度值均匀分布的背景下，采用阈值分割法就可以获得满意的分割效果。在图像处理过程中一般采用局部自适应阈值法，其基本原理是根据像素的相邻区域的像素值来判定该像素位置上的阈值。本文选择自适应阈值分割方法。其好处在于使每个像素位置处的二值化阈值都是根据其周围的相邻区域的像素值来决定，便于选取合适的阈值进行图像二值化分割。

2.4 瞳孔中心定位

眼图预处理后得到二值化图像，然后提取轮廓[9-10]，得到轮廓序列。但是在图像上找到的轮廓数目会有多个存在，如果要找到瞳孔轮廓就必须设置合适的过滤指标。在有效距离范围内，当眼睛与红外摄像机距离不同时，拍摄的眼图瞳孔轮廓大小随之变化。实验中经过对多张不同距离生成的眼睛图像瞳孔轮廓分析可知，组成瞳孔轮廓的像素点在100~300，可利用该指标对瞳孔轮廓进行粗过滤。

但是当图像质量较差时，获得的二值化图像不可避免有较多噪声，经瞳孔轮廓像素点数范围指标过滤后，得到的轮廓往往不止一个。通过对求取瞳孔中心坐标失败的图像分析可知，当某一区域噪声较多时，求取轮廓的函数会把它们作为一个大的轮廓，而不是分为几个较小的轮廓。但与近似椭圆的瞳孔的轮廓相比，它们的轮廓极不规则。因此对上一步求取到的轮廓用最小二乘法拟合得到椭圆。由式（2）可知，必须由不少于5个点的坐标才能求出参数(A, B, C, D, E, F)的值，但实际中往往需要6个点才能得到一个椭圆。因此将提取出轮廓特征点中任意6个点的坐标，代入式（2），求得5个参数值，然后拟合出椭圆轮廓，求出其中心。按照以上方法统计出所有的轮廓的中心，然后计算出中心点到轮廓边缘距离的方差，方差最小的轮廓，作为瞳孔的轮廓，相应椭圆的中心就作为瞳孔的中心。算法的具体步骤如下：

步骤1：采集眼睛图像并预处理；

步骤2：求取图像的轮廓；

步骤3：判断轮廓点的数目，如果数目N在100到300之间，保存轮廓到容器中；

步骤4：检查容器中轮廓的数量，如果数量Num为0，说明采集到的图像不符合要求，则返回至步骤1；如果Num等于1，则利用最二乘法椭圆拟合轮廓，并把椭圆中心作为瞳孔中心，算法结束；如果Num大于1，转步骤5；

步骤5：在所得的每个轮廓中，随机选择6个点，分别进行最小二乘法椭圆拟合，并计算所得到的椭圆中心与轮廓边缘各点的距离方差，把方差最小的轮廓作为瞳孔的轮廓，相应的椭圆中心作为瞳孔中心，算法结束。算法流程图如图1所示。

图1 瞳孔定位算法流程图Fig.1 The fl ow chart of pupil localization algorithm

3 实验结果与分析

瞳孔中心识别算法在以VC++6.0为平台的Intel(R) Core(TM) i5-4590 3.3 GHz 8 GB内存的PC机上编程实现。红外摄像头采样率为30 帧/s，图像大小1 600× 1 200（像素），实验在光线较暗的环境中，实验过程保持头部静止。眼睛完全张开时的瞳孔中心识别效果如图2所示（瞳孔中心用红色十字架标识）。图2（a）中的右上部分存在大面积的白色光斑，但由于瞳孔的像素值和白斑的像素值差别很大，通过算法的甄别，白色光斑不会对瞳孔中心定位造成影响。

图2 眼睛完全张开瞳孔中心识别Fig.2 Pupil center recognition in eyes wide open state

当眼睛半闭合时，瞳孔中心定位效果如图3所示。此时选取的图像虽然眼睛处于半闭状态，但仍能清晰地分辨出部分瞳孔，设计的算法仍可以完成瞳孔中心的定位，具有较强的抗干扰能力。

图3 眼睛半闭合瞳孔中心识别Fig.3 Pupil center recognition in eyes half closed state

表1是用手动标注和算法识别（对同一帧图像多次识别，数据取平均值）两种方式获取的图2（a）眼睛完全张开和图3半闭合状态时的瞳孔坐标数据。结果表明，算法识别所得到的坐标数据与手动标注得到的数据高度一致，该算法能够准确识别瞳孔中心。

表1 手动标注与算法识别精度比较Tab.1 Precision comparison between manual annotation and algorithmic recognition

此外，每帧图像的算法平均运行时间约为10.2 ms，能够满足实时系统的要求。在视线追踪过程中，视线方向是变化的，因此为了验证眼睛视线在不同方向时算法识别瞳孔中心的精度，设计了如图4所示不同方向的注视点图，其范围为1 280×720像素。对同一被试者，实验过程中每个注视点保持眼睛凝视不动，以确保瞳孔在图像中的相对坐标不变。每个注视点选取100帧图像数据进行统计分析。图5为注视中心点C时，100次识别得到的瞳孔中心坐标数据，横坐标在360.4到361.8之间变化，最大值与最小值之间的变化不大于1.4个像素，纵坐标在349.5到351.2之间变化，最大值与最小值之间的变化不大于1.7个像素。

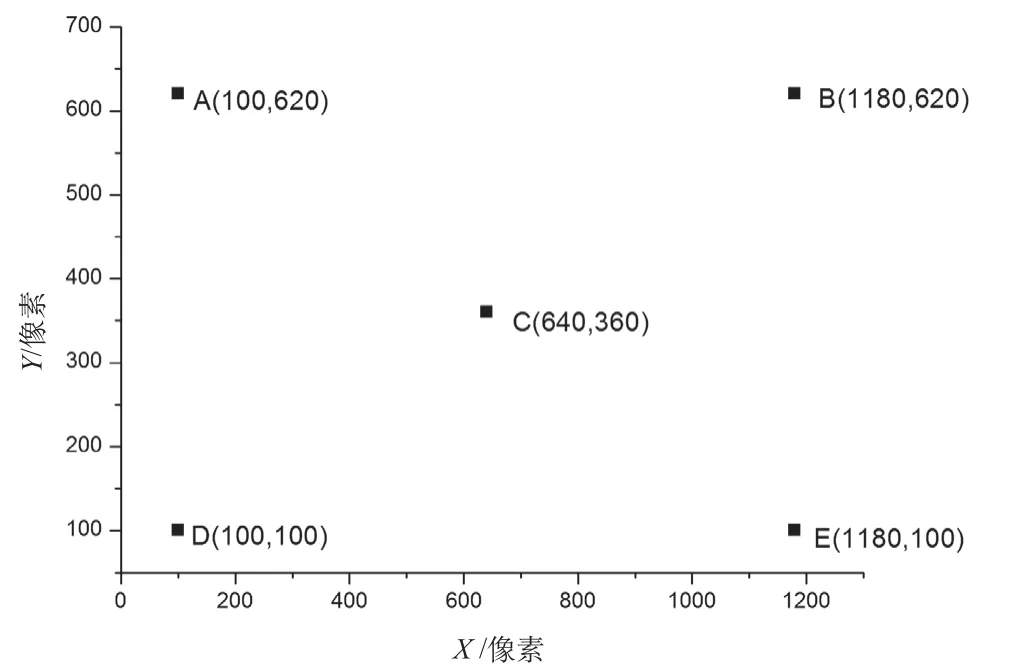
图4 注视点位置坐标Fig.4 Position coordinates of fi xation point

图5 100帧眼图瞳孔中心算法识别Fig.5 100 frame pupil center algorithm recognition

然后分别统计注视A、B、C、D、E点时瞳孔中心横坐标和纵坐标的平均误差和均方差，如图6和图7所示。实验表明，算法识别的瞳孔中心横坐标的平均误差不超过0.4像素，均方差不超过0.7像素；纵坐标平均误差不超过0.6像素，均方差不超过0.8像素。

图6 横坐标平均误差和均方差Fig.6 The average error and mean standard deviation of the horizontal coordinate

图7 纵坐标平均误差和均方差Fig.7 The average error and mean standard deviation of the vertical coordinate

4 结论与讨论

实验证明本文提出方法的有效性，能够满足视线追踪所要求的瞳孔中心快速准确定位[11]。首先，本方法对图像的质量要求不高，对光照情况下瞳孔内出现白斑的情况不影响对瞳孔中心的识别；其次，对眼睛半闭合而瞳孔无法完全显现时的情况，本文提出的方法仍能精确定位瞳孔中心。然而本文提出的方法还有改进之处，由于算法是对整个眼图进行处理，增加了检测的时间，因此可进一步结合下采样与近似下采样方案[12]缩小待处理的原始图像，或者利用改进的阈值法在图像上选择一个包括全部瞳孔的区域作为感兴趣的图像[13]，用于后续的处理，从而进一步提高算法检测速度。另一方面，获取更高质量的眼图以减小噪声，从而减少伪轮廓的获取，提高检测精度和算法运行时间。瞳孔中心的准确识别能够为后续眼动仪的研制奠定良好的基础，有利于促进眼动分析在临床中的应用[14-15]。

[1] 温晴川, 达飞鹏, 方旭. 基于双目立体视觉的视线跟踪系统标定[J]. 光学学报, 2012(10): 152-162.

[2] Franco J G, De P J, Gaviria A M, et al. Smooth pursuit eye movements and schizophrenia: literature review[J]. Arch Soc Esp Oftalmol, 2014, 89(9): 361-367.

[3] Delerue C, Hayhoe M, Boucart M. Eye movements during natural actions in patients with schizophrenia[J]. J psychiatry neurosci, 2013, 38(3): 317-324.

[4] Lazon D L J P. Visual and non-visual factors associated with patient satisfaction and quality of life in LASIK[J]. Eye, 2011, 25(9): 1194-1201.

[5] Yong H K, Kang S Y, Jin Y C, et al. Laser refractive surgery using an active eye-tracking system in congenital nystagmus[J]. J Korean Ophthalmol Soc, 2015, 56(12): 1991-1996.

[6] Ganorkar S R, Ghatol A A. Iris recognition: an emerging biometric technology[C]. P IEEE, 2007: 1348-1363.

[7] 付琰, 卢荣胜, 夏瑞雪, 等. 基于重要性采样的随机Hough变换圆检测算法[J]. 电子测量技术, 2012, 35(5): 45-48.

[8] 陈健, 郑绍华, 潘林, 等. 结合椭圆拟合与参数传递的瞳孔检测方法[J]. 仪器仪表学报, 2014 (8): 1890-1899.

[9] 田野, 王怀军, 方志良. 基于形态学重构算法的瞳孔精确检测[J].光电子·激光, 2008, 19(3): 409-411.

[10] 苑玮琦, 林忠华, 徐露. 一种快速而准确的虹膜定位算法[J]. 光电子·激光, 2007, 18(6): 729-733.

[11] Dong W H, Liao H, Fang X U, et al. Using eye tracking to evaluate the usability of animated maps[J]. Sci China Earth Sci, 2014, 57(3): 512-522.

[12] 邱勇. 人眼虹膜图像检测与提取方法[J]. 计算机仿真, 2011, 28(11): 250-254.

[13] 潘林, 魏丽芳, 郑炳锟, 等. 改进的遮挡条件下瞳孔检测方法[J].中国图象图形学报, 2012, 17(2) : 76-82.

[14] Pierce K, Marinero S, Hazin R, et al. Eye tracking reveals abnormal visual preference for geometric images as an early biomarker of an autism spectrum disorder subtype associated with increased symptom severity[J]. Biol Psychiatry, 2015, 15(8): 657-666.

[15] Chita-Tegmark M. Attention allocation in ASD: a review and metaanalysis of eye-tracking studies[J]. Res Dev Disabil, 2016, 48: 1-15.

Research on Exact Location Algorithm of Pupil Center Based on Ellipse Fitting

【Key words 】YU Luo1, LIU Hongying1,2, PI Xitian1, CHEN Weiming3, XU Shuai1, YAN Xu1
1 School of Biomedical Engineering, Chongqing University, Chongqing, 400030
2 Key Laboratories for National Defense Science and Technology of Innovative Micro-Nano Devices and System Technology, Chongqing University, Chongqing, 400030
3 Kunming University, Kunming, 650214

eye-tracking, pupil center, location algorithm, ellipse fi tting

TP391

A

10.3969/j.issn.1671-7104.2017.03.004

1671-7104(2017)03-0170-05

2016-11-03

国家科技支撑计划项目（2013BAI03B04；2015BAI01B14）

刘洪英，副教授，E-mail: liuhongying@cqu.edu.cn

【 Abstract 】In order to realize the requirement of precise eye tracking in clinical, a pupil center location algorithm based on the least square method is proposed. First, the eye image was captured by the camera under the infrared light, and then the two-valued image was obtained after preprocessing. Use the number of pixels that form the outline which was Extracting from the two-valued image to carry out the rough fi ltration of the pupil. The ellipse curve was fi tting by the randomly select 6 pixels on the fi ltered contours, and then calculated the variance of distance between the center and the edge of the ellipse. The ellipse center is ellipse center, where the variance of the distance is Minimum. The algorithm has advantage of accurate identi fi cation the pupil center when there is white spot interference and squint. Experiments show that the pupil center can be located quickly and real-timely by this algorithm.