基于生物启发的水下机器人路径跟踪控制

邓志刚，袁芳，朱大奇



基于生物启发的水下机器人路径跟踪控制

邓志刚，袁芳，朱大奇

(上海海事大学水下机器人与智能系统实验室，上海，201306)

针对常规反步控制方法在路径跟踪中出现的速度跳变与推进器驱动饱和等问题，将生物启发神经动力学模型应用到水下机器人路径跟踪控制中。利用生物启发神经动力学模型的渐变和有界输出等特性，设计基于生物启发的反步路径跟踪控制器，并同传统反步跟踪控制器进行对比分析。仿真结果表明：在较大的初始跟踪误差下，所设计的跟踪控制器可以有效克服水下机器人跟踪控制中的速度跳变，避免推进器的驱动饱和，满足水下机器人推进器的推力约束。

水下机器人；自治−遥控机器人；反步控制；生物启发神经动力学；路径跟踪

水下机器人为了完成指定任务，必须执行控制器发出的指令，按照人类的设想进行各种操作。机器人的控制技术涉及面很广，不同类型机器人的控制方法也有明显不同。对遥控水下机器人而言，主要还是靠人来完成一些高难度的操作，控制程序只涉及完成一些辅助动作，比如自动定深、自动定向和自动定速等。但对于自治水下机器人而言，不仅要能完成比较复杂的搜索、跟踪和水下救援，而且要具有比较高的智能，以便在复杂的环境下作出判断，并有效地完成指定任务。水下机器人的控制方法有很多，基本分为线性模型控制、非线性模型控制和无模型控制，主要包括PID(proportion integration differential)控制[1−4]、滑模控制[5]、线性二次高斯闭环转移恢复控制[6−7]、模糊滑模控制[8]、反步控制[9]、神经网络控制[10−12]、模型预测控制[13−14]和自适应控制[15]等。反步控制在机器人控制领域得到了广泛应用，它是一种基于Lyapunov函数的递归设计，其基本思路是将复杂的非线性系统，分解成若干个不超过系统阶数的子系统，然后为每个子系统设计部分Lypaunov函数和中间虚拟控制量，通过确定适当的虚拟反馈，使得系统的前面状态达到渐近稳定，一直“反推”至整个系统，从而实现整个系统的渐近镇定。作为一种计算简单和系统稳定的控制方法，但也存在重要不足，即在控制误差较大时，存在机器人速度跳变问题。这时水下机器人需要具备超大的加速度和驱动力(力矩)，甚至无穷大，这在实际机器人控制中是无法实现的。在跟踪控制问题上，路径跟踪与轨迹跟踪的主要区别在于跟踪轨迹是否与时间相关，前者参考轨迹与时间无关，后者与时间相关，路径跟踪可以看作是轨迹跟踪的一种特例，具体可参见文献[16−19]。本文作者针对反步路径跟踪控制算法引起的速度跳变，引起水下机器人跟踪加速度和驱动力(力矩)出现的饱和问题，使用生物启发模型对反步方法进行改进，提出一种基于生物启发模型的反步路径跟踪控制方法。在反步方法中加入生物启发模型平滑速度跳变，解决水下机器人推进器的推力超限问题。通过跟踪典型曲线轨迹的对比仿真实验，证明所提方法的有效性。

1 动力学建模

1.1 SMU I ARV机器人简介

目前在海洋工程中常用的有两类无人水下机器人：遥控水下机器人(ROV)和自治水下机器人(AUV)。自治−遥控水下机器人(ARV)是一种复合型水下机器人，在经济性、灵活性和活动范围方面优于传统ROV。它既可以像ROV一样进行手动操控，又能像AUV一样根据预编程指令在几公里的范围内进行巡航搜索。

“SMU I”ARV作为上海海事大学水下机器人与智能系统实验室(LUVIS)的试验研究平台，主要用于系统硬件的设计评估和控制算法的水池试验验证等方面研究。“SMU I”ARV能够进行4个自由度(纵向、艏向、潜浮和纵倾)的运动，而侧移和横摇自由度的运动呈现被动稳态[20]，该机器人技术参数如表1所示。

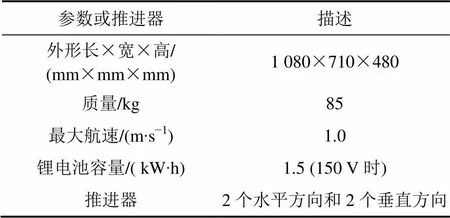
表1 SMU I ARV主要技术参数

1.2 SMU I ARV机器人动力学建模

“SMU I”ARV在推进器的作用下可实现4自由度的运动，即纵向、艏向、潜浮和纵倾。推进器的位置参数如表2所示，推进器布置如图1所示。L为水下机器人的艉推力臂，L和L为垂推的前后力臂。根据力与力矩作用原理，可计算出“SMU I”ARV在各个自由度上产生的合力与合力矩[9]。

表2 SMU I ARV推进器的位置参数

图1 SMU IARV推进器布置图

该机器人的平移运动有纵向和潜浮，回转运动只有艏向和纵倾，忽略侧移和横摇运动。由于其运动速度在1.0 m/s以下，所以科氏及向心力可以忽略。其主要运动方式为单自由度运动，且各自由度之间的一阶、二阶黏性类耦合系数较小，并假定载体坐标系的原点位于水下机器人的重心，由此“SMU I”ARV的动力学模型可以简化为

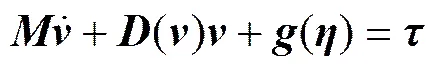
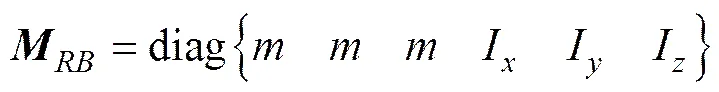
式中：I，I和I为转动惯量；，，，，和为加速度系数。

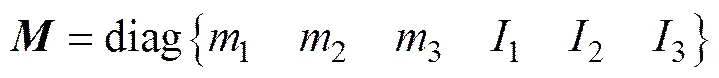
式中：X，Y，Z，，和为速度系数；，，，，和为角速度系数。

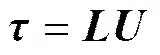
其中：

；。

又据

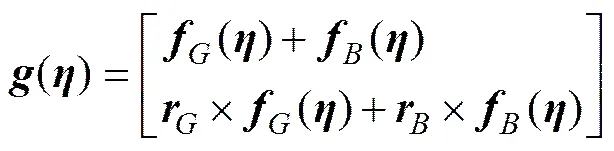
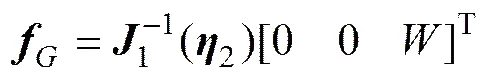
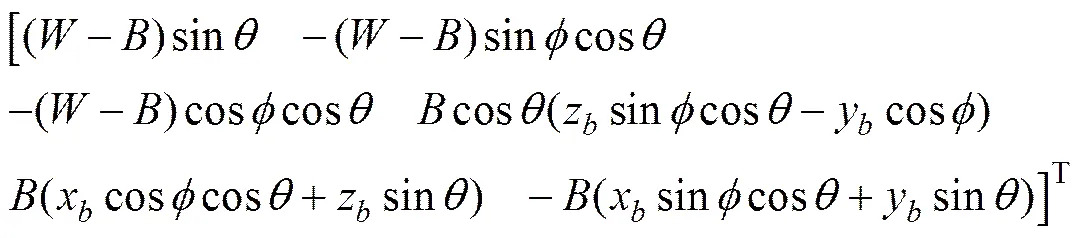
式中：为重力；为浮力。由此在载体坐标系下，对通用6自由度动力学模型简化后，可得“SMU I”ARV的6自由度动力学模型，如下式所示：

(4)

注意到式(4)的最后2个方程中，和并不会受到的作用，而且水动力参数，，和是负的。因此，和自由度的动力学方程是被动稳定的，非线性的控制不会影响和，但是，在运动学上，和对位置的影响需考虑。

在路径跟踪控制研究中采用式(4)中第1式和第4式，它们是“SMU I”ARV纵向和艏向自由度动力学模型。在假定其纵倾角0°和横摇角0°的条件下，这时相应的单自由度模型还可以进一步简化为

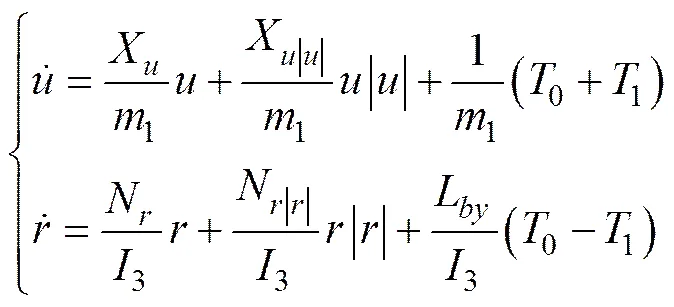
2 生物启发反步控制

2.1 虚拟跟踪描述

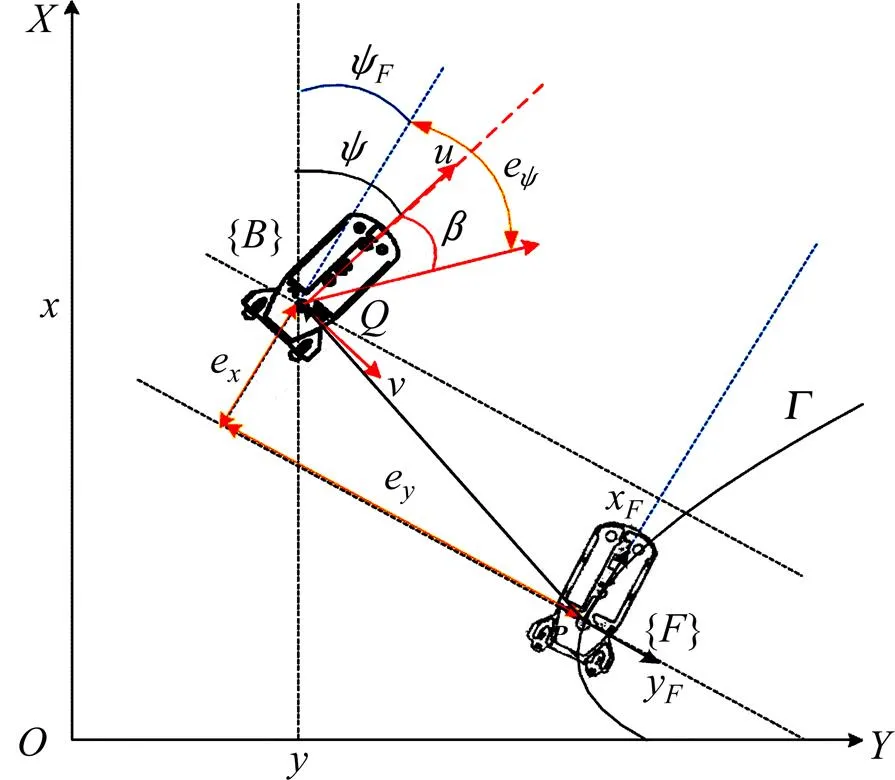
图2 水下机器人虚拟跟踪坐标系

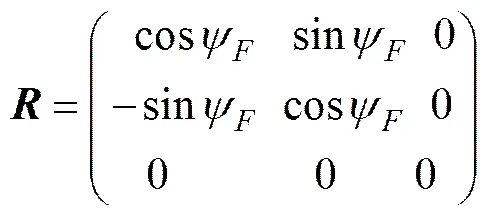
(7)

经过复杂坐标系转换，得到误差e和e的导数如式(8)，相关的证明过程见文献[22]。

(9)

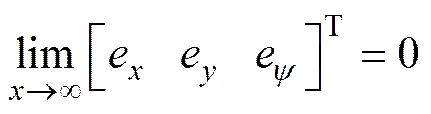
即位姿误差全局逐渐收敛于0，纵向速度逐渐收敛于期望纵向速度u。

2.2 反步路径跟踪控制器设计

反步路径跟踪控制方法分2步：第1步，进行运动学控制设计，满足逐步趋近的条件；第2步，进行动力学控制设计，并保证系统达到全局的性能指标。

2.2.1 运动学控制设计

为了描述ARV跟踪时姿态角误差的变化，引入SAMSON等[23]设计的期望角：

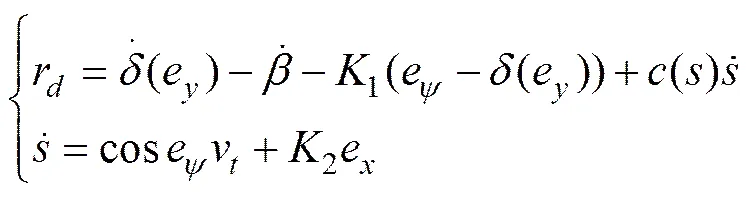
其中：控制参数1＞0，2＞0。

使用Barbalat引理[25]，可以证明上述运动学路径跟踪的有效性。Barbalat引理为：若二阶可导并且当时连续，则当时，趋近于0。

引入Lyapunov函数：

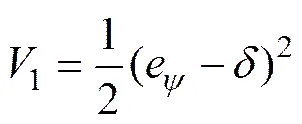
将式(9)代入函数1，得到。因此，1为单调递减函数，存在且有界。因，并且有界，故是连续的。由于1符合应用Barbalat引理的条件，所以，得到，即，也就是ARV的姿态角误差将逐渐收敛于期望角，同时变量，和均有界。

引入Lyapunov函数：

(15)

2.2.2 动力学控制设计

在进行动力学控制律设计时，把运动学参考输入r，以及参考纵向速度u作为动力学的参考输出，寻找需要产生控制力和力矩的控制律，使和分别收敛于r和u。假定纵向速度跟踪误差，艏向速度跟踪误差为，构造Lyapunov函数：

式(16)的导数为

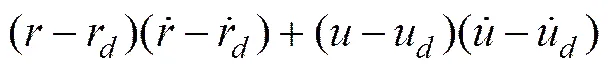
设计的动力学控制律如下式(18)，相关的内容参见文献[26]：

(18)

其中：3＞0；4＞0；5＞0；；。

从式(18)和式(5) 动力学模型可知：

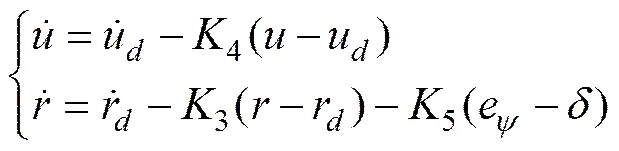
将式(19)代入式(17)，可得

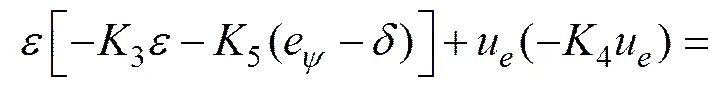
(20)

由2和可知：2为单调递减函数，存在且有界，有界，是连续的。2满足Barbalat引理的条件，所以。可见：实际机器人在式(18)动力学控制律作用下，纵向速度和艏向速度将收敛于u和r，路径跟踪误差全局渐近稳定。

2.2.3 生物启发神经动力学模型

1963年，HODGKIN等[27]研究了枪乌贼巨大神经轴突的动作电位，揭示了电位变化的内在机制与规律，并得到该类神经冲动的经典数学模型，其神经系统中细胞膜的膜电压V的动态特性方程可表示为

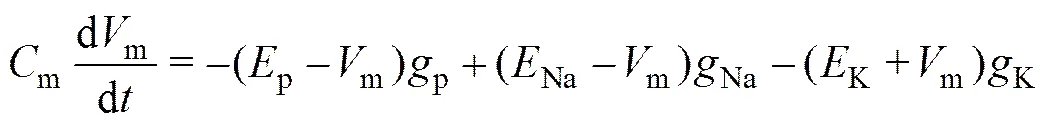
其中：m为细胞膜电容；K，Na和p分别为细胞膜中钾离子、钠离子和无源漏电流的饱和电势；k，Na和p分别为钾、钠和无源通道的电导。

GROSSBERG[28]将式(21)进行简化，定义，，，，，和，得到如下生物启发神经动力学模型：

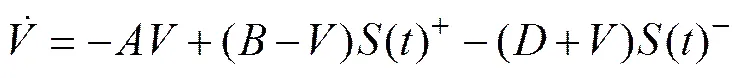
其中：为神经元的细胞膜电势；，和分别为衰减率和神经元活动的上下限，为非负常数；和分别表示神经元的激励和抑制输入。式(22)是一个连续且可导的等式，表征了单个神经元的动力学动态特性。

2.2.4 生物启发反步跟踪控制算法

在动力学反步路径跟踪控制中，在机器人运动的初始时刻往往会发生速度跳变，这种跳变会导致推进器系统需要产生过大的力和力矩，从而超出推进器推力的最大饱和值。针对这个问题，考虑到生物启发神经动力学模型可以使误差输出变得平滑和有界，从而获得平滑和符合物理约束的速度、力和力矩，为此定义第个模型的输出为

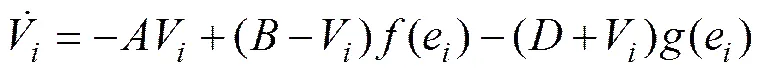
(25)

3 仿真实验

进行平面曲线路径跟踪仿真实验。预定跟踪曲线起点坐标为(0, 20)点，跟踪路径以惯性坐标系的横坐标为曲线的描述参数，以式(26)描述的跟踪路径进行仿真实验研究。

其中：=50；=5；=4；=4；控制参数；；；；；；；初始状态；(0)=0 m/s；(0)=0 m/s；(0)=0 rad/s和u= 0.3 m/s。曲线跟踪的仿真实验结果如图3所示。从图3可以看到：水下机器人能缓慢靠近预定的路径，同时，位移和姿态角误差随着仿真时间逐渐减小。当水下机器人跟踪上曲线路径后，可通过控制它的纵向速度和艏向速度，就能准确地跟踪曲线路径。从2种方法跟踪曲线来看，生物启发方法比传统反步方法更平滑地到达预定的路径。

图4~6所示分别为跟踪误差、纵向和艏向速度，以及力和力矩等参量之间的对比。从图4可以看出：生物启发方法对位移误差，和姿态角误差的变化过程和反步方法也是有区别的，尤其反步方法的角度误差在开始时出现明显振荡，而生物启发方法的位移误差和姿态角误差趋近过程更为平稳。水下机器人的纵向速度和艏向速度的变化趋势如图5所示，在跟踪的初始阶段，水下机器人和跟踪路径相互之间的跟踪误差较大，导致2种方法在初始速度变化上有明显不同。在纵向速度方面，反步方法中出现了比较大的速度突变，它的纵向速度起始点是 −0.8 m/s，而生物启发方法的纵向速度起点是0 m/s。在艏向速度方面，在反步方法中出现了比较大的艏向速度突变，它的艏向速度起始点是0.3 rad/s，而生物启发方法的艏向速度起点是0 rad/s。从这2方面可以看出：生物启发方法可以抑制或减小速度跳变，有效避免过大速度的产生，以免超出实际推进器推力的物理饱和特性。这一点也可以从图6得到体现，比如反步方法初始力为−400 N，而生物启发初始力为100 N，反步方法的力已经超出推进器所能提供的最大推力，所以，生物启发方法消除了速度跳变及其引起的过大的力和力矩，表3所示为2种跟踪方法的主要参数。

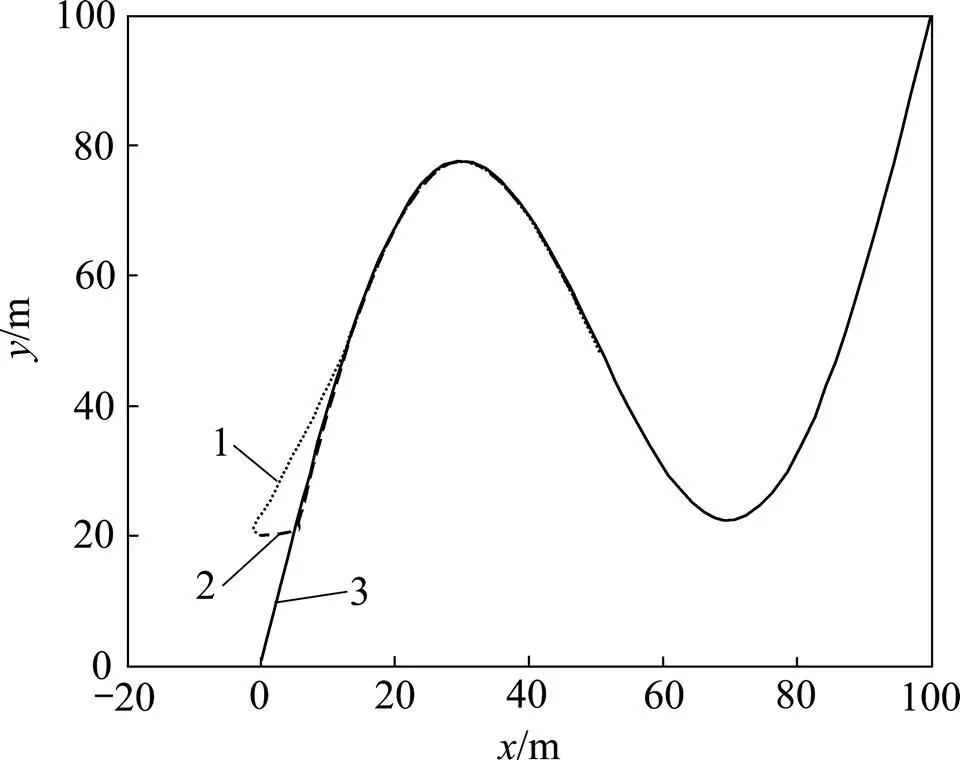
1—生物启发方法；2—传统反步方法；3—预定跟踪路径。

(a) ex；(b) ey；(c)

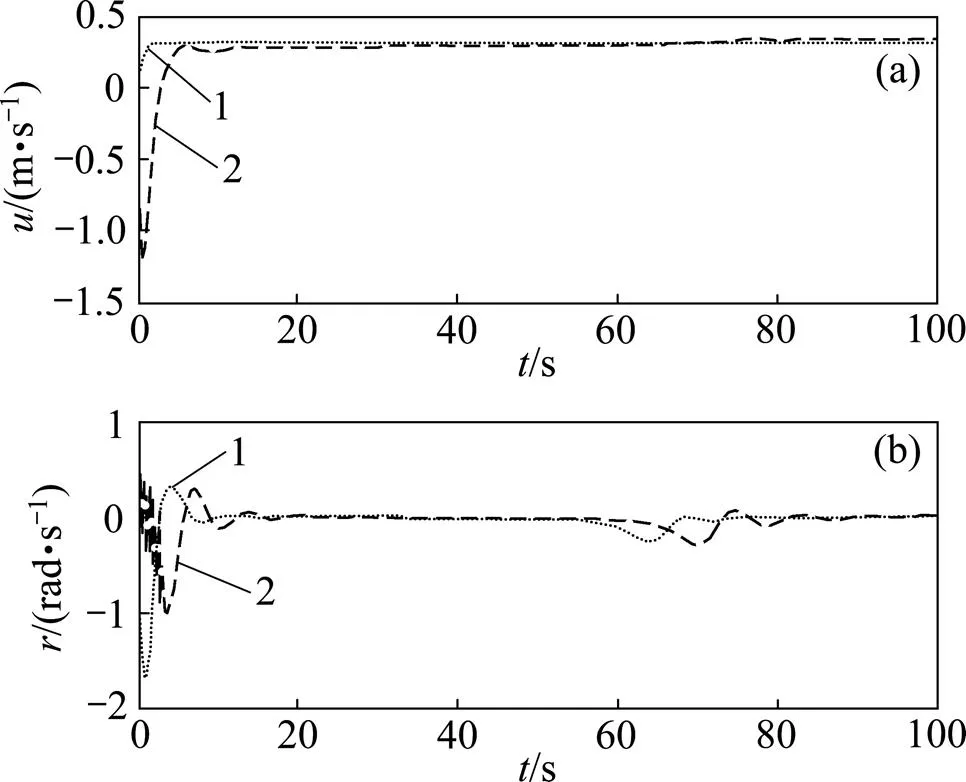
(a) u；(b) r

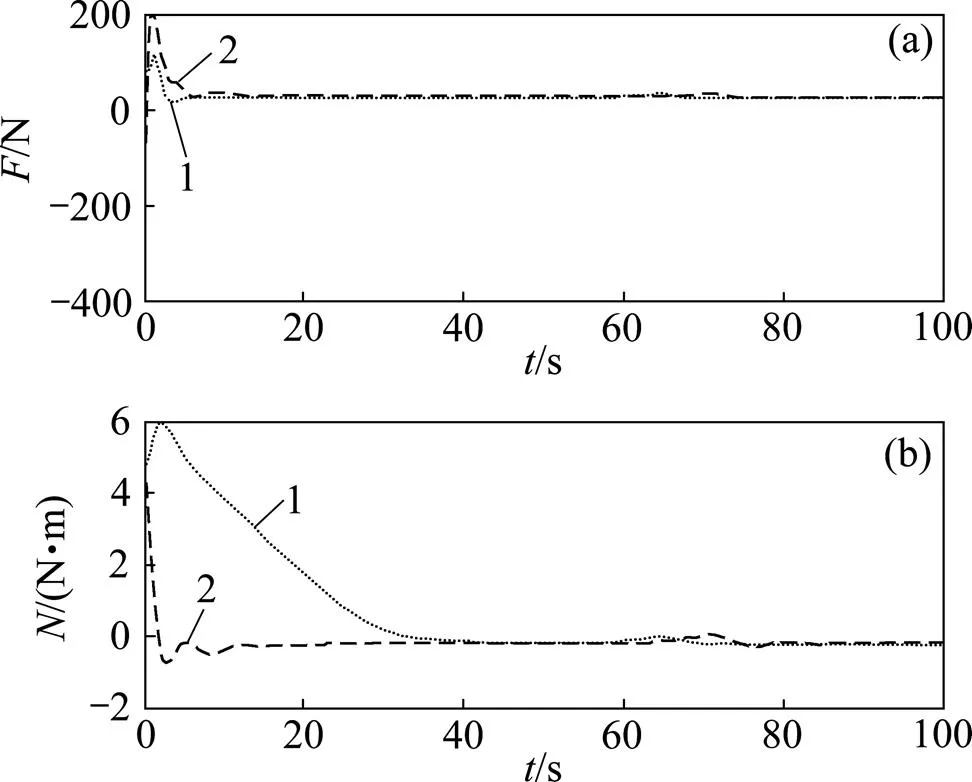
(a) F；(b) N

表3 2种跟踪方法的主要参数(初始时刻)

4 结论

1) 研究水下机器人在海底工程应用的路径跟踪问题，并以“SMU I”ARV为研究对象，从动力学角度进行反步路径跟踪控制，并结合生物启发神经动力学模型，使得输出速度平滑，从而避免速度的跳变，使得水下机器人在初始阶段获得不超过推进器物理饱和范围的力和力矩。

2) 生物启发反步路径跟踪控制算法不但可以消除跟踪初始阶段的速度跳变，而且降低水下机器人推进器发生故障的几率，延长推进器的使用寿命。

[1] RENTSCHLER M E, HOVER F S, CHRYSSOSTOMIDIS C. System identification of open-loop maneuvers leads to improved AUV flight performance[J]. IEEE Journal of Oceanic Engineering, 2006, 31(1): 200−208.

[2] RENTSCHLER M E, HOVER F S, CHRYSSOSTOMIDIS C. Modeling and control of an Odyssey III AUV through system identification tests[C]// Proceedings of the Unmanned Untethered Submersible Technology Conf. Durham, NH, 2003: 1−13.

[3] GONZALEZ L A. Design, modelling and control of an autonomous underwater vehicle[D]. Crawley WA: University of Western Australia. School of Electrical, Electronic and Computer Engineering, 2004: 71−85.

[4] MARVIAN MASHHAD A, MOUSAVI MASHHADI S K. PID like fuzzy logic control of an unmanned underwater vehicle[C]// 2013 13th Iranian Conference on Fuzzy Systems (IFSC). Qazvin: IEEE, 2013: 1−5.

[5] JOONYOUNG K, KIHUN K, CHOI H S, et al. Depth and heading control for autonomous underwater vehicle using estimated hydrodynamic coefficients[C]// OCEANS'2001 MTS/ IEEE Conference and Exhibition. Honolulu: IEEE, 2001: 429−435.

[6] ADRIAN I F. Simulation, modeling and control of a near-surface underwater vehicle[D]. Vancouver:University of British Columbia. Dept of Mechanical Engineering, 2000: 86−121.

[7] OSTAFICHUK P M. AUV hydrodynamics and modeling for improved control[D]. Vancouver: University of British Columbia. Dept of Mechanical Engineering, 2004: 159−169.

[8] 于华男. 开架式水下机器人辨识与控制技术研究[D]. 哈尔滨: 哈尔滨工程大学船舶工程学院, 2003: 41−51. YU Huanan. Research on identification and control of an open- frame underwater vehicle[D]. Harbin: Harbin Engineering University. College of Shipbuilding Engineering, 2003: 41−51.

[9] VLADIMIR D. Unifying behavior based control design and hybrid stability theory for AUV application[D]. University of California Riverside. Department of Electrical Engineering, 2009: 72−105.

[10] WANG Jianguo. Neural network identification of underwater vehicle with hybrid learning algorithm[C]// 2012 31st Chinese Control Conference (CCC). Hefei, China: IEEE, 2012: 1922−1925.

[11] 段群杰, 张铭钧. 一种自适应神经模糊运动规划器设计[J]. 传感器与微系统, 2007, 26(2): 58−64. DUAN Qunjie, ZHANG Mingjun. Design of motion planner based on fuzzy adapted nerve network[J]. Transducer and Microsystem Technologies, 2007, 26(2): 58−64.

[12] LIANG Xiao, PANG Yongjie, WAN Lei, et al. Dynamic modelling and motion control for underwater vehicles with fins[C]// INZARTSEV A V. Underwater Vehicles. Vienna: InTech, 2009: 539−556.

[13] JAGTAP P, RAUT P, KUMAR P, et al. Control of autonomous underwater vehicle using reduced order model predictive control in three dimensional space[J]. Ifac Papersonline, 2016, 49(1): 772−777.

[14] 徐建安. 水下机器人动力学模型辨识与广义预测控制技术研究[D]. 哈尔滨: 哈尔滨工程大学机电工程学院, 2006: 57−83. XU Jianan. Research on dynamical model identification and generalized predictive control of autonomous underwater vehicle[D]. Harbin: Harbin Engineering University. College of Mechanical and Electrical Engineering, 2006: 57−83.

[15] van de VEN P W J, JOHANSEN T A, SOENSEN A J, et al. Neural network augmented identification of underwater vehicle models[J]. Control Engineering Practice, 2007, 15(6): 715−725.

[16] 韩庆珏, 刘少军. 深海履带车的路径跟踪控制算法[J]. 中南大学学报(自然科学版), 2015, 46(2): 472−478. HAN Qingjue, LIU Shaojun. Path tracking control algorithm of the deep sea tracked vehicle[J]. Journal of Central South University (Science and Technology), 2015, 46(2): 472−478.

[17] 万磊, 张英浩, 孙玉山, 等. 欠驱动智能水下机器人的自抗扰路径跟踪控制[J]. 上海交通大学学报, 2014, 48(12): 1727−1738. WAN Lei, ZHANG Yinghao, SUN Yushan, et al. ADRC path-following control of underactuated AUVs[J]. Journal of Shanghai Jiao Tong University, 2014, 48(12): 1727−1738.

[18] 王宏健, 陈子印, 贾鹤鸣, 等. 基于滤波反步法的欠驱动AUV三维路径跟踪控制[J]. 自动化学报, 2015, 41(3): 631−645. WANG Hongjian, CHEN Ziyin, JIA Heming, et al. Three- dimensional path-following control of underactuated autonomous underwater vehicle with command filtered backstepping[J]. Acta Automatica Sinica, 2015, 41(3): 631−645.

[19] ZHANG Guoqing, ZHANG Xianku. Concise robust adaptive path-following control of underactuated ships using DSC and MLP[J]. IEEE Journal of Oceanic Engineering, 2014, 39(4): 685−694.

[20] 蒋新松, 封锡盛, 王棣棠. 水下机器人[M]. 沈阳: 辽宁科学技术出版社, 2000: 360−375. JIANG Xinsong, FENG Xisheng, WANG Litang. Unmanned underwater vehicles[M]. Shengyang: Liaoning Science and Technology Publishing House, 2000: 360−375.

[21] LAPIERRE L, SOETANTO D. Nonlinear path-following control of an AUV[J]. Ocean Engineering, 2007, 34(11/12): 1734−1744.

[22] SOETANTO D, LAPIERRE L, PASCOAL A. Adaptive, non-singular path-following control of dynamic wheeled robots[C]// IEEE 42nd Conference on Decision and Control. Lisboa, Portugal: IEEE, 2003: 1765−1770.

[23] SAMSON C, ABDERRAHIM A. Mobile robot control part 1: feedback control of a non-holonomic mobile robot[R]. INRIA Sophia-Antipolis: INRIA, 1991: 12−58.

[24] 施淑伟, 严卫生, 高剑, 等. 常值海流作用下的AUV水平面路径跟踪控制[J]. 兵工学报, 2010, 31(3): 375−379. SHI Shuwei, YAN Weisheng, GAO Jian, et al. Path-following control of an AUV in the horizontal plane with constant ocean currents[J]. Acta Armamentarii, 2010, 31(3): 375−379.

[25] HOU Mingzhe, DUAN Guangren, GUO Mengshu. New versions of Barbalat’s lemma with applications[J]. Journal of Control Theory and Applications, 2010, 8(4): 545−547.

[26] LAPIERRE L, SOETANTO D, PASCOAL A. Nonsingular path following control of a unicycle in the presence of parametric modeling uncertainties[J]. International Journal Robust Nonlinear Control, 2006, 16(10): 485−503.

[27] HODGKIN A L, HUXLEY A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. Bulletin of Mathematical Biology, 1990, 52(1/2): 25−71.

[28] GROSSBERG S. Nonlinear neural networks: principles, mechanisms, and architectures[J]. Neural Networks, 1988, 1(1): 17−61.

(编辑 陈爱华)

Bio-inspired path following control for underwater vehicles

DENG Zhigang, YUAN Fang, ZHU Daqi

(Laboratory of Underwater Vehicles and Intelligent Systems,Shanghai Maritime University, Shanghai 201306, China)

To solve the speed jump and propeller-driven saturation problems in the conventional backstepping method, the bio-inspired neuraldynamic model was applied to the path following control for underwater vehicles. With gradient and bounded-output characters of bio-inspired neuraldynamic model, the bio-inspired backstepping path following controller was designed and comparison study and analysis with conventional backstepping controller are conducted. Through the simulation results, in the large initial tracking error condition, the proposed tracking controller can deal with speed jump and avoid driving saturation to meet propeller thrust constraints.

underwater vehicle; autonomous remotely-operated vehicle(ARV); backstepping control; bio-inspired neurodynamics; path following

10.11817/j.issn.1672-7207.2017.05.016

TP273

A

1672−7207(2017)05−1234−08

2016−07−09；

2016−09−22

国家自然科学基金资助项目(51409156，51279098)；上海市科委创新行动计划项目(14JC1402800) (Projects(51409156, 51279098) supported by the National Natural Science Foundation of China; Project(14JC1402800) supported by Creative Activity Plan for Science and Technology Commission of Shanghai)

邓志刚，博士，工程师，从事水下机器人建模及控制算法研究；E-mail: dzg1026@126.com