磁控热防护系统高温流场与电磁场耦合计算方法
李 开,柳 军,刘伟强
(国防科学技术大学航天科学与工程学院,长沙410073)
磁控热防护系统高温流场与电磁场耦合计算方法
李 开,柳 军,刘伟强
(国防科学技术大学航天科学与工程学院,长沙410073)
为了研究真实气体条件下霍尔效应对磁流体(MHD)控制热防护效果的影响,建立了热化学非平衡流场、外加磁场、霍尔电场的耦合计算方法。分析了耦合计算效率与电场更新间隔、电势残差收敛极限的关系。给出了采用非平衡霍尔系数模型时电场更新间隔和电势收敛极限的较优取值。研究表明,当霍尔系数较小(β=1.0)时,电场更新间隔大于100流场计算时间步时耦合计算效率较高,且导电壁面和绝缘壁面结论一致。当霍尔系数较大时,耦合计算时间过长,可适当增加电场迭代间隔和电势收敛极限以提高耦合计算效率。
磁流体控制;热防护;霍尔电场;耦合计算
0 引 言
临近飞行器在高超声速飞行时气动热问题日趋严重,其“热障”问题已成为制约飞行器设计的瓶颈[1-3]。最近十年间高超声速领域的新概念热防护技术层出不穷。得益于近年来电磁流动控制技术、超导磁铁技术的进步[4-5],磁控热防护技术的现实可行性逐渐增强,应用价值逐年提高,得到了各国研究者的普遍关注[6-7]。但值得注意的是,在典型轨道再入及超轨道再入飞行条件下,霍尔效应明显,感应产生的霍尔电场会改变前缘流场电流分布,进而改变洛伦兹力,影响磁控热防护系统的效率。磁控热防护系统的霍尔效应研究涉及外加磁场、感应电场和非平衡流场三场的耦合计算,是该领域研究的难点[8]。
由于高超声速飞行器前缘激波后电离度较低,低磁雷诺数假设往往可以得到满足[9]。此时,外加磁场、感应电场与非平衡流场的耦合可以通过耦合求解电势泊松方程和非平衡磁流体方程实现。由于大霍尔系数条件下电场求解刚性严重、收敛性差[10],电磁场和热化学非平衡流场的耦合计算效率较低。在现有文献的研究中,耦合计算的研究可以分为两大类:一类侧重于构建精度较高的霍尔电场求解方法[11-13];另一类侧重于分析霍尔效应对磁控系统的影响效果[10,14-15]。
尽管上述研究大都实现了流场和霍尔电场的耦合计算,但现有方法对于拓扑结构复杂、网格规律大的流体域耦合计算的效率仍较低。因此,非平衡流场和电场耦合计算效率还需仔细研究。在该松耦合过程中有两个重要的控制参数,一是电场更新间隔S,即非平衡流场计算S时间步电场开始并完成一次迭代;二是电势残差收敛极限ε,即当电势残差小于该值时判定电场收敛。不同霍尔系数下电场的收敛性差别较大,给两参数取值带来困难。文献[16]采用的电场更新间隔在10~100之间,具体数值取决于算例的磁场强度。文献[17]在进行参数霍尔效应研究时,对于不同的霍尔系数采用了同样的电场更新间隔(S=200)和同样的电势收敛极限(ε=1×10-4)。可见,现有文献尚未考虑不同霍尔系数下电场收敛性对耦合效率的影响,也并未确定不同霍尔系数下电场更新间隔和收敛极限的合理取值方法。本文将首先建立三维热化学非平衡流场和霍尔电场的数值方法以及流场-电磁场之间的耦合计算方法,而后分析在不同霍尔系数下电场更新间隔和收敛极限对耦合计算效率的影响,以便为高超声速飞行器前缘磁控热防护系统的霍尔效应研究提供参考。
1 数学模型
1.1 控制方程
针对高超声速飞行器前缘流动特点,电磁场和流场耦合分析采用低磁雷诺数假设下的三维热化学非平衡磁流体(Magnetohydrodynamic,MHD)控制方程,如式(1)所示。其中,热化学非平衡模型采用Park双温度模型,化学反应动力学模型采用11组元20反应的Gupta模型。
(1)
式中:U为守恒变量,F、G、H分别为x、y、z方向的对流通量矢量,Fv、Gv、Hv为三方向上的黏性通量项,W为化学反应和振动能量源项矢量,具体表达式见文献[18]。相对于热化学非平衡黏流,上述方程增加了一个电磁源项通量SMFD,见下式
SMFD=
(2)
式中:J=(Jx,Jy,Jz)为电流密度矢量,E为电场强度矢量,B=(Bx,By,Bz)为磁感应强度矢量。γ表征不同非平衡模式间的电磁能量分配比,介于0和1之间,这里取γ=0.5[13]。磁感应强度B在给定磁场形态后即可确定,这里采用磁偶极子磁场[14]。考虑霍尔效应后,结合低磁雷诺数假设可以将对感应场强矢量E的求解转化为对标量电势φ的求解。由广义欧姆定律(3)和电流守恒方程(4)
(3)
▽·J=0
(4)
可以得到关于φ的电势泊松方程

(5)
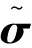
(6)
式中:B为磁感应强度矢量B的模。σ为标量电导率,采用式(7)非平衡流电导率模型进行计算。β为霍尔系数。为全面分析不同霍尔系数下耦合效率,采用两种方法确定β:1)式(7)非平衡模型[14];2)均匀分布。
(7)
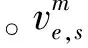
1.2 数值方法
磁流体流动方程(1)离散时,对流项差分采用基于MUSCL插值的AUSMPW格式,隐式求解采用了LU-SGS格式,并且对化学反应、振动以及电磁源项采用了隐式处理以削弱源项过大带来的刚性从而提高收敛性。
电势泊松方程(5)的离散基于单元中心有限体积法。采用交替隐式近似因子分解法(ADI-AF),转化为下式迭代求解
(8)
其中,系数a1i-1,b1i,c1i+1如下所示
(9)
此外,a2j-1,b2j,c2j+1,a3k-1,b3k,c3k+1形式类似,不再赘述。其中,
(10)
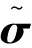
2 耦合方法与边界条件
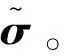
流场边界条件:流动入口为自由来流;出口采用超声速外推条件;壁面采用全催化等温壁,壁温取决于试验工况。霍尔电场边界条件:绝缘壁面,J·n=0; 导电壁面,φ=0 V; 其余边界为Neumann边界,▽φ·n=0。
3 仿真校验
3.1 霍尔电场校验
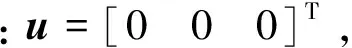
算例2为间隔电极霍尔效应算例,如图3所示[13]。±y的通道边界内通入+x向的导电流体,电导率σ=1Ω-1m-1。有限宽度的平行电极沿周期性重复布置在通道两侧壁面上。由于通道无限长,图中的进口和出口边界设置为周期性边界。为使通道内流体速度场对电势场结果无影响,则必须满足▽×(u×B)=0,因此可假定u=f(y),B=f(z),且通道内流动为充分发展的Poiseuille流动。其中,通道中心线上的流体速度umax=1m/s,通道半宽h=0.5m。
当B=0 T时,两电极间只存在静电场。图4为无霍尔效应时的本文和文献[13]的电势等值线对比图。图5为有霍尔效应时(β=1.0、B=1T)时的本文与文献的电流流线对比图。从图4~5可以看出,两种情况下,本文计算结果与文献结果吻合良好。
3.2 磁流体气动热校验
气动热模拟的准确性是检验耦合非平衡磁流体计算方法正确性的重要标准。选用日本1996年发射的轨道再入试验飞行器(Orbital reentry experiment, OREX)返回舱前体作为计算模型,如图6所示。选取再入飞行时间在7471.5s(Ma=17.61、H=59.6km)的飞行工况,并采用了有限催化壁面模型(γ=5.0×10-3)进行了气动热数值模拟。图7分别给出了三种外加磁场情况(B0=0.0、0.3、0.5 T)下的平动温度和壁面热流分布。通过与Fujino等[20]计算结果的比较可以看出,本文的激波脱体距离、壁面热流计算结果和文献[20]吻合良好。验证了本文外加磁场作用下的非平衡流场及气动热数值模拟的准确性。值得一提的是,图7(a)中平动温度峰值的差异以及图7(b)中当B0=0.3 T时在y/L=1.3(L为参考长度,L=1.0139m)附近的壁面热流差异,可能与本文和文献采用了不同的平动-振动松弛模型有关。
4 计算工况
为了提高耦合计算效率,需要确定电磁场参数相对于流动参数的最优的更新方式,即研究电场更新间隔S、电场残差收敛极限ε对耦合计算效率的影响。其中耦合计算效率以平均单步迭代时间ta,总收敛时长tc表示。
计算模型网格和第2.2节相同。采用OREX飞行器7461.5s飞行工况(Ma=20.04,H=63.60km)。驻点磁感应强度B0=0.2 T。流场计算采用当地时间步长,库朗特数取0.2。鉴于霍尔系数不同对电场收敛性影响巨大,从而会对耦合计算效率产生重要影响。这里根据霍尔系数不同设计了两组算例:1)均布霍尔系数β=1.0,步进因子ap=0.002;2)Fujino霍尔系数模型,步进因子ap=0.006。前者霍尔系数相对较小,电场收敛快;后者霍尔系数相对较大(β≈5.0~10.0),电场收敛较慢。耦合计算以忽略霍尔效应的流场收敛解作为初场。
5 结果与分析
表1给出了均布霍尔系数β=1.0时不同电场更新间隔下的单步平均迭代时间和收敛时的总迭代时间。从表1可以看出,和S=10相比,电场更新间隔S≥100时,单步迭代时间和收敛总时间大幅减小,而后随着电场更新间隔的增加,单步平均迭代时间和收敛总时间虽略微减少但整体变化不大。导电壁面和绝缘壁面规律一致。

表1 不同电场更新间隔下的迭代时间对比Table 1 Iteration time under different updating intervals of electric field (β=1.0)
图8(a)和(b)分别为导电壁面不同电场更新间隔下流场和电场的收敛曲线。从图8可以看出,电场更新间隔对流场收敛曲线形状影响较小,随电场更新间隔的增加收敛步数略微减少。电场更新间隔对电势场收敛影响较大,并且电场更新间隔越大,相同电场迭代步数流场收敛程序越高,相应的电势收敛所需的电场虚拟时间步越少。
表2给出了采用非平衡霍尔系数模型时不同电场更新间隔下的单步平均迭代时间和收敛总时间。表2还对比了两种电势收敛残差极限下的结果。可以看出,电势残差收敛极限为10-4时,电场收敛耗时较多,单步平均迭代时间较长(S=10时约为58s),耦合计算时间呈现先降后升的趋势,最优的电场更新间隔为1000。而当电势残差收敛极限为10-3时,在S=10~5000范围内,电场更新间隔越大,单步平均迭代时间和总收敛时间越小,同β=1.0时规律一致。另外,当S=1000时,两个收敛极限(ε=10-3、10-4)下的总收敛时间相近,但电场间隔越小二者收敛时间相差越大,S=10时总收敛时间10-4可达10-3的110倍,此时采用相对较大的收敛残差极限(10-3)可以极大地提高耦合计算效率。

表2 不同电场更新间隔下的迭代时间对比Table 2 Iteration time under different updating intervals of electric field (nonequilibrium Hall parameter model)
5 结 论
以高速飞行器磁控热防护系统为研究对象,针对其在真实气体条件下高温流场和电磁场的耦合求解问题,建立了非平衡流场、外加磁场和霍尔电场的松耦合计算方法,在此基础上分析了耦合计算效率与电场更新间隔、电势残差收敛极限的关系。研究表明,霍尔系数较小(β=1.0)时,电场更新间隔S=100相比S=10单步迭代时间和收敛总时间大幅减少。S>100后随电场更新间隔的增加略微减少,计算效率变化不大,并且导电壁面和绝缘壁面规律一致。霍尔系数较大时,电场收敛缓慢,耦合计算时间过长,可以通过适当增加电场迭代间隔以及提高电势收敛极限的方法有效提高耦合计算效率。采用霍尔系数非平衡模型时,电场更新间隔的建议取值为1000,电势收敛极限可取10-3。
[1] 孟松鹤,杨强,霍施宇,等. 一体化热防护技术现状和发展趋势[J]. 宇航学报, 2013, 34(10): 1295-1302. [Meng Song-he, Yang Qiang, Huo Shi-yu, et al. State of arts and trend of integrated thermal protection systems [J]. Journal of Astronautics, 2013, 34(10): 1295-1302.]
[2] 李锋,艾邦成,姜贵庆. 一种热平衡等温机制的新型热防护及相关技术[J]. 宇航学报, 2013, 34(12): 1644-1650. [Li Feng, Ai Bang-cheng, Jiang Gui-qing. A new thermal protection technology based on heat balance isothermal mechanism [J]. Journal of Astronautics, 2013, 34(12): 1644-1650.]
[3] 潘勇,王江峰,伍贻兆. 非结构网格高超声速MHD流场逆风格式数值模拟[J]. 宇航学报, 2008, 29(1): 104-109. [Pan Yong, Wang Jiang-feng, Wu Yi-zhao. Numerical simulation of hypersonic MHD flows using upwind scheme on unstructured grids [J]. Journal of Astronautics, 2008, 29(1): 104-109.]
[4] 张康平,丁国昊,田正雨,等.磁流体动力学控制二维扩压器流场数值模拟研究[J].国防科技大学学报, 2009, 31(6):39-41. [Zhang Kang-ping, Ding Guo-hao, Tian Zheng-yu, et al. Numerical simulation of magnetohydrodynamic (MHD) control on 2D diffuser′s flow field [J]. Journal of National University of Defense Technology, 2009, 31(6):39-41.]
[5] 田正雨,张康平,潘沙,等.磁流体动力学斜激波控制数值模拟分析[J]. 力学季刊, 2008, 29(1):72-77. [Tian Zheng-yu, Zhang Kang-ping, Pan Sha, et al. Numerical investigation and analysis for MHD oblique shock control[J]. Chinese Quarterly of Mechanics, 2008, 29(1):72-77. ]
[6] Bityurin V A, Bocharov A N. Study of catalytic effects at reentry vehicle [C].The 52nd Aerospace Sciences Meeting, National Harbor, Maryland, USA, January 13-17, 2014.
[7] Cristofolini A, Borghi C A, Neretti G, et al. MHD interaction around a blunt body in a hypersonic unseeded air flow[C].The 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, September 24-28, 2012.
[8] 刘深深,桂业伟,唐伟,等.一种多场耦合数据传递新方法[J]. 宇航学报, 2016, 37(1):61-67. [Liu Shen-shen, Gui Ye-wei, Tang Wei, et al. A new data transfer method in fluid-thermal-structrure coupling problems [J]. Journal of Astronautics, 2016, 37(1): 61-67.]
[9] 吕浩宇, 李椿萱.Hall效应对磁流体压缩管道电磁流动特性的影响[J].科学通报, 2010, 55(12):1182-1188. [Lv Hao-yu, Li Chun-xuan. Influence of Hall effects on characteristics of magnetohydrodynamic converging channel [J]. Chin. Sci. Bull, 2010, 55(12):1182-1188.]
[10] 胡海洋, 杨云军, 周伟江. 大霍尔系数下电离气体与磁场相互作用规律数值研究[J]. 力学学报,2011, 43(3): 453-460. [Hu Hai-yang, Yang Yun-jun, Zhou Wei-jiang. Numerical research on the interaction between ionized gas and magnetic field under high Hall parameter [J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3):453-460.]
[11] Gaitonde D V, Poggie J. Elements of a numerical procedure for 3-D MGD flow control analysis [C]. 40th AIAA Aerospace Sciences Meeting and Exhibit, Reno, USA, January 14-17, 2002.
[12] Wan T, Candler G V, Macheret S O, et al. Three-dimensional simulation of the electric field and magnetohydrodynamic power generation during reentry [J]. AIAA Journal, 2009, 47(6):1327-1336.
[13] Bisek N J. Numerical study of plasma-assisted aerodynamic control for hypersonic vehicles [D]. Michigan: The University of Michigan, 2010.
[14] Fujino T, Matsumoto Y, Kasahara J, et al. Numerical studies of magnetohydrodynamic flow control considering real wall electrical conductivity [J]. Journal of Spacecraft and Rockets, 2007, 44(3):625-632.
[15] 吕浩宇,李椿萱,董海涛. 三维超声速磁流体发生器的流动特性[J]. 中国科学G辑,2009,39(3):435-445. [Lv Hao-yu, Li Chun-xuan, Dong Hai-tao. Characterization of the three-dimensional supersonic flow for the MHD generator [J]. Science in China Series G-Physics Mechan. Astron. , 2009, 39(3):435-445.]
[16] Bisek N J, Gosse R, Poggie J. Computational study of impregnated ablator for improved magnetohydrodynamic heat shield [J]. Journal of Spacecraft and Rockets, 2013, 50(5): 927-935.
[17] Otsu H, Konigorski D, Abe T. Influence of Hall effect on electrodynamic heat shield system for reentry vehicles [J]. AIAA Journal, 2010, 48(10):2177-2186.
[18] 柳军.热化学非平衡流及其辐射现象的实验和数值计算研究[D].长沙:国防科技大学,2004. [Liu Jun. Experimental and numerical research on thermo-chemical nonequilibrium flow with radiation phenomenon [D]. Changsha: National University of Defense Technology, 2004.]
[19] Gnoffo P A, Gupta R N, Shinn J L. Conservation equations and physical models for hypersonic air flows in thermal and chemical nonequilibrium [R]. NASA, TP-2867, 1989.
[20] Fujino T, Ishikawa M. Numerical simulation of control of plasma flow with magnetic field for thermal protection in earth reentry flight [J]. IEEE Transactions on Plasma Science, 2006,34(2):409-420.
通信地址:湖南省长沙市国防科技大学航天科学与工程学院(410073)
电话:15616246843
E-mail:likai898989@126.com
(编辑:牛苗苗)
Numerical Methods of Coupling High Temperature Flow Field with Electro Magnetic Field for Magnetohydrodynamic Heat Shield System
LI Kai, LIU Jun, LIU Wei-qiang
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
Under the real flight conditions, the Hall effect usually cannot be neglected which may affect the performance of the magnetohydrodynamics(MHD) thermal protection. Therefore, the coupled numerical simulations are conducted for the thermochemical nonequilibrium flow field, the externally applied magnetic field and the induced electric field around a typical hypersonic vehicle. After that, the relations between the coupled calculation efficiency and the updating interval of the electric field as well as the converging residual limit of the electric potential are analyzed. Results show that the coupled calculation efficiency is higher under the condition that the updating interval is greater than 100 flow steps during a relatively smaller Hall parameter. However, during a larger Hall parameter, the coupling efficiency is lower but can be improved by increasing the updating interval of the electric field and potential residual limit. The suggested updating interval and potential residual limit are also given while the nonequilibrium Hall parameter model is utilized.
MHD flow control; Thermal protection; Hall electric field; Coupled computation
2016-09-26;
2017-02-27
国家自然科学基金(90916018);湖南省自然科学基金重点资助项目(13JJ2002)
V211.1
A
1000-1328(2017)05-0474-07
10.3873/j.issn.1000-1328.2017.05.005
李 开(1989-),男,博士生,主要从事磁流体流动控制,高温气体动力学以及飞行器热防护系统设计方面的研究。

