火星EDL过程动力学建模与仿真

张青斌, 丰志伟, 马 洋, 葛健全, 高兴龙, 高庆玉

(1. 国防科学技术大学航天科学与工程学院，长沙 410073；2. 火箭军工程大学，西安 710025；3. 中国空气动力研究与发展中心设备设计及测试技术研究所，绵阳 612000)

火星EDL过程动力学建模与仿真

张青斌1, 丰志伟1, 马 洋2, 葛健全1, 高兴龙3, 高庆玉1

(1. 国防科学技术大学航天科学与工程学院，长沙 410073；2. 火箭军工程大学，西安 710025；3. 中国空气动力研究与发展中心设备设计及测试技术研究所，绵阳 612000)

针对火星着陆器的进入、减速和着陆(EDL)过程的关键动力学问题，分别建立着陆器进入、降落伞拉直、充气和稳定着陆等各阶段的较精细的动力学模型，并构建初步的多学科集成分析框架。基于着陆器六自由度刚体模型，仿真研究火星进入弹道的动力学特性；采用过载上升段自适应控制开伞策略，确定降落伞的开伞条件；利用降落伞拉直充气经验模型以及九自由度物-伞多体系统模型，研究降落伞减速过程的动力学特性；采用面向对象设计语言，建立EDL多学科集成仿真框架，从而实现火星着陆器从进入点至着陆点EDL全过程的参数化建模。本文所建模型可有效预测火星EDL过程的运动特性，也可指导深空探测中EDL系统的分析设计。

火星探测；降落伞动力学；气动减速；集成仿真

0 引 言

火星着陆器的进入、减速和着陆(Entry, descent, and landing，EDL)技术是火星探测实施过程的关键技术之一[1]。火星着陆器在火星表面实现软着陆的过程与地球上着陆过程类似：着陆器在进入大气层之后，首先通过着陆舱的气动外形减速，而后将弹出降落伞，进一步减速；然后，在接近地面时，采用制动火箭发动机的反推作用再度减速，并通过气囊或者着陆支架的方式进行着陆缓冲，最后实现着陆器软着陆。目前，美、俄实现火星着陆也是采用这种方法进行设计。火星进入过程由于环境和飞行状态变化剧烈，火星再入参数的选择和轨迹控制直接影响到开伞条件和着陆精度[2-3]。由于火星和地球的环境存在较大差异，并且火星环境的许多参数具有很大的不确定性，因而研究EDL的高精度动力学模型以及相应的偏差分析具有重要的工程应用价值。

国内外学者针对火星探测的任务需要，进行大量的动力学研究工作。Braun[4]基于“火星探路者”(Mars Pathfinder，MPF)建立了六自由度的进入弹道模型，对MPF的进入弹道进行了分析。Spencer等[5]以MPF为研究对象，对火星大气的进入轨迹设计以及误差分析进行了研究。Desai等[6]建立了MER火星探测器的六自由度进入弹道模型，并对MER的进入弹道的动力学特性进行了分析。在多次火星探测任务的基础之上，美国已建立了POST2、DSENDS和其他相关专业仿真工具，也对火星EDL过程进行了大量的仿真分析[7-9]。陈阳等[10]利用火星着陆器进入段的三自由度模型，分析着陆器的飞行性能，研究火星进入点误差对开伞点分布的影响。张青斌[11]和Gao等[12-13]建立了降落伞回收过程中拉直、充气及稳定下落各阶段的动力学模型，开展了大量研究工作，最近几年也研究了火星环境下降落伞相关动力学问题[14]。

尽管深空探测技术受到越来越多的关注，但是我国在火星EDL全过程的分析设计研究方面与美国还存在一定差距。虽然对EDL各个阶段和关键技术进行了相关研究[15]，包括开伞控制技术[16]，拉直过程动力学建模[17]，降落伞充气[18]等，但是缺乏完整的集成仿真程序来进行火星EDL过程的全弹道特性分析。本文采用火星着陆器六自由度刚度动力学模型，以及降落伞减速阶段的九自由度动力学模型，结合火星环境模型和气动数据，分析了火星探测器从进入直到落地的动力学特性；最后建立了火星EDL动力学集成仿真框架，并实现了EDL过程的降落伞开伞及弹道数据的三维视景显示。

1 气动特性分析

为了便于搭建EDL多学科集成分析框架，本文采用ANSYS Fluent商业软件进行火星探测器和降落伞绕流流场的计算。选取k-ε两方程湍流模型，并配合使用非平衡壁面函数，这样更适合于模拟流场中出现的大分离和大漩涡特性；对流项离散采用二阶AUSM格式；探测器和降落伞表面满足无滑移边界条件。按照稀薄气体动力学理论，采用Knudsen数Kn来衡量流动的连续性，即

Kn=λ/L

(1)

式中：λ为分子的平均自由程，L为流动的特征长度，本文取探测器的最大直径。

文献[14]将Kn数与流动计算中熟知的马赫数Ma和雷诺数Re联系起来，得到如下关系：

(2)

式中：γ为气体的比热比，火星大气取1.3。

将式(2)进一步整理得：

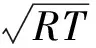
(3)

式中：μ为气体黏性系数，只与气体温度T有关。R为气体常数。p和T分别为气体的压力与温度。由式(3)可知，流动的Kn数只与气体的状态参数和特征长度相关。将火星大气对应的参数代入式(3)，计算得到Kn数约为1.5×10-6，远小于需要考虑稀薄气体效应的临界Kn数(0.01)，因此本文所有涉及的流动满足连续介质假设。

本文对比分析了亚、跨和超声速4个马赫数、0～30°的5个攻角以及两种大气环境条件下的探测器的气动性能。图1给出了探测器气动特性随攻角的变化情况，其中实线和虚线分别表示火星大气环境和地球大气环境下气动特性；正方形、三角形和圆圈标记分别表示亚、跨、超声速情况下的气动特性。所有气动力系数都以火星大气环境参数为参考值。仿真结果表明，在0～30°攻角范围内探测器气动特性的线性度都较好。随着攻角的增大，探测器的升力系数CL、阻力系数CD都变小。

2 火星大气环境模型

本文在探测器进入弹道和降落伞减速过程动力学研究时，采用火星全球参考大气模型(Mars global reference atmosphere model, Mars-GRAM)，并以Mars-GRAM 2005为基准模型，重构火星大气模型，利用其数据进行最小二乘拟合可以得到火星大气密度、压力与高度的一个拟合关系如下[19]

(4)

式中：h为着陆器到火星表面的距离，单位为km；T为火星大气温度，单位为K；p为大气压力，单位为N/m2；ρ为大气密度，单位为kg/m3。

3 轨迹动力学

本文根据探测任务将着陆器再入火星大气层至着陆的整个EDL过程大体划分为6个阶段：着陆器自身气动外形减速阶段、降落伞弹射拉直阶段、降落伞充气展开阶段、降落伞全张满减速阶段、抛防热大底阶段、脱降落伞后降落伞-背罩组合体下降阶段，如图2所示。

3.1 再入动力学

本文采用六自由度刚体模型研究火星进入段的弹道特性，标量形式的动力学方程如下

(5)

(6)

式中：r是地心距，φ是纬度，V是速度大小，θ是俯仰角，ψ是偏航角，γ是滚转角，ωM是火星自转角速度(7.088×10-5rad/s)，g是其重力加速度，ωx、ωy和ωz为体角速度,将着陆器简化为轴对称质量分布，Jx、Jy和Jz为转动惯量分量,Mx、My和Mz为着陆器所受到合力矩分量。

3.2 物-伞动力学

本文分别采用理想拉直过程动力学、充气过程经验公式和物-伞多体系统动力学模型，研究降落伞减速过程的动力学特性。

3.2.1 拉直充气阶段

EDL过程的集成分析模型，采用Wolf理想情况下直线拉出模型模拟降落伞拉直的变质量动力学过程[20]。模型假设为：伞绳及伞衣按序从伞包内拉出，且在拉直过程中回收物和引导伞在每一瞬时遵循相同的弹道倾角[11]。同时建立可反映“绳帆”现象的多体动力学模型。降落伞充气过程的主要参数为伞衣阻力面积变化，在仿真计算中，采用的经验公式描述开伞过程中参考面积变化规律[21]

(7)

式中：t为飞行时间，tf为盘缝带伞开伞时间，kf为修正系数。

3.2.2 稳定下落过程

为便于计算，对火星所用盘缝带伞-着陆器系统的简化假设如下：

1)降落伞是轴对称的，伞衣完全充满后具有固定形状，而降落伞与着陆器以球铰相连，系统为二刚体。

2)由于降落伞运动的非定常性引起的气动力或力矩的增量部分用附加质量和附加质量惯性矩来表示。

3)忽略着陆器尾流对降落伞的影响。

在盘缝带伞-着陆器九自由度动力学模型中，需要建立大地固连坐标系、以及着陆器和盘缝带伞上的固连坐标系，如图3所示[22]：大地固连坐标系Od-XdYdZd原点Od取为盘缝带伞-着陆器系统投放瞬间着陆器在地面的投影点处，OdXd轴沿着重力方向铅垂向下，OdYd轴、OdZd轴与OdXd轴构成右手直角系;伞体坐标系O-XpYpZp原点O取在铰接点处，OXp轴沿着盘缝带伞的对称轴向下，轴OYp和轴OZp符合右手法则;着陆器体坐标系O-XbYbZb原点O取在铰接点处，OXb轴沿着着陆器的对称轴指向下，轴OYb、轴OZb符合右手法则。

盘缝带伞质量及附加质量记为矩阵mp，其对铰接点O的转动惯量则以矩阵Ip表示，着陆器的质量以mb表示，其对铰接点O的转动惯量则以矩阵Ib表示。盘缝带伞广义质量和惯量的表达式如下：

(8)

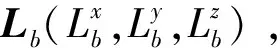
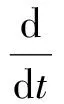
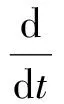
(10)

(11)

综合式(9)～(11)可进行仿真分析盘缝带伞-着陆器系统的动力学特性，获得物-伞系统稳定下落阶段的弹道特性[23]。

4 初始条件与开伞控制策略

4.1 初始条件与开伞控制策略

开伞控制是着陆系统进行气动减速的第一步，也直接关系到降落伞工作的成败，确定合适的开伞点是火星再入弹道中的关键技术。本文针对火星进入的特点，应用作者在文献[19]中提出的自适应过载开伞控制策略。对于弹道式火星进入，过载曲线有一个非常典型的形状，根据过载曲线上升段特性与控制马赫数(或动压)的数据信息建立数学关系，形成过载上升段自适应开伞控制方法。基于上文气动模型以及火星大气环境模型，采用六自由度再入弹道模型进行仿真计算，其标称弹道的仿真初始条件如表1所示。利用自适应过载开伞控制方法，以控制马赫数1.8为例选择的开伞点作为降落伞稳定下落阶段仿真的初始条件，其它初始参数如表2所示。

表2 过载上升段自适应开伞控制初始条件Table 2 Initial conditions of the adaptive parachute opening control method

4.2 EDL全弹道仿真

利用上文所建立的九自由度动力学模型，通过给定的初始条件可以进行全过程的弹道仿真，获得动力学特性。其中图4为高度时间曲线，图5为速度时间曲线，图6为高度速度曲线，图7为过载时间曲线、图8为动压时间曲线、图9为马赫数时间曲线，上述图中实线为进入弹道、虚线为降落伞减速过程、黑点为开伞点。上述仿真结果与文献[4]一致，说明了本文动力学模型的有效性。

4.3 集成仿真框架

火星探测器降落伞分系统的设计涉及到EDL过程的各个阶段，参数较多且对着陆性能存在不同程度的影响。其中降落伞减速阶段是分系统的关键工作阶段，对着陆成败影响较大。为了分析这些参数对着陆性能的影响，并为进一步实现EDL全过程弹道的优化设计奠定基础，需要建立EDL系统动力学集成仿真框架(包括火星再入动力学、伞包弹射动力学、降落伞拉直动力学、降落伞充气动力学、充满稳定下落动力学等动力学仿真模块)，通过计算机程序指令将各分系统的仿真模块进行串联集成并自动运行，以提高设计的效率并寻得较优化的方案或参数组合。该软件需要通过选择行星模型和进入方案，输入进入体的尺寸参数和工况参数、降落伞的尺寸参数、工况参数和材料参数、再入点参数、大气环境参数和气动力系数偏差等。图10为火星盘缝带伞-着陆器系统的设计界面。以给定的火星探测任务为例，通过给定的初始条件进行仿真，得到相应的开伞过程和弹道性能参数的显示结果，如图11所示。

5 结 论

本文针对火星探测中EDL过程的动力学问题，分别采用火星着陆器六自由度动力学模型，以及降落伞减速阶段的九自由度动力学模型，结合火星环境模型并采用ANSYS Fluent商业软件进行火星探测器和降落伞绕流流场的计算，仿真分析火星探测器从进入直到落地的动力学特性；同时也融合自适应开伞控制方法，建立火星EDL动力学多学科集成仿真框架，将盘缝带伞拉直充气过程动力学模型一同集成到该框架下，最终获得较完整的火星弹道的参数化建模与仿真分析。本文的研究成果可以指导深空探测中降落伞减速弹道的分析设计。

[1] Braun R D, Manning R M. Mars exploration entry, descent, and landing challenges [J]. Journal of Spacecraft and Rockets, 2007, 44(2): 310-323.

[2] Cruz J R. Parachute models used in the Mars science laboratory entry, descent, and landing simulation [C].AIAA Aerodynamic Decelerator Systems,Daytona Beach, USA, March 25-28, 2013.

[3] Ren G. A rapid uncertainty propagation method for pre-parachute phase of Mars entry [R]. Chinese Control and Decision Conference(CCDC), 2011: 3142-3147.

[4] Braun R D. Mars Pathfinder six-degree-of-freedom entry analysis [J]. Journal of Spacecraft and Rockets, 1995, 32(6): 993-1000.

[5] Spencer D A, Braun R D. Mars Pathfinder atmospheric entry: trajectory design and dispersion analysis [J]. Journal of Spacecraft and Rockets, 2015, 33(5): 670-676.

[6] Desai P N, Schoenenberger M, Cheatwood F M. Mars exploration rover six-degree-of-freedom entry trajectory analysis [J]. Journal of Spacecraft and Rockets, 2006, 43(5): 1019-1025.

[7] Raiszadeh B. POST II trajectory animation tool using MATLAB, V1.0. 2005[R]. Hampton, USA: Langley Research Center, July 2005.

[8] Robin M. Navigation flight operations for mars pathfinder [J]. Journal of Spacecraft & Rockets, 1998, 36(3): 340-347.

[9] Austin R. DSENDS-A high-fidelity dynamics and spacecraft simulator for entry, descent and surface landing[C]. IEEE, Aerospace Conference, Montana, USA, March 9-16,2002.

[10] 陈阳, 孙海滨, 郭雷. 火星进入点误差对开伞点分布影响分析[J]. 中国空间科学技术, 2014(3): 73-78. [Chen Yang, Sun Hai-bin, Guo Lei. Analysis of parachute deployment deviation for Mars entry under initial condition errors [J]. Chinese Space Science and Technology, 2014(3): 73-78.]

[11] 张青斌. 载人飞船降落伞回收系统动力学研究 [D].长沙：国防科学技术大学，2003. [Zhang Qing-bin, Dynamic research on system[D]. Changsha: National University of Defense Technology, 2003.]

[12] Gao X L, Zhang Q B, Tang Q G, Parachute dynamics and perturbation analysis of precision airdrop system [J]. Chinese Journal of Aeronautics, 2016, 29(3): 596-607.

[13] Gao X L, Zhang Q B, Tang Q G. Transient dynamic modeling and analysis of complex parachute inflation with fixed payload [J]. Journal of Aerospace Engineering, 2015(28): 04014097.

[14] Gao X L, Zhang Q B, Tang Q G. Numerical modeling of Mars supersonic disk-gap-band parachute inflation [J]. Advances in Space Research, 2016.

[15] 荣伟, 鲁媛媛，包进进, 等. 火星探测器减速着陆过程中若干问题的研究 [J]. 南京航空航天大学学报, 2016, 48(4): 445-453. [Rong Wei, Lu Yuan-yuan, Bao Jin-jin, et al. Several problems relative with descent and landing process of Mars explorer [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(4): 445-453.]

[16] 荣伟, 陈旭, 陈国良. 火星探测着陆系统开伞控制方法研究 [J]. 航天返回与遥感, 2007, 28(4): 6-11. [Rong Wei, Chen Xu, Chen Guo-liang. The control method study on the parachute deployment for the Mars exploration landing system [J]. Spacecraft Recovery & Remote Sensing, 2007, 28(4): 6-11.]

[17] 鲁媛媛, 荣伟, 吴世通, 火星环境下降落伞拉直过程的动力学建模 [J]. 航天返回与遥感, 2014, 35(1): 29-36. [Lu Yuan-yuan, Rong Wei, Wu Shi-tong. Dynamic modeling of parachute deployment in Mars environment [J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 29-36.]

[18] 高兴龙, 张青斌，丰志伟, 等. 集成火星进入弹道的开伞过程动力学特性研究 [J]. 宇航学报, 2016, 37(6): 664-670. [Gao Xing-long, Zhang Qing-bin, Feng Zhi-wei, et al. Study on dynamic characteristic of opening process integrating with Mars entry trajectory [J]. Journal of Astronautics, 2016, 37(6): 664-670.]

[19] 王慧娟. 火星着陆器进入与降落伞减速动力学研究[D]. 长沙: 国防科技大学, 2015. [Wang Hui-juan. Research on Mars lander and parachute decelerating dynamics[D]. Changsha: National University of Defense Technology, 2015.]

[20] Wolf D. A simplified dynamics model of parachute inflation [R]. AIAA 4th Aerodynamics Deceleration Systems Conference, Palm Springs, California, 1973: 1-9.

[21] 唐乾刚，张青斌，张晓今, 等. 伞-弹系统九自由度动力学模型 [J]. 兵工学报, 2007, 28(4): 449-452. [Tang Qian-gang, Zhang Qing-bin, Zhang Xiao-jin, et al. Nine-degree-of-freedom model of bomb-parachute system [J]. ACTA ARMAMENTARII, 2007, 28(4): 449-452.]

通信地址：长沙国防科学技术大学航天科学与工程学院(410073)

电话：(0731)84576436

E-mail:qingbinzhang@sina.com

(编辑：牛苗苗)

Modeling and Simulation of Mars EDL Process

ZHANG Qing-bin1, FENG Zhi-wei1, MA Yang2, GE Jian-quan1, GAO Xing-long3, GAO Qing-yu1

(1.College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China; 2. Rocket Force University of Engineering, Xi’an 710025, China; 3. Facility Design and Instrumentation Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China)

Focusing on the key dynamic problems of a Mars probe in the entry, descent and landing (EDL) stages, the detailed dynamic models including the entry of the probe, the deployment, inflation, and steady descent for the parachute are built. The dynamic characteristics of the Mars entry trajectory are analyzed based on the 6-DOF model, the initial simulation conditions of the parachute deceleration are achieved by the ascendant adaptive opening control method, and the dynamic characteristics of the parachute′s deceleration are investigated by the empirical models of the parachute′s deployment and inflation and the 9-DOF multi-body model of the parachute-body. Finally, an integration simulation framework of the EDL is established based on the object oriented design language, achieving parametric modeling of the EDL whole process from the Mars entry point to landing point. The results of this paper could be applied to effectively predict the dynamics of the Mars EDL process, and guide the integration design analysis of a Mars landing system.

Mars exploration; Parachute dynamics; Aerodynamic deceleration; Integration simulation

2016-04-18;

2017-03-22

国家自然科学基金(5137548611)

V11

A

1000-1328(2017)05-0443-08

10.3873/j.issn.1000-1328.2017.05.001

张青斌(1975-)，男，博士，副教授，主要从事物-伞多体系统动力学、飞行器总体多目标优化等方面的研究。