定平面形状乘波体及设计变量影响分析
刘传振,白 鹏,陈冰雁,周伟江
(中国航天空气动力技术研究院,北京100074)
定平面形状乘波体及设计变量影响分析
刘传振,白 鹏,陈冰雁,周伟江
(中国航天空气动力技术研究院,北京100074)
拓展密切锥方法的设计灵活性,提出了一种定平面形状乘波体概念。推导了设计参数与平面形状之间的泛化几何关系,使用非均匀有理B样条辅助设计,建立了头部区域可控、后掠区域可控的双后掠乘波体设计方法,并给出了此类乘波体外形参数与设计参数之间的几何关系。结合考虑黏性的乘波体性能快速预估方法评估乘波体性能,并通过CFD技术验证了设计和性能评估方法的有效性。提取设计变量,分析典型变量对乘波体性能的影响。结果表明,双后掠乘波体保持了高超声速阶段的高升阻比特性,同时具有对平面形状良好的可控性,为构建新型乘波体外形提供了思路。
乘波体;定平面;双后掠;设计变量;气动性能
0 引 言
近年来,具有高升阻比特性的乘波体成为了国际研究的重点和热点。Nonweiler[1]在1959年首先提出了乘波体设计理论,并通过楔形流场生成了‘Λ’型乘波体,Jones等[2]提出了使用轴对称锥形流动的锥导乘波体概念,增大了飞行器的容积,推动了乘波体飞行器的实用化。很多学者为扩大设计空间,发展使用了其他基准流场,包括带攻角的锥、椭圆锥流动[3]、一般三维流动[4-5]等。1990年,Sobieczky等[6]提出密切锥乘波体设计方法,通过给定激波形状拟合流场,可以生成具有更多特性的乘波体外形,灵活性很高。
但乘波体仍然有一些缺陷限制了它的工程应用,主要包括容积率不高,低速状态气动性能不好,纵向稳定性难以保证等。目前有一些解决方法,例如修改上表面外形扩充容积,串联不同展长的外形进行改善低速状态性能[7],改变基准流场部分提高纵向稳定性[8]等。这些方法具有较好的工程应用价值,但或是在外形生成之后进行修形,或难以提取设计参数进行控制,可控性不足。乘波体的曲面通过追踪流线得到,可修改性较低,而平面形状的设计自由度较高,因此控制平面形状生成乘波体外形是改善乘波体性能缺陷的新的思路。
对定平面形状乘波体有意义的探索是定后掠角乘波体,但在早期只是作为传统方法的附属。Starley等[9]提出了定常楔形角乘波体,因为采用了二维楔形流场,升阻比不高,体积利用率较低;Jones等[2]在介绍锥导乘波体时,提到过一种设计曲线过圆锥顶点的乘波体,但设计空间受限,方法不够灵活;最近几年,洛克希德马丁公司的Rodi[10]从密切锥乘波体设计方法出发,介绍了定后掠角密切锥和密切流场乘波体的概念;段焰辉等[11]给出了定后掠角乘波体具体实现,并提取设计变量进行了分析研究。
本文从定后掠角乘波体设计方法出发,推导了设计曲线与乘波体外形之间的全域性关系,对设计曲线进行拓展提出了定平面形状乘波体概念,重点研究了其中的双后掠外形。使用非均匀有理B样条(Non-uniform rational B-spline, NURBS)辅助设计,保证了双后掠乘波体曲面的连续光滑。使用CFD技术验证设计方法的有效性,并考察了设计变量对于双后掠乘波体性能的影响。
1 设计方法
1.1 两个重要的几何关系
密切锥乘波体设计方法可以由给定的激波形状拟合流场生成乘波体,设计方法中需要给出的设计曲线包括激波出口型线,也叫做进气捕获曲线(Inlet capture curve, ICC),和流线追踪的初始线-捕获流管(Flow capture tube, FCT)。在密切锥乘波体设计中,ICC曲线和FCT曲线的形状直接决定了乘波体的外形。本节讨论设计曲线与生成外形之间两个有用的几何关系,分别可以确定乘波体外形的平面形状和厚度分布。
图1给出了密切锥乘波体设计方法的局部示意图,作ICC曲线在G点的切线,过此点的垂面GH即为密切平面,密切平面内使用锥形流拟合,锥形流动有几个重要假设:1)激波平直,激波角为定值β;2)锥形流中所有的流线都是自相似的[12],可设定流线倾斜角等同于锥角γc。锥形流动一般采用数值方法求解Taylor-Macoll方程得到,尺度由ICC的当地曲率半径决定,如果ICC为直线,曲率半径无穷大,可使用二维楔形流动代替。H点为密切平面与FCT曲线的交点。ICC在G点斜率倾角为δ,FCT的斜率倾角为δ1,生成乘波体部分的长度为l,宽度为s。有关系式:
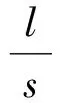
(1)
求解得到:
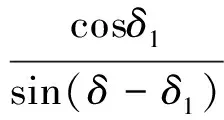
(2)
λ是当地前缘后掠角,在密切锥乘波体设计方法中,此条件全域性的,即使ICC和FCT曲线不为直线此公式也成立。
第二个关系是下表面偏转角关系,如图2所示,δ2为流线追踪法得到的乘波体下表面后缘(LS)在I点的斜率倾角。
有如下的关系:
(3)
得到
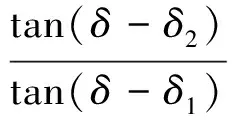
(4)
1.2 定平面形状乘波体设计
流场和激波的影响对乘波体性能更具决定性,在应用几何关系式时,简单起见,可以将FCT设定为水平直线,式(2)简化为文献[10]中提到的关系:
sinδ=tanλtanβ
(5)
根据式(5),当ICC存在斜率为0的直线时,对应乘波体外形部分后掠角为0,ICC存在为斜率不为0的直线时,对应外形为定后掠前缘,当ICC为一般曲线时,对应的外形的轮廓线为曲线,因此这个关系式允许我们通过给定ICC曲线的斜率和曲率定制乘波体的外形。图3给出了综合以上结论得到的平头前缘乘波体,通过ICC的斜率曲率可将乘波体分为平头部分,弯曲部分和后掠部分。
平头前缘乘波体有一定的研究意义,但更具有实用价值的是弯头或尖头外形。
如图4所示,去掉斜率为0的直线部分,ICC靠近对称轴部分设定圆弧段,直线段与圆弧不相切。一般取直线段倾角小于圆弧圆心角,否则导致乘波体曲面重叠。通过密切平面与FCT曲线的交点可以将FCT分为弯头区域、第一后掠区域和第二后掠区域,同时设定第一后掠区域的曲率由圆弧到直线逐渐过渡。所生成乘波体的平面形状类似双后掠布局,如图4所示。
图4所示的设计参数与乘波体平面形状控制参数之间存在对应的几何关系,设O点为坐标原点,圆弧半径为R,FCT偏移距离为r,圆弧圆心角为θ1,直线段倾角为θ2。计算乘波体的长度l,宽度s和弯头区域宽度sb:
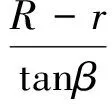
(6)
当r=0时,所生成的外形为尖头乘波体,当r=Rcosθ1时,此设计方法方法退化为FCT为水平直线的锥导乘波体。r不够直观,后文使用弯头度
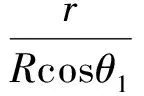
将其归一化。
第一和第二后掠区域的宽度s1,s2为:
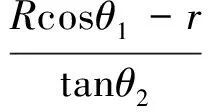
第一后掠区域前缘线不是严格意义的直线,可近似取T1T2两点的斜率角为第一后掠角λ1:
(7)
第二后掠角λ2可根据式(5)计算:
(8)
第二后掠区域的厚度分布角ε(与图2中的δ2对应)由式(4)求解:
(9)
根据式(6)~(9)即可通过弯头区域宽度、后掠角大小和厚度分布角求取r、β、θ1、θ2进行乘波体设计。
1.3 使用NURBS辅助设计
图4方法中,后掠区域的大小是固定的,难以控制;直线段斜率倾角与圆弧圆心角差距过大时,过渡点处斜率变化剧烈,可能影响下表面在对应位置的光滑分布。
为解决这些问题,本文引入非均匀有理B样条(Non-uniform rational B-spline, NURBS)表达ICC曲线辅助设计。分析图4中ICC曲线的构成,主要包括圆弧和直线部分。NURBS方法的最大优点之一就是能够精确的表示包括圆在内的圆锥截线[13],这一特性给了我们很大的便利进行密切锥的设计。p次NURBS曲线的定义为:
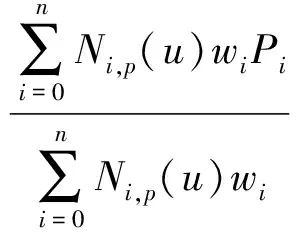
(10)
其中Pi是控制点,wi是权因子,Ni,p(u)是定义在非周期非均匀节点矢量上的p次B样条基函数。
NURBS方法可以通过给定半径R和圆心角γ得到特定的控制点生成圆弧,直线则通过共线的p+1个点生成。
图5给出了使用二次NURBS表达包括圆和直线在内的曲线辅助乘波体设计的示意图,为了控制第一后掠区域的范围,本文增加过渡段,同时使用重节点技术控制曲线保证圆和直线互不干扰。具体实施如下:点AEBFCD为NURBS生成ICC曲线的控制点,其中AEB确定圆弧部分,圆心角为θ1,FCD共线,产生斜率倾角为θ2的直线,BFC点控制圆弧与直线的过渡段。F点的位置很重要,控制了第一后掠区域的大小,也影响了乘波体的总宽度,F点位于圆弧在B点的切线向上,给定参数0≤ω≤1在切线段上控制F点的位置,当ω=0时,F与B重合,方法退化为图4所示的双后掠乘波体设计,当ω=1.0时,F点到达FCT曲线,方法退化为单后掠乘波体设计。
增加了控制参数ω之后,乘波体的平面控制参数可以求得:
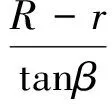
NURBS曲线的节点矢量为[0,0,0,a1,a1,a2,1,1,1],0.0 使用NURBS表达ICC曲线,保证了第一后掠段斜率和曲率的光滑过渡,使乘波体平面形状和表面曲面的过渡更加光顺,同时增加了参数ω控制后掠段的区域大小。设计方法非常灵活(见图6),可以方便改变头部区域和后掠区域的形状,具有给定平面形状设计乘波体外形的能力。编制FORTRAN程序,生成一个外形的时间不超过1秒,效率很高。 2.1 设计变量选择 以双后掠乘波体为例,定平面形状乘波体的设计参数包括圆弧半径R,弯头度ζ,激波角β,ICC曲线的偏转角θ1和θ2,第一后掠区域控制量ω,根据第1.2和第1.3节的分析,通过这些控制参数即可以确定乘波体的长度l,宽度s,弯头区域sb,第一、第二后掠区域s1,s2,第一第二后掠角大小λ1,λ2,下表面厚度分布角ε等形状控制参数。相对应的,也可以通过外形控制参数得到设计参数进行乘波体设计,因此设计变量可以选取设计参数或外形控制参数。简单直观起见,本文选定的设计变量为R,ζ,β,λ1,λ2,ω。 2.2 性能评估方法及验证 使用密切锥进行乘波体设计时,乘波体外形一般从无黏流场出发通过流线追踪得到,所生成的外形中存储有无黏流场信息,因此可以通过流线积分法评估无黏气动力。 高超声速条件下,黏性力在阻力中占有很大的比重,因此在考虑乘波体设计中需要把黏性效应考虑进去。本文使用基于流线的黏性力计算方法[14],将流线与参考温度法结合[15],提高了计算方法的精度。 沿流线计算流线长度并由此计算边界层外缘的当地雷诺数,定义为: (11) x为当地流线长度,ρδ,Uδ和μδ为当地的密度、速度和黏性系数。求得当地雷诺数后,根据下式将其修正为不可压的当地雷诺数: Rexin=FReRexδ 不可压平板的当地黏性力系数计算公式为: 计算得到不可压平板当地黏性力系数后,使用Cfcom=Cfin/Fc修正为可压缩黏性力系数。在这种方法中,修正因子Fc和FRe是与马赫数和温度相关的函数,工程应用中可使用参考温度法[16]计算,参考温度法的思路是将附面层中某处的状态近似的看做物面状态。修正因子与参考量之间的关系为: (12) 式中:μ*=f(T*)为参考黏性系数,可由Sutherland公式求得;ρ*=g(P*,T*)为参考密度,可根据气体状态方程求得。因为附面层中压强的法向梯度为零,所以P*=Pδ。参考温度T*由下式确定: (13) TW是壁面温度,T∞,M∞为自由来流的温度和马赫数。 流线积分法和基于流线的参考温度法作为乘波体的快速预估方法(Waverider estimation, WE)效率很高,但精度不能保证。本文使用计算流体力学(Computational fluid dynamics, CFD)技术对其进行验证计算,计算网格为非结构网格,湍流模型使用S-A模型。设计状态为马赫数Ma=5,高度H=30km,选择外形的设计变量为λ1=75°,λ2=50°,ζ=0.001,ω=0.2,β=14°。 气动力结果如表1所示,CL,CDinv,CDvis分别代表升力系数、无黏阻力和有黏阻力系数,升阻比L/D的误差在4.7%左右,可以看到计算结果是比较相近的,验证了本文乘波体性能快速计算方法的有效性。图7给出了乘波体下表面的等压线,可以看到激波整体附着在前缘,高压区气流整体被束缚在激波内部,具有明显的乘波效应,不考虑底阻的升阻比为6.5左右,保持了设计状态的高升阻比特性。图8给出了设计激波曲线与CFD模拟结果的对比,激波形状除在转折处存在误差外在大部分拟合的都很好,也说明了设计方法的有效性。在转折处本文未严格按照NURBS的曲率设定锥形流尺度,而是使曲率逐渐过渡,这样处理保证了过渡段的曲面光滑,但对乘波体的气动性能有一定的影响。 表1 尖头乘波体CFD气动力验证Table 1 CFD validation of the cusp waverider 2.3 激波角和后掠角的影响 考查激波角和后掠角对乘波体性能的影响。如未特别指出,设计状态默认为H=30km,Ma=8。当Ma=8时马赫角为7.18°,此为激波角的最小值,后掠角的上限为82.82°[11]。除了气动性能,容积在飞行器设计中也必须考虑,一般定义容积率τ=V2/3/S为评价指标,V是容积,S为平面投影面积。 图9给出了几个不同后掠角组合乘波体的升阻比和容积率随激波角的变化,设计参数ω=0.2,ζ=0。从图9可以看出,升阻比在β=10°左右取得最大值,且随β增大而降低;λ1越小同等激波角下的升阻比越大;容积率随β增大而升高。图9给出了升阻比-容积率关系,对于乘波体构型,容积率一般选择在0.1以上,否则工程实用价值较低,当τ>0.1时,形成了类似于多目标优化中的Pareto前沿面,此时后掠角75~75°(λ1=75°,λ2=75°)组合的性能较好。 对于双后掠乘波体外形,后掠角λ1和λ2对乘波体的性能都有影响,并且容积率受λ2影响很大。以图9中的55-40°和75-50°外形为例,因为λ2较小,容积率甚至比51-45°和65-60°组合更低。 当固定λ2时,同等β下λ1越大,升阻比越小,容积率升高。图10(a)为固定λ2=45°时的升阻比-容积率曲线,在τ>0.1时,形成Pareto前沿面,最优外形集在λ1较大时取得。 当固定λ1时,同等β下λ2越大,升阻比越小,但容积率升高。图10(b)给出了固定λ1的升阻比-容积率曲线,最高点位置随λ2的增大右移,Pareto前沿面直到τ>0.15才完全形成。在考虑升阻比-容积率的综合性能时,可以适当减小λ2以获得最优外形。 综合图9和图10,修改后掠角不会对乘波体的气动性能带来质的减小,虽然容积率有所下降,但第一后掠角对应的机身部分保持不变,提供了主要的装载空间,有效容积不会减小太多。 2.4 弯头和后掠区域参数的影响 ζ控制弯头区域的大小,当ζ接近0时,生成的外形是尖头双后掠乘波体,也被称作涡升力乘波体[17]。当ζ>0时得到弯头双后掠外形。ζ(∈[0,1])大小表示弯头程度。 图11给出了ζ对升阻比的影响,随着ζ增加,当β小于10°时,升阻比下降;在激波角大于10°时,升阻比增加。ζ对容积率影响很小。当激波角小于10°时,乘波体很薄,影响规律相反,这也与第2.3节中的分析相符,具体影响还要后续细致研究。 考查后掠区域控制参数ω对乘波体性能的影响,图12给出了ω对升阻比的影响,随着ω增加,升阻比下降(除β=8°外),此时容积率略微增加,对应第2.3节中的分析结果。 1) 密切锥乘波体设计中存在两个重要的全域性几何关系,据此提出定平面形状乘波体概念,并重点分析了双后掠外形。结合NURBS表达曲线辅助设计,提高了设计灵活性,保证曲面光滑,也方便提取设计变量。 2) 后掠角最大的乘波体外形处于升阻比和容积率较优的位置,随激波角的增大升阻比先增大后减小,容积率逐渐增大;不同后掠角组合对升阻比和容积率都有影响,在考虑升阻比/容积率的综合性能时,可以适当减小第二后掠角以获得最优外形;升阻比随弯头度和后掠区域影响参数的变化趋势与激波角和后掠角有关。 3) 考虑黏性的气动力快速评估方法效率很高,本文通过CFD方法验证了设计和评估方法的有效性。双后掠乘波体保持了高超声速状态的性能优势,后续工作中需进一步研究平面形状对乘波体非设计点性能的影响,探索兼顾低速性能的乘波体气动外形的设计方法。 [1] Nonweiler T R. Aerodynamic problems of manned space vehicles [J]. Journal of Royal Aeronautical Society, 1959, 63(1):521-530. [2] Jones J G, Moore K C, Pike J, et al. A method for designing lifting configurations for high supersonic speeds using axisymmetric flow field [J]. Archive of Applied Mechanics, 1968, 37(1): 56-72. [3] Rasmussen M L. Waverider configurations derived from inclined circular and elliptic cones [J]. Journal of Spacecraft and Rockets, 1980, 17(6): 537-545. [4] 刘传振, 白鹏, 陈冰雁. 三维流场乘波体快速设计方法及多目标优化[J]. 宇航学报, 2016, 37(5): 535-543. [Liu Chuan-zhen, Bai Peng, Chen Bing-yan. Rapid desing and multi-object optimization for waverider from 3D flow[J]. Journal of Astronautics, 2016, 37(5) : 535-543.] [5] Marcu A L, Kojiro S. Experimental investigation of a Mach 3.5 waverider designed using computational fluid dynamics [J]. AIAA Journal, 2015, 53(6): 1590-1601. [6] Sobieczky H, Dougherty F C, Jones K. Hyper-sonic waverider design from given shock wave [C]. The First International Waverider Symposium, University of Maryland, MD, USA, 1990. [7] 王发民, 丁海河, 雷麦芳. 乘波布局飞行器宽速域气动特性于研究[J]. 中国科学E辑: 技术科学, 2009, 39(11): 1828-1835. [Wang Fa-min, Ding Hai-he, Lei Mai-fang. Aerodynamic characteristics research on wide-speed range waverider configuration [J]. Sci China Ser E-Tech Sci, 2009, 39(11): 1828-1835.] [8] 贾子安, 张陈安, 王柯穆,等. 乘波布局高超声速飞行器纵向静稳定特性分析[J]. 中国科学E辑: 技术科学, 2014, 44: 1114-1122. [Jia Zi-an, Zhang Chen-an, Wang Ke-mu, et al. Longitudinal static stability analysis of hypersonic waveriders [J]. Sci China Ser E-Tech Sci, 2014, 44: 1114-1122.] [9] Starkey R, Lewis M. A Simple analytical model for parametric studies of hypersonic waveriders [C]. The 8th International Space Planes and Hypersonic Systems and Technologies Conference, Norfollk, VA, USA, Apr. 27-30, 1998. [10] Patrick E R. Geometrical relations for osculating cones and osculating flowfield waveriders [C]. The 49th Aerospace Science Meeting, Orlando, Florida, Jan. 4-7, 2011. [11] 段焰辉, 范召林, 吴文华. 定后掠角密切锥乘波体的生成和设计方法研究[J]. 航空学报, 2016, 37(10): 3023-3034. [Duan Yan-hui, Fan Zhao-lin, Wu Wen-hua. Research on the methods of generation and design of osculation cone waverider with constant angle of sweepback [J]. Acta Aeronoutica et Astronautica Sinica, 2016, 37(10): 3023-3034.] [12] Jones K D, Center K B. Waverider design methods for non-conical shock geometries [R]. The 3rd Theoretical Fluid Mechanics Meeting, St.Louis, Missouri, USA, June 24-26, 2002. [13] Les P, Wayne T. The NURBS Book, 2nd Edition[M]. Springer-Verlag, New York, 1997: 202-227. [14] 段焰辉. 高超声速飞行器气动外形优化设计方法研究[D]. 西安: 西北工业大学, 2013. [Duan Yan-hui. Research on methods of aerodynamic shape optimi-zation for hypersonic vehicles[D]. Xi'an: Northwestern Polytechnical University, 2013.] [15] Corda S, Anderson J. Viscous optimized hypersonic waveriders designed from axisymmetric flow fields [C]. The 26th Aerospace Sciences Meeting, Revo, NV, USA, Jan. 11-14, 1988. [16] Anderson J D. Fundamentals of aerodynamics [M]. The 3rd edition. McGraw-Hill Companies, USA, 2001. [17] Patrick E R. Vortex lift waverider configurations [C]. The 50th Aerospace Science Meeting, Knoxvell, Tennessee, USA, Jan. 9-12, 2012. 刘传振(1989- ),男,博士生,主要从事飞行器气动外形设计。 通信地址:北京7201信箱16分箱(100074) 电话:13161912959 E-mail: chuanzhenliu@gmail.com (编辑:牛苗苗) Analysis on Design Variables for Planform-Controllable Waverider LIU Chuan-zhen, BAI Peng, CHEN Bing-yan, ZHOU Wei-jiang (China Academy of Aerospace Aerodynamics, Beijing 100074, China) The concept of one planform-controllable waverider is proposed to extend the flexibility of the osculating waverider design. The universal geometry relations between the design and planform parameters are deducted, and employing the non-uniform rational B-spline in representing the design curve to aid design, the article builds the method of the double swept waverider generation in which the blunt area and swept area are controllable. The design variables are extracted to customize the planform of the waverider. The rapid aerodynamic assessment including viscous effect, validated with the CFD technique, is applied to analyze the influence of the design variables for waverider properties. The research shows that the hypersonic high L/D property of the waverider remains with the modified planform and lays the solid foundation to design the novel waverider configurations. Waverider; Planform-controllable; Double swept; Design Variables; Aerodynamic characteristics 2016-10-19; 2017-03-17 国家自然科学基金(11672281) TP731 A 1000-1328(2017)05-0451-08 10.3873/j.issn.1000-1328.2017.05.0022 设计变量影响分析
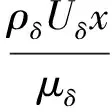
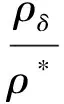
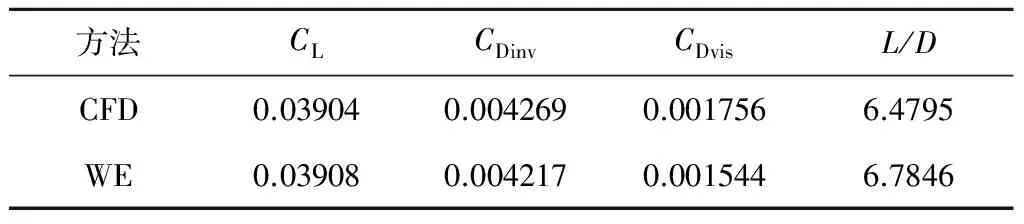
3 结 论

