便携式医疗设备中高精度温控系统的仿真与研究

闫子旭+曹丽亚+年雷+高铭良+刘爽+孙毅

摘 要：為解决便携式医疗设备中高精度温控系统的温度补偿问题，本文采用粒子群算法，建立系统补偿器模型，并进行模块仿真研究。使用MATLAB-Simulink搭建动态温控系统模型与补偿器模型，进行仿真分析。仿真结果显示，该方法使动态温控系统在响应速度与超调量上得到明显改善。

关键词：医疗设备；温度控制；粒子群算法

DOI：10.16640/j.cnki.37-1222/t.2017.11.257

0 引言

针对温度检测的精度和时效性问题，本文基于粒子算法，根据传感器动态补偿原理提出了一种可连续高精度调温的温度监测和控制系统，实现对温度的实时检测，具有提醒和控制的功能。此系统功能强大，便于携带，是一款既实用又廉价的控制系统，可广泛应用于医疗器械、温室及冷藏等设备中。

1 补偿器实现

补偿模块多以数字滤波器的形式实现，将实际数字滤波补偿器的补偿原理以差分方程形式表示

（1）

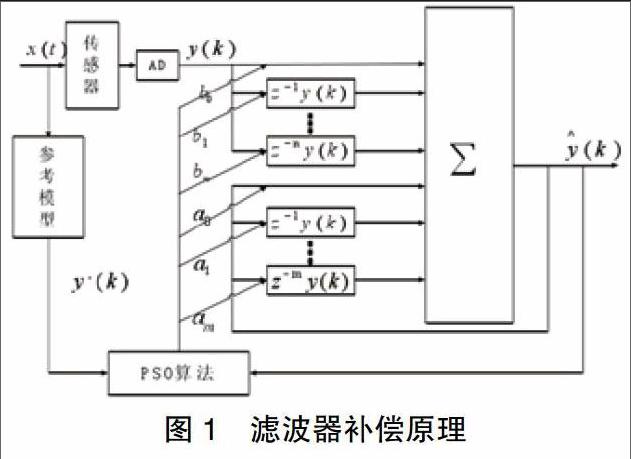
其中：为输出信号，为输入信号，为噪声，为延迟算子， 为阶次，为补偿系数。根据补偿差分方程，可以确定应用粒子群算法进行系统动态补偿的原理，如图1所示。如何确定补偿系数是粒子群算法要解决的核心问题，应用粒子群算法确定参数，关键是确定方法的适应度函数J与惯性系数w[1]。

其中： 温度系统实际输出， 为理想输出， 为样本数量。适应度函数衡量了实际输出与理想输出之间存在的误差大小，是判断迭代终止的条件之一[2]。

惯性系数直接决定了搜索速度与最终效果，惯性系数过大，当w取值很大时，有利于全局探寻最佳而不利于局部寻找最佳[3]；当w取值相对小时，则对于局部探寻是有意义的[4]。基于以上因素，确定惯性系数迭代公式

由上式可以看出，惯性系数初始值较大，随着迭代次数增加，逐渐减小，有利于全局最优解的确定[5]。

2 仿真结果

根据上文理论分析，对动态温度系统以及补偿模块进行仿真分析。在MATLAB软件中的Simulink模块中，通过不同参数的设置，对该模型与补偿器进行仿真验证。

补偿前系统超调量为1.65，稳态时间为10-4数量级，稳态误差为0.02。可以看出补偿前系统单位阶跃响应存在较大的超调量，同时稳态时间不够理想。对于补偿模块，采用四阶模型，由粒子群算法计算，确定补偿模块个参数为

对应补偿器各个参数，对补偿前后分别施加单位阶跃输入，进行补偿前后单位阶跃响应对比。由图2可知，上图为补偿前传感器的单位阶跃响应曲线，下图为补偿后的响应曲线。由响应曲线对比可以看出，补偿后系统响应超调量，1.65下降到1.07，超调量与系统震荡得到比较明显的改善；稳态时间由10-4数量级下降到6.5×10-6，稳态时间得到了数量级的下降；稳态误差由0.02下降到0.0005以下。对比补偿效果可知，补偿后系统动态性能明显改善，响应曲线在速度与精度上能够比较好的反映输入信号。

对比补偿前后的温度系统幅频特性，在幅值误差为2%时，系统工作频带由补偿前的4×105拓宽到1.44×106。理论上系统经过补偿后可以任意拓宽工作频带[6]，但实际进行补偿，不可能无限拓宽频带，因为噪声信号通常为高频，工作频道包含高频噪声会导致噪声放大，甚至有淹没有用信号[7]，使得测量无法进行。因此，频带拓宽为传感器的 倍即可。

3 结束语

针对以往补偿器过于依赖系统模型这一因素，本文应用粒子群算法对动态温度系统进行补偿从而改善系统动态性能，具有一定的推广价值。此系统功能强大，便于携带，是一款既实用又廉价的控制系统，可广泛应用于医疗器械、温室及冷藏等设备中。

参考文献：

[1]邱宪波，袁景淇.带前馈补偿的基因扩增反应高精度温控系统，2005，26（08）：831-844.

[2]Philip Yu， Takhisov. Using of thermoelectric modules for heat exchange intensification.Proceedings of 20thInternational Conference on Thermoelectrics，2001（03）：467-469.

[3]孙以材，魏占永，孙新宇，高振斌，刘惠丽.压阻型压力传感器的零点温漂及其补偿技术[J].半导体杂志，1999（04）：40-49.

[4]KOVACIC I，BRENNAN M J，LINETON B.On the resonance response of an asymmetric Duffing oscillator[J].International Journal of Non-Linear Mechanics，2008，43（09）：858-867.

[5]轩春青，轩志伟，陈保立.基于最小二乘与粒子群算法的温度传感器动态补偿方法[J].传感技术学报，2014（10）：1363-1367.

[6]欧阳承曦.硅压阻式压力传感器高精度温度补偿技术研究[D].电子科技大学，2015.

[7]VIRGIN L，DAVIS R.Vibration isolation using buckled struts[J].Journal of Sound Vibration，2003（260）：965-973.