基于贝叶斯方法的光合作用生化模型参数估计及其在干旱区葡萄上的应用*

朱中华,韩 拓,柳金权,朱高峰

(1.甘肃省水利水电学校 兰州 730021;2.兰州大学资源环境学院/西部环境教育部重点实验室 兰州 730000; 3.华亭县水务局 华亭 744100)

基于贝叶斯方法的光合作用生化模型参数估计及其在干旱区葡萄上的应用*

朱中华1,韩 拓2**,柳金权3,朱高峰2

(1.甘肃省水利水电学校 兰州 730021;2.兰州大学资源环境学院/西部环境教育部重点实验室 兰州 730000; 3.华亭县水务局 华亭 744100)

以无核白葡萄为试材,测定了其在不同季节(6—9月)、不同胞间CO2浓度下的净光合速率,根据贝叶斯方法,结合蒙特卡罗马尔科夫链算法对光合生化模型参数进行估算,以期获得不同季节的模型参数值,并与最小二乘法所得结果对比,探讨贝叶斯方法在解决高维度复杂模型参数估计问题中的可行性和葡萄光合作用关键参数季节变化规律。结果表明,最大羧化速率(Vcmax)、最大电子传递速率(Jmax)、磷酸丙糖利用速率(TPU)均有明显的季节变化特性,出现先增后减的趋势,8月达最高,分别为54.30µmol∙m-2∙s-1、88.45µmol∙m-2∙s-1和6.56µmol∙m-2∙s-1;9月最小,分别为34.66µmol∙m-2∙s-1、58.86µmol∙m-2∙s-1和4.38µmol∙m-2∙s-1。叶肉导度(gm)在各个月份波动不大,6—9月分别为5.16µmol∙m-2∙s-1∙Pa-1、5.29µmol∙m-2∙s-1∙Pa-1、5.39µmol∙m-2∙s-1∙Pa-1和5.41 µmol∙m-2∙s-1∙Pa-1。与传统的最小二乘法相比,贝叶斯方法估算的Vcmax值偏小,Jmax、TPU和gm无明显差异。同时贝叶斯方法估计出的模型参数是在考虑参数先验信息的基础上获得的,生化意义更加显著。试验表明,光合作用生化模型(FvCB模型)在应用于光合作用模拟时,应充分考虑其参数的季节变化性;结合蒙特卡罗马尔科夫链算法的贝叶斯参数估计能更有效解决FvCB模型中参数估计问题。

干旱区;葡萄;贝叶斯参数估计;光合作用生化模型;光合作用参数;季节变化

近年来,光合作用的模型研究得到人们日益关注[1-2]。其中,von Caemmerer等[3-6]的光合作用机理模型(以下简称FvCB模型)因具有明确生物学意义而被广泛应用于光合作用研究中,并被多数碳循环模型(如SiB、CLM等)所采用。在该模型中,最大羧化速率(Vcmax)、最大电子传递速率(Jmax)、磷酸丙糖利用速率(TPU)是表征植物光合能力的关键参数。如何利用实测净光合速率/胞间CO2浓度变化曲线(A/Ci曲线)估计这些参数不仅是植物生态学研究的热点,也是提高陆地碳循环模拟精度的关键[7]。

前人以不同植物为研究对象对模型参数估计做了较多研究。Harley[8]等和Wullschleger[9]用分段估计法对棉花(Gossypiumspp.)和 109种 C3植物的Vcmax,、暗呼吸速率Rd和叶肉导度gm进行了估计,但此类方法以胞间CO2浓度分压等于20 Pa为节点进行数据的经验性分割,不但受人为因素扰动较大,而且当数据集较小时收敛较为困难;Dubois等[10]和Miao等[11]结合格点搜索利用非线性最小二乘法同时估计出Vcmax、Jmax、TPU和Rd,但该方法是以求误差的最小值来逼近参数真值,较适用于连续性函数的参数估计,而对于分段不连续且高维的FvCB模型难以获得全局最优结果;Su等[12]将遗传算法应用到FvCB模型主要参数的估计当中,克服了传统迭代方法容易陷入局部最优解的缺陷,但该算法后期适应度容易趋向一致,使优秀的个体在产生后代时优势不明显,导致算法进化后期搜索效率较低;近年来,Zhu等[13]和Feng等[14]先后将贝叶斯方法应用到光合作用模型参数估计当中,较其他方法有明显的优势。与其他参数估计方法相比,贝叶斯方法在充分考虑观测误差和模型结构误差的基础上,获得参数的分布范围,大大提高了拟合精度。然而将该方法应用于光合作用生化模型参数估计,获取适用于我国西北干旱区葡萄的模型参数的研究尚鲜见报道。

本文以我国西北干旱绿洲典型农田生态系统经济作物葡萄(Vitis vinifera)为研究对象,利用便携式光合作用-荧光测量系统获取不同季节葡萄净光合速率随胞间CO2浓度变化的数据。在此基础上,应用贝叶斯方法对FvCB模型参数进行估计,并分析其与叶片特性的关系,以验证贝叶斯方法在解决高维度复杂模型参数估计问题的可行性,并估计出模型参数和具有的生化意义,揭示葡萄光合作用关键参数季节变化规律及其与叶片特性的关系,增进对干旱绿洲典型经济作物葡萄光合特征的认识,为提高农田生态系统的产量提供科学指导,推动贝叶斯方法在植被光合作用模型参数估计研究上的应用。

1 研究区概况

试验地位于甘肃省敦煌市阳关镇南湖绿洲西南部,距市区约70 km,东、南、北三面环山(三危山、祁连山、北塞山),西接塔克拉玛干沙漠,观测点地理坐标为39°53′N,94°07′E,海拔1 100～1 297 m;深居内陆,属暖温带干旱性气候,日照时间长,昼夜温差大,降水稀少,蒸发量大,年均降水量36.9 mm,年均潜在蒸发量达 2 486 mm[15]。年日照时数为3 115～3 247 h,年均气温9.3℃;土壤主要为隐域性土壤,包括沼泽土、草甸土和盐渍土等。观测点位于南湖绿洲西南部,属农田生态系统,土壤类型为绿洲灌耕土,葡萄园每月下旬进行一次人工大水漫灌,确保植物在充分供水条件下生长。

2 材料与方法

2.1 试验材料

试验材料为‘无核白葡萄’(Thompson Seedless),平均冠层高度1.84 m,平均胸径3.2 cm,树龄13 a。随机选取4棵植株,利用便携式光合作用-荧光测量系统(GFS-3000)进行CO2响应曲线(A/Ci)测定。观测日期分别为2014年的6月、7月、8月、9月,涵盖了葡萄的开花期、坐果期、浆果生长期、浆果成熟期4个典型生长期。观测时间处于每月中下旬某一晴天的10:00—16:00。观测叶片则选取位于冠层中上部的成熟阳生叶片,用于不同季节自然条件下的活体测定,每株选3片叶子进行重复试验。

测量前,使叶片处在饱和光照条件下(PARtop=1 200 mol∙m-2∙s-1)适应30 min,此时酶活性被完全激活。6、7、8、9月叶室温度(Tcuv)分别设置为25℃、30℃、30℃和20℃,保证了与当月自然环境温度的一致性。环境大气压强(Pamb)为86 kPa,叶片温度(Tleaf)设定范围为24～34℃,样品室相对湿度(RH)控制在40%～65%,均处在当月光合作用的最佳范围内,气流速率为750µmol∙s-1,保证了CO2的充分吸收。在以上设置不变的情况下,调整CO2绝对浓度(CO2abs)来完成不同植株、不同叶片在不同季节的A/Ci曲线测定。CO2abs最初设为120 kPa,而后为100 kPa、80 kPa、60 kPa、50 kPa、40 kPa、30 kPa、20 kPa、10 kPa和5 kPa共10个水平,在每个CO2浓度下适应2～3 min后开始测定,且每个梯度记录3次,求均值。

2.2 模型简介

FvCB模型将整个光合作用过程划分为3个限制阶段:二磷酸核酮糖羧化酶限制阶段(Rubisco限制)、二磷酸核酮糖再生限制阶段(RuBP限制)和磷酸丙糖利用限制阶段(TPU限制),其表达式为[3-5]:

式中:An为净光合速率(µmol∙m-2∙s-1),Ac、Aj和Ap分别为Rubisco限制、RuBP限制和TPU限制阶段的净CO2同化速率(µmol∙m-2∙s-1),Vcmax为最大羧化速率(µmol∙m-2∙s-1),J为电子传递速率(µmol∙m-2∙s-1), TPU为磷酸丙糖利用速率(µmol∙m-2∙s-1),Rd为暗呼吸速率(µmol∙m-2∙s-1),f*为CO2补偿点(Pa),A为光合速率(µmol∙m-2∙s-1),Kc和Ko分别为羧化作用和加氧作用的米氏常数(kPa和Pa),Cc和o分别为Rubisco中CO2分压(Pa)和O2分压(21 kPa)[16],Jmax为最大电子传递速率 (µmol∙m-2∙s-1),gm为叶肉导度(µmol∙m-2∙s-1∙Pa-1),Ci为胞间CO2浓度(Pa),θ为光响应曲线斜率(0.90),a为电子转移的量子产率(0.30),Q为光合作用量子通量密度(0.093µmol∙m-2∙s-1)[7]。

2.3 参数估计方法

贝叶斯定理认为,参数的后验分布与先验分布和概率密度函数的乘积成正比[17],其表达式为:

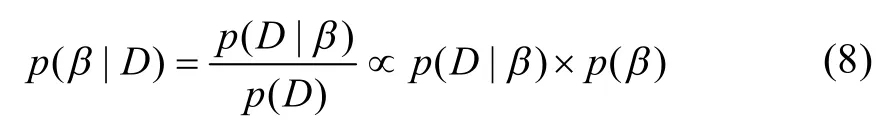
式中:b为由待估参数构成的参数向量(包括Vcmax、Jmax、TPU和gm),D为观测数据,p(b|D)为后验分布,p(D|b)为抽样分布的概率密度函数,p(b)为待估参数b的先验概率分布,p(D)为随机变量的边缘分布。样本抽取采用Markov Chain Monte Carlo MCMC)方法[18-20]。

最小二乘法在FvCB模型参数估计中应用较早,其基本思想是通过最小化误差的平方和寻找数据的最佳函数匹配[10]。假设有一组数据xi,yi,i=1,2,…,N,且已知该组数据满足a为待定参数向量,则最小二乘法的目标是求出一组待定参数值,可以定义出最优化问题,如下:

3 结果与分析

3.1 光合作用参数估计结果

以无核白葡萄为研究对象,同时选用最小二乘法和贝叶斯方法对FvCB模型运用同一套观测数据集进行参数估计(图1)。从图中可以看出:无论是贝叶斯方法还是最小二乘法,参数季节变化显著。对于参数Vcmax、Jmax和TPU,其值呈先增大后减小的趋势,8月达到最大,9月最小;而gm则是6月和9月略大于7月和8月,且两种参数估计结果的季节变化规律一致。值得注意的是,传统的最小二乘法获得的参数估计结果是一个定值,而基于贝叶斯方法的估计结果不但可以获得参数估计结果的中值,还可以获得参数的分布范围。此外,从表1可以看出,最小二乘法估计出的参数Vcmax在4个月中均大于贝叶斯方法估计结果,最大差别可达15.51mmol∙m-2∙s-1(9月),而参数Jmax、TPU和gm无此现象。

图1 不同月份基于贝叶斯后验分布及最小二乘法的葡萄光合参数估计结果(I代表贝叶斯后验分布范围)Fig.1 Posterior mean estimates results given by the Bayesian method and the least square method estimation results of grape photosynthetic parameters in different months(I represents posterior distribution ranges based the Bayesian method)

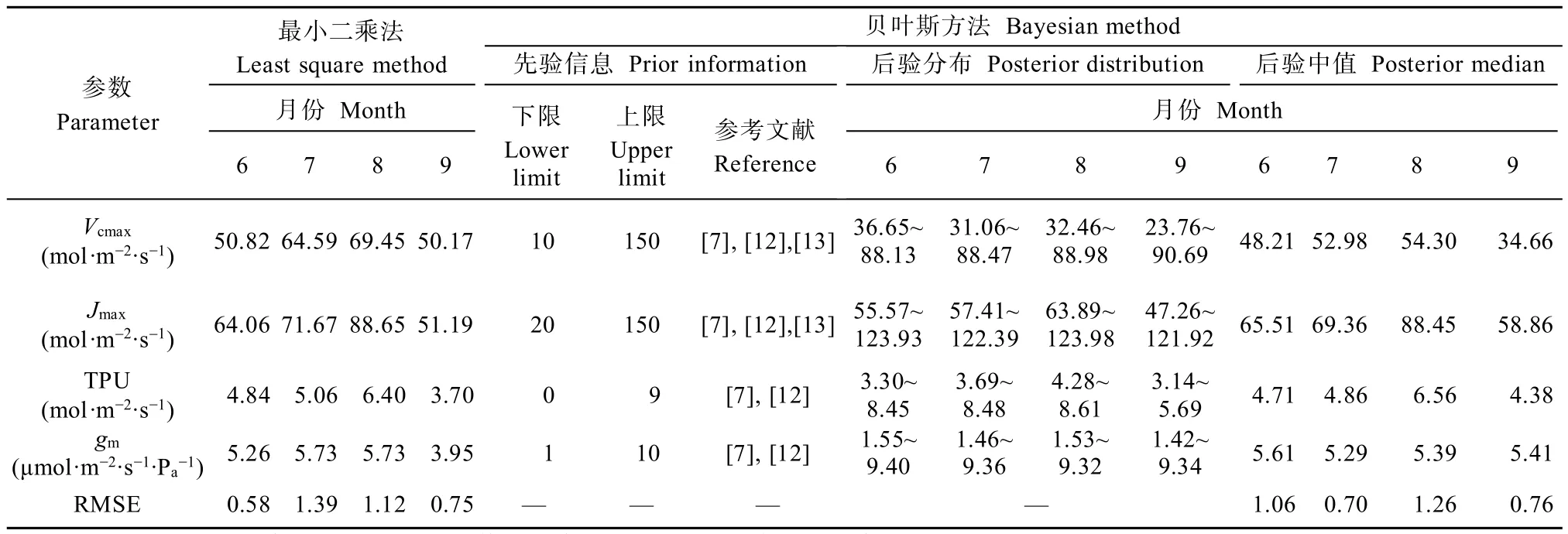
表1 不同月份基于最小二乘法参数估计结果和基于贝叶斯方法的参数先验信息与估计结果Table 1 Parameters estimation results based on the least square method and the prior information and estimation results based on the Bayesian method in different months for grape photosynthesis

与最小二乘法不同,贝叶斯方法是一种参数区间估计方法,其目标不是在参数可行区间内找到一个使模型模拟效果最好的最优参数组合,而是在充分考虑先验信息误差的前提下在一定的置信水平上估计模型参数的分布区间。从不同月份参数的先验信息及后验分布结果可以看出(表1):基于先验信息的贝叶斯参数估计方法可以有效地缩小给定的参数先验分布范围。定义UR(uncertainty reductions)为参数不确定性相对减小量(UR=1-CIposterior/CIprior,其中CIposterior和CIprior分别为后验分布和先验分布的95%置信区间)[21],则对参数Vcmax、Jmax和TPU,在不同月份其不确定性相对减小量近50%,最高达72%;而对于gm,UR值相对较小,仅略大于10%(表2)。由此可见,参数Vcmax、Jmax和TPU收敛效果很好,在贝叶斯方法下可被很好地估计。

表2 95%置信区间下葡萄光合参数不同月份后验分布相较于先验分布的不确定性相对减小量Table 2 Relative uncertainty reductions in the length of 95% credible interval form prior to posterior distribution of grape photosynthesis in different months %

3.2 基于观测值和模拟值的模型评价

在不同胞间CO2浓度下,基于贝叶斯方法的净光合速率估计值(Ansim)和净光合速率观测值(Anobs)的线性回归如图2所示,可以看出:4个月的相关系数均较高,R2均在0.90以上;同时,各月观测/拟合趋势线趋近于1∶1直线,且在8月和9月更为显著(表3)。此外,与最小二乘法相比,贝叶斯方法所得观测/拟合数据点整体分布在更加靠近1∶1直线的区域,充分表明贝叶斯方法具有更强的收敛性,获得了更高精度的参数估计结果。

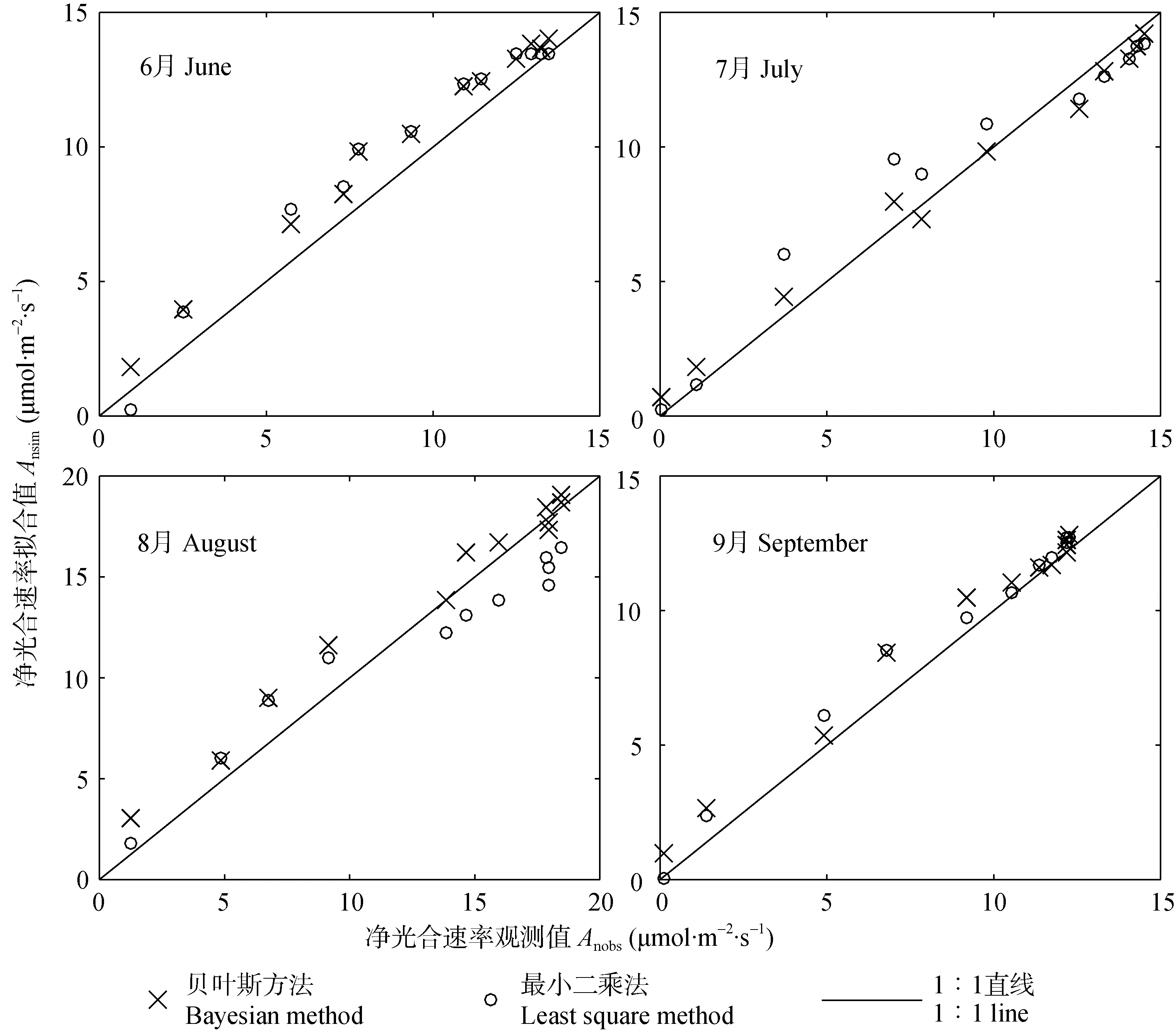
图2 不同月份葡萄净光合速率观测值和贝叶斯方法及最小二乘法拟合的线性回归Fig.2 Regressions of grape net photosynthesis rate between measured value(Anobs)and modeled value(Ansim)by the Bayesian method and the least square method in different months

光合作用对胞间CO2浓度的响应曲线(A/Ci曲线)是分析光合作用机理的重要指标。将不同方法的参数估计结果应用于FvCB模型,A/Ci曲线拟合结果如图3所示。从图中可以看出:对于贝叶斯方法的拟合结果,净光合速率(An)随胞间CO2浓度(Ci)的升高呈现出明显的3个阶段,与FvCB模型结构相吻合,即:当Ci相对较低时,An随Ci的升高呈直线快速上升,此时处于光合作用第1阶段——Rubisco限制阶段;随着Ci的变大,An随Ci升高的增速逐渐变小,此时处于第2阶段——RuBP限制阶段;当Ci继续增大到一定数值时,An不再随Ci的升高而变大,而是趋于稳定,此时处于第3阶段——TPU限制阶段。且4个月第1阶段和第2阶段转折点对应的Ci分别为31.68 Pa、48.19 Pa、50.82 Pa和35.67 Pa,出现了明显的季节差异性。此外,不同月份最大净光合速率分别为:13.49mmol∙m-2∙s-1、15.32mmol∙m-2∙s-1、18.49mmol∙m-2∙s-1、12.28mmol∙m-2∙s-1,与参数估计结果有相同的季节变化规律。而对于最小二乘法的拟合结果,尽管确保了均方根误差保持在较小的范围,由于估计时参数之间的相互作用,只拟合出了二磷酸核酮糖再生限制阶段(RuBP限制)和磷酸丙糖利用限制阶段(TPU限制),导致了生理生态学意义不够明显。可见,相较于最小二乘法,贝叶斯方法可以估计出具有生化意义的模型参数,参数优化后的FvCB模型可用于模拟我国西北干旱绿洲作物的光合速率。

表3 基于贝叶斯方法的葡萄不同月份净光合速率观测值(Anobs)和拟合值(Ansim)的统计信息Table 3 Statistical information of measured(Anobs)and estimated(Ansim)values of net photosynthesis rate of grape based on the Bayesian method in different months

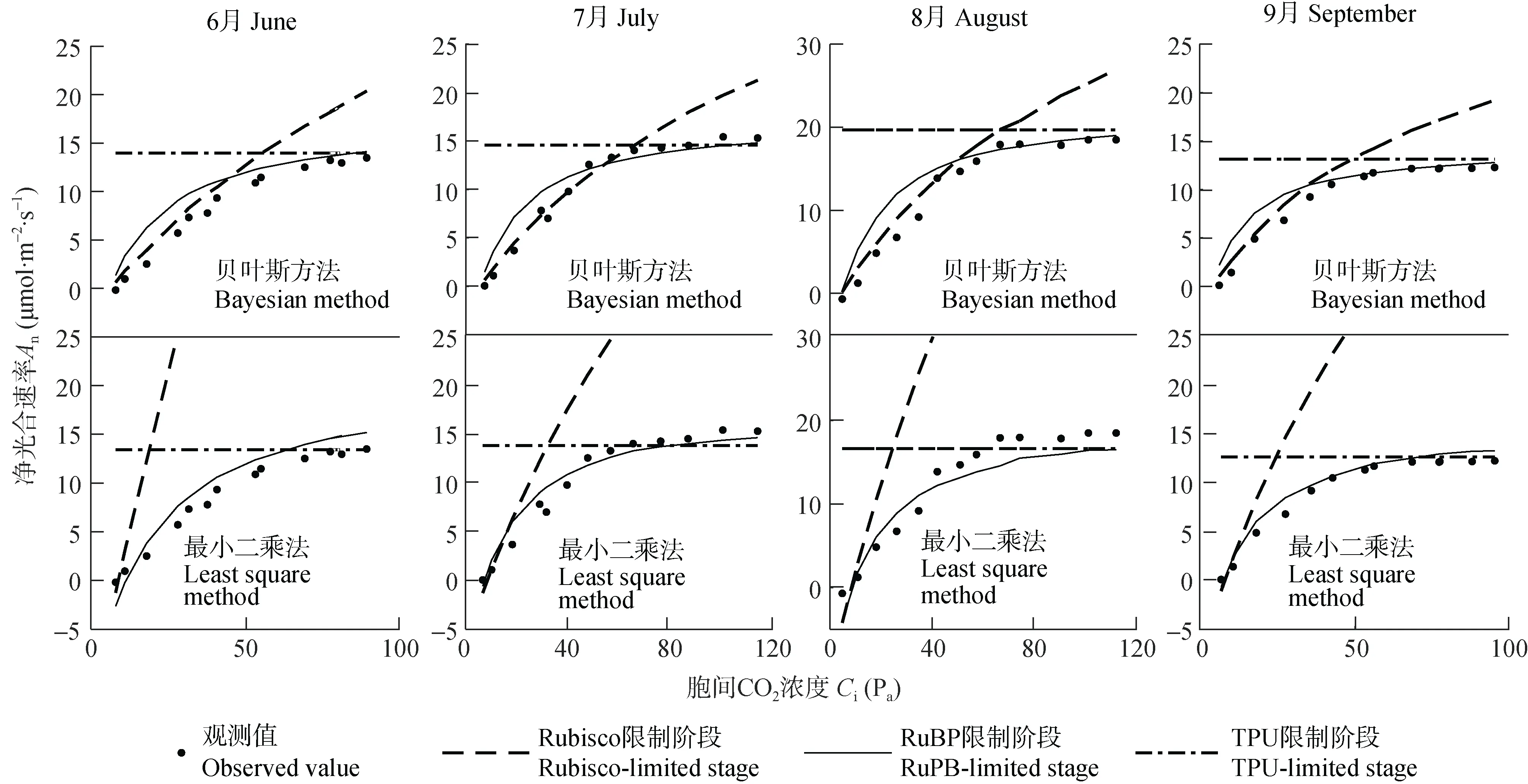
图3 不同月份葡萄净光合速率随细胞间二氧化碳浓度(Ci)变化趋势图Fig.3 Prediction of net photosynthesis rate(An)of grape as a function of intercellular carbon dioxide concentration(Ci)in different months

4 讨论

无核白葡萄为多年生木本,参数Vcmax、Jmax和 TPU 的估计范围与 Wullschleger[9]结果相似, Wullschleger选取了109种C3植物,基于A/Ci曲线的非线性回归技术估计了不同植被类型的参数值,给出参数变化范围:Vcmax为6～94mmol∙m-2∙s-1,Jmax为17～372mmol∙m-2∙s-1,TPU为4.9～20.1mmol∙m-2∙s-1,其中一年生草本植物参数值大于多年生木本植物。本文利用贝叶斯方法精准地估计了模型参数,且结果在前人所给结果范围内。同时,传统参数估计方法:如Harley等[8]利用分段方法估计出了Vcmax、Rd和gm,但该方法将A/Ci曲线中Rubisico限制阶段和RuBP限制阶段的转折点设为定值,而本文贝叶斯拟合结果显示出转折点明显的季节差异性,反映出分段估计法受人为分割的扰动会产生较大误差; Sharkey等[7]用微软电子表格同时估计出Vcmax、Jmax、TPU、Rd和gm;Dubois等[10]和Miao等[11]结合了格点搜索和非线性最小二乘法估计出Vcmax、Jmax、TPU和Rd,这些方法都是派生的最优化方法,不但计算量较大、对初始值的设定十分敏感,而且适用于连续函数的参数估计,而对于分段不连续的FvCB模型难以得出全局最优结果。相反,贝叶斯方法不需要通过求导函数实现目标函数的最小化,同时又结合了先验信息,所以该方法在解决高维复杂不连续函数的参数估计问题上有很大优越性。本文首次将该方法应用在我国西部极端干旱的敦煌绿洲,准确估计了当地主要经济作物葡萄在典型生长季(6月、7月、8月和9月)内不同阶段(开花期、坐果期、浆果生长期、浆果成熟期)的模型参数,对提高农田生态系统的产量有一定指导,为陆地生态系统碳循环模型研究提供一定的借鉴。

不同月份参数估计结果表现出明显的季节差异,与葡萄在不同季节氮分配策略相关。无核白葡萄为C3植物,约60%～80%的叶片氮以核酸和酶的形式存在于叶片中[22-23]。前人研究表明,叶片含氮量与光合作用能力存在正相关关系[24-25]。在光合能力较强的月份,所需氮素多,酶活性强;反之,光合能力较弱的月份,氮素消耗较少,酶活性较弱[26-27]。Vcmax是Rubisco限制阶段的最重要参数,此时CO2的固定受Rubisco活性的制约,所以在8月,参数Vcmax也处于最大值;而在以9月份为代表的浆果成熟期,叶片趋于衰老,酶活性较弱,在无大量氮素消耗时,叶片氮向木质部转移贮存,参数Vcmax也出现较低值。同理,分别作用于RuBP限制阶段和TPU限制阶段的参数Jmax和TPU也表现出相同的季节变化特性。而参数gm则受温度和太阳辐射影响较大,7月和8月相较于6月和9月具有较高的温度和较强的太阳辐射,此时叶片为防止大量蒸发失水,会出现气孔关闭情况,从而导致较小的气孔导度。

5 结论

1)基于贝叶斯方法估计出FvCB模型中4个主要参数范围:最大羧化速率(Vcmax)为23.76～90.69mmol∙m-2∙s-1,最大电子传递速率(Jmax)为47.26～123.98mmol∙m-2∙s-1,磷酸丙糖利用速率(TPU)为3.14～8.61mmol∙m-2∙s-1,叶肉导度(gm)为1.42～9.40mmol∙m-2∙s-1∙Pa-1。

2)参数大小存在明显的季节变化规律,最大羧化速率(Vcmax)、最大电子传递速率(Jmax)和磷酸丙糖利用速率(TPU)参数大小出现先增后减的趋势,8月最大9月最小,气孔导度(gm)则6月和9月略大于7月和8月。

3)与传统的最小二乘法相比,贝叶斯参数估计能够有效解决高维度复杂不连续模型的参数估计问题,可以基于观测数据有效估计出具有生化意义的合理参数值。

References

[1]Hansen J,Kharecha P,Sato M.Climate forcing growth rates: Doubling down on our Faustian bargain[J].Environmental Research Letters,2013,8(1):011006

[2]Yvon-Durocher G,Allen A P,Bastviken D,et al.Methane fluxes show consistent temperature dependence across microbial to ecosystem scales[J].Nature,2013,507(7493): 488–491

[3]von Caemmerer S,Farquhar G D.Some relationships between the biochemistry of photosynthesis and the gas exchange of leaves[J].Planta,1981,153(4):376–387

[4]Harley P C,Sharkey T D.An improved model of C3photosynthesis at high CO2:Reversed O2sensitivity explained by lack of glycerate reentry into the chloroplast[J]. Photosynthesis Research,1991,27(3):169–178

[5]Bernacchi C J,Singsaas E L,Pimentel C,et al.Improved temperature response functions for models of Rubisco-limited photosynthesis[J].Plant,Cell&Environment,2001,24(2): 253–259

[6]Long S P,Bernacchi C J.Gas exchange measurements,what can they tellus aboutthe underlying limitations to photosynthesis?Procedures and sources of error[J].Journal of Experimental Botany,2003,54(392):2393–2401

[7]Sharkey T D,Bernacchi A J,Farquhar G D,et al.Fitting photosynthetic carbon dioxide response curves for C3leaves[J].Plant,Cell&Environment,2007,30(9):1035–1040

[8]Harley P C,Thomas R B,Reynolds J F,et al.Modelling photosynthesis of cotton grown in elevated CO2[J].Plant,Cell &Environment,1992,15(3):271–282

[9]Wullschleger S D. Biochemical limitations to carbon assimilation in C3plants— A retrospective analysis of theA/Cicurves from 109 species[J].Journal of Experimental Botany,1993,44(5):907–920

[10]Dubois J J B,Fiscus E L,Booker F L,et al.Optimizing the statistical estimation of the parameters of the Farquhar-von Caemmerer-Berry model of photosynthesis[J]. New Phytologist,2007,176(2):402–414

[11]Miao Z W,Xu M,Lathrop J R,et al.Comparison of the A-Cc curve fitting methodsin determining maximum ribulose 1.5-bisphosphate carboxylase/oxygenase carboxylation rate, potential light saturated electron transport rate and leaf dark respiration[J].Plant,Cell& Environment,2009,32(2): 109–122

[12]Su Y H,Zhu G F,Miao Z W,et al.Estimation of parameters of a biochemically based model of photosynthesis using a genetic algorithm[J].Plant,Cell&Environment,2009,32(12): 1710–1723

[13]Zhu G F,Li X,Su Y H,et al.Seasonal fluctuations and temperature dependence in photosynthetic parameters and stomatal conductance at the leaf scale ofPopulus euphraticaOliv[J].Tree Physiology,2010,31(2):178–195

[14]Feng X H,Dietze M.Scale dependence in the effects of leafecophysiological traits on photosynthesis: Bayesian parameterization of photosynthesis models[J]. New Phytologist,2013,200(4):1132–1144

[15]白岩,朱高峰,张琨,等.基于树干液流及涡动相关技术的葡萄冠层蒸腾及蒸散发特征研究[J].生态学报,2015, 35(23):7821–7831 Bai Y,Zhu G F,Zhang K,et al.Research of transpiration and evapotranspiration from a grapevine canopy combining the sap flow and eddy covariance techniques[J].Acta Ecologica Sinica,2015,35(23):7821–7831

[16]Ethier G J,Livingston N J.On the need to incorporate sensitivity to CO2transfer conductance into the Farquhar-von Caemmerer-berry leaf photosynthesis model[J].Plant,Cell& Environment,2004,27(2):137–153

[17]Bayes T.An essay towards solving a problem in the doctrine of chances,by the late Rev.Mr.Bayes,F.R.S.Communicated by Mr.Price,in a letter to John Canton,A.M and F.R.S[J]. Philosophical Transactions of the Royal Society of London, 1763,53:370–418

[18]Metropolis N R,Rosenbluth A W,Rosenbluth M N,et al. Equation of state calculations by fast computing machines[J]. Journal of Chemical Physics,1953,21(6):1087–1091

[19]Hastings W K.Monte Carlo sampling methods using Markov chains and their applications[J].Biometrika,1970,57(1):97–109 [20]Liu J S,Liang F M,Wong W H.The multiple-try method and local optimization in metropolis sampling[J].Journal of the American Statistical Association, 2000, 449(95): 121–134

[21]Zhu G F,Li X,Su Y H,et al.Simultaneously assimilating multivariate data sets into the two-source evapotranspiration model by Bayesian approach:Application to spring maize in an arid region of northwestern China[J].Geoscientific Model Development,2014,7(4):1467–1482

[22]EvansJR,Seemann JR.Differencesbetween wheat genotypes in specific activity of ribulose-1,5-bisphosphate carboxylase and the relationship to photosynthesis[J].Plant Physiology,1984,74(4):759–765

[23]刘涛,鲁剑巍,任涛,等.不同氮水平下冬油菜光合氮利用效率与光合器官氮分配的关系[J].植物营养与肥料学报, 2016,22(2):518–524 Liu T,Lu JW,Ren T,etal.Relationship between photosynthetic nitrogen use efficiency and nitrogen allocation in photosynthetic apparatus of winter oilseed rape under different nitrogen levels[J].Journal of Plant Nutrition and Fertilizer,2016,22(2):518–524

[24]Regina I S,Leonardi S,Rapp M.Foliar nutrient dynamics and nutrient-use efficiency inCastanea sativacoppice stands of southern Europe[J].Forestry,2001,74(1):1–10

[25]Wright I J,Reich P B,Westoby M.Least-cost input mixtures of water and nitrogen for photosynthesis[J].The American Naturalist,2003,161(1):98–111

[26]Adams M A,Turnbull T L,Sprent J I,et al.Legumes are different:Leafnitrogen,photosynthesis,and wateruse efficiency[J].Proceedings ofthe NationalAcademy of Sciences of the United States of America,2016,113(15): 4098–4103

[27]赵丽敏,李秧秧,左力翔.土壤渐进干旱过程中玉米、高粱茎水分传输能力与光合作用的协调性研究[J].中国生态农业学报,2013,21(7):817–823 Zhao L M,Li Y Y,Zuo L X.Coordination between stem water transport capacity and photosynthesis in corn and sorghum cultivars during progressive soil drying[J].Chinese Journal of Eco-Agriculture,2013,21(7):817–823

Biochemically-based model for photosynthetic parameter estimation using Bayesian method and its application in grapes in arid region*

ZHU Zhonghua1,HAN Tuo2**,LIU Jinquan3,ZHU Gaofeng2
(1.Gansu Provincial Water Conservancy and Hydropower School,Lanzhou 730021,China;2.College of Earth and Environmental Sciences,Lanzhou University/Key Laboratory of Environmental Systems of Western China of Ministry of Education,Lanzhou 730000,China;3.Huating County Water Authority,Huating 744100,China)

The response of photosynthesis to CO2concentration can provide a number of important parameters related to environmental factors.Using white seedless grape as the tested material in this study,net photosynthetic rates of leaves were measured for different intercellular CO2concentrations during two typical growing seasons from June to September in 2014and 2015.A widely used biochemical model(FvCB model)in the simulation of CO2and H2O gas exchange at the leaf scale was parameterized using data obtained from situ leaf-scale observations.In order to obtain the photosynthetic parameters values,to explore seasonal variations in the photosynthetic parameters in different seasons and to discuss the feasibility and advantage of the Bayesian method in solving high dimensional and complex model parameters estimation,the Bayesian approach was used to estimate the parameters of the FvCB model.In order to generate the Bayesian posterior probability distribution,a version of the Markov Chain Monte Carlo(MCMC)technique was used.In contrast,the least square procedure was used in the application of the same set of observational data.The results showed that maximum ribulose 1.5-bisphosphate carboxylase/oxygenase(Rubisco)carboxylation rate(Vcmax),potential light-saturated electron transport rate(Jmax)and the rate of use of triose-phosphates utilization(TPU)had evident seasonal variations which increased from June to August,and then decreased in September.The maximum values were observed in August(54.30µmol∙m-2∙s-1,88.45µmol∙m-2∙s-1and 6.56µmol∙m-2∙s-1, respectively)and minimum values in September(34.66µmol∙m-2∙s-1,58.86µmol∙m-2∙s-1and 4.38µmol∙m-2∙s-1,respectively).The trend in mesophyll conductance(gm)was relatively stable in different months,with respective values of 5.16µmol∙m-2∙s-1∙Pa-1,5.29 µmol∙m-2∙s-1∙Pa-1,5.39µmol∙m-2∙s-1∙Pa-1,5.41µmol∙m-2∙s-1∙Pa-1from June to September.In comparison with traditional least square method,the values ofVcmaxestimated by the Bayesian method were relatively small and those ofJmax,TPU andgmhad no obvious difference.Also because the estimated parameters by the Bayesian method were obtained after adequate consideration of prior information,each parameter was in biological sense obviously more meaning.As a consequence,it indicated that the Bayesian approach combined with Markov Chains and Monte Carlo(MCMC)sampling algorithm was an effective way of estimation of the parameters in the FvCB model.As the parameters in the FvCB model were different in different seasons,it was necessary to consider these variations in using the parameters in the FvCB model.

Arid region;Grape;Bayesian parameter estimation;Biochemical photosynthesis model;Photosynthetic parameter; Seasonal variation

Oct.29,2016;accepted Mar.1,2017

Q945.79

A

1671-3990(2017)06-0876-08

10.13930/j.cnki.cjea.160967

朱中华,韩拓,柳金权,朱高峰.基于贝叶斯方法的光合作用生化模型参数估计及其在干旱区葡萄上的应用[J].中国生态农业学报,2017,25(6):876-883

Zhu Z H,Han T,Liu J Q,Zhu G F.Biochemically-based model for photosynthetic parameter estimation using Bayesian method and its application in grapes in arid region[J].Chinese Journal of Eco-Agriculture,2017,25(6):876-883

* 国家自然科学基金(41571016)和中央高校基本科研业务费(861944)资助

**通讯作者:韩拓,主要从事生态水文方面的研究。E-mail:hant14@lzu.edu.cn

朱中华,主要研究方向为水利水电和生态水文。E-mail:hant16@lzu.edu.cn

2016-10-29 接受日期:2017-03-01

* This study was supported by the National Natural Science Foundation of China(41571016)and the National Higher-education Institution General Research and Development Project of China(861944).

**Corresponding author,E-mail:hant14@lzu.edu.cn