星间差伪距/伪距率BDS/GPS/INS紧组合系统

孟凡效，孙红星，丁学文

(1.武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079； 2.中国兵器工业集团 北方信息控制集团有限公司，南京 211100)



星间差伪距/伪距率BDS/GPS/INS紧组合系统

孟凡效1，孙红星1，丁学文2

(1.武汉大学 测绘遥感信息工程国家重点实验室，武汉 430079； 2.中国兵器工业集团 北方信息控制集团有限公司，南京 211100)

针对GPS/INS紧组合定位定姿中GPS单模系统抗干扰性差和安全性低的问题，提出在不改变GPS/INS组合定位方程的前提下，利用BDS/GPS/INS多模组合的方式提高系统的可用观测量，使用星间差分的方式消除接收机钟差、钟差漂移等效距离误差的方法，不仅可以省去对上述误差进行建模，还能有效增加组合滤波器的稳定性，提高组合系统连续工作的能力。然后根据已有BDS/GPS单点定位测速理论，推导出星间差伪距/伪距率实时紧组合量测更新方程。实验结果表明，此方法能够较好提高组合系统的稳定性和持续工作能力。

BDS；GPS；INS；伪距/伪距率；星间差；实时紧组合

0 引言

全球卫星导航系统(global navigation satellite system，GNSS)和惯性导航系统(inertial navigation system，INS)进行组合导航，可充分发挥各自系统的优势，进而互补，实现高动态、高精度的定位[1]。目前组合导航系统根据信息交换程度或滤波结构主要分为3种模式：松耦合、紧耦合和超紧耦合[2]。对于紧组合而言，研究全球定位系统(global positioning system，GPS)和INS紧组合的文献较多[3-7]，大多都是通过仿真数据进行研究及算法验证；而对于中国北斗卫星导航系统(BeiDou navigation satellite system，BDS)和INS紧组合的研究文献相对较少[9-12]，因此对于BDS/GPS/INS实时紧组合的研究就更加必要。

随着BDS的逐步建成，我国已于2016-06-12发射了第23颗BDS导航卫星,因此对于卫星的使用将更加倾向于我国自主研发的BDS。本文提出一种基于星间差伪距/伪距率的BDS/GPS/INS实时紧组合观测模型，将BDS与GPS数据进行统一处理，与INS实现实时紧组合，即使在GPS受限时BDS/INS仍可继续工作。

1 星间差实时紧组合系统状态方程

星间差紧组合状态方程包含INS和BDS/GPS 2部分，BDS/GPS状态向量中存在的接收机钟差、钟差漂移等效距离误差等使用星间差算法可以消除，从而减少对该误差项的建模等工作，故BDS/GPS/INS状态方程可写为

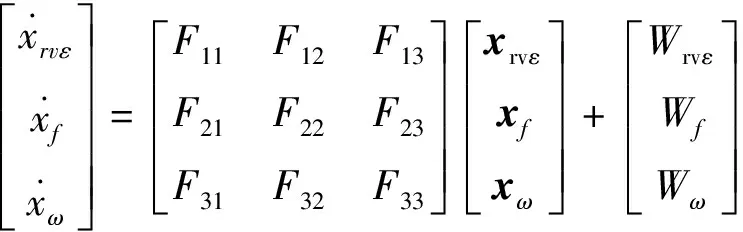
(1)

可将式(1)简写为

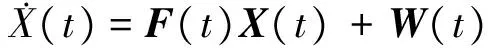
(2)

式中：X(t)=[xrvεxfxω]T=[δX δY δZ δVXδVYδVZεXεYεZfXfYfZωXωYωZ]T。其中：X(t)是15阶的状态向量；xrvε=[δRδVδE]是INS9阶导航误差向量，包含位置、速度、姿态误差，δR=[δXδYδZ]表示在地固坐标系的X、Y、Z 3个方向的位置误差矢量，δV=[δVXδVYδVZ]表示地固坐标系的X、Y、Z 3个方向的速度误差矢量，δE=[εXεYεZ]表示载体平台失准角误差矢量；xf=[fXfYfZ]表示加速度计3轴零偏误差矢量；xω=[ωXωYωZ]表示陀螺3轴零偏误差矢量。F(t)代表状态方程的动态矩阵，是一个15维的稀疏矩阵，具体各元素可参见文献[1]的附录；W(t)=[WrvεWfWω]T为噪声矩阵，具体可参见文献[13]。

2 实时紧组合系统量测方程

2.1 基于伪距的量测方程

对于BDS/GPS观测方程可列为

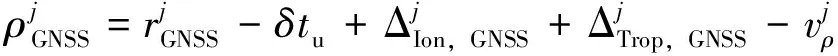
(3)

对于INS观测方程(一阶泰勒展开式)，可表示为

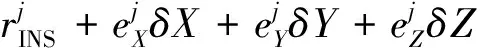
(4)

将式(3)与式(4)做差可得

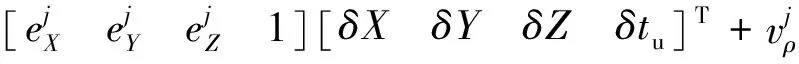
(5)

式(5)即为基于BDS/GPS/INS伪距的紧组合量测更新观测方程。

2.2 基于伪距率的量测方程

BDS/GPS的伪距率观测方程即如对式(3)方程两边求导得

(6)

式(6)可整理得

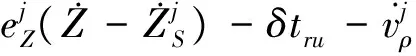
(7)

INS的伪距率观测方程即为对式(4)方程进行两边求导得

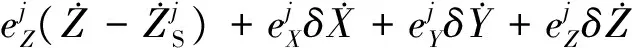
(8)

将式(7)与式(8)进行做差，整理得

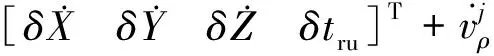
(9)

式(9)即为基于BDS/GPS/INS伪距率的紧组合量测更新观测方程。

2.3 基于星间差的伪距/伪距率量测方程

本文研究的实时紧组合算法关注的是载体的姿态、速度和位置，状态向量中惯性测量单元(inertialmeasurementunit，IMU)传感器误差和接收机钟差、钟差漂移等效距离误差不是本文的研究重点；另外由于受到BDS/GPS信号丢失、车辆的低速运动等条件影响，本身微小误差项的可观测性差，滤波器难以对其进行有效估计，并且可能降低系统的稳定性。鉴于以上2点原因，本文采用星间差方式消除接收机钟差和时钟漂移对应的等效距离误差，使得系统状态向量维数从19降低至15。

分别选择BDS、GPS卫星系统的高度角最大的一颗卫星作为各自系统的参考卫星，将其余卫星观测方程与该系统参考卫星的观测方程做差，即可得星间差量测方程。以BDS卫星为例，参考卫星为j，观测卫星为k，分别利用式(5)和式(9)做差后可得星间差量测方程为：

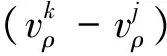
(10)

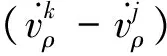
(11)

3 实验与结果分析

为了评估本文基于星间差伪距/伪距率的BDS/GPS/INS紧组合算法的有效性，进行车载户外跑车测试，并且利用VisualC++编写实时紧组合和事后松散组合定位定向软件，对采集的数据进行处理，验证星间差实时紧组合算法的可靠性。

3.1 系统组成及跑车实验

实验设备包含1套定位定姿系统(positioningandorientationsystem，POS)硬件部分和1台基站接收机，由武汉际上导航科技有限公司提供。POS硬件部分包含1台双星三频BDS/GPS接收机和1台国产某型号的战术级光纤IMU惯导设备，惯导数据采样率为200Hz，其精度指标可参见表1。接收机作为移动站与惯导设备一起安放在车顶采集数据，移动站数据采样率为5Hz。基站接收机安放在楼顶进行静态数据采集，采样率为1Hz，采集的数据在后处理时使用。图1给出了POS的安装结构以及配套的地面基站，POS天线安置在惯导中心的正上方。图2给出了实际跑车采集数据时POS在车顶的安装位置。

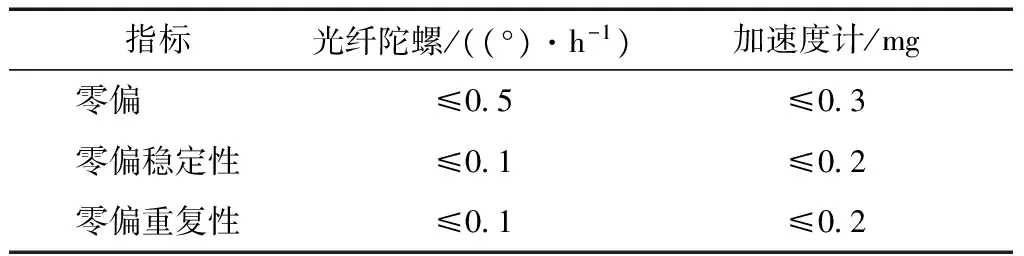
表1 战术级光纤IMU陀螺和加速度计主要精度指标

为了更全面地验证本文算法的有效性，本次试验选择2种不同观测条件的场地进行对比：一是围绕武汉大学校园观测，道路弯曲且卫星观测条件极其恶劣；二是选在武汉市江夏区的某工业园区内，道路平整且路段内卫星观测条件良好。数据采集时，将POS系统设备固定在测试车辆顶部；系统启动后先预热10 min左右，一方面使陀螺的性能达到最优状态，另一方面用于系统的姿态粗对准，随后在既定的轨迹道路上运动2遍。以此2组数据，从星间差BDS/GPS/INS与非星间差BDS/GPS/INS实时紧组合、松组合2个方面展开分析对比(如表2所示)。

表2 2组试验采集数据移动站基本情况

3.2 星间差与非星间差BDS/GPS/INS实时紧组合结果对比

为了验证该算法的有效性，分别按照星间差和非星间差伪距/伪距率的BDS/GPS/INS紧组合算法处理跑车采集的2组数据，以事后差分松组合结果作为基准，对比星间差紧组合及非星间差紧组合结果(如图3、图4所示)。

由图可以看出，使用星间差分算法计算的结果与基准结果更加吻合，而非星间差的实时紧组合吻合程度不是很好，尤其是在观测条件差的情况下，轨迹会出现较大的偏差，这是由于：BDS/GPS在恶劣观测条件下，有效观测条件方程数目较少，使得高维度的滤波器状态方程容易发散，进而难以对紧组合中各项状态向量进行有效估计；而使用星间差的算法可以降低滤波器状态的维度，从不使用星间差紧组合的19维状态向量降至15维的状态向量，在观测条件方程较少时由于此算法滤波器的维数较低，仍可以对状态向量进行有效估计，从而体现出基于星间差的伪距/伪距率BDS/GPS/INS实时紧组合算法的有效性及优越性。

3.3 星间差BDS/GPS/INS实时紧组合与松组合对比分析

为得到基于星间差伪距/伪距率的BDS/GPS/INS实时紧组合算法的精度，对2组跑车采集数据分别按照仅使用伪距紧组合和使用伪距/伪距率紧组合进行处理，并把结果与基准结果做差进行对比，进一步分析使用伪距率这一观测量对定位精度所起的作用。

图5为第1组跑车数据伪距紧组合、伪距/伪距率紧组合、基准(松组合)结果的轨迹对比，通过图5可以发现，在使用伪距观测量的基础上，增加伪距率这一观测量，使得基于星间差实时紧组合算法得到的点位精度有一定的提升，特别是在卫星颗数少于4颗时效果更明显，这是由于增加伪距率这一观测量后，使得观测条件方程增加到定位所需要的方程数所导致。

图6～图8、表3为第1组伪距紧组合、伪距/伪距率紧组合和基准的东向、北向及天向位置差值对比情况。

可以看出，在BDS/GPS恶劣观测条件下，基于星间差的伪距/伪距率实时紧组合的点位精度要优于星间差伪距实时紧组合，从东向、北向、天向的位置误差均值可以得出：使用伪距/伪距率的紧组合算法能够比仅使用伪距的紧组合算法的定位精度提升1～2 m，这是由于增加伪距率这一观测量，就可以有更多的观测方程，达到了定位所需的观测方程数目。

图9为第2组跑车数据伪距紧组合、伪距/伪距率紧组合、基准结果的轨迹对比。

通过图9可以发现，在BDS/GPS卫星观测良好条件下，在使用伪距观测量的基础上，增加伪距率这一观测量，使得基于星间差的实时紧组合算法得到的点位结果精度的提升不很明显，这是由于在增加伪距率这一观测量之前，卫星条件方程数目已经达到所需个数，继续增加观测条件方程不会对结果有太大影响。

表3 第1组东向、北向、天向位置差值统计 m

图10～图12、表4为第2组伪距紧组合、伪距/伪距率紧组合和基准的东向、北向及天向位置差值对比情况。

在图12中，天向位置误差在观测时间1 600 s时出现跳变是由于卫星分布以及可见卫星颗数发生变化导致的，而且该变化使得天向的位置定位精度有所提升，从开始的10 m左右误差降到了5 m以内。

可以看出，在BDS/GPS观测良好的情况下，基于星间差伪距/伪距率的实时紧组合和基于星间差的伪距实时紧组合的点位定位精度相较BDS/GPS观测恶劣条件下有明显的提升，从之前100 m左右的最大误差降低至10 m左右。从东向、北向以及天向的位置误差均值来看，东向、北向误差均值从之前8 m左右降低至3 m左右，天向误差均值也由之前8 m左右降低至7 m左右。

在BDS/GPS观测良好的条件下，基于星间差伪距/伪距率实时紧组合比基于星间差伪距实时紧组合的点位精度从误差的均值来看有dm级的提升，北向和东向的误差最大值有1～2 m的提升；但是天向误差最大值稍差，这是由于在观测过程中可见卫星数量以及分布发生变化导致的。从均值和标准差来看2种算法的差别不是很大，这是由于该系统已经存在足够多的观测信息，增加伪距率的约束条件达到一定数量时对于组合系统的精度提升有限。

图13～图15、表5为第2组伪距紧组合、伪距/伪距率紧组合和基准的东向、北向及天向速度差值的对比情况。

表4 第2组东向、北向、天向位置差值统计 m

可以看出，在BDS/GPS观测良好的条件下，基于星间差伪距/伪距率的BDS/GPS/INS实时紧组合比基于星间差伪距的BDS/GPS/INS实时紧组合的速度精度有一定的提升。东向、北向的速度差值较天向的速度差值有明显的提升，这是由于车辆运动过程中在东向、北向出现较大的变化，而在平坦道路中行驶天向变化较小。2种算法的速度精度相当也是由于观测良好条件下，系统已经有足够多的观测信息，再增加伪距率这一信息，条件方程数量的增加起到的作用也会有一定的限制，并非无限提升。

表5 第2组东向、北向、天向速度差值统计 m/s

4 结束语

本文通过实际跑车数据对基于星间差的伪距/伪距率的BDS/GPS/INS实时紧组合模型算法进行验证，将BDS与GPS统一与INS组成实时紧组合，并按照BDS/GPS观测条件的优劣进行2组跑车试验。与不使用星间差的算法进行对比，既能够验证星间差算法的有效性，又可以减少对钟差的建模工作量。实时星间差紧组合算法能够在卫星少于4颗的恶劣环境下正常工作，并且提供连续的导航信息服务。在BDS/GPS观测条件恶劣的情况下，使用星间差伪距/伪距率的实时紧组合的位置精度可以比仅使用星间差伪距进行紧组合的位置精度提高1～2 m，而在BDS/GPS观测条件较好的条件下，使用星间差伪距/伪距率的实时紧组合的位置精度比仅使用星间差伪距进行紧组合的位置精度有dm级的提高。良好环境下的实时紧组合和事后松组合(基准)的对比试验结果表明，基于星间差伪距/伪距率的BDS/GPS/INS实时紧组合算法可以提供精度在10 m以内的位置服务及m级以内的实时测速服务。

[1] 董绪荣,张守信,华仲春.GPS/INS 组合导航定位及其应用[M].长沙:国防科技大学出版社,1998:339-342.

[2] 陈偲,王可东.惯性导航与卫星导航紧耦合技术发展现状[J].全球定位系统, 2007, 2007(3):21-26.

[3] 臧中原.基于伪距/伪距率的SINS/GPS紧组合导航系统研究[D].北京：北京理工大学, 2015:2-7.

[4] 鲁郁, 胡锐, 杨云春. 一种低成本GPS/INS紧耦合组合导航系统[J]. 武汉大学学报(信息科学版), 2011, 36(4):481-485.

[5] 周星伶. GPS/INS组合导航系统松、紧耦合性能比较[J]. 航空电子技术, 2007, 38(4):1-6.

[6] 周坤芳, 孔键, 周湘蓉. 紧耦合GPS/INS组合导航能力的分析[J]. 中国惯性技术学报, 2005, 13(6):51-53.

[7] 高娟, 韩惠珍, 白军. SINS/GPS紧耦合与松耦合组合导航系统分析[J]. 四川兵工学报, 2011, 32(10):92-96.

[8] 袁俊刚. GPS/惯性紧组合导航系统研究[D]. 南京：南京航空航天大学, 2011:15-20.

[9] 薛东, 黄国荣, 彭兴钊, 等. SINS/GPS/BDS紧耦合系统研究[J]. 计算机测量与控制, 2012, 20(9):2567-2570,2573.

[10]董淼, 宋艳君, 夏奇, 等. BDS/SINS紧耦合组合导航技术仿真研究[J]. 计算机仿真, 2014, 31(8):97-100.

[11]孙红星. 差分GPS/INS组合定位定姿及其在MMS中的应用[D]. 武汉：武汉大学, 2004:53-60.

[12]李靖松. 基于伪距/伪距率组合导航技术的研究[D]. 南京：南京理工大学, 2009:67-74.

[13]黎蕾蕾, 孙红星, 李德仁, 等. 车载移动测量中定位定姿系统误差校正与补偿研究[J]. 武汉大学学报(信息科学版), 2016,41(9):1245-1252.

BDS/GPS/INS tight-coupling system using differential pseudo-range and pseudo-range rate between satellites

MENGFanxiao1,SUNHongxing1,DINGXuewen2

(1.State Key Laboratory of Information Engineering in Surveying,Mapping and Remote Sensing,Wuhan University, Wuhan 430079, China;2.North Information Control Group Co.Ltd., China North Industries Group Corporation, Nanjing 211100, China)

Aiming at the problem that there is poor anti-interference ability and low security of GPS single-mode system in the positioning and orientation determination of GPS/INS tight-coupling system, the paper proposed a method that uses BDS/GPS/INS multi-mode combination to improve the usable observations of system, without changing the GPS/INS integrated positioning equation, and eliminated the clock error of the receiver and the equivalent range error of the clock error drift with the differential observations between satellites.The method could help not only avoid modeling for those errors, but also effectively increase the stability of the junction filter, and improve the continuous working ability of the system.Moreover, the updating equations of the real-time tight-coupling system of differential pseudo-range and pseudo-range rate between satellites were deduced based on existing velocity measurement theory of BDS/GPS single point positioning.Experimental result showed that this method could improve the stability and continuous working ability of the combined system.

BDS; GPS; INS; pseudo range/pseudo-range rate; difference between satellites; real-time tight-coupling

2016-08-05

孟凡效(1990—)，男，山东济宁人，硕士研究生，研究方向为GNSS/INS组合导航定位。

国家测绘地理信息公益性行业科研专项项目(201412015)。

孟凡效，孙红星，丁学文.星间差伪距/伪距率BDS/GPS/INS紧组合系统[J].导航定位学报,2017,5(2):86-92.(MENG Fanxiao, SUN Hongxing, DING Xuewen.BDS/GPS/INS tight-coupling system using differential pseudo-range and pseudo-range rate between satellites[J].Journal of Navigation and Positioning,2017,5(2):86-92.)

10.16547/j.cnki.10-1096.20170215.

P228.4

A

2095-4999(2017)02-0086-07