基于SPH方法粒子射流破岩数值模拟与实验研究*

赵 健，张贵才，徐依吉，周 毅，王瑞英，邢雪阳，李建波

(1.中国石油大学(华东)石油工程学院,山东 青岛 266580；2.中国石油大学(华东)科学技术研究院，山东 东营 257061；3.中海油能源发展股份有限公司安全环保分公司，天津 300450)

基于SPH方法粒子射流破岩数值模拟与实验研究*

赵 健1,2，张贵才1,2，徐依吉1，周 毅1，王瑞英1，邢雪阳1，李建波3

(1.中国石油大学(华东)石油工程学院,山东 青岛 266580；2.中国石油大学(华东)科学技术研究院，山东 东营 257061；3.中海油能源发展股份有限公司安全环保分公司，天津 300450)

钻井液中加入体积分数为1%～3%的钢质粒子在钻头喷嘴处高速喷出冲击岩石，实现了粒子射流冲击和钻头机械联合破岩，有效提高了破岩效率。利用瞬态非线性动力学有限元模拟软件，基于光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法，考虑流体对粒子射流冲击的影响，建立了粒子射流冲击破岩的物理模型，获得了粒子射流参数对破岩体积的影响规律，进行了室内实验验证，验证了SPH方法的有效性。结果表明：粒子射流冲击岩石表面形成规则的V型冲击坑；同条件下粒子射流破岩体积是水射流破岩体积的2～4倍；随着粒子射流冲蚀时间的增加，粒子射流破岩体积不断增加，但破岩效率降低；粒子射流压力大于10 MPa后，粒子射流破岩效率迅速增大；喷射角度大于6°后，破岩效率迅速减小。

粒子射流；冲击破岩；SPH方法；室内实验

粒子冲击钻井技术可以有效提高深井硬地层钻井速度，通过井下钻头喷嘴喷出的高频、高速钢质粒子冲击岩石，粒子冲击时间极短，接触面积极小，产生的瞬时接触应力极大，改变了常规钻头的破岩方式，极大提高了能量利用率[1-4]。徐依吉等[5-6]分析得出粒子冲击破岩过程是涉及多因素的非线性冲击动力学问题，在粒子冲击过程中产生的瞬时动载荷大、变形大、冲击作用时间短。S.M.Wiederhorn等[7]、G.L.Sheldon[8]、A.G.Evans等[9]研究发现粒子冲击岩石能够产生裂纹需要最小的临界速度，影响岩石冲蚀磨损速率的主要参数为粒子冲击速度，冲蚀磨损速率可用冲击速度的幂函数来表示。T.A.Adler等[10]得出冲击磨损量与冲击过程中产生的赫兹接触应力的值关系较大。J.Wang等[11]通过钢球冲击白口铸铁破碎坑体积计算，得到了磨料切割深度和磨料弹性能量之间的比例关系。 王明波等[12]、况春雨等[13]得出磨料水射流破岩的主要形式是磨料颗粒冲击产生的压力波所导致的岩石拉伸破坏。姜美旭等[14]利用ANSYS隐式-显式序列求解方法，研究了围压对粒子冲击岩石损伤的影响。伍开松等[15]运用一维应力波理论分析了粒子冲击破岩现象，采用IDFEM软件研究了粒子冲击破岩规律。综上所述，已开展的粒子冲击破岩研究，均为单个或者几个粒子冲击破岩数值模拟，没有考虑射流的加入对粒子冲击破岩的影响，数值模拟条件和实际条件差别较大，同时单粒子冲击破岩和实际钻井粒子射流破岩条件差别较大。本文中，针对如何提高粒子冲击效率的问题，基于光滑粒子流体动力学(smoothed particle hydrodynamics，SPH)方法，开展射流条件下粒子冲击破岩的数值模拟和实验研究，以期研究结果为粒子冲击技术现场实验提供理论指导。

1 基于SPH方法粒子射流破岩有限元模型

利用SPH方法建立粒子射流模型，采用有限元方法(finite element method,FEM)对岩石进行建模并划分网格,假设：(1)整个粒子射流破岩过程中，只涉及粒子、水、岩石3种物质；(2)粒子为直径相等的圆球体；(3)粒子在水中随机分布；(4)粒子为刚性粒子不发生损伤和变形;(5)岩石裂纹、空隙、胶结等 不影响粒子射流破岩，岩石为连续介质。

1.1 SPH粒子射流模型

对粒子与水采用SPH算法建模。在SPH 中任一宏观变量都能方便地借助于一组无序点上的值表示成积分插值计算得到。核近似函数[16]为：

(1)

式中:f(x)为三维坐标向量x的函数；Ω为点x的支持域；x-x′为粒子间距离；h为SPH粒子的光滑长度，光滑长度随时间和空间变化；W(x-x′,h)为核函数，通常使用辅助函数θ(x-x′)定义：

(2)

式中：d为空间维数。用粒子近似方法将连续形式积分方程换算成离散形式的方程，即：

(3)

式中：ρi为粒子i的密度；mi为粒子i的质量。

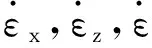
(4)

(5)

(6)

(7)

(8)

(9)

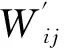
(10)

从上述方程中求得应变率、角加速度、体积应变后，可以求得粒子的正应力偏量、剪切力偏量、压力及标准状态下的人工黏度等。粒子为钢粒,其密度为7 800 kg/m3,弹性模量为202 GPa,泊松比为0.3。

对水采用MAT_NULL流体空模型，本构关系方程采用Mie-Grüneisen状态方程：

(11)

式中：E为体积内能；c为us-up曲线截距；S1、S2和S3为曲线斜率系数；γ0为Mie-Grüneisen常数；a为体积修正量。

水的参数[17]为：ρ0=1 g/cm3，c=1 480 m/s,S1=2.56,S2=-1.986,S3=0.228 6,a=1.397,γ0=0.49。

1.2 HJC岩石损伤模型

Holmquist-Johnson-Cook(HJC)模型中综合考虑了岩石材料损伤、应变率以及静水压力对屈服力的影响，是一种常用的岩石在大应变、高应变率、高压下的岩石损伤模型[18]。HJC模型的屈服面方程：

(12)

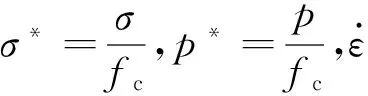
损伤因子通过等效塑性应变和塑性体积应变累计得到[19]：

(13)

式中：D为损伤度；Δεp和Δμp分别为一个计算循环内的等效塑性应变和塑性体积应变；D1、D2为材料常数；T*=T/fc，T为材料的最大拉伸强度。

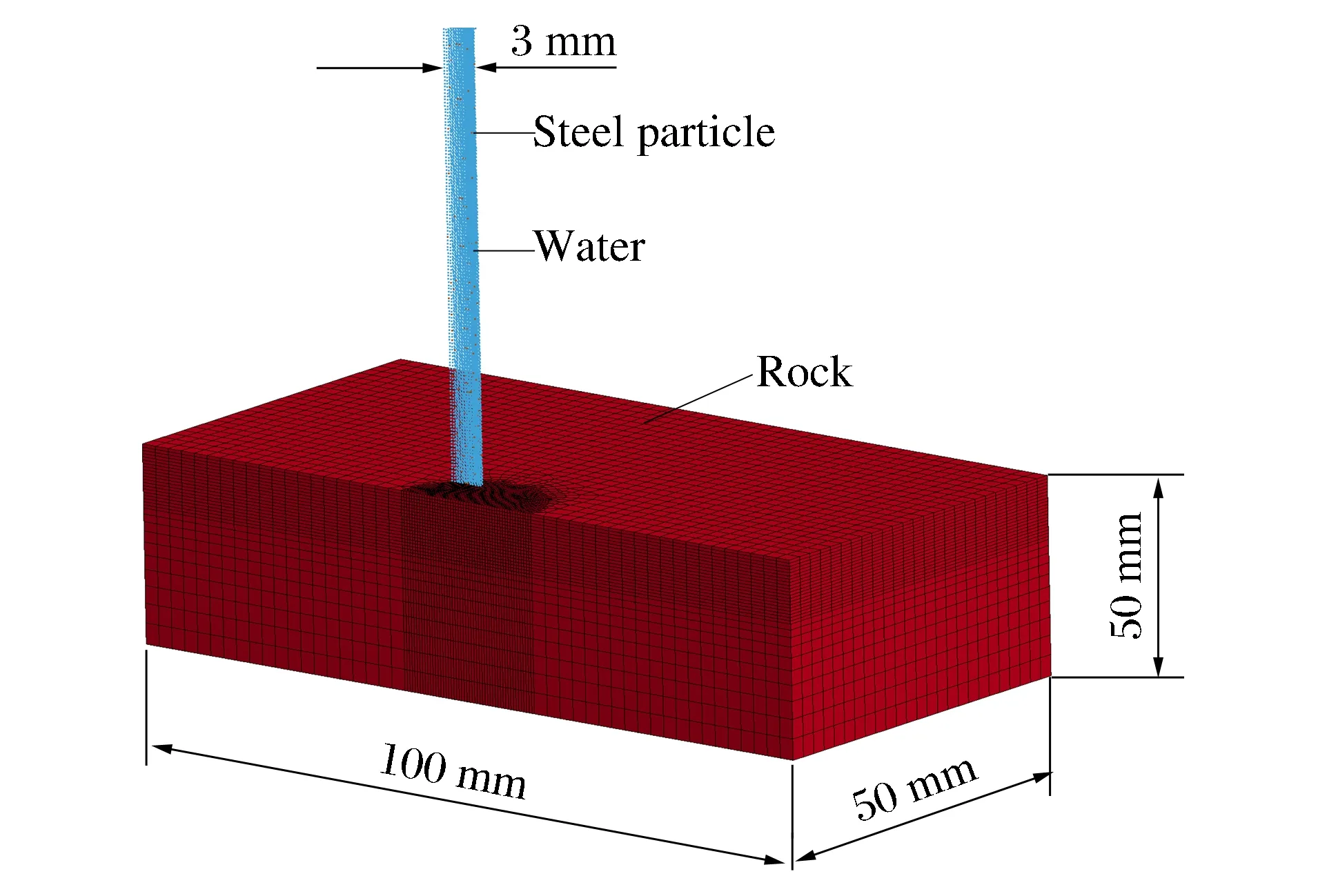
图1 粒子射流破岩计算模型Fig.1 Calculation model for rock breaking caused by particle jet

1.3 模型建立及网格划分

岩石为立方体，采用映射网格划分法，底面和侧面采用非反射约束；SPH粒子和岩石之间采用节点与面类型接触。水粒子SPH模型完成后，在k文件中随机选取设计浓度的水粒子将其属性改为钢球粒子，实现钢粒和水之间的混合。粒子射流破岩计算模型及几何尺寸如图1所示，红色标记为钢质粒子。

2 粒子射流冲击破岩实验

2.1 实验设备及实验流程

实验设备如图2所示，主要包括高压泵、实验架、泥浆罐、高压管线、加料漏斗、射流喷嘴等，高压泵最高压力为150 MPa，最大排量为60 L/min。

实验流程如图3所示，选用后混式粒子注入方式[20]：开启进水阀门，启动高压泵，水流从水箱进入高压泵加压，通过高压管线输送到后混式粒子混合仓，粒子在负压作用下与高压水流混合，并通过射流喷嘴喷出冲击岩石。

图2 粒子射流破岩实验设备Fig.2 Experimental equipment of rock breaking with particle jet

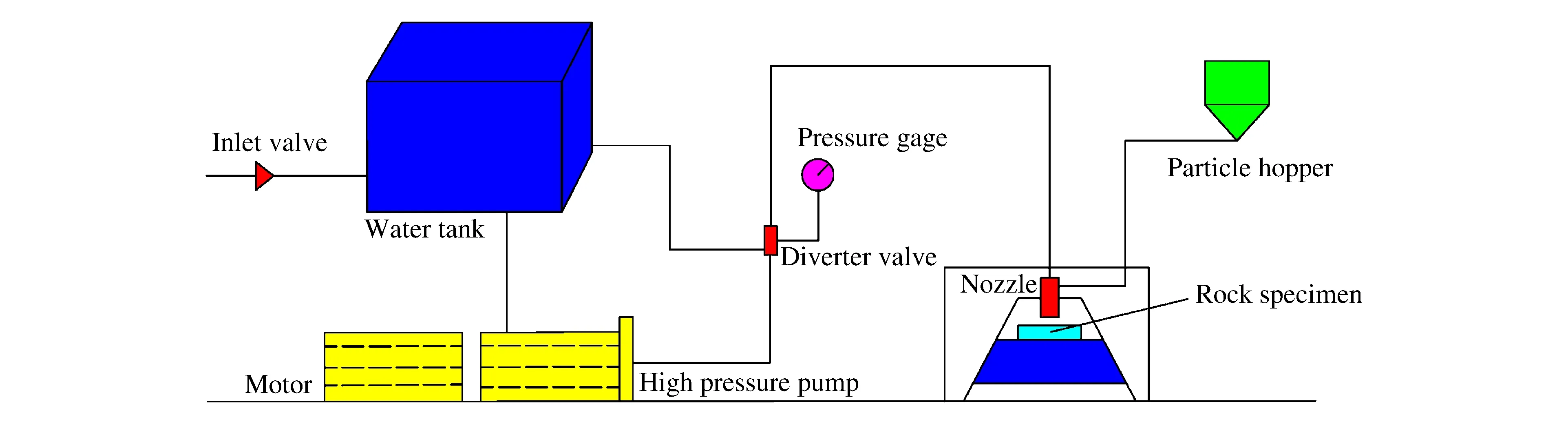
图3 粒子射流破岩实验流程Fig.3 Flow diagram of rock breaking with particle jet

2.2 样品

粒子选用球型硬质粒子，粒子密度为7.8 g/cm3；岩石为大理石，密度为2.6～2.8 g/m3。实验用到的粒子和冲击后的岩样如图4所示。

图4 实验粒子及冲击后岩样Fig.4 Experimental particles and rock sample after impact

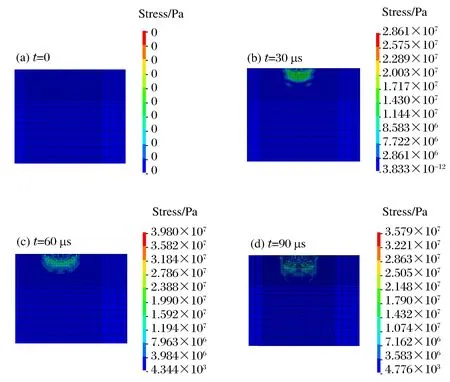
图5 岩石等效应力云图Fig.5 Von Mises stress nephogram of the rock

3 结果分析

3.1 粒子射流破岩分析

粒子在液相高速流体携带加速下，从喷嘴高速喷出，高速粒子和水射流共同冲击到岩面，粒子射流破岩为粒子冲击和水射流破岩的耦合作用过程；高速粒子接触岩石后，在接触面产生极大的瞬时接触应力，产生接触应力大大超过岩石的强度极限，岩石开始产生破碎，随着粒子的不断冲击，粒子射流冲蚀深度不断增大，冲击破碎坑的体积不断增大。由图5可知，粒子射流冲击岩石后，在接触面附近形成极大等效应力，等效应力最大值分布在破碎坑表面附近。

由图6可知：数值模拟和室内实验结果均表明，粒子射流冲击破岩之后，会在岩石表面形成一个V型冲击坑。由于在粒子射流横截面上，喷嘴中心轴线上粒子速度最大，喷嘴中心轴线四周粒子速度逐渐降低，因此射流轴上粒子动能最大，冲击破碎岩石能量最大，因此喷嘴中心轴线上破岩深度最大；同时在粒子反弹和水射流对冲击坑的共同修整作用下，在岩石表面形成了规则的V型冲击坑。

图6 粒子射流形成的V型冲击坑Fig.6 V-shaped crater caused by particle jet

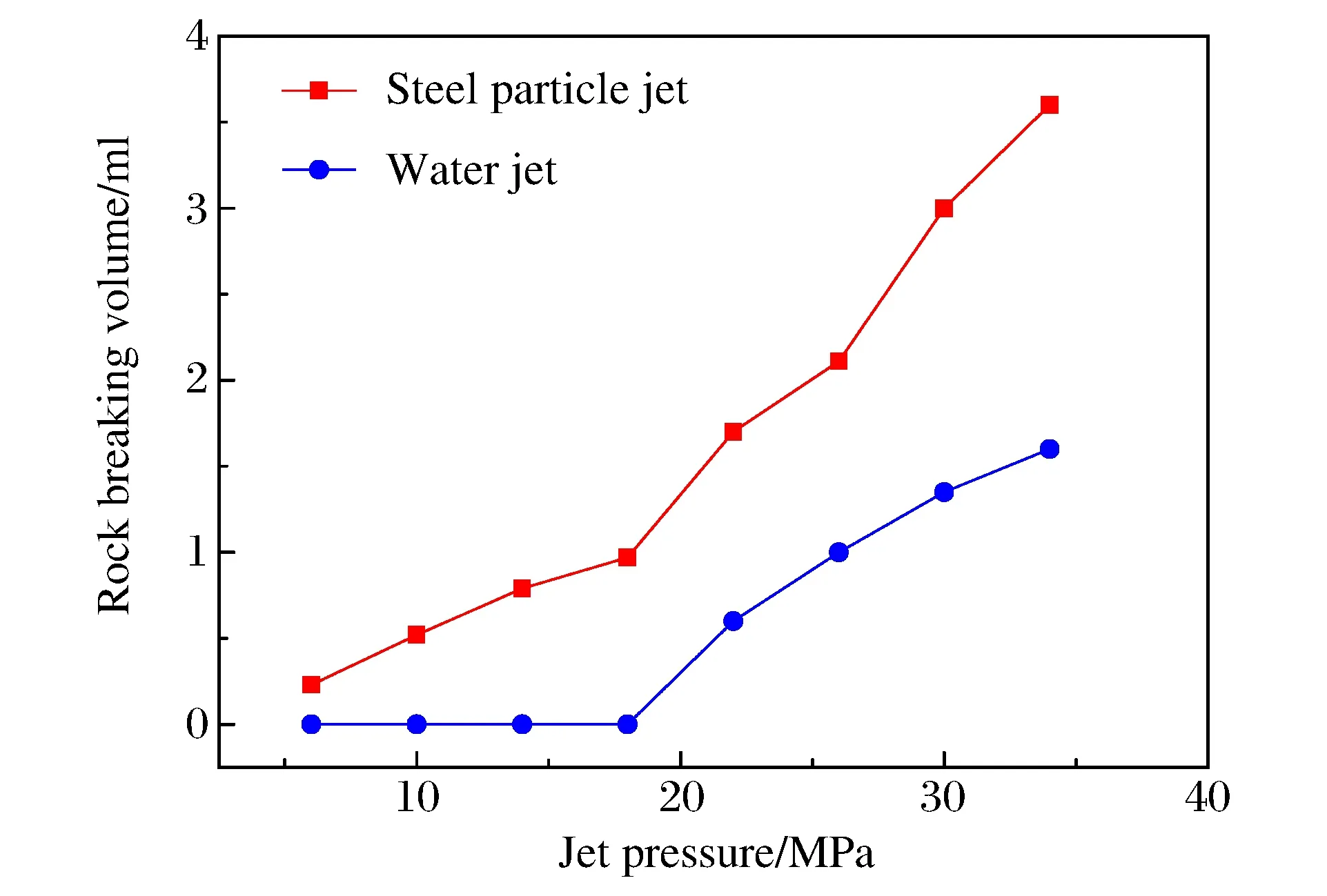
图7 粒子射流破岩和水射流破岩Fig.7 Rock breaking caused by particle jet and water jet

3.2 粒子射流和水射流破岩对比

由图7可知：粒子射流冲蚀时间为20 s，在相同的射流压力下，实验得出粒子射流破岩体积约为水射流破岩体积的2～4倍；粒子射流的破岩门限压力明显低于水射流破岩的门限压力。说明射流中加入粒子后，高速粒子冲击岩石，可以实现岩石的大体积破碎，有效提高射流的破岩效率，降低了岩石破碎的“门槛”，充分表明了粒子冲击在提高钻头破岩效率、增加钻井钻速方面的巨大优势。

3.3 时间对粒子射流破岩效果的影响

由图8可知：射流压力相同的条件下，随着粒子射流冲蚀时间的增加，粒子射流破岩体积不断增加。粒子射流不断冲蚀岩石，粒子冲击岩石后在极短接触时间内，形成极大的瞬时接触应力，岩石内部形成裂纹；粒子离开岩石而且不断有后续粒子冲击，岩石内部裂纹贯串形成大的体积破碎；破碎岩石在水射流作用下快速被携带出破碎区域；随着粒子射流的不断侵彻，形成的冲击坑体积不断增加，因此射流破岩体积不断增加。数值模拟和室内实验得到粒子射流破岩体积随时间的变化规律基本吻合。

随着时间的增加，图8中各曲线斜率呈下降趋势，说明冲蚀时间增加，单位时间内的粒子射流破岩体积减小，即破岩效率降低。由于随着冲蚀时间的增加，冲击坑体积不断增大，粒子射流达到岩石表面的运动距离增大，因此运动过程中的能量损耗增加；而且冲击坑体积增大，粒子射流在坑内的运动更复杂，射流的能量损耗增大，因此破岩效率会降低。为充分利用粒子射流能量，在实际钻井过程中，不仅需要粒子射流破岩作用，同时需要借助钻头旋转和切削齿机械破岩作用，避免粒子射流对同一位置的持续冲蚀，而导致破岩效率的下降。

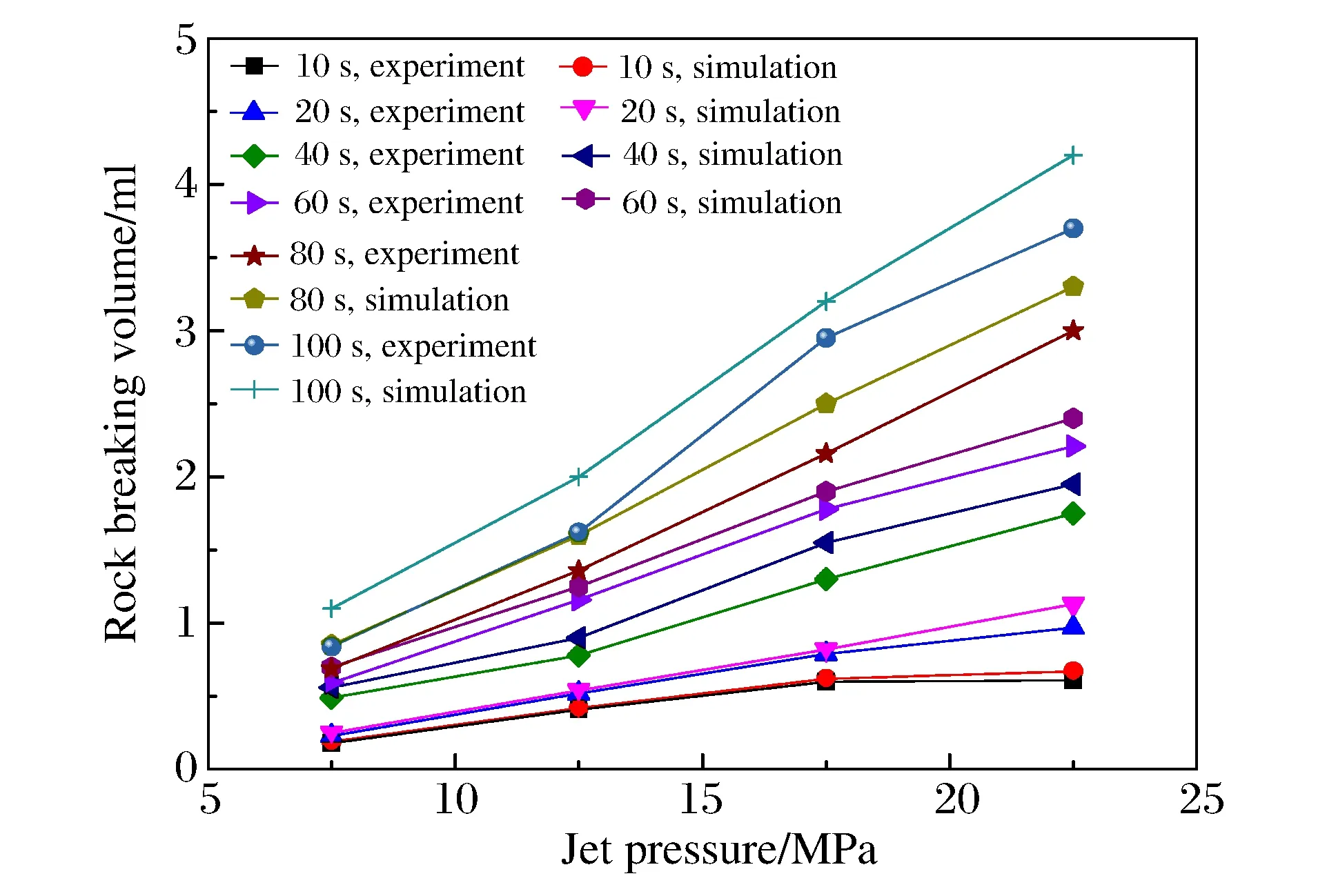
图9 粒子射流破岩体积随压力的变化Fig.9 Rock breaking volume caused by particle jet as a function of pressure

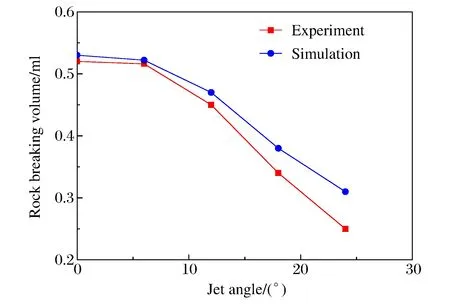
图10 粒子射流破岩体积随喷射角度的变化Fig.10 Rock breaking volume caused by particle jet as a function of jet angle

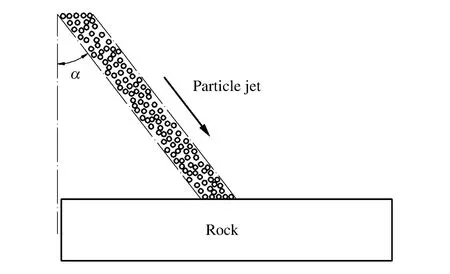
图11 粒子射流喷射角Fig.11 Particle jet angle

3.4 压力对粒子射流破岩效果的影响

由图9可知：冲蚀时间相同的条件下，随着压力的增大粒子射流破岩体积不断增大。射流压力增大，粒子射流速度增大，粒子动能增加，粒子具有更大的能量冲击岩石，与岩石产生瞬时冲击接触应力更大，因此产生破岩的体积更大。射流压力大于10 MPa后，曲线斜率增大，说明压力大于10 MPa后，粒子射流破岩的效率增大。存在粒子射流的能量临界值，只有粒子射流能量(射流压力)达到一定值后，才能实现岩石的高效破碎。因此，现场施工时，条件允许的情况下可尽量增大泥浆泵泵压，增大井下钻头喷嘴的射流压力，提高粒子射流的破岩效率。

3.5 喷射角度对粒子射流破岩效果的影响

由图10可知：数值模拟和室内实验结果表明，粒子射流冲蚀时间为20 s、压力为10 MPa时，粒子射流喷射角α增大(喷射角α为粒子射流和岩石法向方向的夹角，如图11所示)，粒子射流破岩体积先基本不变，喷射角大于6°后，破岩体积迅速减小。喷射角为0°～6°时，粒子在岩石表面法向方向的速度分量减小，切向方向的速度分量增大，削弱了粒子冲击破岩的效果，但影响较小；而且由于存在切向速度，粒子冲蚀岩石后，粒子以一定的角度反弹及时离开冲击坑，避免粒子聚集冲击坑后对后续粒子破岩造成影响，因此喷射角为0°～6°时，粒子射流的破岩体积基本不变。当喷射角大于6°时，粒子在岩石法向方向的速度分量不断减小，能够破碎岩石的能量降低，粒子能量利用率迅速降低，粒子法向速度分量减小对粒子破岩的影响起主导作用，因此粒子射流破岩体积不断减小。因此，在实际施工中，建议粒子射流喷射角控制为0°～6°。

4 结 论

(1)采用SPH方法开展射流条件下粒子冲击破岩的数值模拟，更符合现场实际条件，喷嘴中心轴线上粒子射流能量最大，喷嘴中心轴线方向上破岩的深度最大，粒子反弹和水射流对冲击坑共同修整作用，在岩石表面形成了较规则的V型冲击坑。

(2)射流压力相同的条件下，粒子射流破岩体积约为水射流破岩体积的2～4倍，粒子射流的破岩门限压力明显低于水射流破岩的门限压力，表明粒子冲击可以显著提高破岩效率。

(3)射流压力相同的条件下，随着粒子射流冲蚀时间的增加，破岩体积增加，单位时间内粒子射流破岩体积减小，即破岩效率降低，现场施工时需避免粒子射流对同一位置的持续冲蚀。相同冲蚀时间内，压力增大，破岩体积增加。射流压力大于10 MPa后，粒子射流破岩效率显著增大。现场施工时，可尽量增大泥浆泵泵压，增大井下钻头喷嘴的射流压力。粒子射流压力为10 MPa时，粒子射流喷射角增大，粒子射流破岩效率先基本不变后迅速减小，现场施工时建议粒子射流喷射角控制为0°～6°。

[1] Tibbitts G A, Galloway G G. Particle drilling alters standard rock-cutting approach[J]. World Oil, 2008,229(6):37-44.

[2] Tibbitts G A. Impact excavation system and method with suspension flow control: 7798249[P]. 2010-09-21.

[3] Galloway G G. Shot blocking using drilling mud: 8342256B2[P]. 2013-01-01.

[4] 赵健,韩烈祥,徐依吉,等.粒子冲击钻井技术理论与现场试验[J].天然气工业,2014,34(8):102-106. Zhao Jian, Han Liexiang, Xu Yiji, et al. A theoretical study and field test of the particle impact drilling technology[J]. Natural Gas Industry, 2014,34(8):102-106.

[5] 徐依吉,赵红香,孙伟良,等.钢粒冲击岩石破岩效果数值分析[J].中国石油大学学报(自然科学版),2009,33(5):68-69. Xu Yiji, Zhao Hongxiang, Sun Weiliang, et al. Numerical analysis on rock breaking effect of steel particles impact rock[J]. Journal of China University of Petroleum (Edition of Natural Science), 2009,33(5):68-69.

[6] 王政,倪玉山,曹菊珍,等.冲击载荷下混凝土动态力学性能研究进展[J].爆炸与冲击,2005,25(6):519-527. Wang Zheng, Ni Yushan, Cao Junzhen, et al. Recent advances of dynamics mechanical behavior of concrete under impact loading[J]. Explosion and Shock Waves, 2005,25(6):519-527.

[7] Wiederhorn S M, Lawn B R. Strength degradation of glass resulting from impact with spheres[J]. Journal of the American Ceramic Society, 1977,60(9):451-458.

[8] Sheldon G L. Effects of surface hardness and other material properties on erosive wear of metals by solid particles[J]. Journal of Engineering Materials and Technology, 1977,99(2):133-137.

[9] Evans A G, Gulden M E, Rosenblatt M. Impact damage in brittle materials in the elastic-plastic response regime[J]. Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 1978,361:343-365.

[10] Adler T A, Doan Ö N. Damage by indentation and single impact of hard particles on a high chromium white cast iron[J]. Wear, 1997,203/204(96):257-266..

[11] Wang J, Guo D M. A predictive depth of penetration model for abrasive water jet cutting of polymer matrix composites[J]. Journal of Materials Processing Technology, 2002,121(2):390-394.

[12] 王明波,王瑞和,陈炜卿.单个磨料颗粒冲击岩石过程的数值模拟研究[J].石油钻探技术,2009,37(5):34-38. Wang Mingbo, Wang Ruihe, Chen Weiqing. Numerical simulation study of rock breaking mechanism and process under abrasive water jet[J]. Petroleum Drilling Techniques, 2009,37(5):34-38.

[13] 况雨春,朱志谱,蒋海军,等.单粒子冲击破岩实验与数值模拟[J].石油学报,2012,33(6):1059-1063. Kuang Yuchun, Zhu Zhipu, Jiang Haijun, et al. The experimental study and numerical simulation of single particle impacting rock[J]. Acta Petrolei Sinica, 2012，33(6):1059-1063.

[14] 姜美旭.粒子冲击破岩规律的仿真研究及参数优化[D].北京:北京化工大学,2011:37-47.

[15] 伍开松,古剑飞,况雨春,等.粒子冲击钻井技术述评[J].西南石油大学学报(自然科学版),2008,30(2):142-146. Wu Kaisong, Gu Jianfei, Kuang Yuchun, et al. Comment on particle impact drilling technology[J]. Journal of Southwest Petroleum University (Science and Technology Edition), 2008,30(2):142-146.

[16] 孙占华.基于FE-SPH自适应耦合方法的弹靶侵彻动态响应分析[D].长沙：湖南大学,2012:8-27.

[17] 林晓东,卢义玉,汤积仁,等.基于SPH-FEM 耦合算法的磨料水射流破岩数值模拟[J].振动与冲击,2014,33(18):170-176. Lin Xiaodong, Lu Yiyu, Tang Jiren, et al. Numerical simulation of abrasive water jet breaking rock with SPH-FEM coupling algorithm[J]. Journal of Vibration and Shock, 2014,33(18):170-176.

[18] 张若棋,丁育青,汤文辉,等.混凝土HJC、RHT本构模型的失效强度参数[J].高压物理学报,2011,25(1):15-21. Zhang Ruoqi, Ding Yuqing, Tang Wenhui, et al. The failure strength parameter of HJC and RHT concrete constitutive models[J]. Chinese Journal of High Pressure Physics, 2011,25(1):15-21.

[19] 巫绪涛,李耀,李和平,等.混凝土HJC本构模型参数的研究[J].应用力学学报,2010,27(2):340-345. Wu Xutao, Li Yao, Li Heping, et al. Research on the material constants of HJC dynamic constitutive model for concrete[J]. Chinese Journal of Applied Mechanics, 2011,25(1):340-345.

[20] 段鹏.影响粒子冲击破岩效果主要因素的实验研究[D].青岛:中国石油大学(华东),2012:38-49.

(责任编辑 张凌云)

SPH-based numerical simulation and experimental study on rock breaking by particle impact

Zhao Jian1,2, Zhang Guicai1,2, Xu Yiji1, Zhou Yi1,Wang Ruiying1, Xing Xueyang1, Li Jianbo3

(1.CollegeofPetroleumEngineering,ChinaUniversityofPetroleum,Qingdao266580,Shandong,China；2.AcademyofScienceandTechnology,ChinaUniversityofPetroleum,Dongying257061,Shandong,China；3.CNOOCEnerTech-SafetyandEnvironmentalProtectionCo.,Tianjin300450,China)

Added into the drilling fluid in a volume portion of 1% to 3%, particles are capable of striking the rock with a high velocity after erupting from the bit nozzle and breaking the rock by particle impact combined with the mechanical action of the bit nozzle, thus greatly increasing the rock breaking efficiency. Using the transient nonlinear dynamics finite element simulation software and considering the influence of water jet, we established the physical model of rock breaking by particle impact based on the smoothed particle hydrodynamics (SPH) method, investigated the influence of the particle jet’s parameters on the rock breaking volume, and verified the simulation results by comparing them with those of the indoors experiment which could verify the effectiveness of the SPH simulation method. Our results show that a regulation V-shaped crater is formed by the particle jet impact; the rock breaking volume resulting from this particle jet impact is 2 to 4 times that of the volume from the water jet under identical conditions. The rock breaking volume increases over time, but in the meantime the rock breaking efficiency decreases. When the pressure of the particle jet is above 10 MPa, there is a great increase of the rock breaking efficiency. When the jet angle is above 6°, there is a quick decrease of the rock breaking efficiency.

particle jet; rock breaking by impact; SPH method; indoor experiment

10.11883/1001-1455(2017)03-0479-08

2015-09-07；

2015-11-25

中石油科学研究与技术开发项目(2015F-1801)；第58批中国博士后基金项目(2015M582167)； 中央高校基本科研业务费专项项目(16CS02061A)； 山东省自然科学基金项目(ZR2016EL10)；青岛市应用基础研究项目(16-5-1-37-jch)

赵 健(1987— )，男，博士，zhaojian-666@163.com。

O389 国标学科代码： 13035

A