电子测压器与铜柱测压器在膛压测试中结果差异分析*

尤文斌，马铁华，丁永红，张晋业

(1.中北大学电子测试技术重点实验室,山西 太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051;3.晋西集团技术中心,山西 太原 030027)

电子测压器与铜柱测压器在膛压测试中结果差异分析*

尤文斌1,2，马铁华1,2，丁永红1,2，张晋业3

(1.中北大学电子测试技术重点实验室,山西 太原 030051;2.中北大学仪器科学与动态测试教育部重点实验室,山西 太原 030051;3.晋西集团技术中心,山西 太原 030027)

火炮膛压作为火炮和弹药的内弹道重要参数，在研制、生产、交付、存储校验等环节都需要测量。针对当前同时采用放入式铜柱测压器和电子测压器测量某一批弹药时，电子测压器峰值出现散布较大，而铜柱测压法一致性好的问题，在分析两种测压法测压原理的基础上，利用铜柱动态校准数据作用到其ANSYS模型上修正了铜柱的Johnson-Cook模型参数；分析发现出现差异时电子测压器测量的压力变化率时程曲线不同，铜柱实际测试形变量与施加压力时程曲线作用于模型得到的形变量一致。研究表明：同时测量某一批弹药时，电子测压器比铜柱测压器出现压力峰值散布大的原因是由膛压上升过程变化率不同导致铜柱的应变率不同造成的。

火炮膛压；电子测压器；铜柱测压器；Johnson-Cook模型参数

火炮膛压是指火炮药室内火药高速燃烧使气体膨胀所产生的压力，用以推动弹丸实现发射[1]，一般火炮膛压小于700 MPa[2-3]。各种火炮系统在出厂前都必须进行膛压测试，以便于考核火炮的精度、强度等指标是否满足设计要求[4-6]。2008年，铜柱、铜球测压，引线式测压及放入式电测压3种方法被作为膛压测试的并行标准写入由中国人民解放军总装备部制定的《火炮内弹道试验方法》中[5]。

放入式电子测压器与铜柱测压器同时测量一批弹药的发射膛压，在90%的测试中两者测量结果相对误差小于0.5%[7]；但是，在某些批产品测量结果中出现了电子测压器测得峰值压力散布大,而铜柱测得的峰值压力一致性好的现象。本文中主要通过对内置式电子测压与铜柱测压产生差异的机理和实验数据的分析，探究在测量同一批弹药时，放入式电子测压器与铜柱测压器出现差异的机理，以期为后续工作提供依据。

1 膛压测试原理

根据敏感元件的不同，膛压测试方法主要有两种：塑性变形测压法和弹性变形电测法[8]。

1.1 放入式铜柱测压器原理—塑性变形测压法

放入式铜柱测压器的工作原理如图1所示。将测压器置入火炮膛底,发射药燃烧压力p(t)经硅脂传递到活塞后，再作用到铜柱上,使其产生轴向压缩变形，p(t)卸载后，铜柱具有残余变形量，则可通过残余变形量得到峰值压力pm。铜柱测压整个过程中应力应变如图2所示，压力小于比例极限σp为直线段OA，弹性极限σe前的AB段是弯曲的，在这个阶段卸除载荷，应力和应变都随原有曲线降到零。超过σe以后，铜柱开始屈服并进入塑性变形阶段，对应的应力称为屈服应力σs，当压力达到最大时，应力达到最大为σm，压力卸载后，应力应变将不再沿着原有曲线退回原点O，应力沿一条近似平行于OA的MF线下降为零，而应变则停留在F点，其值为εr。通过以上分析可知，pm越大，σm就越大，εr也越大，因此通过测量εr的大小就可判定压力峰值pm[9-10]。

图1 铜柱测压器工作原理Fig.1 Copper cylinder pressure gauge’s working principle

铜柱产生动态误差的主要原因缘于塑性敏感元件的应变率效应，即塑性变形的抗力不仅和变形量有关，还和变形速率有关，应变率越大，屈服极限应力越高，因此在相同压力的情况下，静态加载时应变最大，动态载荷下变形量减小，从而产生负误差[7,9-10]。

图2 铜柱受压应力应变曲线Fig.2 Copper cylinder’s stress-strain curve

1.2 放入式电子测压器原理—弹性变形电测法

放入式电子测压器由压电式压力传感器、电荷放大器、A/D转换器和存储模块构成，如图3所示[7]。传感器将膛内压力的变化转换为电荷量的变化，经电荷放大器转换成电压信号，再经A/D转换器变换为数字量编码存储。

压电式压力传感器的压电元件夹于2个弹性膜片之间，膜片采用弹性材料，当外力作用在膜片上时，膜片将作用在表面的压力传递给石英晶体，由弹性理论的胡克定律得F=kx=pS，其中F为作用力，k为物体的劲度系数，x为弹性形变量，p是压强，S为传感器膜片面积。石英晶体受到外力F作用时，内部会产生电极化现象，且会在某两个表面上产生符号相反的电荷；在外力F撤消后，晶体又会恢复到不带电的状态。晶体受力后，所产生的电荷量Q与外力F成正比[11]，Q=dF，d为压电系数，也可以表示为Q=dpS。

图3 电子测压器的系统原理图Fig.3 Schematic diagram of internal pressure gauge

由于膜片面积S是确定的，因此膜片将作用于传感器受力面的压强转化为与压力成正比的力传递给石英晶体，即产生与压强成线性正比的电荷。为了提高测量精度，本放入式电子测压器的传感器选用瑞士Kistler公司的6215型石英压力传感器 (1994年成为北约组织内弹道膛压测量标准) ，其固有频率大于240 kHz[7]。膛内压力的频率在5 kHz以内，电荷放大器在这个频带区间可以达到2‰的误差；12位AD变换器带来的量化误差小于1‰；数字信号在存储电路中不会产生误差。因此，出现误差的环节主要在于压力传感器。

2 放入式铜柱测压的ANSYS模拟

铜柱测压中所使用的铜柱是高导无氧铜，其材料特性为刚塑性硬化材料，在受压变形过程中会产生较大的塑性变形，因此采用弹塑性有限元法分析。

2.1 铜柱的材料模型

通常采用Johnson-Cook模型对火炮膛压作用下的铜柱材料进行描述，由于Johnson-Cook模型属于应变率相关本构模型，因此主要考虑流动应力的应变率效应，屈服应力σy可表示为[7,12]：

(1)

2.2 放入式铜柱测压的ANSYS模型

由于铜柱测压器具有轴对称性结构，为了缩短仿真的计算时间，利用ANSYS建立的1/4对称物理模型如图4所示，由壳底、铜柱和活塞3个部分组成。其中，壳底和活塞材料为钢，采用弹性体模型，其具体参数：密度为7.83×10-3g/mm3，弹性模量为200 GPa，泊松比为0.32。铜柱材料为高导无氧铜，采用弹塑性模型，其Johnson-Cook模型静态参数的初始值可查阅文献[13]。Grüneisen状态方程中常数a=0.47，γ0=2.02，S1=1.489，S2=S3=0，C=3 940 m/s，质量热容为0.39 J/(g·K)。将壳底固定后，在活塞上表面施加压力，铜柱受压力变形后获取对称圆柱变形如图5所示。

图4 ANSYS结构模型Fig.4 ANSYS structural model

图5 受压变形效果图Fig.5 Compression deformation

2.3 铜柱的Johnson-Cook模型参数的修正

由于膛压是动态压力，铜柱的动力特性与静力特性区别很大，铜柱的主要动力特性—瞬时应力随应变率的增大而增大[14]。直接使用ANSYS/LSDYNA系统自带的静态Johnson-Cook模型参数，计算结果会和实测结果存在较大误差。为解决这个问题，对铜柱测压器施加脉宽6 ms的半脉冲压力，进行落锤实验[7,9]，将得到的压缩量作为动态Johnson-Cook模型的实验数据，对模型参数进行修正，修正后剪切模量为47 GPa，屈服应力常数A=91 MPa，应变硬化指数n=0.233。在ANSYS/LSDYNA中利用修正后的模型参数对铜柱进行数值模拟[7]，计算结果与实验数据对比及相对误差如表1所示。

表1 实验数据与数值模拟结果对比

表中，pm为落锤施加半正弦压力脉冲峰值，τ为脉冲宽度。由表1可知最大误差为0.359%，验证了修正后的Johnson-Cook模型参数正确性。

3 放入式电子测压器与铜柱测压器测试结果差异性分析

放入式电子测压器与铜柱测压器使用前都经过了动态校准，在某加农炮同批次装药的膛压测试中，两者测得其中的两发弹药的压力峰值如表2所示，铜柱测得的压力峰值接近，相差0.7 MPa，电子测压器测得压力峰值相差较大，相差2.5 MPa。

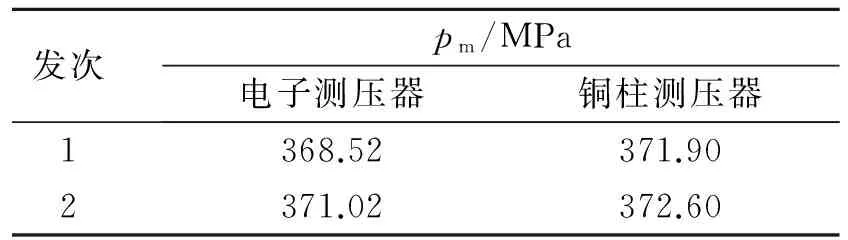
表2 不同传感器实测压力峰值对比

铜柱形变量在瞬态压力作用下，受应变率影响较大，压力变化速率与应变率有关，直接测量铜柱压缩量获得峰值压力的方法不能分析出现差异的原因。为此，通过将电子测压器记录的压力时程曲线对时间求导，比较压力时程曲线与压力变化率时程曲线的差异[7]。电子测压器记录的压力时程曲线和压力变化率时程曲线如图6所示。将压力曲线上升到峰值前的压力变化率部分进行局部放大得到图7。

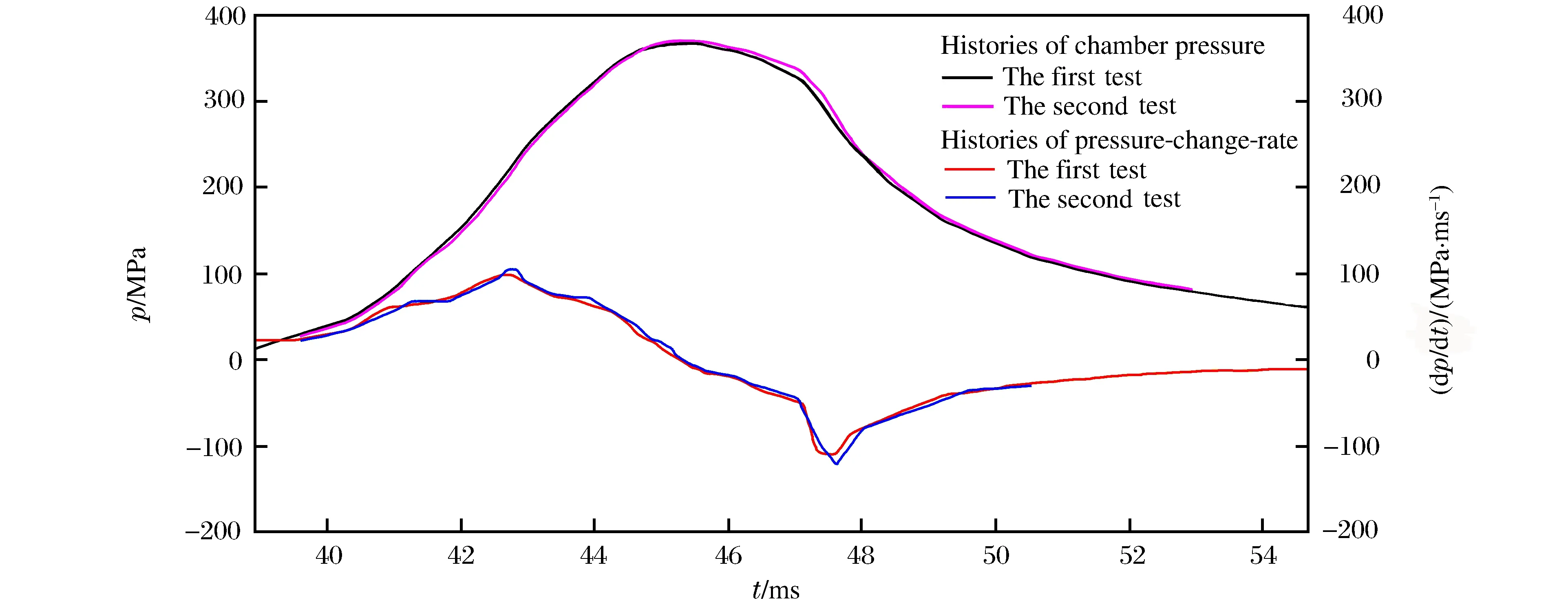
图6 压力和压力变化率时程曲线Fig.6 Histories of pressure and pressure change rate

图7 压力变化率时程曲线局部放大Fig.7 Local amplification of pressure-change-rate histories

从图7中可以看出，在压力达到峰值前这一段时间第2发实验的压力变化率稍大于第1发的，又由于第2发实验的压力峰值大于第1发的，峰值最终起到了主导作用。在两者综合作用下，造成电子测压器与铜柱测得的压力相差较大，同时也表现出电子测压器测得压力峰值散布大于铜柱测得的。

为了找出电子测压器与铜柱测压器测得压力之间的关系，将2发实验电子测压器测得的压力时程曲线作为铜柱测压器的输入压力代入ANSYS/LSDYNA铜柱测压模型中，得到图8中所示铜柱压缩的形变量时程曲线，从图8中可知，计算得到的第1发实验的形变量为-1.629 7 mm，第2发实验的形变量为-1.637 4 mm。而实测第1发实验铜柱的形变量为-1.629 0 mm，第2发实验铜柱的形变量为-1.635 0 mm，数值模拟结果与实测数据一致。

图8 2次实验中铜柱形变量的计算结果Fig.8 Simulation results of copper cylinder deformation

4 结 论

通过分析铜柱测压器和电子测压器的测压原理，确定两者测量误差可能出现在铜柱本构特征的应变率效应上，建立了铜柱测压器的ANSYS模型，并由铜柱动态校准数据修正了铜柱的Johnson-Cook模型参数并进行验证。电子测压器测得的压力曲线作用到铜柱模型获得的变形量与铜柱实测变形量一致，该批弹药膛压上升速率不一致，导致铜柱测压器在应变率效应作用下产生了误差，表现出铜柱所测压力峰值趋于一致的假象。

[1] 金志明,翁春生,宋明.高等内弹道学[M].北京:高等教育出版社,2003:1.

[2] 李新娥,祖静,徐鹏.新型应变式高膛压测试系统研制[J].高压物理学报,2011,25(4):310-316. Li Xin’e, Zu Jing, Xu Peng. A novel strain type high chamber pressure test system[J]. Chinese Journal of High Pressure Physics, 2011,25(4):310-316.

[3] 刘林林,马忠亮,萧忠良.变燃速发射药膛内燃烧与内弹道过程研究[J].兵工学报,2010,31(4):409-413. Liu Linlin, Ma Zhongliang, Xiao Zhongliang. Research on the actual combustion and interior ballistics process of the variable-burning rate propellant in cannon[J]. Acta Armamentarii, 2010,31(4):409-413.

[4] Walton W S. Electrical measurement of weapon chamber pressure: ADP002684[S]. Aberdeen Proving Ground MD Materiel Testing Directorate, 1995.

[5] 中国人民解放军总装备部测量通信总体研究所.火炮内弹道试验方法:GJB 2973A-2008[S].北京:总装备部军标出版发行部,2008.

[6] Li Xin’e, Zu Jing, Ma Tiehua, et al. Research on a novel capacitive pressure sensor to measure chamber pressures of different caliber artilleries[J]. IEEE Sensors Journal, 2011,11(4):862-868.

[7] 尤文斌,马铁华,丁永红,等.铜柱测压器膛压测试产生误差的机理研究[J].仪器仪表技术,2015,36(10):2290-2296. You Wenbin, Ma Tiehua, Ding Yonghong, et al. Deviation mechanism research for copper cylinder pressure gage in the artillery chamber pressure test[J]. Chinese Journal of Scientific Instrument, 2015,36(10):2290-2296.

[8] Carson J A, Dimeff J, Charters A C. Piston type strain gauge for measuring pressures in interior ballistics research[J]. Review of Scientific Instruments, 1955,26(9):879-883.

[9] 孔德仁.塑性测压器材准动态校准技术及实验研究[D].南京:南京理工大学,2003.

[10] 张淑宁.准动态校准技术实验研究[D].南京:南京理工大学,2003.

[11] 边义祥,杨成.基于压电材料的振动能量回收技术现状综述[J].压电与声光,2011,33(4):612-622. Bian Yixiang, Yang Chenghua. A review of current research for energy harvesting based on vibration of piezoelectric materials[J]. Piezoelectrics and Acoustooptics, 2011,33(4):612-622.

[12] Johnson G R, Inc H, William H C. A constitutive model and data for metals subjected to large st rains, high tempreture[C]∥Proceedings of 7th International Symposium on Ball. The Hague, Netherlands: International Ballistics Committee, 1983:541-547.

[13] 吕剑,何颖波,田常津,等.泰勒杆实验对材料动态本构参数的确认和优化确定[J].爆炸与冲击,2006,26(4):339-344. Lü Jian, He Yingbo, Tian Changjin, et al. Validation and optimization of dynamic constitutive model constants with Taylor test[J]. Explosion and Shock Waves, 2006,26(4):339-344.

[14] 孔德仁,朱明武.铜柱、铜球准动态校准的机理[J].南京理工大学学报(自然科学版),2004,28(4):375-379. Kong Deren, Zhu Mingwu. Mechanism of quasi-dynamic calibration for copper cylinder and copper ball[J]. Journal of Nanjing University of Science and Technology (Natural Science Edition), 2004,28(4):375-379.

(责任编辑 王易难)

Deviation research on internal electronic pressure gauge and copper cylinder pressure gauge in artillery chamber pressure test

You Wenbin1,2, Ma Tiehua1,2, Ding Yonghong1,2, Zhang Jinye3

(1.Science and Technology on Electronic Test and Measurement Laboratory,North University of China, Taiyuan 030051, Shanxi, China;2.Key Laboratory of Instrumentation Science and Dynamic Measurement Ministry of Education,North University of China, Taiyuan 030051, Shanxi, China;3.Jinxi Industries Group Technology Center, Taiyuan 030027, Shanxi, China)

The artillery chamber pressure is so important a parameter for interior ballistic performance that it has to be measured repeatedly in the course of artillery development, production, acceptance, storage check. When a batch of ammunitions are measured by internal electronic pressure gauge (IEPG) and copper cylinder pressure gauge (CCPG) at the same time, the distribution of IEPG peak values is found to be much larger than that of CCPG ones. The ANSYS model of CCPG was proposed based on the CCPG working principle, and the Johnson-Cook model parameters were optimized according to the dynamic calibration data. The results shows that when discrepancy occurred with respect to the peak pressures measured respectively by IEPG and CCPG, the pressure-change-rate histories of IEPG were different, and the test pressure exerted on the CCPG model was consistent with the copper cylinder deformation obtained in the copper test. The results also show that the difference in peak pressure, captured by IEPG and CCPG in a batch of ammunition chamber pressure measurement at the same time, is due to the influence of different copper cylinder strain rates as a result of different rising rates of the chamber pressure.

artillery chamber pressure; internal electronic pressure gauge; copper cylinder pressure gauge; Johnson-Cook model parameter

10.11883/1001-1455(2017)03-0571-06

2015-07-22；

2015-12-28

国家自然科学基金项目(61471385);中北大学电子测试技术重点实验室基金项目(9140C120409)

尤文斌(1981— )，男，博士，副教授，硕士生导师，youwenbin@nuc.edu.cn。

O384 国标学科代码：1303520

A