基于多轴应力损伤的薄板花瓣型破口形成机理研究*

李 营,吴卫国,张 磊,杜志鹏,张 玮,赵鹏铎

(1.武汉理工大学交通学院,湖北 武汉 430063;2.海军装备研究院,北京 100161)

基于多轴应力损伤的薄板花瓣型破口形成机理研究*

李 营1,2,吴卫国1,张 磊2,杜志鹏2,张 玮2,赵鹏铎2

(1.武汉理工大学交通学院,湖北 武汉 430063;2.海军装备研究院,北京 100161)

开展了多种应力状态下的船用钢力学特性实验，基于多轴应力状态损伤的失效准则研究了局部冲击荷载作用下圆形板的花瓣型破口形成过程，划分了花瓣型破口形成的3个阶段，分析了裂纹区域、非裂纹区域应力状态变化过程及损伤情况。得到:(1)考虑多轴应力损伤的舰船用钢失效准则能有效预测受力状态复杂的花瓣状破口；(2)花瓣型破口的形成主要分为蝶形凹陷、中心区域裂纹扩展、花瓣形成与翻转等3个阶段；(3)花瓣型破口的裂纹区和非裂纹区均受力复杂，破口预测须考虑应力状态对损伤特性的影响；(4)花瓣形成过程中，第1阶段和第3阶段均匀变形，第2阶段损伤局部化明显，花瓣卷曲会造成花瓣根部的二次损伤。

花瓣型破口；应力三轴度；应力状态；失效准则

水面舰艇结构在战时易遭受鱼雷、水雷和反舰导弹的攻击，造成舰艇结构破损甚至断裂。由于爆炸实验耗费巨大的财力、物力，数值仿真成为有效的辅助手段。数值仿真效果取决于两个方面，即精确的算法和良好的材料性能表征。而数值模拟所产生的误差中，材料表征带来的误差远大于计算程序数值求解带来的误差[1]。准确的材料断裂表征参数是开展爆炸作用下舰船结构毁伤模式预测与评估的重要前提。花瓣型破口是爆炸作用下板架结构的重要破坏模式之一[2]。对花瓣性破口的数值模拟和理论分析一般基于单向应变假设和双向应变假设[3]，设定断裂应变为某一具体塑性应变值。但基于板架爆炸实验的终点效应，反推破口处等效塑性应变值的方法有一定的误差，且不同实验给出的结果差异较大，给参数的选择带来一定的困难：牟金磊等[3]开展水下爆炸实验，分析了破口裂纹处的厚度变化，提出采用0.388作为失效应变判据；陈长海等[4]则根据空中接触爆炸的实验结果提出断裂应变的极限值为0.605，在数值模拟中采用了塑性应变0.28作为断裂应变[5]。爆炸作用下金属材料的失效与应力状态密切相关[6]：在单向拉伸到双向拉伸过渡区域，金属材料断裂应变呈指数递减[7]；在多向受压应力状态下，金属材料甚至完全不会失效[8]。在爆炸荷载作用下，花瓣型破口是否为简单的单向拉伸或者双向拉伸，应力状态又如何影响损伤断裂过程，值得深入研究。本文中，分析不同应力状态下船用钢的断裂应变，基于多轴应力损伤的ABAQUS子材料断裂准则模型对局部冲击作用下花瓣型破口的形成过程进行计算，分析断裂区、非断裂区的应力状态变化，局部损伤特性等，论证花瓣型破坏模式下应力状态变化对准确预测破坏程度和破口大小的重要性。

1 船用钢断裂特性

1.1 材料实验

船用钢较一般结构钢强度高、韧性强，对爆炸冲击等载荷具有更强的抗力。单轴受拉应力状态下船用钢的失效特性由拉伸实验获得。试件参照《GB/T228-2002》[9]制作。试件为板状，厚2.7 mm，设计实验段长度为40 mm。在常温20 ℃的环境下，使用微机控制万能材料试验机(INTRON5882)以5 mm/min的拉伸速度进行准静态拉伸实验。通过迭代有限元参数输入的方法对比力-位移曲线，不断校正应力应变关系。拉伸试样力-位移曲线如图1所示。

如图2所示，设计纯剪切试样的单向拉伸实验实现剪切应力状态,试样厚度分别为2.7和4.7 mm。与缺口圆棒拉伸实验不同，剪切件在断裂时的等效塑性应变难以通过理论公式确定。以中间断面为研究对象进行了有限元迭代校正，直到数值模拟与实验的力-位移曲线十分接近为止，通过多次修正，有限元计算结果与实验结果较一致。

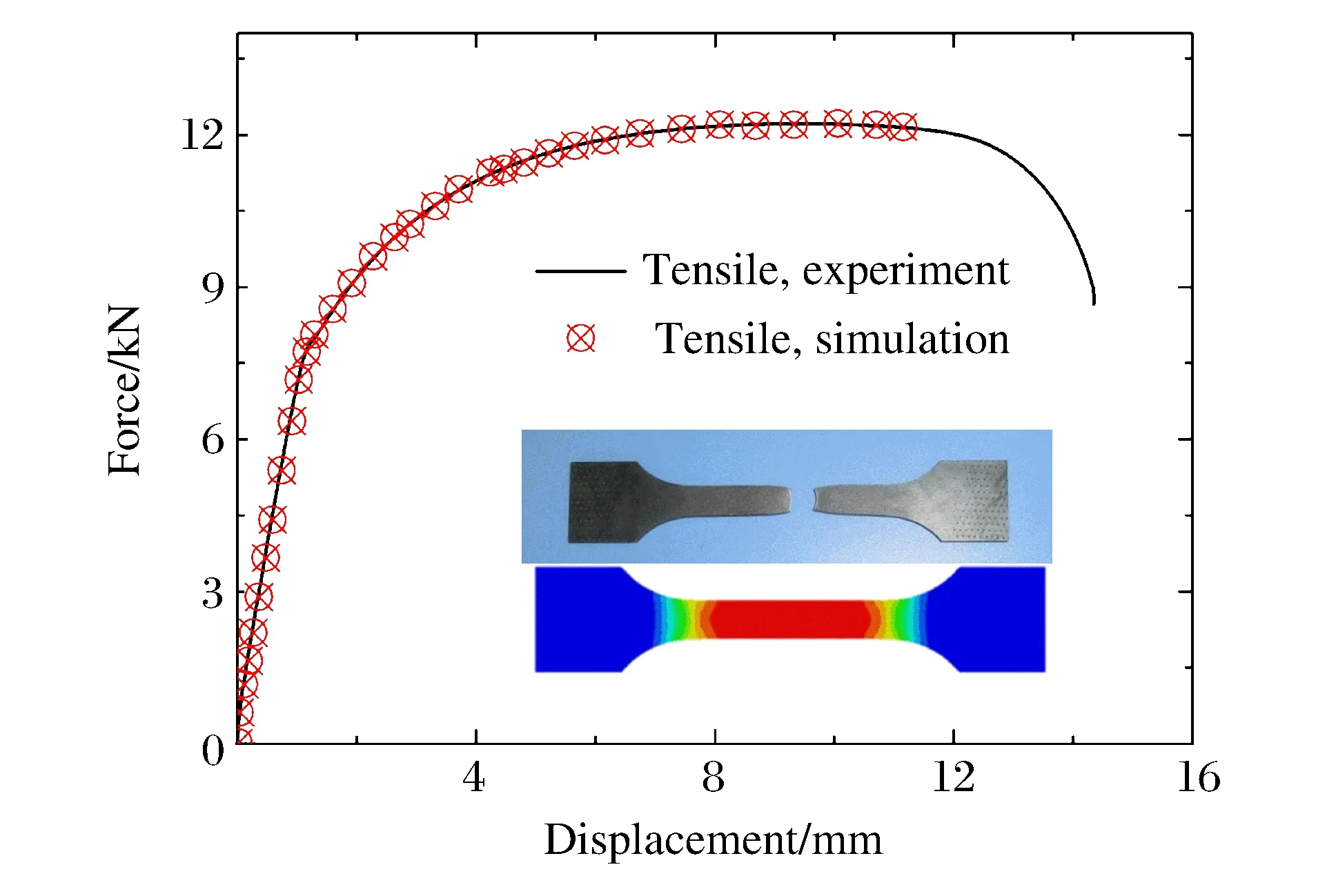
图1 拉伸试样及力-位移曲线Fig.1 Tensile specimen and its force-displacement curves

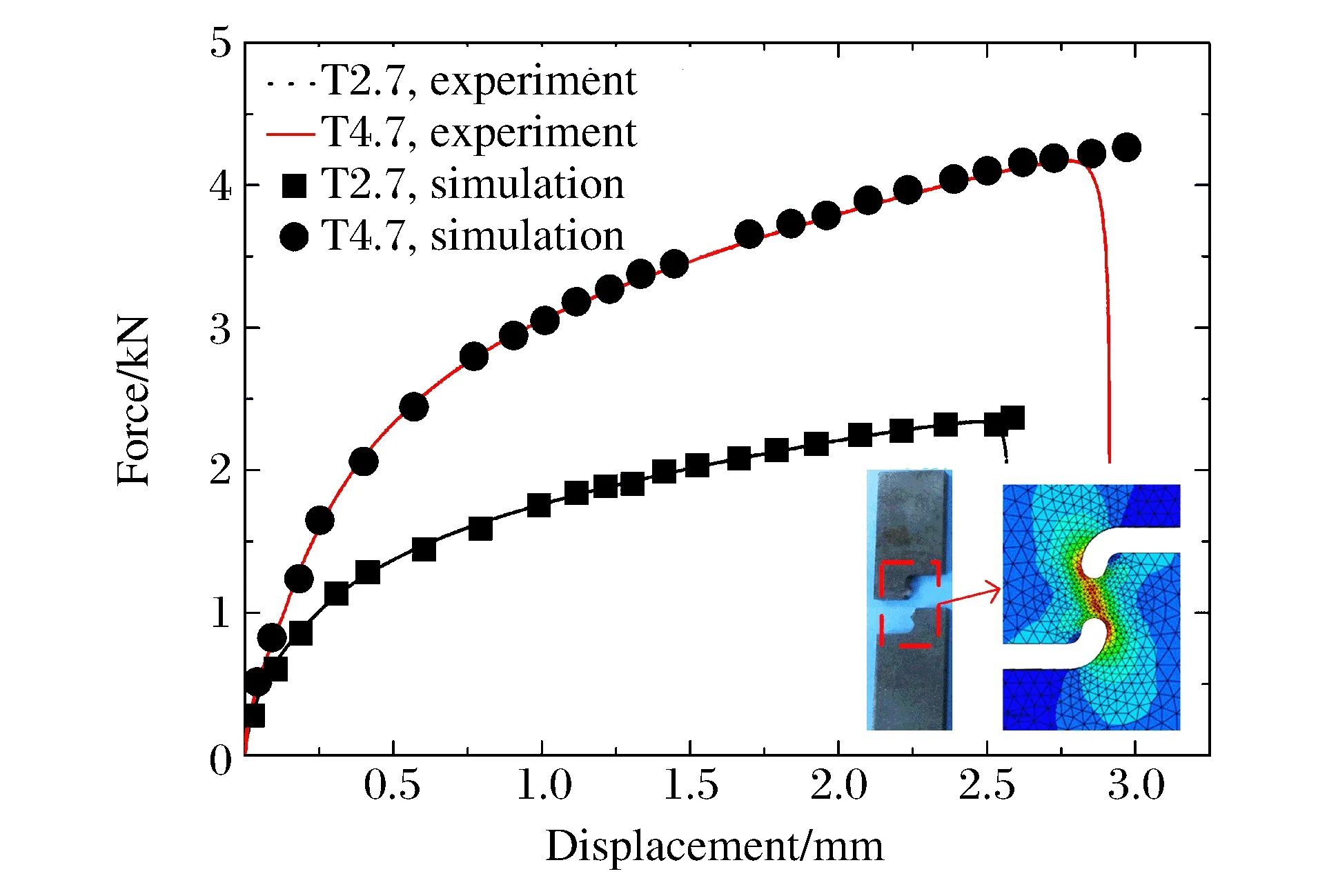
图2 剪切试样及力-位移曲线Fig.2 Shear specimen and its force-displacement curves

1.2 断裂准则

对不同应力状态下的船用钢实验结果采用下式[10]：

(1)

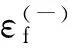
为计算变形过程中的损伤，定义单元的损伤为:

D=Δεp/εf

(2)

式中：D为损伤参数，D=0～1，初始时D=0，当D=1时材料失效； Δεp为一个时间步的塑性应变增量，εf为当前时间步断裂应变。

不同断裂准则对断裂应变值的预测结果如表2所示,εf,exp为断裂应变实验值。可以看出，采用新断裂准则的预测结果εf,new明显好于采用常用等效塑性应变准则的预测结果εf,nom。

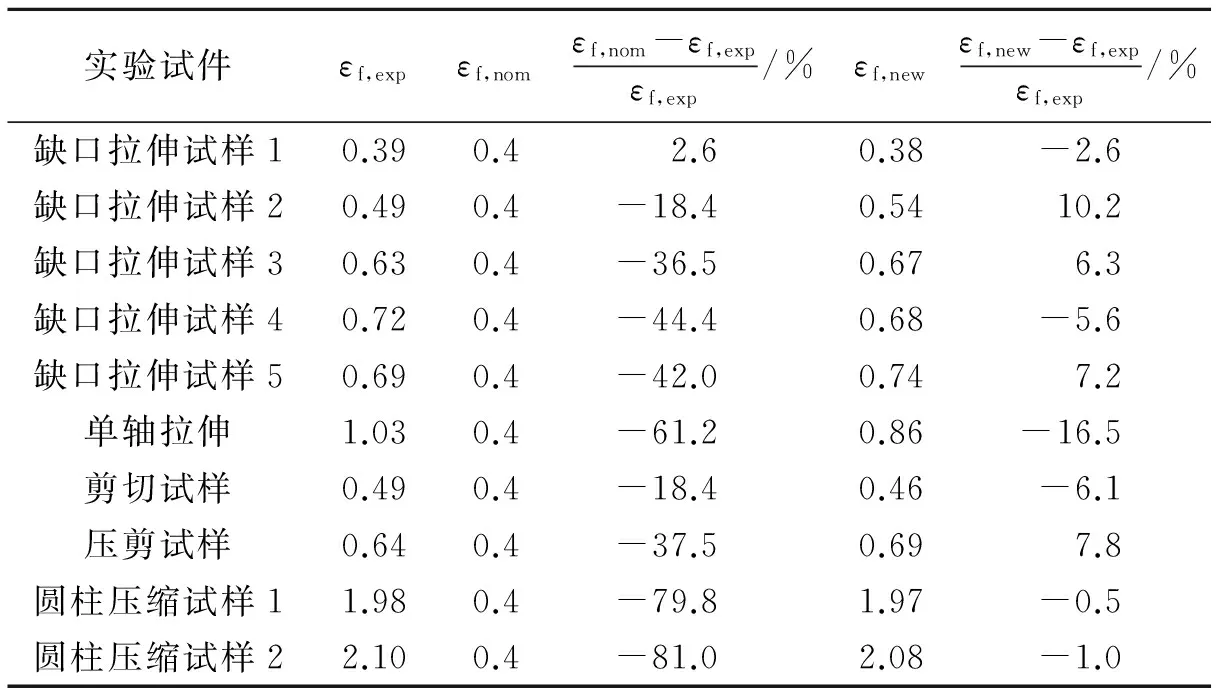
表1 不同准则预测的断裂应变值

2 局部冲击载荷下的花瓣型破口

2.1 花瓣状破口的形成过程

采用ABAQUS建模计算，建立直径为600 mm的圆形薄板，设置为板单元，厚度为3 mm，四周边界固定约束。中心直径为50 mm的核心区域通过施加初速度(100 m/s)的方式加载局部冲击载荷。

图3为花瓣型破口形成过程的俯视和侧视图。由图3可以看出，整个花瓣变形分为3个阶段：(1)蝶形凹陷阶段,如图3(a)～(b)所示,中间局部区域受冲击载荷作用出现局部凹陷，在中心运动区域与未运动区的过渡区域，由于速度梯度较大，易发生较大的塑性变形，整体呈现凸台状，出现局部颈缩，甚至整个中心运动区域飞出，形成充塞破口;(2)中心区域裂纹扩展阶段，如图3(c)～(d)所示，在蝶形凹陷区边界与中心处，由于变形梯度较大，形成若干裂纹，在局部结构继续运动的情况下，主裂纹长度持续增大，并发生扩展，中心区域出现局部碎裂破片；(3)花瓣形成与翻转阶段，如图3(e)～(f)所示，中心区域碎片继续飞出，裂纹此时不再扩展，花瓣因后续惯性与径向拉力联合作用向后翻转，发生较大塑性变形，花瓣最终形成。

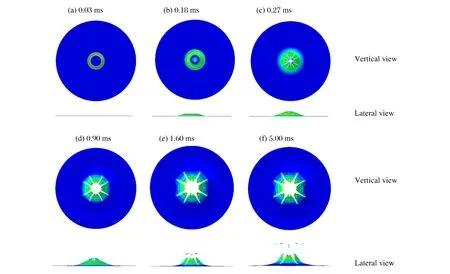
图3 花瓣型破口形成过程Fig.3 Petaling formation process

2.2 典型区域应力状态

图4为裂纹扩展区域不同位置失效单元的应力三轴度变化曲线。3个不同测点距离圆心80、52和33 mm，分别位于花瓣间裂纹区、蝶形凹陷过渡区及中心运动区域内。3个测点位置的单元均先受拉伸作用，接着过渡到拉剪、剪切和压缩区，并依次发生损伤。从应力三轴度的变化可以看出，整个花瓣变形过程中，各失效单元的受力状态发生较大变化，单一的双向受拉无法准确描述。

图5为非碎裂区不同位置处应力三轴度变化曲线。花瓣区、圆板边缘及中间过渡区受力状态有明显差异：(1)花瓣区(element at petal)最早受到拉伸作用，应力三轴度约为0.6，属于双向拉伸，接着花瓣裂纹扩展形成自由界面，拉伸波转换成压缩波，局部受力由双向拉伸转换成双向压缩，接着由于花瓣顶部位置翻卷，花瓣中的单元受到较持续的拉伸作用；(2)接近边缘处的测点(element at edge)则在作用开始时间上滞后于花瓣和过渡区，受到一段持续时间较长的拉伸作用，后续也会进入交替的拉伸和压缩作用，偶有剪切应力状态，但整体上看，后期(2.4 ms以后)主要受拉伸作用；(3)花瓣和边界的过度区内(element between edge and petal)，测点受拉伸作用的起始时间介于花瓣和边缘之间，起初受到较长时间双向拉伸波的作用，接着由于反射波的作用测点承受剪切甚至压缩作用的交替作用，稍后由于花瓣的向外翻转，测点将承受较长时间的拉伸作用。

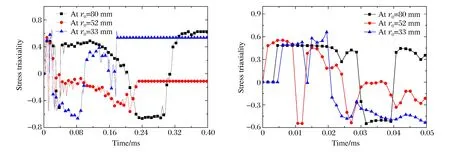
图4 裂纹扩展区失效单元的应力三轴度Fig.4 Stress triaxiality of failure elements at crack

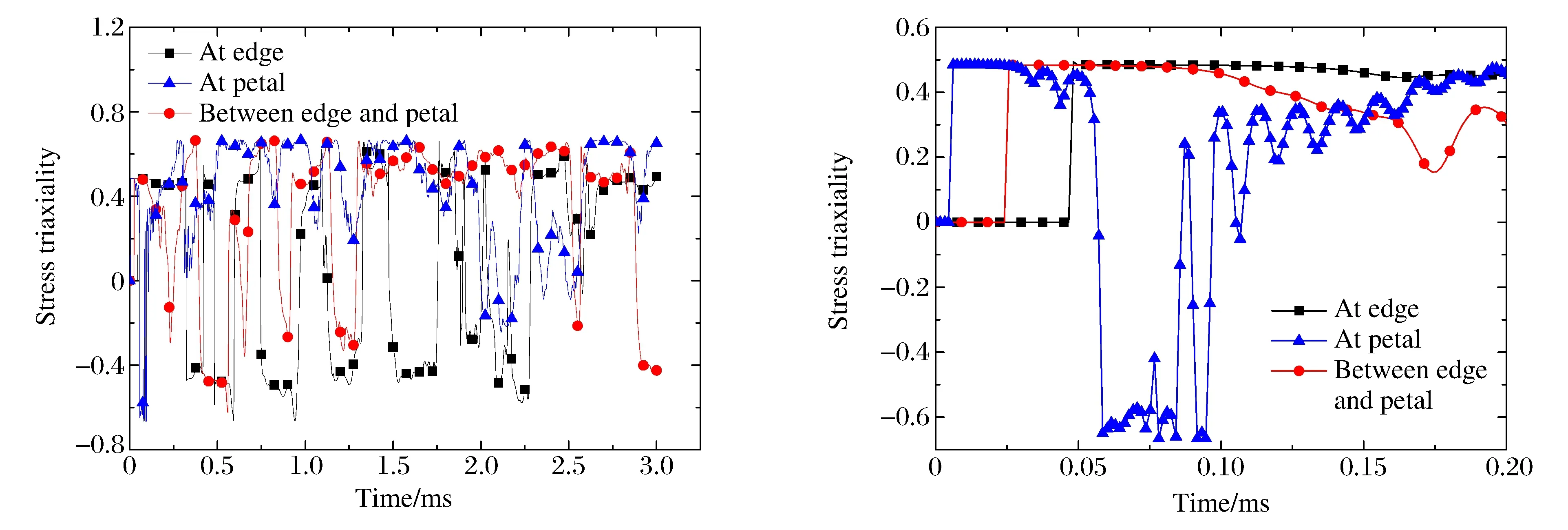
图5 非裂纹区单元的应力三轴度Fig.5 Stress triaxiality of elements out of crack

2.3 局部损伤程度

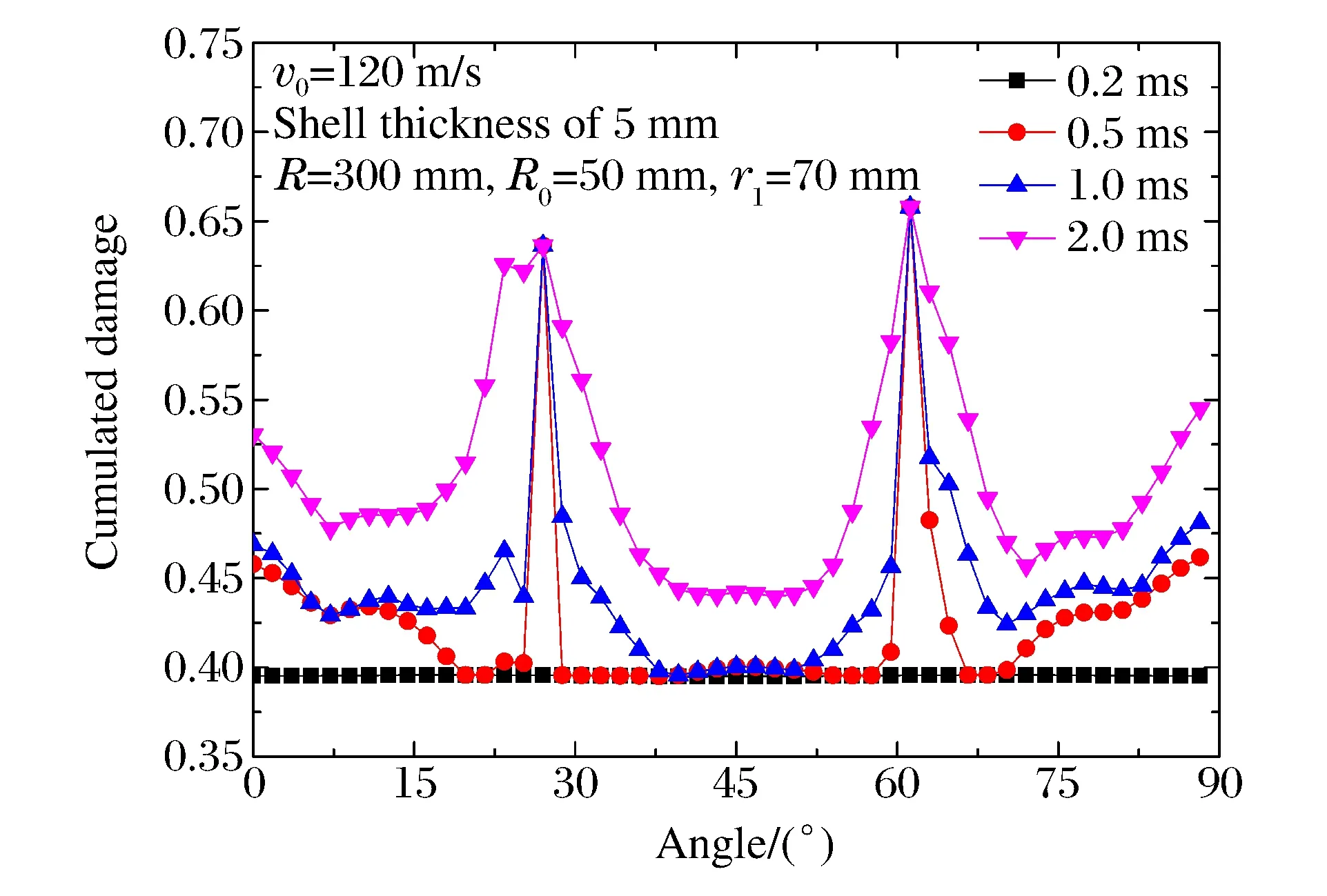
图6 裂纹区环向单元累积损伤Fig.6 Cumulated damage of elements at crack

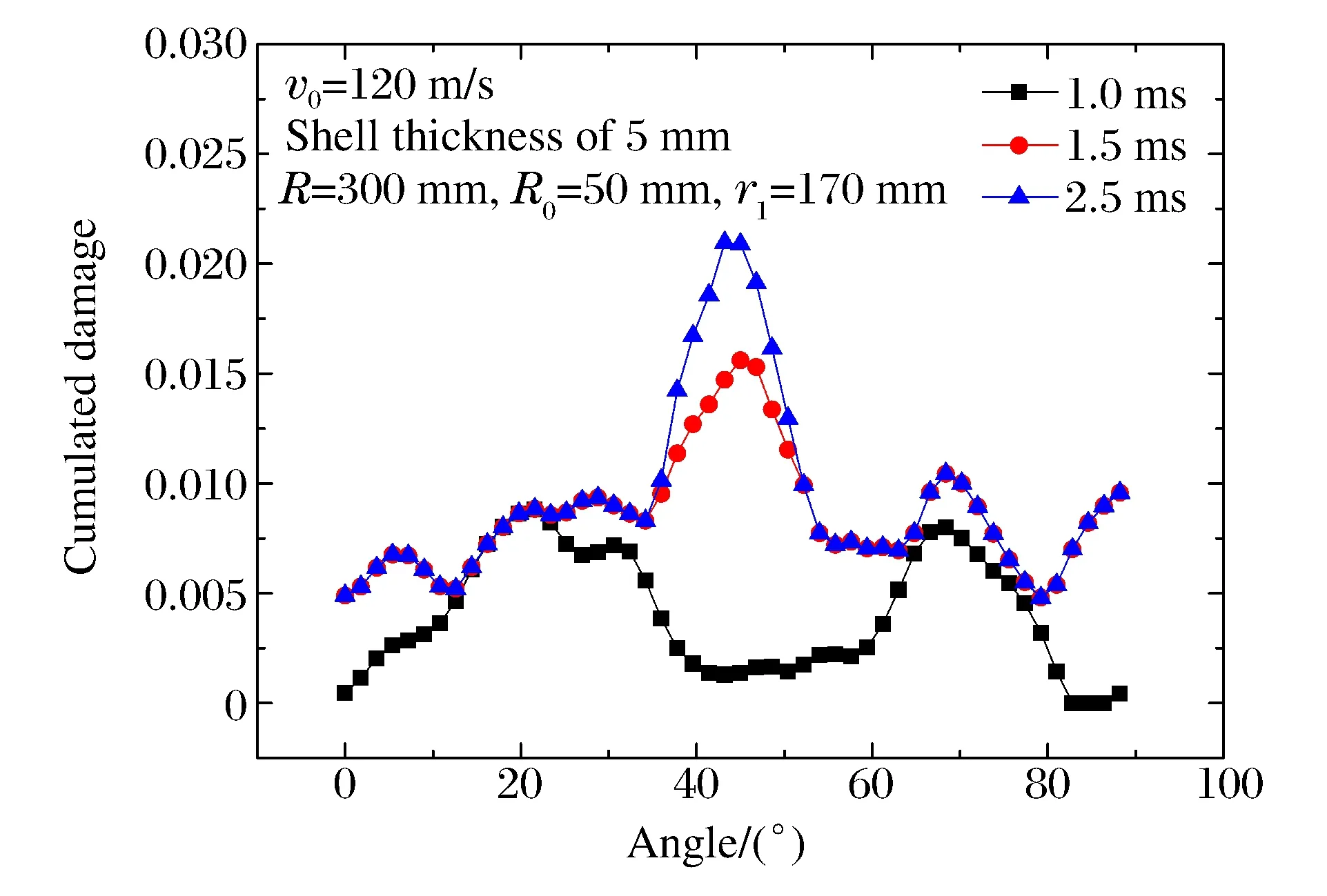
图7 非裂纹区环向单元累积损伤Fig.7 Cumulated damage of elements out of crack

图6为距中心70 mm处的累积损伤情况(0°～90°范围内),图中R为圆板直径，R0为加载区域半径。与2.1节对应，各曲线从时间和物理阶段的不同划分为3个阶段，分别为：(1)蝶形凹陷造成的均匀加载，各测点损伤较一致，均小于0.4(0.2 ms时的曲线)；(2)裂纹迅速扩展形成(0.5 ms)时，28°与62°处的损伤迅速发展，形成2个“山峰”，并远大于周围值；1.0 ms时，峰值附近的值有一定的塑性累积，损伤度稍有增大；(3)花瓣翻转造成的均匀损伤，该阶段特征为，除“山峰”外，其他各处的损伤程度均有一定程度的增大，且幅值基本相当(2.0 ms时的曲线)。

图7为距中心170 mm处的累积损伤情况(0°～90°)。不同区域的损伤发展先后不同，首先为28°与62°处裂纹前端产生明显损伤(1.0 ms)，其他区域发展不明显；1.0 ms后，裂纹前端区发展不明显，2个裂纹中间由于花瓣的弯曲，形成一定的塑性损伤区。说明花瓣卷曲会造成花瓣根部的二次损伤。

3 探 讨

由上述分析可以看出，爆炸等局部冲击作用下，薄花瓣型破口形成过程受力状态复杂，远非双向受拉所能描述。图8为薄板爆炸后形成的花瓣与碎裂与文献[4,12]实验结果比对的情况。可以看出，考虑应力状态的断裂准则对于准确预测花瓣的形成，以及爆炸碎片的预测和描述较适用。传统的等效塑性应变准则，将失效参数设置为一常数，不考虑应力状态的影响，难以描述复杂应力状态下板的破坏机理。考虑应力状态对金属材料影响的失效准则，才能揭示花瓣型破口形成机理，更有效地预测复杂应力状态下的薄板失效模式和破口大小。图9为采用等效塑性应变准则获得的破坏模式，可以看出与考虑应力状态的准则得到的破坏模式具有较大差异。表明考虑应力状态的材料失效准则对于准确预测花瓣型破口具有重要作用。

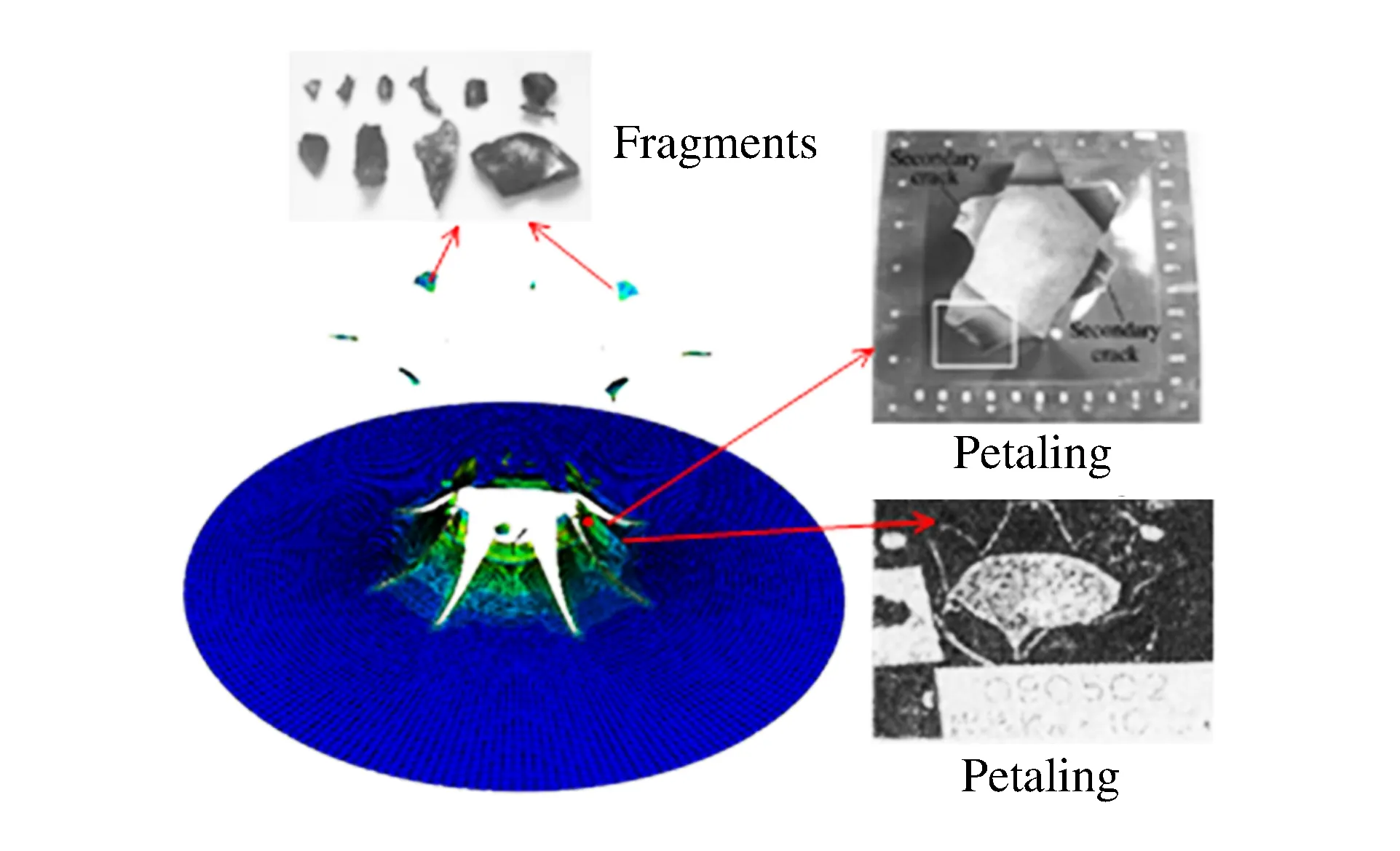
图8 薄板形成的花瓣与碎片Fig.8 Petaling and fragments from the thin pate

图9 等效塑性应变准则获得的破坏模式Fig.9 Failure mode with equivalent plastic strain criterion

4 结 论

花瓣型破口是最基本的爆炸破坏模式之一，仅依据单轴受拉或双轴受拉应力状态开展计算分析，会造成破坏机理揭示不准确。通过开展船用钢材料断裂特性实验，基于多轴应力状态下的舰船用钢失效准则，对局部冲击载荷作用下花瓣型破口的形成过程、各典型位置受力状态、损伤特性等进行了分析。得到以下结论：(1)考虑多轴应力损伤的舰船用钢失效准则能有效预测受力状态复杂的花瓣状破口；(2)花瓣型破口的形成主要分为蝶形凹陷、中心区域裂纹扩展、花瓣形成与翻转等3个阶段；(3)花瓣型破口的裂纹区和非裂纹区受力复杂，除早期受拉伸作用外，后期受震荡的压缩和剪切作用，破口预测须考虑应力状态对损伤特性的影响；(4)花瓣形成过程中，第1阶段和第3阶段均匀变形，第2阶段局部损伤迅速形成，花瓣卷曲会造成花瓣根部的二次损伤。

[1] Scheffler D R, Zuka J A. Practical aspects of numerical simulation of dynamic events: material interfaces[J]. International Journal of Impact Engineering, 2000,24(8):821-842.

[2] Jacob N, Nurick G N, Langdon G S. The effect of stand-off distance on the failure of fully clamped circular mild steel plates subjected to blast loads[J]. Engineering Structures, 2007,29(10):2723-2736.

[3] 牟金磊,朱锡,张振华.水下爆炸载荷作用下加筋板变形及开裂试验研究[J].振动与冲击,2008,27(1):57-61. Mu Jinlei, Zhu Xi, Zhang Zhenhua. Experimental study on deformation and rupture of stiffed plates subjected to underwater shock[J]. Journal of Vibration and Shock, 2008,27(1):57-61.

[4] 陈长海,朱锡,侯海量,等.近距空爆载荷作用下固支方板的变形及破坏模式[J].爆炸与冲击,2012,32(4):368-375. Chen Changhai, Zhu Xi, Hou Hailiang,et al. Deformation and failure modes of clamped square plates under close-range air blast loads[J]. Explosion and Shock Waves, 2012,32(4):368-375.

[5] 陈长海,朱锡,侯海量,等.近距空爆载荷作用下双层防爆舱壁结构抗爆性能仿真分析[J].海军工程大学学报,2012,24(3):26-34. Chen Changhai, Zhu Xi, Hou Hailiang, et al. Numerical analysis of blast resistance of double-layer bulkhead structures subjected to close-rang air blast[J]. Journal of Naval University of Engineering, 2012,24(3):26-34.

[6] Bao Y, Wierzbicki T. On fracture locus in the equivalent strain and stress triaxiality space[J]. International Journal of Mechanical Sciences, 2004,46(1):81-98.

[7] Li Xiaobin, Li Ying, Zheng Yuanzhou. Influence of stress wave on dynamics damage character of ship-build low-carbon steel based on low-velocity Taylor impact bar[J]. Journal of Ship Mechanics, 2014,18(12):1495-1504.

[8] Bao Y, Wierzbicki T. On the cut-off value of negative triaxiality for fracture[J]. Engineering Fracture Mechanics, 2005,72(7):1049-1069.

[9] 金属材料室温拉伸试验方法:GB/T 228-2002[S].北京:中国标准出版社,2002:1-38.

[10] 刘敬喜,崔濛,龚榆峰.船舶碰撞仿真失效准则比较[J].中国舰船研究,2015,10(4):79-85. Liu Jingxi, Cui Meng, Gong Yufeng. A comparative study of failure criteria in ship collision simulations[J]. Chinese Journal of Ship Research, 2015,10(4):79-85.

[10] Bai Y, Wierzbicki T. A new model of metal plasticity and fracture with pressure and Lode dependence[J]. International Journal of Plasticity, 2008,24(6):1071-1096.

[11] 李营.液舱防爆炸破片侵彻作用机理研究[D].武汉:武汉理工大学,2014:23-24.

[12] Nurick G N, Radford A M. Deformation and tearing of clamped circular plates subjected to localized central blast load[C]∥Recent Developments in Computational and Applied Mechanics. Barcelona, 1997:276-301.

(责任编辑 张凌云)

Mechanism research of thin plate petaling under local loading based on multiaxial stress damage

Li Ying1,2, Wu Weiguo1, Zhang Lei2, Du Zhipeng2, Zhang Wei2, Zhao Pengduo2

(1.SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,Hubei,China;2.NavalAcademyofArmament,Beijing100161,China)

A failure criterion considering multiaxial stress state was proposed based on the thin plate damage testing. According to the evaluation of the stress state variation and damage level of the cracking and non-cracking areas, the following conclusions can be reached: (1) the petaling phenomenon of the thin plate used for naval ships can be forecasted effectively by the proposed failure criterion; (2) the petaling procedure can be divided into three distinct stages consisting of butterfly depressing, central area cracking, and petal processing; (3) the stress states of the cracking area and the non-cracking area are complicated, and the stress state’s influence on the damage characteristics should be considered in predicting the petaling crevasse; (4) during the petaling, the central area will sink homogeneously, the cracking will result in large local deformation, and the petal cusps’ curve will lead to a secondary damage to the petal roots.

petaling; stress triaxiality; stress state; failure criterion

10.11883/1001-1455(2017)03-0554-06

2015-09-17；

2016-05-22

国家自然科学基金项目(51509196);中央高校专项基金项目(2014-yb-20); 非线性力学国家重点实验室开放基金项目(LNM201505)

李 营(1988— )，男，博士研究生; 通信作者: 张 磊,freda_zl@126.com。

O346.5;U668.2 国标学科代码： 13015

A