内空和充水管道在爆炸冲击荷载下的数值模拟分析

房 冲

(解放军理工大学，江苏 南京 210007)



·水·暖·电·

内空和充水管道在爆炸冲击荷载下的数值模拟分析

房 冲

(解放军理工大学，江苏 南京 210007)

利用ANSYS/LS-DYNA有限元软件,根据实验目的建立了计算模型，并选取适当的本构关系和材料，对空中TNT炸药爆炸冲击荷载下的内空和充水管道的动力响应规律进行了数值模拟分析，指出爆炸冲击荷载下，在等量炸药的条件下，充水管道的变形量、单元位移及单元压强峰值较内空管道低，这些参数的增加速率也均低于内空管道；充水管道的抗变形能力更强，稳定性更高。

爆炸冲击，充水管道，动力响应，计算模型

0 引言

目前，工程埋地管线的试验研究和模拟计算比较多，针对空爆条件下管道的研究较少。充水管道(充水管)和内空管道(内空管)在空中爆炸冲击荷载下的动力响应是一个重要的研究方向。Ma等[1]对金属管道在内充水条件下受到的冲击进行实验，认为管道中内充水可耗散部分冲击能量，同时提高管道的初始破裂临界速度。纪冲等[2]通过对充液及内空圆柱壳在爆炸冲击下的动力响应和屈曲特性进行了实验和模拟，表明充液圆柱壳在抗爆炸冲击方面较内空圆柱壳提高很大。内空和充水管道在爆炸冲击荷载下的动力响应及变化规律还有待研究。目前，此类问题大多采用有限元方法来求解，可利用ANSYS/LS-DYNA软件对管道在空中爆炸冲击荷载下的动力响应进行数值模拟[3,4]。

1 材料模型及状态方程参数

数值模拟采用ANSYS/LS-DYNA软件中的材料模型及相应状态方程。

1.1 空气、水材料模型及状态方程

空气及水均采用提供的空白材料模型，空气的状态方程为：

P=(γ-1)ρe0/ρ0

(1)

其中，γ为绝热指数，γ=1.40；e0为气体比内能，e0=0.25 MPa；ρ0为空气初始密度,ρ0=1.25×10-3g/cm3。水的状态方程[5]为：

(2)

其中，C,S1，S2，S3，a，E均为相关参数;μ=ρ/ρ0-1;C=1 480 m/s，S1=2.56，S2=1.986，S3=0.00，γ0=0.50,a=0.00。

1.2 炸药材料模型及状态方程

TNT炸药采用高能炸药模型及JWL状态方程，爆轰产物压力P表示的JWL状态方程[6]为:

(3)

其中,V为相对体积;ρ为炸药密度;E0为单位体积炸药内能；A，B，R1，R2，ω均为相关参数。TNT炸药及JWL状态方程参数为:ρ=1 640 kg/m3，E0=7.0×109J/m3,A=374 GPa，B=3.23 GPa，R1=4.15，R2=0.95，ω=0.30。

1.3 管道材料模型

管道选用X70钢材料，采用弹塑性模型，该模型遵从Von-Mises屈服准则[7，8]，其表达式为：

(4)

其中，σ为应力;E为弹性模量;Et为切线模量;σe为屈服应力;ε,εe分别为应变和弹性极限应变。物理力学参数为：ρ=7 830 kg/m3，ω=0.30，E=3.23 GPa，σe=289 MPa，Et=500 MPa。

2 管道动力响应计算模型

建立管道动力响应的计算模型。设坐标轴原点O点为管道中心，X轴为水平方向，Y轴为竖直方向，Z轴与管道轴中心轴向重合且向外为正方向。模型各材料位置如图1所示，管道内分别充水和空气两种介质。

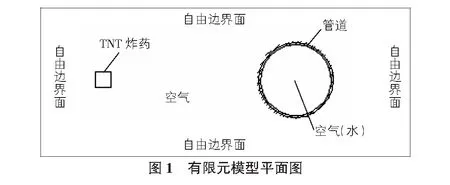
该模型共进行8种工况下的模拟计算，分析充水管道在不同炸药量爆炸冲击荷载下的动力响应问题，各工况编号及详细参数如表1所示。

表1 模型参数表

TNT炸药、空气、水和管道均采用Solid164六面体网格进行划分，炸药、空气、管道内部空气(水)采用ALE算法，管道选择采用LANGANGIAN算法。选用流固耦合方法，将炸药、空气和管道内部空气(或水)与管道耦合在一起进行模拟计算[9]。

3 模拟计算结果与分析

利用ANSYS软件对所建立的模型进行模拟计算，得到管道在空中爆炸冲击荷载下的数值模拟结果。

3.1 管道模拟结果与分析

通过LS-PrePost软件查看工况3和工况7的模拟结果，最终变形如图2所示。

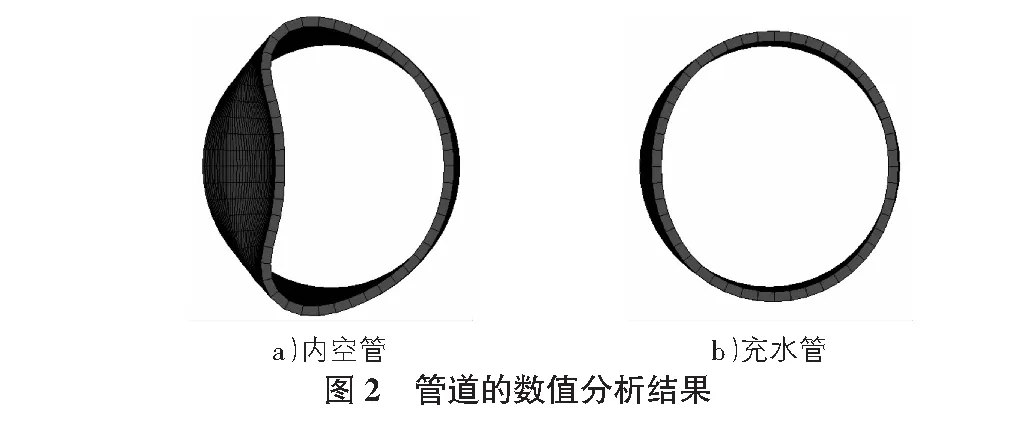
显然，充水管道的变形远小于内空管道，这说明：在爆心距一定的条件下，管道内部的水介质对抵抗管道在爆炸冲击荷载下的变形有很大的作用。

3.2 管道位移过程与分析

在截面上选取4个单元，单元编号及单元位置如图3所示。

以工况3为例，分别做出四个单元合位移时程曲线，如图4所示。

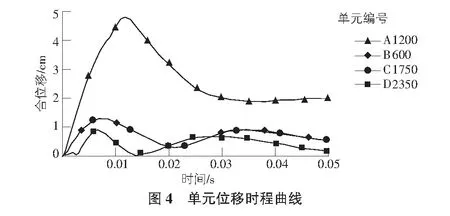
由图4可知：位移先是快速增长，在0.012 s处达到峰值4.83 cm，接着缓慢下降，在2 cm左右达到稳定，这说明：管道已经产生了塑性变形，不能完全恢复。

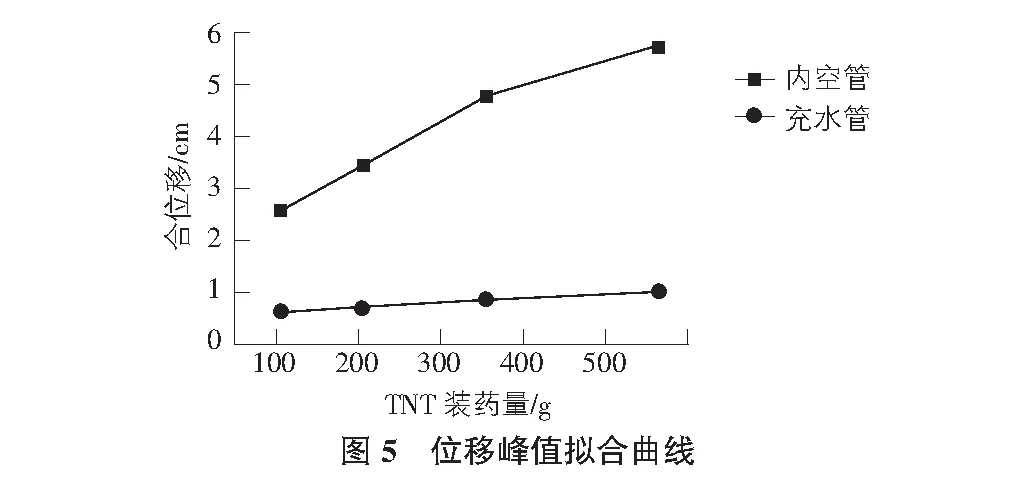
图5为两组模型的单元位移峰值的拟合曲线。由图可知：在等量TNT炸药爆炸冲击荷载作用下，充水管的单元位移峰值不到空管的1/4；炸药量由104.96 g增加到562.52 g，空管单元位移峰值由2.57 cm增加到5.75 cm，充水管单元位移峰值仅增加了0.38 cm，空管的单元位移随炸药增加的速率是充水管的9倍。这说明：充水管单元位移峰值受炸药量变化的影响远小于空管。由于水介质的不可压缩性，在一定程度上削弱了管道受到的冲击荷载，管内空气介质的削弱作用远小于水介质，因而管道内充水能显著降低管道的位移，充水管稳定性高于空管。

3.3 管道压强过程与分析

通过模拟计算出管道在爆炸冲击荷载下的压强，分析8种工况下压强可知：在炸药量一定的情况下，空管压强变化差值大于充水管的压强变化差值，充水管的压强作用时间比空管长；同时，可得到管道在各工况下的峰值压强，其中，迎爆面的单元峰值压强最大，背爆面压强变化最为剧烈，上下两端的压强较为平稳。

通过分析8种工况下的峰值压强可得压强峰值拟合曲线，如图6所示。

由图6可知：在等炸药量的条件下，空管单元压强峰值较充水管高；随着炸药量的增加，空管的单元压强峰值增长速率高于充水管，这说明：管道内部充水对其在爆炸荷载下受到的压强影响较大。

4 结语

1)空管在爆炸冲击荷载下的变形较充水管要大。内部充水情况下，管道的抗变形能力显著提高。2)在等量炸药爆炸冲击荷载下，空管的单元位移峰值远大于充水管；随着炸药量的增加，空管的单元位移峰值增加速率高于充水管。管道充水能有效降低管道的单元位移峰值及位移峰值增加速率，增强管道的稳定性。3)管道压强峰值出现在管道迎爆面上，在等量炸药爆炸冲击荷载下，空管的压强峰值增加速率高于充水管，管道内充水对管道的压强峰值影响较大。

[1] Ma X Q,Stronger W J.Spherical missile impact and perforation of filled tubes[J].International Journal of Impact Engineering,1988,3(1):1-16.

[2] 纪 冲,龙 源,刘 影,等.充液及内空圆柱壳在爆炸荷载下动力屈曲特性研究[J].振动与冲击,2014,33(2):76-80,88.

[3] 钱七虎，王明洋，赵跃堂.爆炸波作用下三相饱和土中不动障碍物上的荷载[J].爆炸与冲击,1994,14(3):97-104.

[4] 赵长啸，龙 源，纪 冲,等.土中爆炸冲击作用下埋地管道动力响应数值模拟研究[J].综述与爆破理论，2010(3)：45.

[5] 李晓杰，张程娇，王小红，等.水的状态方程对水下爆炸影响的研究[J].工程力学,2014,31(8):46-53.

[6] 王 辉.炸药爆炸产物JWL状态方程参数数值计算[D].西安：西安工业大学，2011.

[7] 都的箭，梁雪莹，邓正栋，等.埋地管线爆炸地冲击作用下解析解计算研究[J].爆破,2011,28(3):21-25.

[8] 杨 政，郭万林，董惠茹，等.X70管线钢静态和动态韧性试验研究[J].西安交通大学学报,2003,37(5):488-491.

[9] 姚安林，赵师平，么惠全，等.地下爆炸对埋地输气管道冲击响应的数值分析[J].西安石油大学学报,2009,31(4):168-172.

1009-6825(2017)11-0130-03

2017-02-08

房 冲(1991- )，男，在读硕士

O383.1

A