运用复变理论求解矩形洞室时复变转化函数的修正

杨 峰

(上海理工大学环境建筑学院，上海 200093)



运用复变理论求解矩形洞室时复变转化函数的修正

杨 峰

(上海理工大学环境建筑学院，上海 200093)

介绍了平面弹性复变理论知识，针对求解矩形洞室在采用该理论中保角转化函数精度的不足，对保角转化函数引入修正因子，提高了在复平面转化时矩形洞室截面转化函数的计算精度。

矩形洞室，复变函数，保角转化函数，修正因子

目前国内外的研究大多基于Savin(1961)[1]在其著作中系统阐述平面场中各类孔洞的应力场和位移场问题。由于圆形和椭圆形孔洞的复变函数求解，在进行保角转化时是由有限项组成的精确的映射转化函数，因此在进行转化时是准确的。而对于矩形洞室只能通过截取泰勒级数有限项求出实际洞室的近似映射函数，因此有必要对转化函数进行修正，以此来提高解析解的精度。对于地下矩形洞室，大多采用求近似的映射函数。刘宏才[2]采用梅林契耶夫方法，将作图与计算结合交叉使用，求解出多种常用地下巷道的映射函数，但计算精度不高。范广勤等(1993)[3]采用多角形法去逼近拱形直墙洞室，得到了一个近似洞室边界形状的映射函数，但此法不能满足隧洞形状的多样性。皇甫鹏鹏(2011)[4]通过搜索边界映射点的方法，推导出了求解映射函数表达式系数的新解法。祝江鸿等(2014)[5]在黎曼存在定理的基础上，获得了以洛朗级数有限项表示的单位圆外域到任意形状断面洞室外域的映射函数。因此本文主要针对复变理论中保角转化函数精度不足，引入一个修正因子，从而来提高在由实平面向复平面转化时矩形洞室截面表示函数的精度，最终得到较高精度的映射转化函数。

1 平面弹性复变理论

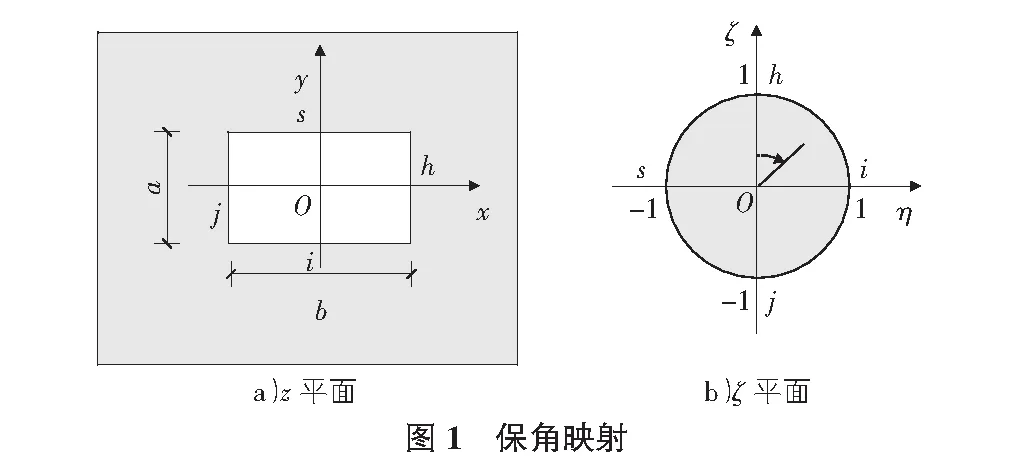
通过保角变换，把z(z=x+iy)平面上矩形洞室外的区域变换

成为ζ平面上以原点为圆心单位圆内域如图1所示。该洞室域的边界线变换为单位圆圆周线，ζ在该复平面上对应表示成式(1)；当ρ=1时，表示矩形洞室上的所有点转化为单位圆圆周上的所有点。因此ζ平面上任一点用极坐标表示为：

ζ=ρeiθ=ρ(cosθ+isinθ)

(1)

矩形洞室的准确映射函数由无限项组成，因此对应的保角转化函数一般形式可以表示为式(2)[1]：

(2)

α=e2kπi

(3)

(4)

(5)

其中，R0一般为复数，在洞室孔口为轴对称时为正实数，同时洞室对孔口尺寸的大小有决定作用；b和a分别为矩形洞室的长和宽(b≥a)；λ为矩形洞室长b与宽a的截面比率，此处为恒不小于1的数值；k与截面比率有关。

2 保角转化函数的修正

将式(3)～式(5)代入式(2)，由欧拉公式合并整理可知，保角转化函数可以表示成为关于λ的表达式，如式(4)所示。式(4)在其项数趋于无穷多项时，将图1a)中矩形洞室外的无限域部分映射到图1b)中的单位圆圆域内，此时映射函数是准确的，不存在误差。但是实际计算时只能选取有限项，这时得到的结果虽然仍是函数形式，但是只能是近似解。如果映射转化函数截取有限项数时，矩形洞室在角点处并非直角而是圆角，并且随着ζ次幂项的递增，圆角会缓慢趋近于直角。

(6)

其中:

在实际应用式(6)时，一般截取保角转化函数的前四项：

(7)

通过式(7)将含有一个近似矩形洞室的无限体实平面映射到一个复平面的单位圆内部。特殊的时候有，当ρ=1时，则ζ=cosθ+isinθ，然后结合式(7)根据复数实部与虚部相互对应可以求得：

x=R0(cosθ+A0cosθ+B0cos3θ+C0cos5θ)

(8)

y=R0(-sinθ+A0sinθ+B0sin3θ+C0cos5θ)

(9)

取ζ平面上h(θ=0时)点值对应于z平面上矩形洞室长b的1/2，即：

(10)

同样的有，取ζ平面上s(θ=-π/2时)点值对应于z平面上矩形洞室宽a的1/2，即：

(11)

联立式(10)和式(11)两式，可以得到转化后的矩形洞室截面比率如下所示：

(12)

同时由式(10)可知：

(13)

整理式(13)得到：

(14)

由于λ恒为不小于1的数值，结合式(12)可以得到以下结论：在截取映射函数前四项时，初始截面比率恒小于映射转化后的截面比率。同时知道矩形洞室映射转化函数的系数与形式是明确的，因此可以通过对转化函数中独立变量λ进行修正来达到提高转化函数精度的目的。此时修正因子f引入后，可以表示如下：

(15)

相应的有，修正后的映射转化函数表示如下：

(16)

其中：

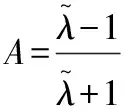
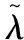
(17)

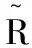
(18)

(19)

对于修正后的保角转化函数，类似的可以得到：

(20)

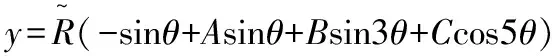
(21)

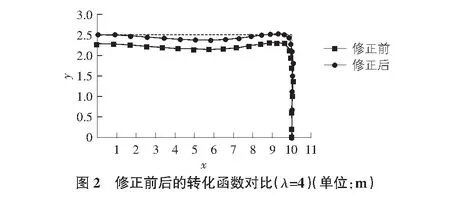
根据式(8)与式(9)绘制图2中修正前转化曲线，根据式(20)与式(21)绘制出图2中修正后转化曲线。由于矩形洞室的对称性，此处选取矩形洞的1/4来进行研究，假定矩形洞室长度b取20 m，宽度a取为5 m。通过图2可以发现，保角转化函数修正前由于仅截取其前四项，导致求解的矩形洞室截面尺寸与初始矩形洞室截面尺寸存在较大误差，而引入修正因子后的修正转化函数的截面尺寸与真实矩形洞室截面尺寸大大接近，转化精度得到明显提高。

3 结语

针对求解矩形洞室在采用复变理论中保角转化函数精度的不足，通过引入一个修正因子，从而提高了映射转化函数的转化精度，达到了对映射转化函数进行修正的目的。

[1] Savin G N.Stress concentration around holes[M]. London,UK:Pergamon Press,1961.

[2] 刘宏才.巷道断面形状对弹性围岩力学状态的影响[D].泰安:山东矿业学院,1987.

[3] 范广勤,吴 汎.应用三个绝对收敛级数相乘法解非圆形洞室的外域映射函数[J].岩石力学与工程学报,1993,12(2):81-82.

[4] 皇甫鹏鹏,张路青.基于高效保角变换的单个复杂洞室围岩应力场解析解研究[J].岩石力学与工程学报,2011,31(S2):3899-3901.

[5] 祝江鸿,杨建辉.单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J].岩土力学,2014,33(1):176-184.

Modification of complex transformation function of rectangular cavity with complex variable theory

Yang Feng

(SchoolofEnvironmentandArchitecture，UniversityofShanghaiforScienceandTechnology，Shanghai200093，China)

The paper introduces horizontal elastic complex theories. In light of conformal conversion function accuracy failure applied in solving rectangular cavity, the correction factor of the conformal transformation function is introduced to improve the calculation accuracy of the cross section conversion function of the rectangular tunnel.

rectangular cavity, complex function, conformal transformation function, correction factor

1009-6825(2017)11-0060-03

2017-02-07

杨 峰(1988- )，男，在读硕士

O174

A