基于BP神经网络的汽车车载称重系统研究∗

秦 伟，徐国艳，余贵珍

(北京航空航天大学交通科学与工程学院，北京 100191)

基于BP神经网络的汽车车载称重系统研究∗

秦 伟，徐国艳，余贵珍

(北京航空航天大学交通科学与工程学院，北京 100191)

为解决汽车超载运行和相应的运输业管理问题，本文中提出了一套基于BP神经网络的车载称重系统。通过检测车桥随载荷量变化而产生的微小变形，设计了2阶低通滤波和数字滤波算法，以提取有效载荷信息，利用BP神经网络建立载荷模型，并根据在某轻型厢式货车上进行的试装和加载试验得到的样本数据，在Matlab神经网络工具箱中，采用Levenberg-Marquardt学习算法完成了神经网络的学习、检验和预测。结果表明：预测载荷误差在5%以内，满足工程要求，方案可行。

车载称重系统；低通滤波；BP神经网络；Levenberg-M arquardt学习算法

前言

车辆超载问题是困扰交通安全的重大问题之一，据统计，70%的道路安全事故是由于车辆超限超载引发的，不但数量庞大，且破坏性严重[1]。目前，解决超载问题的途径，除加强执法力度外，动态称重系统(weighing-in-motion，WIM)技术发展较快，它允许汽车以一定的速度通过检测区，实现不停车称重，提高了检测效率，精度较高[2-4]，但却仍属于定点称重策略，无法解决更广泛的超载问题。为从源头上治理超载，人们着眼于货运汽车本身，加上近年来无线通信技术的飞速发展，将称重装置安装在汽车车体上的车载称重技术正引起人们越来越多的重视。而对于运输业来说，车载称重系统有利于提高运输效率，并防止驾驶员的不正当行为。

目前的车载称重系统的研究具有3个主要分支。第1种是直接法，将传感器安装在车架和货箱之间，传感器组承受全部载荷，这对传感器本身的工艺要求较高，丹麦Eilersen公司的产品就属此类；第2种是间接法，车梁、车桥和悬架等车身结构件受载后，会产生相应的弹性变形，通过检测和采集这些信息并转换为载荷信息，这种方法对车辆本身承载结构的影响甚微，没有安全隐患；而像城市垃圾车、餐厨车和装载机等具有专门的提升和装载机构的车辆，可通过对载质量的变化状况进行跟踪，以实现总载荷的测量，则属第3种方法。

本文中采用的称重策略将传感器安装在车桥上，当车辆载重时，车桥产生相应的微量变形，利用传感器采集该信号，采集到的数据经过滤波、转换、神经网络算法等处理后得到载货量信息。按照此方法，在设备安装时只须进行少量焊接，对车桥的承力结构造成的影响甚微，不会影响车辆行驶的安全性，属于间接测量的第2种方法。

1 车载称重系统的设计

静止工况下的数据采集是称重的重点，而判断静止工况最直接且准确的物理量就是速度，故而应当设置速度作为参考量。另外，在长期使用过程中，疲劳和机械蠕变等外部因素，会对传感器产生不可逆的干扰，这些非随机性的干扰难以通过常规的滤波算法进行去除，所以，在数据处理，尤其是数据截断的过程中，应当对作为参考的初值进行不断修正。该称重系统的工作流程如图1所示，当汽车从行驶工况转为静止工况时，系统对传感器的即时值进行读取并锁定，然后基于此值执行后续的称重算法，而当汽车从静止工况转为行驶工况时，传感器初值将再次记录并锁定载荷数值。

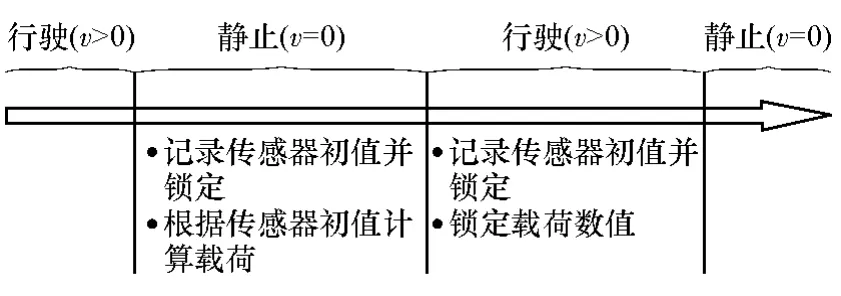
图1 车载称重系统工作流程

1.1 硬件系统设计

车载称重系统是一套集成数据的采集、传输、融合和呈现等功能为一体的数据处理系统，其构成如图2所示。

对于称重问题，目前，广泛应用的传感器有位移式、电容式和应变式3种类型，选型时主要考虑的因素有精度、可靠度、成本和安装难易度等，综合考虑上述因素，采用了应变式传感器。这种传感器在称重领域使用时间较长，技术成熟，若采用多片应变片组成惠斯通电桥，可实现温度的自行补偿。此外，它还具有150%的过载能力，由于是安装在车桥上，车辆的主要载荷由车桥承受，传感器自身不承载，故过载能力满足要求。

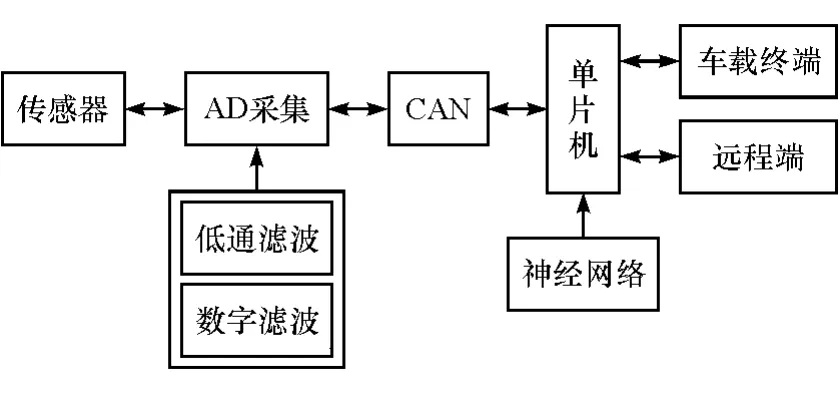
图2 称重系统构成与流程图

传感器采集到的数据经过低通滤波和数字滤波，完成初步处理。考虑到车辆轴数会随车型的不同而发生变化，而CAN总线上节点接入方便，可有效提高系统对不同车型的适应能力，故选取CAN总线网络完成传感器与单片机间的数据传输。搭载STM32型单片机的控制板接收到数据后，经过BP神经网络处理，将数据转换成载荷信息。之后，载荷信息被显示在车载终端上，另外，主控板上还留有移动数据接口，以实现数据的远程传输。

1.2 滤波算法设计

受到地面不平度、车辆自身谐振、货物装卸时冲击引起的振动等因素的影响，实际数据采集中会混入大量干扰成分，影响采样结果，根据文献[5]，干扰信号大多为高频信号，车辆的载重信号则为低于20Hz的低频信号，故应采用低通滤波算法对采样信号进行处理，消除高频干扰，提高数据采集的可靠性。

1阶低通滤波器存在输出电压在高频段下降速度较慢的问题，而2阶低通滤波可解决这一问题[6-8]，故而采用2阶压控低通滤波电路，其电路结构如图3所示。

图3所示电路的传递函数为

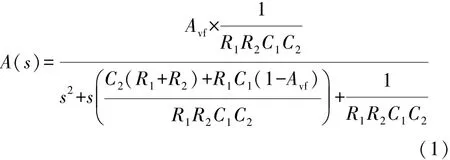
式中：Avf为通带增益。

特征角频率为

图3 压控型2阶有源低通滤波基本结构

为方便元件选取，取电阻值R1＝R2＝R，电容值C1＝C2＝C，由fc＝1/(2πRC)，截止频率为fc＝20Hz，则C＝10μF，进而R＝795.8Ω，根据0603型贴片电阻阻值，取最接近的R＝820Ω，由等效品质因数Q＝为使Q为理想的0.707，可得Avf≈1.59，取为1.6，则R4/R3＝0.6，取R3＝1kΩ，R4＝1.6kΩ。

用Multisim9仿真软件对滤波电路进行模拟搭建和仿真，搭建的仿真电路如图4所示。

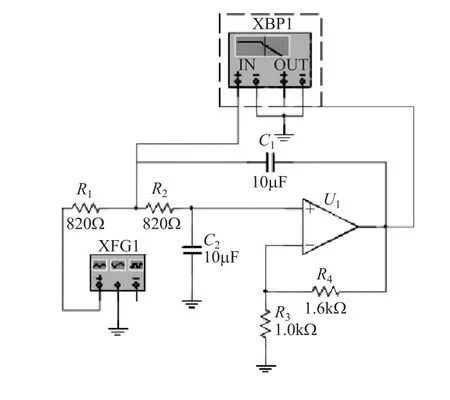
图4 Multisim9仿真电路

仿真结果如图5所示。由图可见，曲线的纵坐标最大值为8.24dB，按照-3dB截止频率，图中已将标尺移动至5.21dB处，此时的频率f＝19.765Hz，符合设计要求，达到了预期效果。

数字滤波部分采取中位值平均滤波算法，连续采集10个数据Xi，i＝0～9，然后对这10个数据进行排序，去除最大值和最小值，然后对剩下的8个数据取平均值作为本次采集的有效数值Y，同时将Y值发送到MCU。这种方法可有效克服因偶然因素引起的脉冲性波动干扰而引起的偏差值。另外，还可减小总线上的数据传输压力。

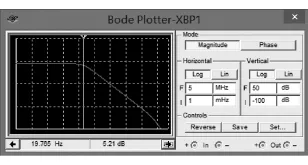
图5 Multisim9仿真结果

2 载荷模型的建立

载荷模型的优劣直接关系到整个系统的性能，是数据处理中要解决的关键问题。涉及到力和变形时，一般考虑动力学分析或静力学分析的建模方法，其中，动力学分析往往把分析对象简化为弹簧阻尼系统，建立相应微分方程作为分析模型；静力学分析则要求充分掌握分析对象的形状参数和材料力学性能参数，才能达到良好的效果。而车桥本身是一个形状和结构都很复杂的汽车结构件，无论三维建模还是台架试验测量，动力学中的弹簧刚度、阻尼系数，或静力学中的扭转刚度、弯曲刚度等参数都难以获得；另外，不同车型的车桥形状大小各异，每当车桥改变，这些工作都要重新来做，更是费时费力，实际效果如何也难以定论。所以，动力学或静力学的分析方法都不太适用，本文中采用了神经网络模型来进行载荷模型的建立。

BP神经网络在函数逼近、模式识别等众多领域应用广泛，其输入与输出之间是一种高度非线性的映射关系，只要合理设置输入节点数N，输出节点数M和隐层节点数H，调整神经网络的连接权值，则可以任意的精度逼近一个非线性函数[9]。即通过实车样本数据对神经网络进行训练，使各节点的权值参数收敛到理想数值，并用另一部分试验数据对神经网络进行验证和预测，使性能达到精度要求。这样不但可避免其他建模方法中物理模型建立困难的问题，还会因样本来自真实试验，相当于把其他方法中忽略掉的因素也考虑到，而提高了建模的准确性。

但要说明的是，网络的输入采用的不是力或者变形，而是传感器采集到的AD值，由于AD值跟变形量正相关，二者本质上一致，仅相差一个换算系数。

进行BP神经网络设计时，首先要完成其拓扑结构的确定，神经网络由输入层、输出层和隐含层构成，输入层节点N为多路应变式传感器采集到的AD数据，由于试验车为两轴轻型货车，故取N＝4。网络输出为载荷量，故M＝1。

隐层数和隐层节点数是网络设计中的一个重要问题，数目增多会对精度有益，却会导致网络泛化能力下降，训练要求的数据增长，训练时间变长，而过少的隐层数会导致隐含层连接权值数目变少，网络的识别性和拟合性变差[10]。对此，尚没有一个良好的解析式，目前主要通过与被逼近函数的符合程度，以及目标精度等因素进行初步估计，再根据效果逐渐优化，但比较来看，增加隐节点数的方法在提高网络的性能方面相对来说更加有效，故实际往往优先采用3层神经网络，即单一隐层。而关于隐节点数，有些经验公式可初步估计隐节点数，文献[11]中提供了如下几种计算公式：

其中：a＝1～10

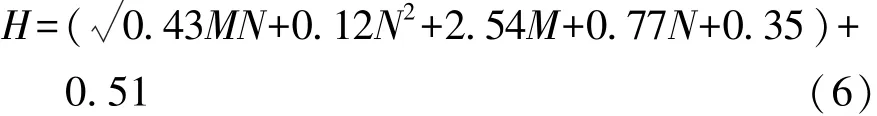
式(4)～式(6)综合考虑了输入与输出节点的影响，本文中采取式(6)，计算可得H＝3.61，初步选定隐层节点数为H＝4。

3 训练样本采集

3.1 设备实车安装与加载试验

所设计的车载称重系统安装在江淮康铃厢式轻型货车上进行加载试验，试验车外观如图6所示，额定载荷2t，轴距2.8m，前轴轮距1.7m，后轴轮距1.6m。

图6 试验车外观

所用加载重物为混凝土路牙石块，优点是形状规则，易于码放，易于实现位置较为准确的加载，单块质量m约为42kg。

采用文献[12]中传感器的安装方式，如图7和图8所示。图中白色圈中即传感器实物，它通过螺柱安装在车桥上，前轴安装在车桥前侧两端，后轴安装在主减速器两侧，焊接安装螺柱时，间距需要严格控制，只有这样，当传感器预紧至预设数值，各传感器的性能才能保持稳定和一致。另外，左右侧车桥变形的方向有所不同，所以传感器也有左右之分。

图7 前桥传感器安装示意图

图8 后桥传感器安装示意图

加载试验过程中，加载位置选取货厢的正中位置。首先，根据货车2t的额定载质量，以10%作为加载时的步长值，从空载开始，逐级加载至最大值，再逐级递减至空载作为一次完整的试验过程，如此重复一遍作为一天的数据，随后在第2天和一周之后再次进行实车加载试验。排除粗大误差数据后，总共得到117组有效试验数据，用于进一步的BP神经网络训练。

表1为每次试验开始时，空载状态所记录的传感器值。可以看出，传感器数值会产生漂移，且数量级与处理算法中值的数量级相近，对最终结果的影响不容忽视。这主要是由两个原因引起：一是之前所提到的关于初值问题的讨论；二是由于安装时螺栓组预紧的问题，使传感器上存在一定的内应力，这种内应力会随着车辆运行逐渐释放。

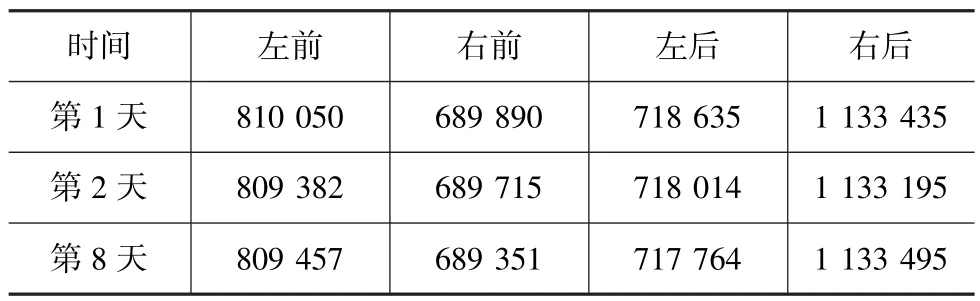
_表1 试验开始时的传感器值(空载)

表2为实际加载时的加载量与AD变化值之间的关系。试验过程中，由于加载组别较多，所以只列出了加载量为额定载荷量的10%，20%，30%，40%，70%和100%时的试验数据。

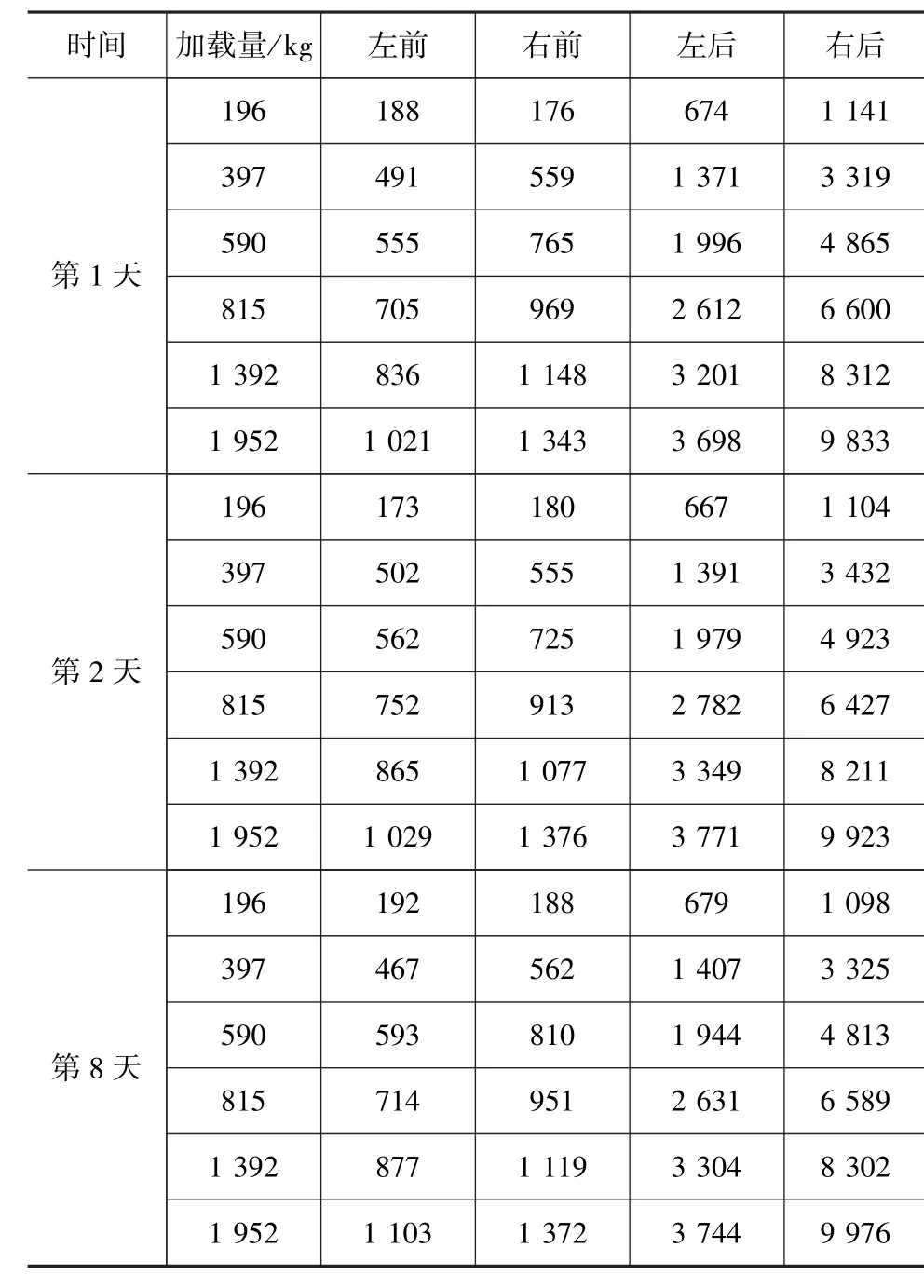
_表2 加载试验数据

3.2 BP神经网络的训练、验证和预测

对BP神经网络进行训练的目标是使网络输出与期望值之间的均方误差MSE达到要求，具体的方法是根据MSE的梯度调整网络参数，再次计算MSE，循环此过程直至满足要求或到达训练退出的其他条件[13-14]。

由表2可知，加载量少和加载量多时的数据最多会相差2个数量级并且从数值角度看，采集的数据较大时，容易在数值计算过程中产生问题。此外，为提高训练的收敛速度，对样本数据进行归一化处理，最后再将结果反归一化。

本文中使用Matlab工具箱对神经网络进行训练，训练过程中，采用批处理训练模式，将所有试验数据导入工作空间，将数据按照70%，15%，15%进行划分，分别用于神经网络的训练、验证和预测。结合本文中网络的规模和单片机的处理能力，训练的学习算法采用Levenberg-Marquardt(LM)算法[15]。它是Gauss-Newton算法的改进，避免求Hessian矩阵，而是用下式来代替。

式中：J为雅可比矩阵。

则

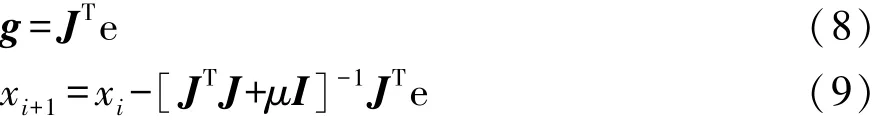
式中：g为梯度；xi为权值和阈值；I为单位矩阵；e为自然底数；μ为调整参数，根据每次的训练结果调整μ值，可加快训练过程。

其他训练参数如表3所示。

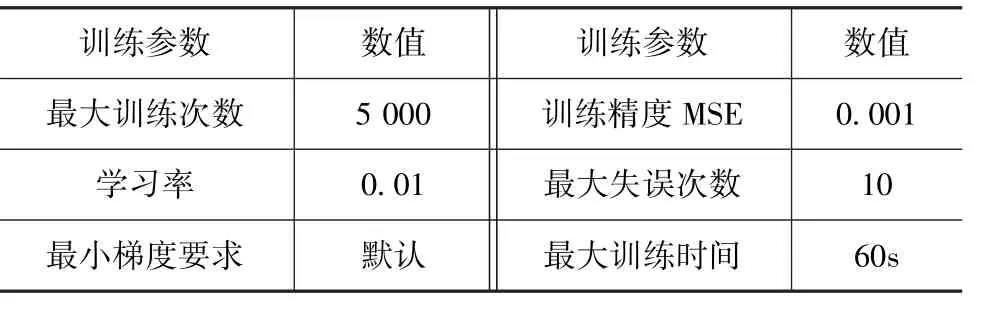
表3 BP网络训练参数设置

开始时，按照初步估计取隐节点数H＝4进行训练，结果如图9所示。

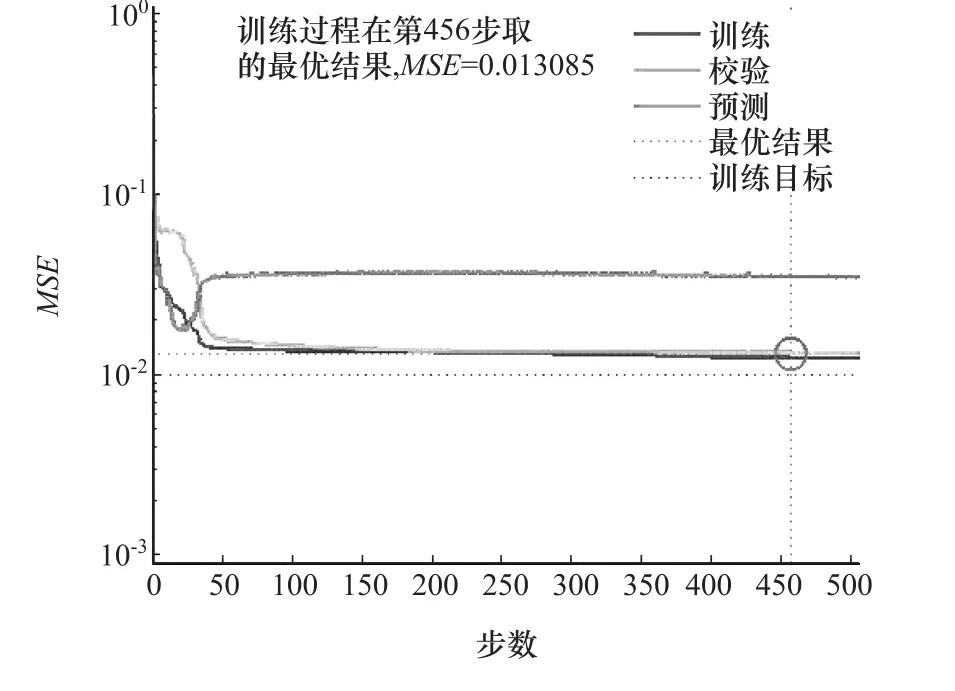
图9 H＝4时的均方误差曲线

由图可见，训练曲线与验证曲线较为一致，而测试曲线效果不理想，于是增加了节点数，当H＝5，6时，结果如图10和图11所示。

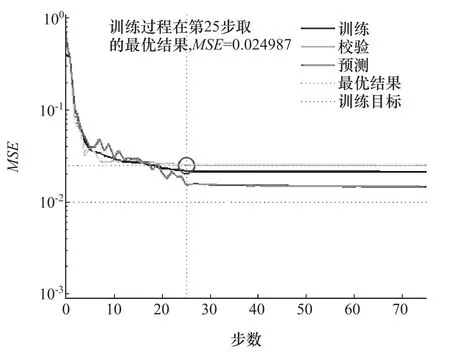
图10 H＝5时的均方误差曲线

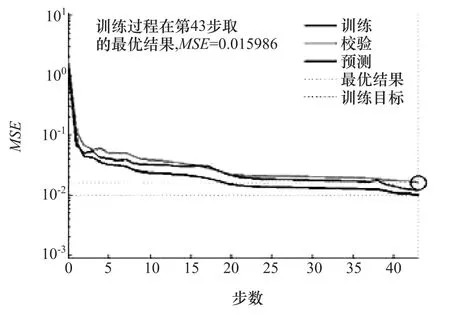
图11 H＝6时的均方误差曲线

由图可见：当H＝5时，训练过程中的最小均方值不理想；当H＝6时，效果比较理想，此时神经网络的拓扑结构为4×6×1。由于Matlab在选取样本时具有随机性，每次训练的结果并不完全相同，需要对神经网络进行多次训练，然后取效果最好的一次参数作为最终的网络参数。

此时，神经网络的权值矩阵Hw如表4所示。

表4 隐含层权值H

图12为对预测过程作回归化，相关系数很高，可见预测过程中，输出对实际值的跟踪效果较好。

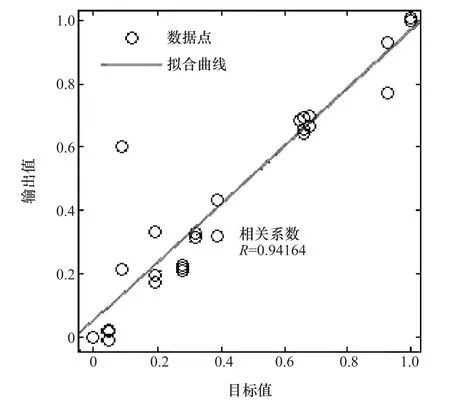
图12 校验过程回归

表5为称重预测的结果，可见当质量较小时误差相对较大，随着载荷增加，性能逐渐变好，原因是由于汽车本身质量较大，结构复杂，不同构件之间存在着间隙和内力，使系统在载荷较低时灵敏程度稍低，而当质量达到一定程度时，系统性能才会变得更稳定。但总体来看，相对误差在5%以内，满足工程设计要求。

表5 称重结果预测

由于试验条件有限，只在一辆车上进行了安装，对于两轴车，不同车型车轴之间刚度会存在差异，但神经网络拓扑结构仍然适用，只需进行少量加载标定即可实现系统移植。

4 结论

完成了车载称重系统软硬件的设计，针对系统运行过程中会受到的随机干扰，设计了压控型2阶有源低通滤波电路和中位值平均滤波算法，并通过使用Multisim9仿真软件对低通部分进行了滤波性能仿真，结果表明，滤波设计满足要求。通过BP神经网络对多路传感器AD值与真实载荷间的关系进行了神经网络建模，构建了4×6×1型3层网络，依靠实车试验样本数据对神经网络进行了训练，确定了各层权值和阈值，从预测结果来看，称重误差可控制在5%以内，满足工程要求。

[1] 洪秀敏.公路超限运输的六大危害[J].中国公路，2002(15)：76-77.

[2] NIEDZWIECKIM，WASILEWSKIA.Application of adaptive filtering to dynamic weighing of vehicles[J].Control Engineering Practice，1996，4(5)：635-644.

[3] KENYON A CH.Practical on-board weigh-in-motion system for commercial vehicles[J].Proceedings of SPIE-The International Society for Optical Engineering，1997，29(3)：156-161.

[4] PHILLIPS，DARRYLH.On-board weigh-in-motion of class8 trucks using Newtons second law[C].SAE International Truck and Bus Meeting and Exposition，1997.

[5] 周良亚.环卫车车载称重计量系统开发[D].上海：华东理工大学，2010.

[6] 桂静宜.二阶有源低通滤波电路的设计与分析[J].电子科技，2010，23(10)：15-17.

[7] LIAO Y C，ZHAO H B，LIU Y J，et al.The design of active low pass filter[J].Applied Mechanics＆Materials，2014，541-542 (10)：419-423.

[8] FOSTER E.Active low-pass filter design[J].Audio IEEE Transactions on，1965，au-13(5)：104-111.

[9] 师洪涛，杨静玲，丁茂生，等.基于小波—BP神经网络的短期风电功率预测方法[J].电力系统自动化，2011，35(16)：44-48.

[10] 沈花玉，王兆霞，高成耀，等.BP神经网络隐含层单元数的确定[J].天津理工大学学报，2008，24(5)：13-15.

[11] 高鹏毅，陈传波，秦升，等.一种新的基于Agent的神经网络隐层节点数的优化算法[J].计算机工程与科学，2010，32(5)：30-33.

[12] 张荣军，罗向东，许晨光，等.基于物联网的车载称重监控系统[J].计算机应用，2014(S1)：320-322.

[13] LIJ，SHENG V S，SHU Z，et al.Learning from the crowd with neural network[C].IEEE，International Conference on Machine Learning and Applications.IEEE，2015.

[14] 傅荟璇.MATLAB神经网络应用设计[M].北京：机械工业出版社，2010.

[15] FUN M H，HAGAN M T.Levenberg-Marquardt training formodular networks[C].IEEE Int.Conf.Neural Networks，1996，6：468-473.

A Research on Vehicle On-Board Weighing System Based on BP Neural Network

Qin W ei，Xu Guoyan＆Yu Guizhen
School of Transportation Science and Engineering，Beihang University，Beijing 100191

To solve the problem of truck's overload running and related transportation management，a vehicle on-board weighing system based on BP neural network is proposed.Bymeasuring the tiny deformation on truck axles caused by load，second-order lowpass filtering and digital filtering algorithms are designed to extract effective load data.Then load model is built by using BP neural network，and according to the sample data obtained in loading test on a light van with weighing system installed，a process of learning，testing and prediction of neural network is completed by adopting Levenberg-Marquardt learning algorithm in Matlab neural network tool box.The results show that the error of predicted load iswithin 5%，meeting engineering requirements and indicating the feasibility of proposed scheme.

on-board weighing system；lowpass filtering；BP neural network；Levenberg-M arquardt learning algorithm

10.19562/j.chinasae.qcgc.2017.05.018

∗国家自然科学基金(61371076)资助。

原稿收到日期为2016年5月27日，修改稿收到日期为2016年7月5日。

徐国艳，副教授，E-mail：xuguoyan＠buaa.edu.cn。