基于多场耦合建模的发动机半主动悬置参数识别∗

郑 玲，犹佐龙，刘巧斌，庞 剑，徐小敏，陈代军

(1.汽车噪声振动与安全技术国家重点实验室，重庆 401120； 2.重庆大学汽车工程学院，机械传动国家重点实验室，重庆 400044；3.重庆长安汽车工程研究院，重庆 401120))

基于多场耦合建模的发动机半主动悬置参数识别∗

郑 玲1，2，犹佐龙2，刘巧斌2，庞 剑1，3，徐小敏1，3，陈代军1，3

(1.汽车噪声振动与安全技术国家重点实验室，重庆 401120； 2.重庆大学汽车工程学院，机械传动国家重点实验室，重庆 400044；3.重庆长安汽车工程研究院，重庆 401120))

针对半主动悬置优化中存在的多场耦合精确建模的难题，采用ADINA软件，建立了半主动悬置液固气三相耦合仿真模型，通过关键参数的辨识和准确提取，获得了半主动悬置的集总参数模型，并研究了其动特性。结果表明：基于ADINA的液固气三相耦合仿真模型，能快速、准确提取集总参数模型的关键参数，实现半主动悬置动特性的准确预测。通过试验验证了多场耦合建模和动特性分析方法的正确性，为汽车发动机半主动悬置的正向开发与结构优化提供了可行的方法。

半主动悬置；液固气三相耦合模型；参数识别；动特性

前言

传统的橡胶悬置由于其较小的阻尼和高频动态硬化效应，已无法满足汽车舒适性的要求。液压悬置的出现弥补了橡胶悬置阻尼过小的缺陷，且刚度____和阻尼具有一定的频变特性，能较好地隔离发动机振动，成为一种重要的结构形式[1]。但液压悬置结构一旦确定，其频变特性也随之确定，不能很好适应汽车复杂运行工况的要求。近年来，半主动悬置由于其良好的工况适应性，成为国内外汽车工程领域的一个研究热点。

半主动悬置是在液压悬置基础上，通过改变液体黏度如磁流变悬置[2-3]或改变结构参数如解耦膜刚度控制式[4]和惯性通道可调式[5-6]来实现其动特性的调节。目前，对半主动悬置动特性的研究大都采用集总参数建模的方法，但如何获得准确的集总参数模型的建模参数，一直是亟待解决的难题。获得建模参数的方法主要有试验法和仿真法两种。文献[7]中采用试验方法，提取了液压悬置的建模参数。文献[8]中利用悬置不动点特性，获取了液压悬置的建模参数。文献[9]中使用特征点法计算出悬置各个参数。以上方法均需要加工液压悬置样件，并进行动特性的测试，不仅使设计周期延长，开发成本增加，且无法直接用于正向开发和结构优化设计。文献[10]中利用液固耦合方法提取了解耦盘式液压悬置的集总参数，文献[11]中采用COMSOLMULTIPHYSCIS软件仿真得到液压悬置中解耦膜的体积刚度，文献[12]中用有限元方法进行了悬置动特性分析，文献[13]中通过建立强液-固耦合有限元模型仿真了悬置动特性，这些有限元仿真方法均针对传统被动液压悬置进行计算，未考虑悬置中空气的作用。而针对本文中的解耦膜刚度控制式半主动悬置，必须考虑悬置中空气的影响，因为空气的体积刚度变化直接决定了上液室的体积刚度变化，导致悬置表现出不同的动态特性。

本文中针对上述问题，采用多场耦合分析软件ADINA，建立解耦膜刚度控制式半主动悬置的液固气三相耦合有限元分析模型，通过该模型来提取集总参数模型的建模参数，对半主动悬置的动力学特性进行准确预测，为发动机半主动悬置的正向开发提供先进的设计方法。

1 半主动悬置工作原理

图1为解耦膜刚度控制式半主动悬置结构示意图。从图1可知，当悬置受到外界低频大振幅激励时，橡胶主簧发生变形挤压上液室液体，受挤压的液体经惯性通道流往下液室，由于惯性通道阻尼作用，液体的振动能量被衰减；当悬置受到外界高频小振幅激励时，由于液体的动态硬化效应，液体几乎不再经过惯性通道，此时主要由变形的橡胶主簧和解耦膜容纳被挤压的液体。

此外，半主动悬置通过侧置的电磁阀控制解耦膜下端空气腔的开闭。若空气腔关闭，气腔内部空气的体积刚度增大，使解耦膜和上液室的体积刚度增大，导致悬置整体表现为大刚度大阻尼特性；若空气腔打开，气腔内部空气自由流动，解耦膜刚度变小，导致上液室体积刚度变小，悬置整体表现为小刚度小阻尼特性。

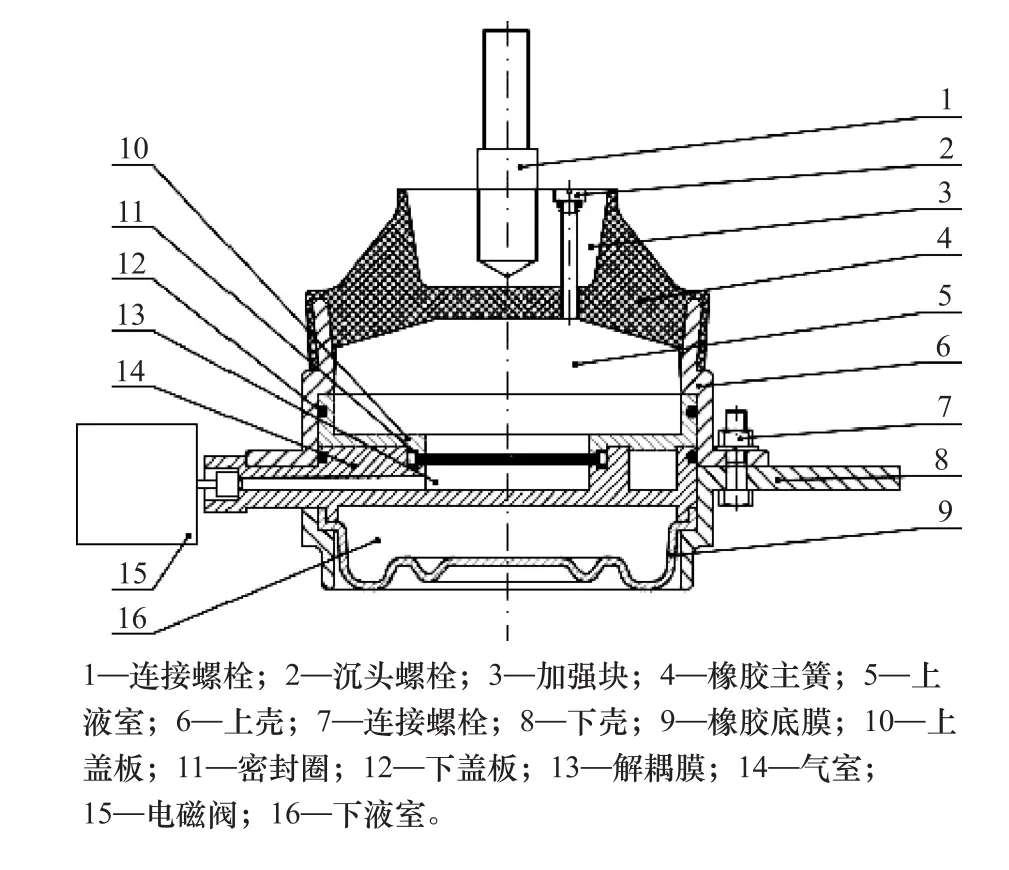
图1 半主动悬置结构示意图

2 半主动悬置集总参数建模

根据半主动悬置结构形式和工作原理，建立集总参数模型，如图2所示。

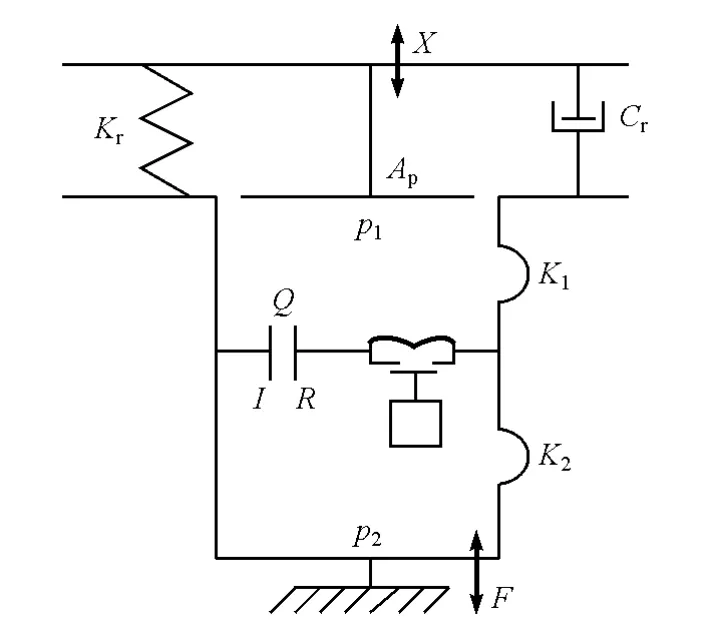
图2 半主动悬置集总参数模型

图中：Kr和Cr为悬置橡胶主簧的动刚度和阻尼系数；Ap为悬置的等效泵压面积；K1和K2为上下液室的体积刚度，其中K1随着空气腔的开闭而改变；p1和p2为上下液室内的压强；Q为惯性通道内的液体流量；I和R为惯性通道内液体的惯性系数和流量阻尼系数；X为作用于悬置上端的位移激励；F为悬置的传递力。

根据流体力学的动量原理：

发动机振动位移引起激励，并经悬置传递到车身或车架上的力为

对式(1)～式(4)进行拉氏变换，合并可得悬置的复刚度为

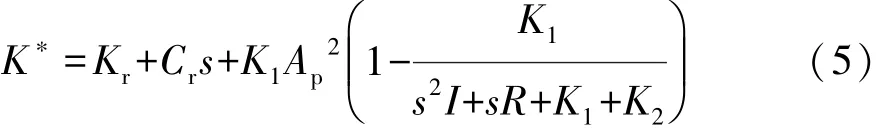
式中s为复变量，s＝j w。

按照定义，悬置的动刚度为复刚度表达式的实部，悬置的阻尼角为复刚度表达式的虚部与实部比值的正切值，即

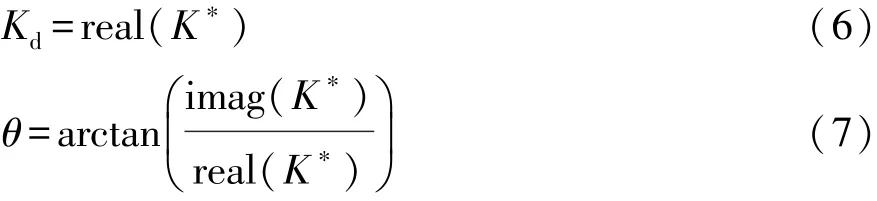
由此可见，对悬置动特性的准确预估依赖于对集总参数模型的重要建模参数如Kr，Cr，Ap，K1，K2，I和R的准确提取。

3 流固耦合理论

件(力平衡)：

传统的液压悬置为消除高频硬化现象，大都采用解耦盘或空气腔密闭的解耦膜进行解耦。采用解耦盘式的液压悬置没有气体影响，采用空气腔密闭的解耦膜式液压悬置气体影响较小，通常使用液固耦合的理论来建立有限元分析模型。针对本文中解耦膜刚度控制式半主动悬置，考虑到空气腔的开、闭带来解耦膜刚度的改变，必须采用液固气三相耦合理论来建立半主动悬置多场耦合有限元分析模型，研究其动特性。

图1所示半主动悬置的液固气三相耦合过程如图3所示。

由图3可见，外界激励施加到橡胶主簧使主簧变形，导致上液室中的液体压力发生变化，而液体的压力变化又使解耦膜发生变形或通过惯性通道流到下液室使橡胶底膜发生变形。如果空气腔关闭，解耦膜的变形将会使空气压缩，导致其体积刚度增大，从而阻止解耦膜的继续变形；如果空气腔打开，解耦膜便可自由变形，不会受到空气压缩产生的阻力。

在计算流固耦合问题时，应用在流固耦合界面的基本条件是运动学条件(位移协调)和动力学条

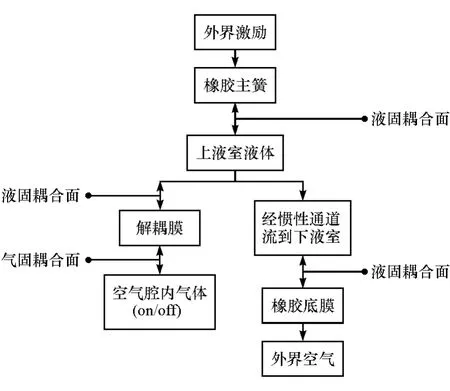
图3 半主动悬置液固气三相耦合示意图

式中：df和ds分别为流体和结构的位移；τf和τs分别为流体和结构的应力；n为单位法向量。流体的速度条件由运动学条件得到，如果应用无滑移壁面条件，则如果是滑移壁面条件，则有

本文中对悬置内液体、气体和橡胶金属件分别进行建模，最后通过耦合面的处理，建立半主动悬置的液固气三相耦合模型，并仿真计算得到悬置的各个集总参数。

4 半主动悬置有限元参数辨识

利用catia和hypermesh对半主动悬置进行建模并划分网格，如图4所示。图中模型经过了简化，考虑到外壳、盖板等一些与液体接触的金属部件是固定不动的，因此将这些部件删除，只需在软件中将这些金属部件与液体的接触面定义为壁面Wall即可。固体和液体网格均采用六面体8节点网格单元，网格尺寸最小为0.95mm，最大为7.21mm，3D网格数量为15 134，2D网格数量为8 725。需要注意的是软件允许流体和结构区域使用不同的网格，但两个模型边界之间的距离必须很小。

图4 半主动悬置有限元简化模型

将建好的有限元模型以nas的格式导入ADINA软件中，便可进行相关参数的仿真计算。

4.1 橡胶主簧静刚度

将悬置的橡胶主簧和加强块网格导入ADINA中，如图5(a)所示。橡胶材料选用Mooney-Rivlin模型，其中C1＝0.3，C2＝0.087。计算时，约束橡胶主簧下端，在加强块中心处施加一个垂向位移载荷，通过提取悬置的作用反力，获得悬置的力-位移曲线如图5所示。

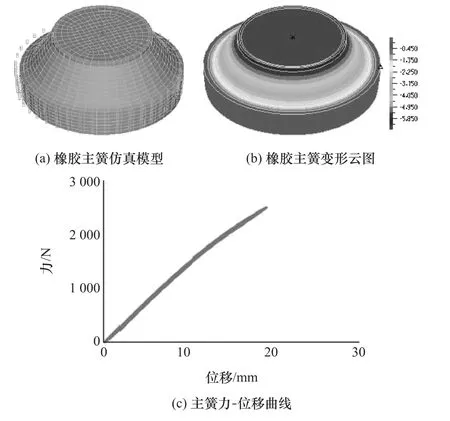
图5 橡胶主簧静特性仿真

由图5(c)可见，悬置的力-位移曲线趋于一条直线，迟滞效应并不明显，说明橡胶主簧本身的阻尼非常小，因此忽略其阻尼系数Cr，得到悬置的静刚度为Kr＝174N/mm。

4.2 上液室等效泵压面积

计算悬置等效泵压面积时需另外加一个活塞的有限元网格模型，仿真时给主簧中心位置施加一个向下的力推动液体向下挤压，液体的挤压使活塞向下移动，通过计算活塞扫过的体积与主簧的位移之比，得到悬置的等效泵压面积Ap。将橡胶主簧、加强块、液体和活塞网格导入ADINA，如图6所示，设置主簧的下表面与活塞的上表面、液体的上下表面为液固耦合面(FSI)，仿真结果如图7所示。

图7(b)中的等效泵压面积按以下公式计算：

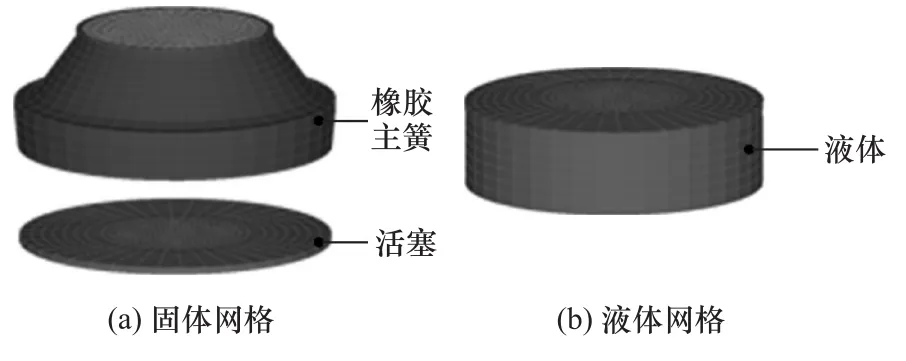
图6 等效泵压面积仿真模型

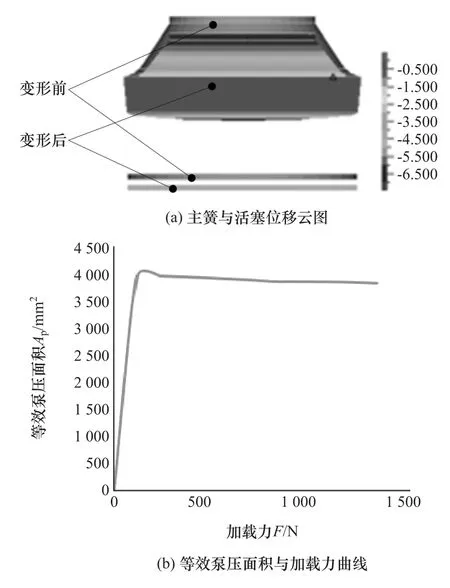
图7 等效泵压面积仿真结果

式中：Xp为活塞位移；D为活塞下端直径；Xr为主簧位移。从图7(b)中可以看到，加载力超过约100N之后，等效泵压面积基本成一条水平线，取Ap＝3847mm2。

4.3 上液室体积刚度

将橡胶主簧、加强块、解耦膜、上液室液体和空气腔气体网格导入ADINA，如图8所示。其中液体设置为不可压缩流体，气体设置为可压缩流体。

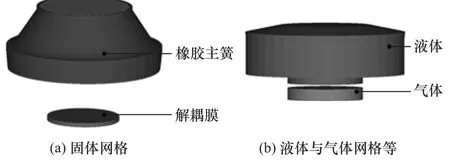
图8 上液室体积刚度仿真模型

上液室体积刚度定义为上液室压强的变化量与体积变化量之比。仿真计算时，液体入口设置在上液室液体下表面，流入液体速度为v。经过一定时间t，可得到流入上液室的液体体积和上液室的均布压强p，由此计算上液室体积刚度：

式中Sin为液体入口处的截面积。

本文中的半主动悬置具有两种工作模式：空气腔打开和关闭。仿真时，空气腔关闭定义为气体网格下表面为Wall，此时形成一个密闭的腔体。空气腔打开时取消下表面的Wall条件，此时形成一个敞开的腔体。两种模式分别计算，得到的仿真结果如图9～图12所示。

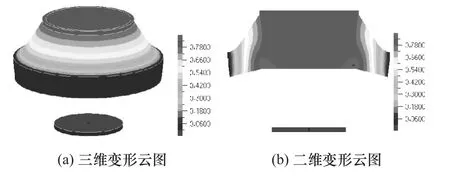
图9 硬模式固体变形云图

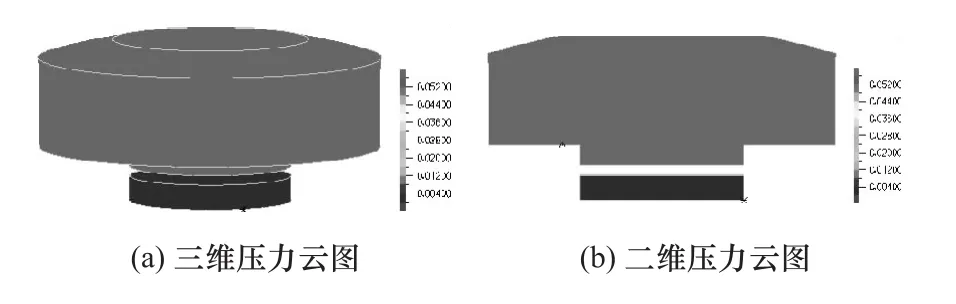
图10 硬模式流体压力云图

图11 软模式固体变形云图

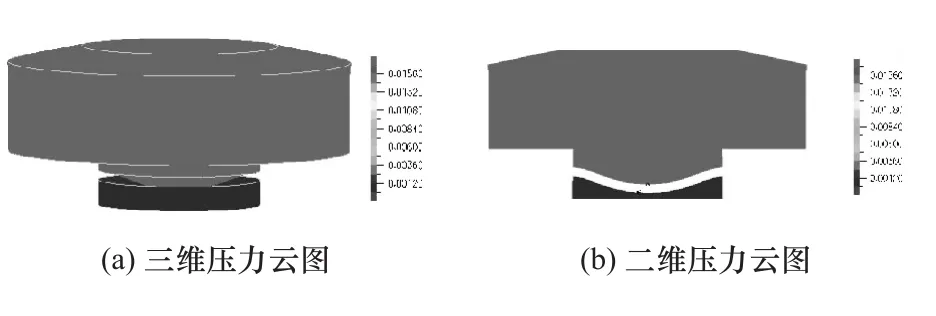
图12 软模式流体压力云图

通过提取悬置内液体的压强与流入悬置内的液体体积，得到悬置上液室的压强-体积变化曲线，如图13所示。

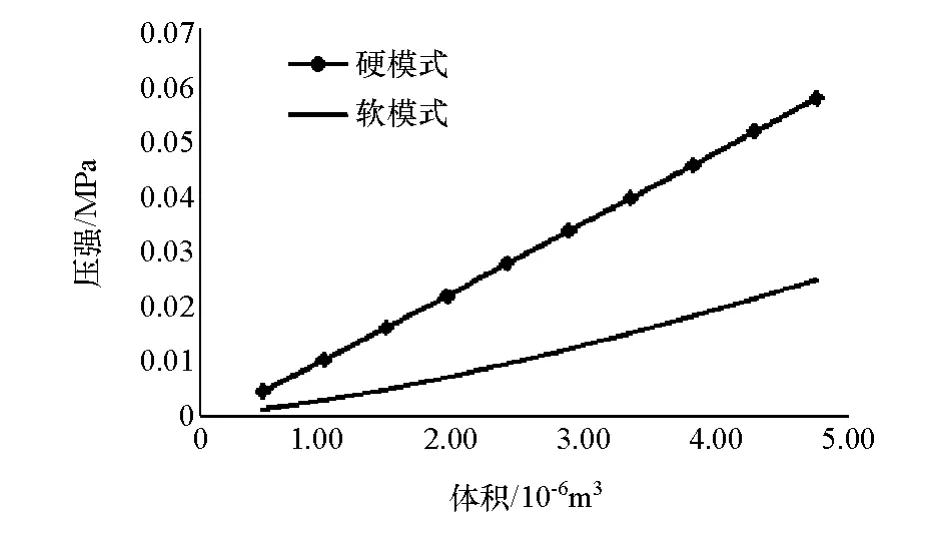
图13 软硬模式下上液室压强-体积变化曲线

根据式(11)计算得到硬模式上液室体积刚度K1off＝1.21×1010N/m5，软模式上液室体积刚度K1on＝4.94×109N/m5。

4.4 下液室体积刚度

计算下液室体积刚度只需液体与橡胶底膜的网格模型，如图14所示。仿真时，外界液体从上表面进入，进入的液体会使橡胶底膜变形。通过液体速度与时间的乘积计算流入的液体体积，同时提取下液室内压强，得到压强随液体体积变化的曲线，从而计算出下液室的体积刚度。液体入口设置在下液室液体上表面，流入液体速度为1mm/s，仿真时间为1s，结果如图15～图17所示。

图15 流体压强云图

图14 下液室体积刚度仿真模型

图17 压强-体积曲线

从图17可见，其压强-体积变化曲线近似线性，计算得到下液室体积刚度为

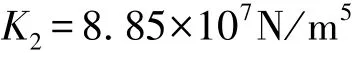
4.5 惯性通道液体惯性系数和流量阻尼系数

由式(3)可知，只要知道惯性通道两端的压强差Δp＝p1-p2，并给定惯性通道内液体的流量Q和流量的变化率Q·，便可算得惯性通道内液体的惯性系数I和流量阻尼系数R。

在时刻t，惯性通道两端的压差、流量和流量的变化率分别用Δpt，Qt和Q·t来表示，取n个时刻点，由式(3)得

对于式(12)，方程中只有两个未知数I和R，但是方程组的个数却有n个，n≫2，一般而言，该方程组无解。因此引入最小二乘法，通过最小化误差的平方和寻找方程组的最佳匹配数据，也即寻找满足所有方程组误差最小的I和R。根据最小二乘法，有

将液体和橡胶底膜网格导入ADINA中，如图18所示，在液体上表面施加随机均布压强载荷p1(频变随机压强信号)，满足低频(1～50Hz)大振幅，高频(50～200Hz)小振幅的条件，模拟了悬置的实际工作情况，p1的时域曲线与频域特性如图19所示。

加载计算后，仿真结果如图20所示。

图20 液体压强云图

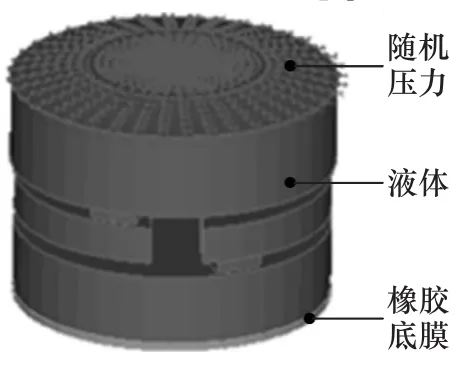
图18 惯性系数和流量阻尼系数仿真模型

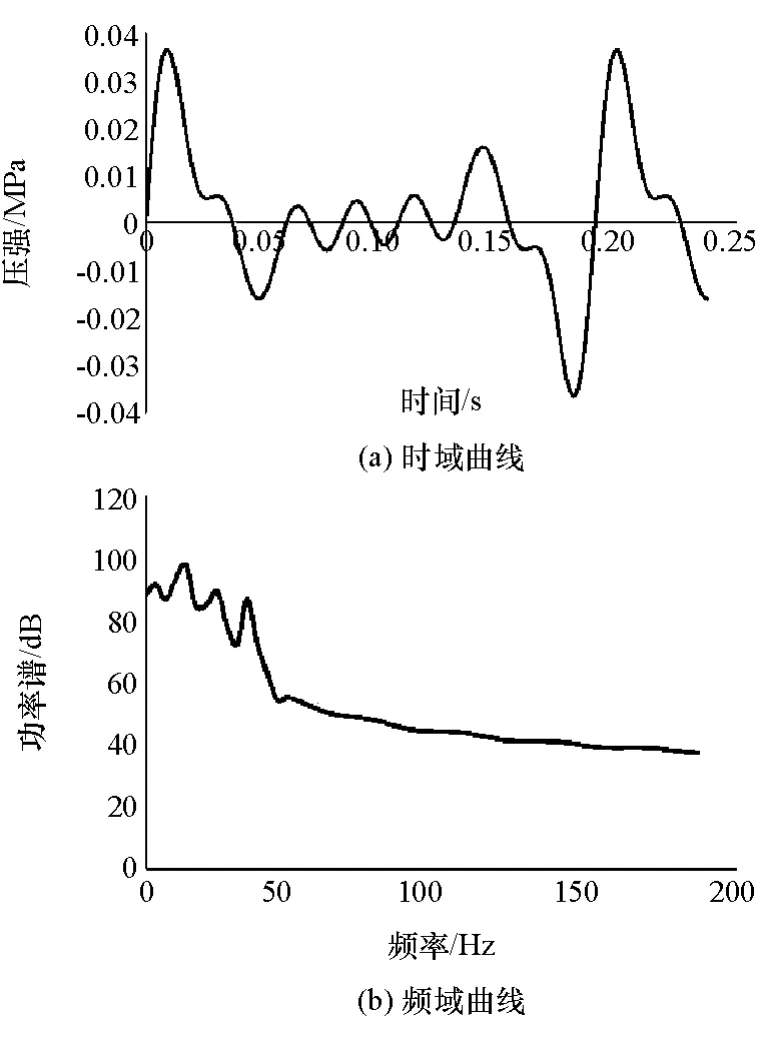
图19 输入随机压强p1

通过ADINA软件后处理，可以提取任意时刻惯性通道的出口压强p2和惯性通道内的液体流量Q，并可用Matlab求得离散数据Q的近似导数Q·，提取的压强p2和流量Q，如图21和图22所示。

将以上数据代入式(12)～式(14)，求解可得I＝1.92×106kg/m4，R＝5.5×107N·s/m5。

综上所述，通过液固气三相耦合方法辨识得到半主动悬置的建模参数如表1所示，将各个参数代入集总参数模型便可得到悬置的动态特性。

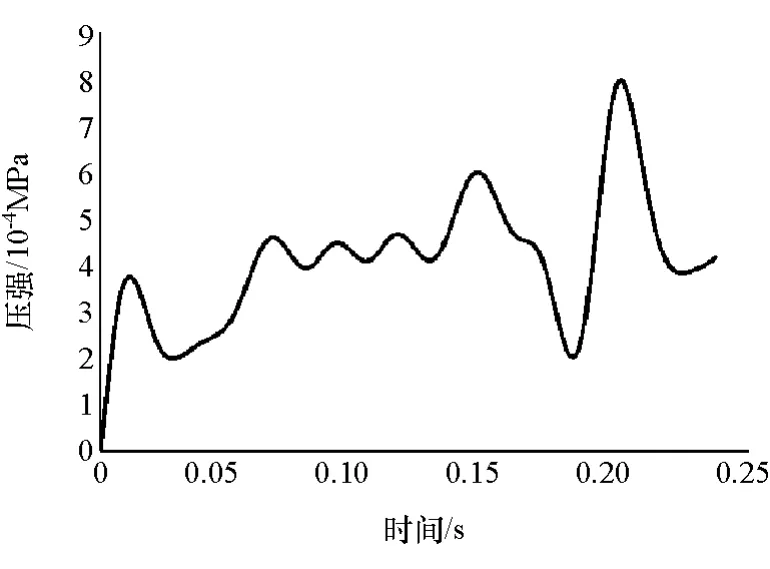
图21 惯性通道出口压强p2

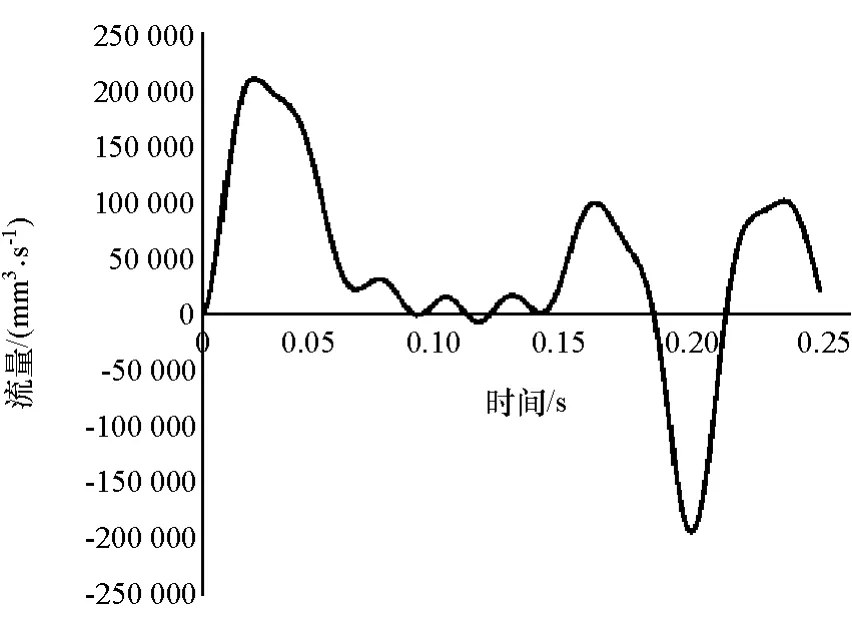
图22 惯性通道体积流量Q

表1 基于有限元的参数辨识结果

5 试验验证

通过加工制作半主动悬置样件，并在MTS831振动试验台上进行悬置的动特性试验，如图23所示。试验时，对悬置施加预载1 000N，并作用一个振幅0.5mm、振动频率范围为1～50Hz的激励。图23中电磁阀的开闭由开关控制器控制，试验得到软硬两种模式下不同的动特性曲线，如图24(a)所示。将试验曲线与通过提取仿真参数得到的动特性曲线对比如图24(b)所示。

图23 半主动悬置动特性试验

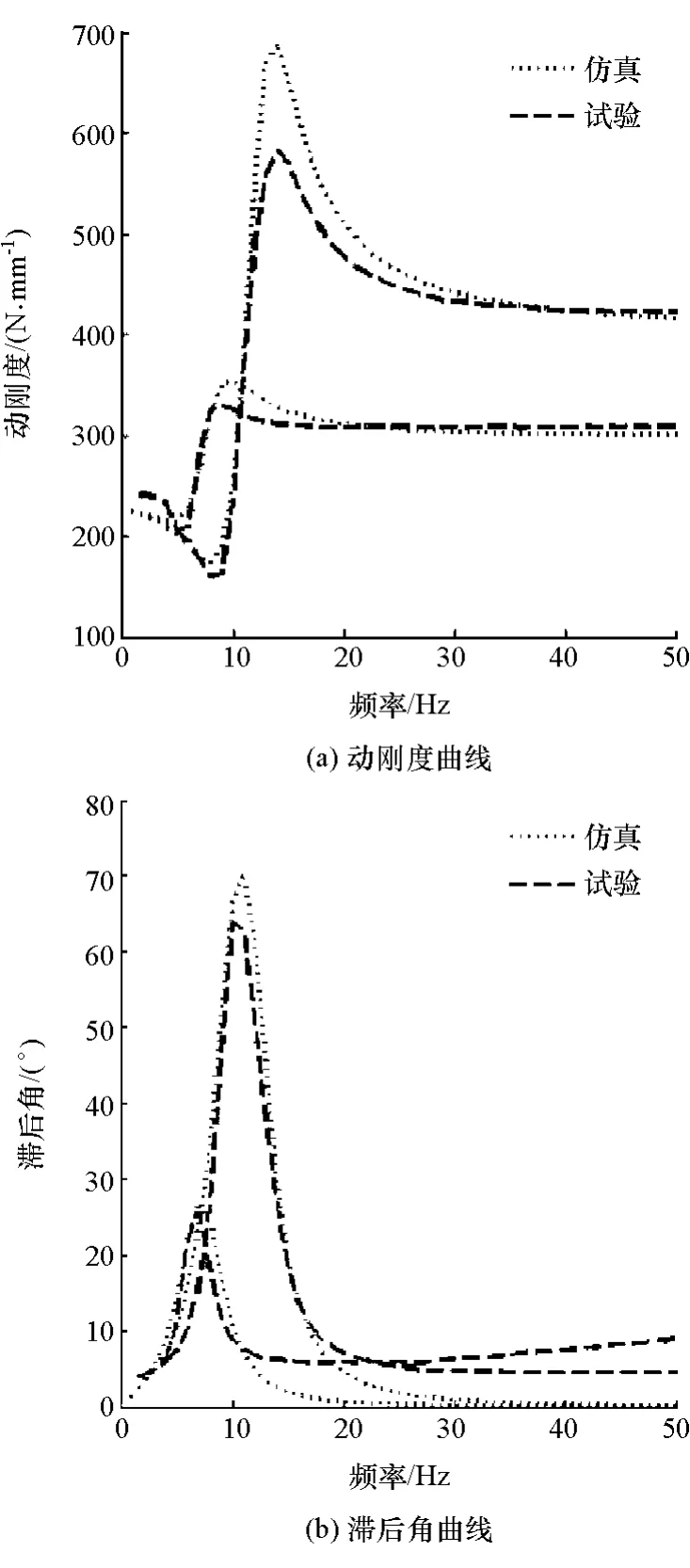
图24 半主动悬置动特性对比

由图24可见，硬模式动刚度和滞后角峰值明显大于软模式，有限元仿真结果与试验结果基本一致。有限元曲线与试验曲线中动刚度及滞后角出现的峰值频率相同，峰值大小略有差异，验证了有限元法对于半主动悬置集总参数提取的正确性，同时证明了有限元法对于半主动悬置正向开发具有较好的指导性。

对于图24中仿真曲线与试验曲线没有完全一致的原因主要有以下几点：(1)半主动悬置是一个非线性较强的系统，而本文使用的是描述半主动悬置的线性集总参数模型；(2)半主动悬置中的橡胶材料和乙二醇液体受温度影响较大，而本文中并未考虑温度的影响；(3)对于半主动悬置模型进行了一定简化，在一定程度上也影响了仿真的结果。因此，对于半主动悬置的液固气三相耦合仿真，后续拟采用更精确的模型，同时考虑温度的影响，进行悬置流固热的耦合仿真；对于半主动悬置集总参数模型，采用准确性更高的非线性模型。通过以上方法，实现半主动悬置动特性更精准的预测，为半主动悬置正向开发奠定基础。

6 结论

针对半主动悬置动特性仿真预测中，集总参数模型的关键参数难以确定的问题，采用ADINA软件，建立了解耦膜刚度控制式半主动悬置液固气三相耦合有限元分析模型，通过试验和仿真，提取了集总参数模型的关键参数，实现了对半主动悬置动特性的准确预测，主要结论如下。

(1)利用建模软件，建立了半主动悬置液固气三相耦合有限元分析模型，通过仿真计算，提取了集总参数模型的关键参数，对半主动悬置的动特性曲线进行了准确预估，很好地解决了传统识别方法的试验周期长和过程繁琐问题，为半主动悬置的结构设计和动特性分析提供了科学手段。

(2)仿真与试验动特性曲线的对比表明，液固气三相耦合有限元分析模型具有较高的预测精度，可准确提取集总参数建模的关键参数，实现半主动悬置的动特性准确预估。

后续研究拟采用模型验证技术，并考虑温度对悬置内材料的影响，提升有限元分析模型的精度，实现半主动悬置动特性的精准预测。为自主品牌汽车发动机半主动悬置的正向开发提供设计方法。

[1] FLOWCRW C.Understanding hydraulicmounts for improved vehicle noise[C].SAE Paper 850975.

[2] 李锐，陈伟民，等.基于磁流变技术的发动机隔振控制[J].机械工程学报，2009，45(3)：183-189.

[3] 邓兆学，郑玲，等.发动机磁流变半主动悬置变论域模糊控制的研究[J].汽车工程，2013，35(11)：1023-1029.

[4] 范让林，张祥龙.可变解耦膜刚度半主动液阻悬置研究[J].机械工程学报，2015，51(14)：108-114.

[5] TRUONG TQ，AHN K K.A new type of semi-active hydraulic enginemount using controllable area of inertia track[J].Journal of Sound and Vibration，2010，329：247-260.

[6] 徐志军，刘福水.半主动控制惯性通道式液力悬置开发[J].车用发动机，2008(1)：85-87.

[7] 史文库，毛阳，等.半主动液压悬置参数识别与动态特性[J].吉林大学学报(工学版)，2014，44(3)：605-611.

[8] 范让林，吕振华.液阻悬置非线性动特性及其参数识别方法[J].机械工程学报，2007，43(7)：145-151.

[9] 陆黎明，夏长高，潘道远.基于特征点法的液阻悬置集总参数模型参数识别[J].机械科学与技术，2015(10)：1580-1583.

[10] 吕振华，上官文斌.基于液—固耦合有限元仿真的液阻悬置集总参数模型动特性分析[J].机械强度，2004(1)：29-37.

[11] 王敏，姚国凤.基于流固耦合FEM的液压悬置关键参数提取[J].哈尔滨工业大学学报，2011，43(1)：158-162.

[12] 陈志勇，史文库，等.基于液固耦合有限元分析的驾驶室液压悬置结构参数[J].吉林大学学报(工学版)，2011，41(2)：99-103.

[13] 曹正林，李骏，等.考虑强液-固耦合效应的发动机液阻悬置动态特性仿真研究[J].振动与冲击，2012，31(10)：4-8.

Parameter Identification of Semi-active Engine Mount Based on Multi-field Coupling Modeling

Zheng Ling1，2，You Zuolong2，Liu Qiaobin2，Pang Jian1，3，Xu Xiaom in1，3＆Chen Daijun1，3
1.State Key Laboratory of Vehicle NVH and Safety Technology，Chongqing 401120；2.Automotive Engineering，Chongqing University，The State Key Laboratory ofMechanical Transmission，Chongqing 400044；3.Changan Auto Global R＆D Center，Changan Automobile Co.，Ltd.，Chongqing 401120

In view of the difficulty in accurately setting up multi-field couplingmodel for the optimization of semi-activemount，ADINA software is adopted to establish a liquid-solid-gas three-phase coupling simulationmodel for semi-active enginemount，and a lumped parametermodel for semi-activemount is also acquired by accurate identification and extraction of key parameters，with its dynamic characteristics studied.The results show that the ADINA-based liquid-solid-gas three-phase coupling simulation model can rapidly and accurately extract the key parameters in lumped parametermodel，realizing the accurate prediction on the dynamic characteristics of semi-active mount.The correctness ofmulti-field couplingmodeling and dynamic characteristics analysismethod are verified by tests，providing a feasible scheme for the forward developmentand structure optimization of the semi-activemount of automotive engine.

sem i-active mount；liquid-solid-gas three-phase coupling model；parameter identification；dynam ic characteristics

10.19562/j.chinasae.qcgc.2017.05.009

∗汽车噪声振动与安全技术国家重点实验室开放基金(NVHSKL-201405)资助。

原稿收到日期为2016年6月6日。

郑玲，教授，博士生导师，E-mail：zling＠cqu.edu.cn。