基于载波频率的变功率逆变器效率研究

刘向东，专祥涛

（武汉大学动力与机械学院，湖北 武汉 430072）

基于载波频率的变功率逆变器效率研究

刘向东，专祥涛

（武汉大学动力与机械学院，湖北 武汉 430072）

随着对逆变器输出性能需求的不断提高，如何在较高载波频率下进一步提升逆变器的变换效率，显得越来越重要。载波频率对逆变器的损耗有着极大的影响，不仅能影响开关损耗，同时能影响滤波电感损耗。建立逆变器的总体损耗和效率模型，以此模型为基础，在THD满足约束条件情况下，对载波频率和变功率逆变器的效率进行了优化计算和仿真，从而得到最优载波频率和最优效率。最后通过实验平台来验证仿真结果。

逆变器效率；THD约束；载波频率；最优化

新能源发电系统、不间断供电电源、电机驱动、有源电力滤波器、感应加热电源等很多重要的电力电子技术应用场合，对逆变器的性能和效率有着较高的要求。对逆变器损耗进行建模研究并且通过仿真进行优化，可以使逆变器的性能和效率达到最好，减少能源浪费。

目前，国内外对逆变器功率器件的损耗计算方法作了大量的研究。文献［1-4］根据IGBT的元件结构提出了IGBT损耗模型，但仅仅是通过元器件的物理结构和仿真软件来分析IGBT的工作电压、电流波形而得到IGBT的损耗，并没有对其进行效率优化。文献［5-8］提出了一种利用数据手册提供的器件特性参数，根据功率损耗与电压、电流等参数的函数关系估算器件损耗的方法，但是没有研究载波频率和输出功率对逆变器损耗的影响。

本文则根据器件数据资料中提供的损耗特性曲线，推导出逆变器损耗的损耗参数，不仅建立逆变器功率损耗和效率模型，而且对建立的模型在载波频率和输出功率变化的情况下进行了计算和优化，使得逆变器输出在满足谐波畸变率的限制条件下效率达到最优。

1 逆变器损耗模型

目前，逆变器损耗模型分为基于物理结构和基于数学方法2种，本文采用数学建模方法计算损耗。

1.1 导通损耗

根据逆变器运行状态可知，同一桥臂上的2个IGBT及并联二极管各负责半个周期的电流通过，则单个功率器件的通态损耗功率可以表示为［6］

式中:u为器件两端电压；iC为电流；τ(t)为占空比。式（1）可化简为

从式（2）可以看出，导通损耗的计算关键在于u和iC的关系，以及τ(t)的计算。实际上，由于u与iC是非线性关系，精确计算导通损耗就比较困难。一般将u与iC之间的关系用直线近似，则

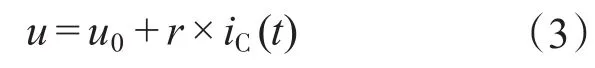
而对于占空比，双极性调制下IGBT和并联二极管是不相同的，根据运行状态可以得到两者的占空比:

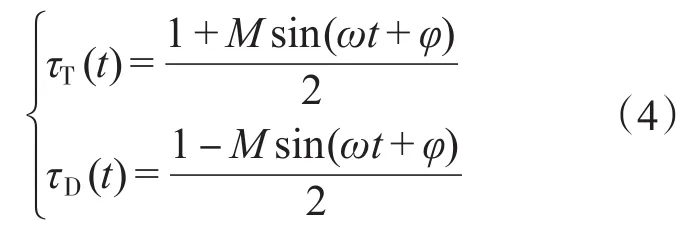
代入积分公式后计算得到IGBT和并联二极管的导通损耗功率分别为

式中:UCE0,UF0为IGBT和并联二极管门槛电压；rCE,rF为各自导通等效电阻（可通过厂家提供的电压电流曲线拟合获得）；M为调制比；φ为电压电流相位差；ICP为输出电流幅值。

1.2 开关损耗

功率器件的开关损耗与母线电压、器件型号、载波频率等因素都有关。设载波频率为fSW,则半个基波周期内单个功率器件要开通关断fSW次，故单个功率器件的开关损耗可近似表示为

一般厂家会给出在参考电压U*dc下开通一次EoniC(t)和关断1次EoffiC(t)随输出电流iC(t)的关系曲线。根据工程经验表明，可以将损耗与电流的关系线性化，通过计算后得到IGBT和并联二极管的开关损耗功率为（由于二极管开通损耗很小，可忽略不计）

式中:Udc为直流母线电压为额定工作电流；为额定工作电压为额定电压和额定电流I*C下IGBT开通一次损耗能量；Eoff_P为额定电压U*dc和额定电流I*C下IGBT关断1次损耗能量；Err_P为额定电压U*dc和额定电流I*C下二极管关断1次损耗能量。

一般IGBT模型包括了IGBT和并联二极管，则逆变器开关元件的总损耗可以表示为

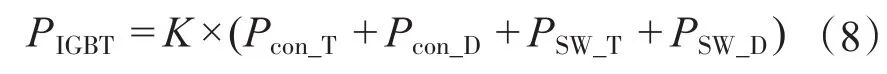
式中:K为开关管个数。

1.3 滤波电感损耗

滤波电感损耗分为铜损耗和铁损耗。铜损在忽略掉集肤效应情况下，主要来自于电感的内阻消耗，即Pcu=I2R，电流近似为输出电流，电阻R为电感内阻。而铁损(PFe)主要为磁芯损耗，磁性材料在交变磁场中，会产生功率损耗:磁滞损耗(Ph)、涡流损耗(Pe)和剩余损耗(Pc)，这3种损耗都通过热量消耗出去。这3种损耗的计算公式都相对独立，为了方便计算，目前工程上应用比较广泛的方式是Steinmetz方程，它将三者损耗合并为1个公式。首先计算出磁芯损耗的功率密度，然后根据磁芯重量大小，算出磁芯的总体损耗。磁损的功率密度Pv（单位W/cm3）表示为

式中:Cm,α,β为系数（由磁芯厂商给出，或者根据铁损曲线拟合得到）；Bm为磁感应强度的峰值。

1.4 损耗分析

为方便逆变器能效分析，本节对以上损耗模型进行分析，可以得到逆变器元件损耗随输出功率和载波频率的变化曲线分布图，有助于分析器件功率损耗对逆变器效率的影响变化。图1为载波频率固定在10 kHz和30 kHz情况下，开关元件、滤波电感铜损铁损和总损耗随着输出电流（输出功率）的变化曲线。曲线表明:电感的铁损基本没有变化，开关器件损耗和电感铜损会随着输出电流的增加而增加。图2为输出电流固定在10 A和30 A情况下，开关元件、滤波电感铜损铁损和总损耗随着载波频率的变化曲线。曲线表明:电感的铜损基本没有变化，电感铁损会随着载波频率的增加而减少，开关器件损耗成线性增加，总损耗则先减少后增加。

图1 定频下损耗随功率变化曲线Fig.1 The loss curve varies with power under the constant frequency

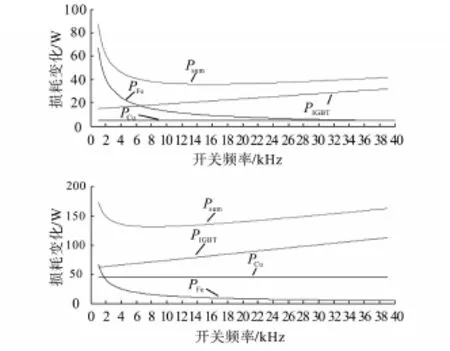
图2 定功率下损耗随频率变化曲线Fig.2 The loss curve varies with frequency under the constant power

2 逆变器效率优化模型

2.1 优化模型建立

由上述逆变器损耗模型，可以得到逆变器能源转换效率为

其中，η是关于载波频率fSW的函数，因此，可以通过调节载波频率使逆变器损耗达到最小，即效率达到最优。则优化变量设为载波频率，对应的优化目标为

式中:Urms为输出电压有效值；Irms为输出电流有效值；PIGBT为开关器件损耗。

2.2 约束条件

约束条件如下:

1）由于载波频率不仅会影响逆变器的效率，同时还会影响输出总谐波畸变量，即输出波形质量。因此，在对效率进行优化时必须保证输出波形质量满足要求。

对逆变器输出进行谐波分析可以得到双极性SPWM调制下谐波模型为

其中

式中:L,C分别为滤波电感值和电容值；N为半周期载波数，与fSW相关为整数。为基本频率。

设定THD约束条件，即

2）功率器件对载波频率还有上、下限，即

因此，上述优化模型转化如下:

式中:C为整数。

2.3 优化算法

上述优化模型是1个含非线性约束条件的非线性优化问题，为方便问题求解，首先对模型进行简化:

1）对逆变器输出总谐波畸变量模型分析可以得出，谐波含量THD与载波频率fSW是单调关系，载波频率越大，THD反而越小；

2）由效率模型可知，输出功率一定时，逆变器损耗最小即代表效率最高。

根据以上2点，式（17）含THD约束条件的优化问题最终可以转化为

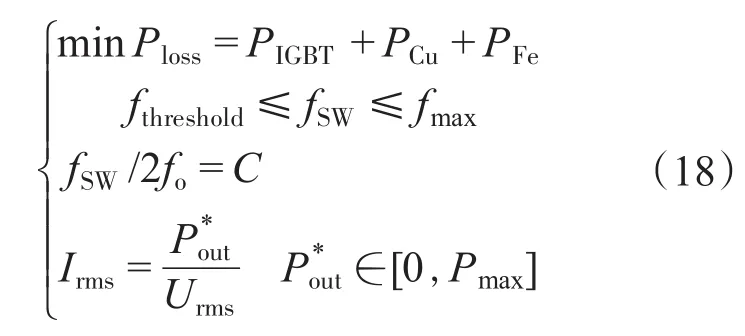
式中:fthreshold为THD=THDconstraint对应的载波频率；C为整数。

令:

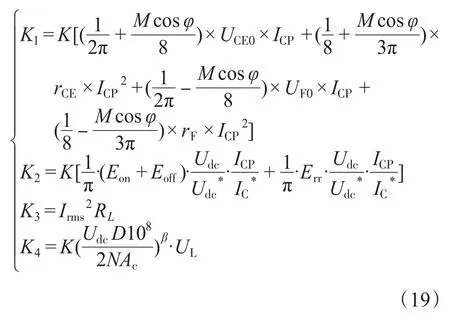
则优化目标变为

式（20）是含1个变量的经典优化求极值问题，求导分析后可知目标有最小值，对应最优载波频率为

由以上分析可知，优化模型求解基本完成，但还有关键一点:fthershold值的求解。由于单调关系，可以根据要求采用多种算法来求解fthershold,本文采用二分法。最终，最优载波频率可以表示为

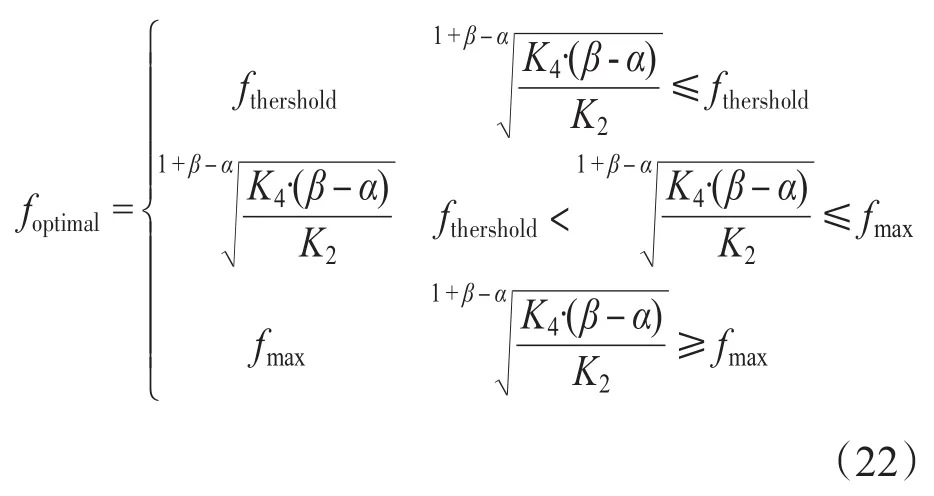
上述优化求解整体步骤流程如图3所示。

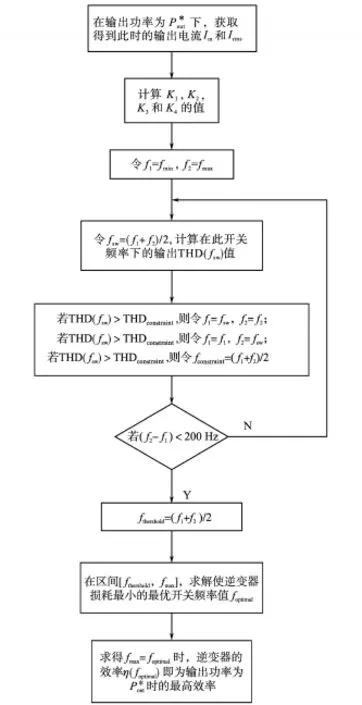
图3 优化求解流程图Fig.3 The flow chart of optimization calculation

3 算例分析

3.1 参数设置

选用英飞凌IKW20N60T作为开关元件，根据其Datasheet所提供的元件参数和元件输出特性曲线图和开关损耗曲线图可以得到元件的损耗参数，具体如下:IGBT门槛电压UCE0=0.9 V，IGBT通态等效电阻rCE=0.028 Ω，IGBT开通损耗Eon=0.31e-3 J，IGBT关断损耗Eoff=0.46e-3 J，二极管门槛电压UF0=1.1 V，二极管通态等效电阻rF= 0.024 Ω，二极管关断损耗Err包含在IGBT开关损耗中。

逆变器运行参数设置如下:直流母线电压362 V，输出电压220 V，输出工频频率50 Hz，滤波电感3.45 mH，滤波电容6.85 μF，输出THD约束1%。

3.2 变功率优化效果分析

根据上述建立的逆变器效率优化模型，以及给定的系统参数，使逆变器在最优载波频率模式下运行，并对优化结果进行分析。图4、图5给出了逆变器最优效率及对应的最优频率、THD随输出电流的变化曲线图。

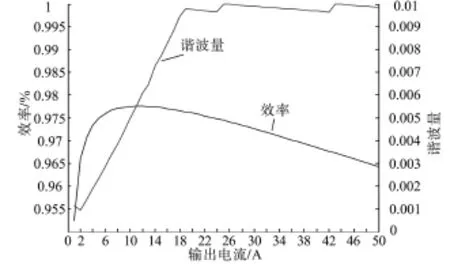
图4 最优效率和THD随输出电流变化曲线Fig.4 The optimal efficiency and the THD curves with the output current

图5 最优效率和载波频率随输出电流变化曲线Fig.5 The optimal efficiency and frequency curves with the output current

从图5中曲线可以看出，逆变器最优载波频率会随输出电流的增大而成递减趋势，而图5中载波频率一直要维持在10 kHz以上，原因在于THD的约束条件。

图6给出了在10 kHz载波频率附近，不同功率下的THD随载波频率变化图。可以看出，在载波频率小于10.5 kHz左右时，THD会超过1%。此外，在载波频率固定下，输出功率越大，THD值越小；输出功率固定下，载波频率越大，THD值越小。

图6 不同功率下THD随频率变化曲线Fig.6 The curves of THD varies with frequency under the different power

3.3 对比分段变频控制

为验证采用最优载波频率控制对逆变器效率的提升效果，本文在此采用简单的分段频率控制法来对比。这里选用20 kHz，25 kHz，30 kHz作为控制频率，分别计算出3种固定频率下，效率随着输出功率的变化曲线，如图7所示。

图7 3种频率控制效率对比曲线Fig.7 The contrast curves of efficiency under three frequency control

图8 最优效率曲线和分段变频效率对比曲线Fig.8 The efficiency comparison curves between optimal and sectional variation of control frequency

选取每个输出功率下最大效率的频率作为控制频率，如0～3A内30 kHz载波频率的效率最大，在这段区间选择30 kHz作为控制频率。以此类推确定所有功率下的3种控制频率所对应的最大效率曲线［9］。将分段变频控制效率曲线与最优效率曲线作对比，如图8所示。根据曲线对比结果可以得到，采用最优载波频率控制能够有效地提升逆变器的效率。

4 实验验证

实验平台以DSP为基础，对自制逆变器进行变频、输出反馈控制。使用功率分析仪PA1000测量输入端的功率，使用单片机进行输出功率的采集测量，并且用万用表测量值作为参考校正。

经过试验，我们得到理论计算和实际检测数据。表1为理论计算效率与实际测量效率在3种不同输出功率下的对比表，由表1可以看出，建立的模型在不同频率下理论计算效率与实际的逆变器测量效率差别不大，基本相似。

表1 理论计算效率与实际测量效率对比Tab.1 The comparison of theoretical efficiency and practical efficiency

图9 定频控制和最优频率控制效果对比曲线Fig.9 The comparison curves of effect under the constant frequency and optimal frequency control

同时，在低输出功率下进行优化结果验证。图9为逆变器实验平台在最优控制频率和10 kHz频率下的实际损耗和效率对比图，在逆变器运行15 s左右加大输出功率，运行到31 s左右降低输出功率。由于测量仪数值会在小范围内变动，因此损耗曲线会有波动，但是可以看出理论计算的最优频率控制效果明显优于定频10 kHz。进一步验证了理论优化计算的可行性。

5 结论

本文建立了逆变器损耗和效率模型，在THD满足要求的情况下，通过理论计算对模型进行最优化，使得逆变器随输出功率、载波频率变化的效率最优，从而得到最优载波控制频率。通过实验验证，该模型可以类比实际逆变器的损耗，并且逆变器使用最优控制频率比其他控制频率下效率有显著提升，应用在实际情况中能够使得逆变器延长逆寿命且节约能源。

［1］Shen Z John，Xiong Yali，Cheng Xu，et al.Power MOSFET Switching Loss Analysis:a New Insight［J］.Industry Applications Conference，2006，3（2）:1438-1442．

［2］Mantooth HA，Hefner AR.Electro-thermal Simulation of an IGBT PWM Inverter［J］.IEEE Transactions on Power Electronics，1997，12（3）:474-484.

［3］Githiari A N，Gordon B M，McMahon Richard A，et al.A Comparison of IGBT Models for Use in Circuit Design［J］.IEEE Transactions on Power Electronics，1999，14（4）:607-614.

［4］张明元，沈建清，李卫超，等.一种快速IGBT损耗计算方法［J］.船电技术，2009，29（1）:33-36.

［5］Frede Blaabjerg，Ulrik Jaeger，Stig Munk-Nielsen.Power Losses in PWM-VSI Inverter Using NPT or PT IGBT Devices［J］.IEEE Transactions on Power Electronics，1995，l0（3）: 358-367.

［6］Casanellas F.Losses in PWM Inverters Using IGBTs［J］. IEEE Proceedings-electric Power Applications，1994，141（5）: 235-239.

［7］Dittmann N，Schulz A，Loddenkotter M.Power Integration with New Econo-PIM IGBT Modules［C］//Industry Applications Conference，1998，2:1091-1096.

［8］谢勤岚，陈红.PWM逆变器中IGBT的损耗计算［J］.中南民族大学学报（自然科学版），2003，22（1）:39-41.

［9］Li Yong，Zheng Jerry.A Low-cost Adaptive Multi-mode Digital Control Solution Maximizing AC/DC Power Supply Efficiency［C］//Applied Power Electronics Conference and Exposition（APEC），2010:349-354.

Research on Inverter′s Efficiency with Variable Power Output Based on Carrier Frequency

LIU Xiangdong，ZHUAN Xiangtao
（School of Power and Mechanical Engineering，Wuhan University，Wuhan 430072，Hubei，China）

With the demand of the inverter performance and power density increasing，it becomes more and more important how to improve the switching efficiency of inverter in high carrier frequency.The carrier frequency has a great impact on the loss of the inverter，including the switching loss and the filter inductance loss.The loss model and efficiency model of an inverter were established as the bench.With this model，the carrier frequency and the efficiency of a variable power inverter were optimized and simulated with the constraints on THD satisfied，and the optimal carrier frequency and optimal efficiency were obtained.Finally，the mathematical results are verified on an experimental platform.

inverter efficiency；THD constraint；carrier frequency；optimization

TM464

A

10.19457/j.1001-2095.20170506

2016-03-28

修改稿日期：2016-09-01

刘向东（1991-），男，硕士研究生，Email:1310247658@qq.com