基于激光跟踪仪的新型顺次多边法

张振久，刘明俊，赵振宇，王均伟

(1. 深圳信息职业技术学院机电工程学院，广东 深圳 518172；2. 深圳市雷赛控制技术有限公司，广东 深圳 518055)

基于激光跟踪仪的新型顺次多边法

张振久1，刘明俊1，赵振宇1，王均伟2

(1. 深圳信息职业技术学院机电工程学院，广东 深圳 518172；2. 深圳市雷赛控制技术有限公司，广东 深圳 518055)

针对空间3D坐标检测问题，提出一种基于激光跟踪仪的新型顺次多边法。此方法的测量系统包括一台激光跟踪仪和四个附加靶座，其中四个附加靶座的相对位置已经通过顺次多边法进行了校正。把一台激光跟踪仪依次安装在三个不同的位置，并利用激光跟踪仪检测附加靶座及被测点与各个激光跟踪仪站位之间的距离。执行四次多边法，就能够得到被测点的空间坐标。利用实验验证了顺次多边法的有效性，x、y和z的最大测量误差分别为2.65μm、2.43μm和2.68μm。

3D坐标检测 多边法 顺次多边法 激光跟踪仪

激光跟踪仪是一种基于球坐标系统的大尺度测量系统，在大尺寸工件装配、反求工程、大型自由曲面精度评定以及机床误差检测等方面都有激光跟踪仪的用武之地[1-3]。但是，相对于其出色的测长功能，其测角精度低很多，导致其空间坐标的测量精度并不高，因此，单站激光跟踪仪不适合高精度空间坐标检测的应用场合。

多边法能够实现高精度空间坐标检测[4-6]。多边法仅利用跟踪仪的干涉测长功能，而不使用低精度的测角功能，大大提高了空间坐标的测量精度。研究人员对于多边法的系统布局进行了深入分析，给出多边法的最佳布局[5,7-9]。在最佳布局情况下，多边法的空间坐标测量精度优于1μm，此精度足以满足诸如自由曲面精度评定和机床误差补偿方面的应用要求，甚至可以用于校准CMM[10-11]。相对于传统的基于激光干涉仪的CMM和机床误差检测方法，基于多边法的误差检测方法无需对准工作，操作简单，对操作人员的技术水平要求不高，是一种更加高效的方法。

多边法需要使用至少四台激光跟踪仪，其成本比较高。因此有研究人员提出了顺次多边法[12]，此方法使用一台激光跟踪仪顺次在四个位置对目标点进行检测。由于仅使用了一台激光跟踪仪主，测量系统的成本大大降低。但是此方法的检测精度较低，因为被测量点的重复性会给系统自标定引入误差。

本文提出一种新型的顺次多边法。在文献[12]中的顺次多边法中引入了四个附加靶座，用以减少被测点重复性引入的测量误差。由于本方法也仅使用一台激光跟踪仪，所以其成本与顺次多边法相当，远低于传统多边法。本文介绍了此方法的基本原理，并建立了测量系统的数学模型。用仿真和实验验证了新型多边法的有效性。

1 新型顺次多边法

1.1 新型顺次多边法

此测量系统由一台激光跟踪仪和四个附加靶座O、Q、K和P0组成，如图1示。四个附加靶座的位置可以通过传统多边法进行标定，这会在下一节进行论述。

按照下面的方法建立坐标系：O点设为坐标系原点，Q点位于X轴上，X-Y平面通过点K，Z轴垂直于X-Y平面且通过原点O。因此，O、Q和K的坐标分别为(0, 0, 0)、(xQ, 0, 0)和(xK, yK, 0)。由于激光跟踪仪测量长度增量的精度远高于检测绝对长度的精度，因此，定义点P0(x0, y0, z0)为参考点，将会为下方所述的测量方法提供绝对参考长度。

把激光跟踪仪固定于某个位置Sj(xSj, ySj, zSj)。用激光跟踪仪检测参考点P0与激光跟踪仪位置Sj之间的绝对参考长度lj，然后分别检测点O、Q、K和被测点Pi(xi, yi, zi)与激光跟踪仪之间的长度增量（相对于RAD）ΔlOj、ΔlQj和ΔlKj以及Δlij。

首先，利用多边法，建立方程组

求解公式（1）中的方程组即可获得Sj点坐标(xSj, ySj, zSj)和绝对参考长度lj。

然后利用Δlij，可以建立一个方程

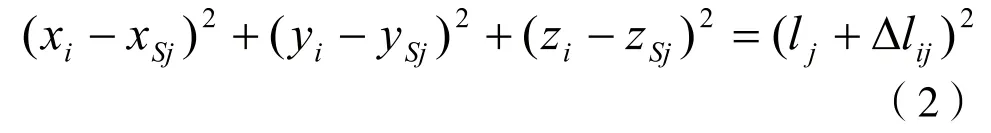
分别使激光跟踪仪位于S1、S2和S3，重复上述过程三次，就可以得到三个方程(2)组成方程组(3)，解之即可获得被测点Pi的坐标(xi, yi, zi)。

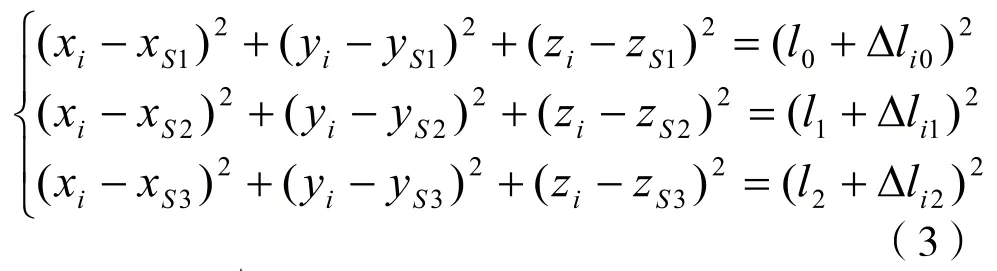
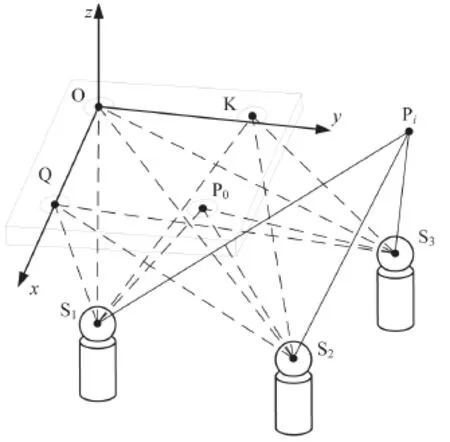
图1 新型顺次多边法原理Fig.1 The principle of the novel sequential multilateration method

1.2 附加靶座的标定

四个附加靶座的坐标需要提前标定，才能实用于顺次多边法测量系统。本文利用文献[12]中的顺次多边法，使用一台激光跟踪仪实现四个附加靶座的标定。不同于文献[12]中的顺次多边法，本文预标定附加靶座的过程中，所有10个靶座都是固定不动的，因此标定过程中目标点的重复性对自标定的影响非常小。

如图2示。包括四个附加靶座在内，总共有10个点被用来进行标定操作。将激光跟踪仪分别固定于Sj，j=0, 1, 2, 3共4个位置上，利用传统多边法中的方法建立坐标系，并设P0为参考点。当激光跟踪仪固定于某个站位时Sj，均可以检测得到各个被测点与激光跟踪仪之间的距离，并利用两点间距离公式，获得10个方程。因此，四站激光跟踪仪检测之后，可以建立总共包含40个方程的方程组。求解此方程组，即可获得各个点的坐标。其中的四个附加靶座的坐标就此确定。

图2 四个附加靶座的标定Fig.2 Calibration of the four additional target caves

1.3 仿真分析

激光跟踪仪的测长精度对顺序多边法的精度影响非常大。利用文献[10]中的方法对本文所使用的FARO跟踪仪进行精度测试，即利用一台最大允许误差为(0.9+L/333)μm的CMM和激光跟踪仪进行比较。实验中，对距离激光跟踪仪约1m左右的8个点进行测试。此8点组成一个直径为300mm的圆且每个点与激光跟踪仪的距离大约相等。测量过程中，将某任意参考点到跟踪仪之间的距离设置为参考绝对长度，其它点与第一个点之间的长度增量由激光跟踪仪测量得到。而各个点的相对坐标由CMM测得。利用多边法自校正技术，可以求出激光跟踪仪和各个点之间的绝对距离以及跟踪仪的基点坐标。重复20次实验，最终得到激光跟踪仪测量长度增量的最大偏差和重复性为0.807μm和0.334μm。

接下来，利用计算机仿真技术，对本文所提出的新型顺次多边法进行模拟。测量系统包含四个中继靶座和三个激光跟踪仪，其中激光跟踪仪顺次安装于三个不同的站位，也就是说测量系统总共占据七个空间位置。七个点可以建立一个立方体。因此，典型的测量系统布局应该是：四个中继靶座和四个跟踪仪站位分别位于一个立方体的角点上，且此立方体包含整个测量空间，如图3所示。P0、O、Q、K点代表中继靶座，S0、S1、S2代表跟踪仪站位。

根据3σ准则，令激光跟踪仪检测长度增量的误差符合正态分布N (0, 0.269μm)，仿真计算空间内各点的坐标检测精度，仿真计算次数为10000次。

图3 新型顺次多边法的布局Fig.3 Arrangement of the novel sequential multilateration method

2 空间坐标检测实验

如图4示, 为验证本文所提出的顺次多边法的有效性，利用一台最大允许定位误差为(0.9+L/333) μm的参考CMM进行对比实验，实验中，反射器随着CMM测量头运动，运动空间大小为300mm×300mm×300mm的网格，相邻两点之间的距离为150mm，因此共有27个被测量点。因为CMM是参考标准，因此实验中认为CMM的定位误差为零，并认为测量误差均是由顺次多边法所引起的。测量结果如图5示。

由实验结果可以看出，x、y和z的最大偏差分别为2.65μm、2.43μm和2.68μm；每个点的测量重复10次并对测量结果取均值，x、y和z的测量误差都分别小于0.76μm、0.75μm和0.81μm；以10次检测结果的方差来定义重复性，各个点的x、y和z的测量重复性均小于0.74μm、0.78μm和0.86μm。

图4 实验装置Fig.4 The experimental setup

表1 仿真结果Tab.1 Simulation results

图5 顺次多边法的实验结果Fig.5 The experimental results of sequential multilateration method.

3 结论

本文提出一种新型的基于激光跟踪仪的顺次多边法，能够精确地检测空间坐标。把四个附加靶座引入到测量系统中来提高系统自标定的精度。利用CMM作为参考，对此顺次多边法进行了实验验证，x、y和z的最大测量偏差分别为2.65μm、2.43μm和2.68μm。并且，如果对10次测量的结果取均值，能够大大提高测量精度。

由于本方法仅使用了一台激光跟踪仪，其成本大大低于传统多边法。同时，仿真计算证明了本文所提出的方法的性能能够满足诸如机床几何误差检测、工件加工质量检验和自由曲面点云检测等方面的精度要求。

[1] 张振久, 胡泓, 刘欣. 基于激光跟踪仪的机床导轨系统误差检测[J]. 中国激光, 2011, 38(9): 0908002. ZHANG Zhenjiu, HU Hong, LIU Xin. Meas urement of geometric error of machine tool guideway system based on laser tracker[J]. Chinese Journal of Lasers, 2011, 38(9): 0908002. (in Chinese)

[2] LIU Wanli, OUYANG Jianfei, QU Xinghua, YAN Yonggang. Misalignment error calibration of faro retro probe for laser tracker system[J]. Chinese Optics Letters, 2007, 5(5): 281-282. (in Chinese)

[3] 李杰, 伍凡, 吴时彬, 匡龙, 林常青. 使用激光跟踪仪测量研磨阶段离轴非球面面形[J]. 光学学报, 2012, 32(1): 0112002. LI Jie, WU Fan, WU Shibin, KUANG L ong and L IN Changqing. Using a laser tracker to measure the surface of off-axis aspheric mirror during grinding[J]. Acta Optica Sinica, 2012, 32(1): 0112002. (in Chinese)

[4] Takatsuji T, Goto M, Kurosawa T, Tanimura Y and Koseki Y. The first measurement of a three-dimensional coordinate by use of a las er tracking interferometer system based on trilateration[J]. Measurement Science and Technology, 1998, 9(1), 38-41.

[5] Takatsuji T, Goto M, Kirita A, Kuros awa T and Tanimura Y. The relationship between the m easurement error and the arrangement of laser trackers in laser trilateration[J]. Measurement Science and Technology, 2000, 49(5):477-483.

[6] ZHANG Zhenjiu, HU Hong. A general strategy for geometric error identification of multi-axis machine tools based on point measurement[J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(5): 1483-1497.

[7] ZHANG Guoxiong, LI Xinghua, LIN Yongbing, et al.. A Study on the Optimal design of laser-based multi-lateration systems[J]. CIRP Annals. 2003, 52(1):427-430.

[8] ZHANG Defen, ROLT Stephen, MAROPOULOS Paul G. Modelling and optimization of novel laser multilateration schemes for high-precision applications[J]. Measurement Science and Technology, 2005, 16(12): 2541-2547.

[9] 林永兵, 张国雄, 李真, 李杏华. 四路激光跟踪三维坐标测量系统最佳布局[J]. 中国激光. 200 2, 29(11): 1000-1005. LIN Yongbing, ZHANG Guoxiong, LI Zhen, LI Xinghua. Optimal arrangement of four-beam laser tracking system for 3D coordinate measurement[J]. Chinese Journal of Lasers, 2002, 29(11): 1000-1005.(in Chinese)

[10] LIN Chienchang, HER Juiliang. Calibrating the volumetric errors of a precision machine by a laser tracker system[J]. The International Journal of Advanced Manufactur ing Technology, 2005, 26(11): 1255-1267.

[11] JIANG Hong, OSAWA Sonko, TAKATSUJI Toshiyuki, NOGUCHI Hironori, KUROSAWA Tomizo. Highperformance laser tracker using an articulating mirror for the calibration of coordinate measuring machine[J]. Optical Engineering, 2002, 41(3): 632-637.

[12] Schwenke H, Schmitt R, Jatzkowski P and Warmann C. On-the-fly calibration of linear and rotary axes of machine tools and CMMs using a tracking interferometer[J]. CIRP Annals, 2009, 58(1):477-480.

[13] WANG Jindong, GUO Junjie, ZHANG Guoxiong, GUO Baoan, WANG Hongjian. The technical method of geometric error measurement for multi-axis NC machine tool by laser tracker[J]. Measurement Science an d Technology, 2012, 23(4):45003-45013.

Novel Sequential Multilateration Method Based on Laser Tracker

ZHANG Zhenjiu1, LIU Mingjun1, ZHAO Zhenyu1, WANG junwei2
（1. School of Mechanical and Electrical Engineering, Shenzhen Institute of Information Technology, Shenzhen 518172, P.R. China；2. Shenzhen Leadshine Control Technology Co. Ltd, Shenzhen 518055, P.R. China）

A novel sequential multilateration method for measuring the three dimensional (3D) coordinates based on a laser tracker is presented. The measuring system consists of a laser tracker and four additional target caves of which the relative positions have been pre-calibrated by sequential multilateration principle. The laser tracker is located at three different stations sequentially, and the 3D coordinates of the laser tracker's stations can be determined by the four additional target caves based on multilateration principle. And then, the 3D coordinates of the under-test points can be determined by the three las er tracker's stations based on trilateration method. The validity of the propos ed method is demonstrated by conducting an actual measurement experiment, and the measurement errors of x, y and z are found to be less than 2.65μm, 2.43μm and 2.68μm respectively.

3D coordinates measurement; multilateration principle; multi-station and time-sharing measuri ng method; computer simulation;laser tracker

TN247

：A

：1672-6332（2017）01-0015-05

【责任编辑：高潮】

2017-03-02

深圳市科技计划(GRCK20160415111859786，JCYJ20160415114050831)

张振久(1982-)，男(汉)，黑龙江人，博士，讲师，主要研究方向：精密加工与检测，计算机视觉和数字图像处理。E-mail：zhangzhenjiu@sziit.edu.cn