微纳卫星L1点Halo轨道转移轨道设计

高永飞，王兆魁

（1.国防科学技术大学 航天科学与工程学院，长沙 410073；2.清华大学 航天航空学院，北京 100084）

微纳卫星L1点Halo轨道转移轨道设计

高永飞1，王兆魁2

（1.国防科学技术大学 航天科学与工程学院，长沙 410073；2.清华大学 航天航空学院，北京 100084）

针对地月空间探测任务的高风险、高成本，提出了利用微纳卫星完成地月空间环境监测、未知空间探索及地月空间动力学验证的方案，从而为未来建立地月空间运输系统建立良好基础。借助地月空间三体动力学和小推力轨道设计中的直接法，设计了针对微纳卫星的低能耗地月转移方案。结果表明：微纳卫星借助火箭上面级，从GEO轨道出发飞向L1点Halo轨道，所需速度增量为1.033 km/s，转移时间为40.02 d；不借助火箭上面级，所需速度增量为1.397 5 km/s，转移时间为48.7 d。

微纳卫星；地月转移；低能耗

0 引 言

地月空间探测已逐渐成为人类重要的航天活动。我国自正式开展月球探测工程以来，也已圆满完成了从“嫦娥1号”到“嫦娥3号”的月球探测任务，为人类和平利用地月空间迈出了新的一步。地月空间建立太阳能电站、空间站、无线电通讯中继站，或者作为太空探索多元化目的地的通道，为人类发展提供了能源、高位置资源和军事战略资源。因此，为充分利用地月空间或进一步走向深空，建立地月空间运输系统是十分必要的。

地月空间运输系统基于近地停泊轨道、地月转移轨道、地月驻留轨道和近月停泊轨道建立。近地停泊轨道可以选用低地球轨道（Low Earth Orbit，LEO）、同步转移轨道（Ceostationary Transfer Orbit，GTO）或地球同步轨道（Geosynchronous Orbit，GEO）[1]。位于LEO的国际空间站可为地月空间运输系统提供在轨服务；GTO、GEO则具有较高的能量，可为建立可重复使用运输系统降低能量代价；地月转移轨道可以分为两大类：脉冲转移轨道和小推力转移轨道。脉冲转移轨道适合于载人深空探测或其他快速响应任务，小推力转移轨道由于转移时间长、载荷比高则更适合于货运飞船或其他对于转移时间没有严格要求的任务。Halo轨道由于能够连续观测太空环境，且由其衍生得到的不变流形可以作为低能耗转移通道，可以选作地月空间驻留轨道；近月停泊轨道则是月球探测的中转站。同时，地月空间运输系统的建立还需要对地月空间辐射环境或其他环境参数进行有效监测，以提高系统安全性；对地月空间动力学进行验证，为运输系统建立奠定基础。然而，探测地月空间未知环境或执行高风险任务，高成本、高风险极大地限制了人类航天活动。

微纳卫星因其低成本在近地空间科学探测任务中得到了广泛应用。由于使用了商业货架组件以及标准机械/电子接口，微纳卫星可以通过搭载不同的科学探测载荷完成不同的科学任务，如地球观测、生物研究等[2-3]。随着航天技术和微电子技术的飞速发展，将微纳卫星应用于月球或小行星探测已逐渐成为可能[4]。“行星际探路者”（INSPIRE）是JPL（Jet Propulsion Laboratory，喷气推进实验室）规划的利用微纳卫星探测深空的首个任务，任务包括两颗3U微纳卫星，均搭载磁强计和相机；其主要任务是飞离地球150万 km，以验证微纳卫星在深空中的生存能力[5]。其他3项微纳卫星深空探测任务计划搭载NASA的空间发射系统（Space Launch System，SLS）于2018年发射[6]。

本文以微纳卫星地月空间探测为背景，以地月空间探测的技术验证、未知环境探测等高风险任务为主要目标，设计符合微纳卫星约束和任务目标的地月转移轨道。轨道设计中，借助三体动力学和小推力轨道设计，以尽可能降低转移能耗。

1 轨道设计方法

1.1 不变流形

本文基于圆形限制性三体模型：两主天体分别为地球和月球，且共同绕地月质心旋转。圆形限制性三体模型的动力学方程可表示为

其中：X为航天器状态量

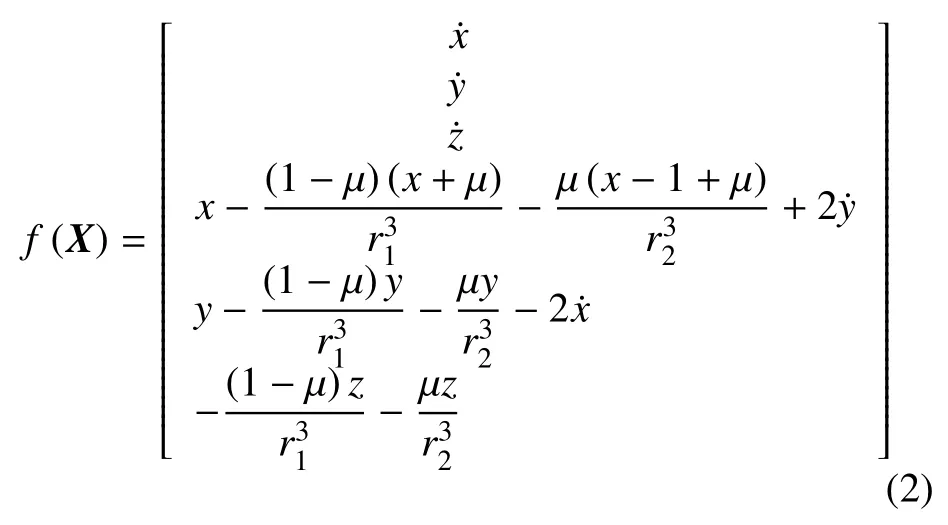
两主天体地球和月球的质量分别为m1和m2，有

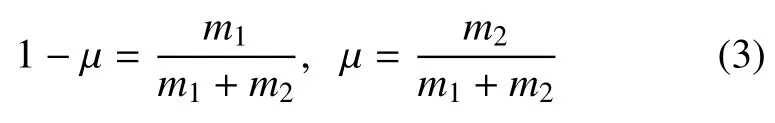
其中：在地月圆形限制性三体模型中，µ≈0.012。r1和r2分别为航天器至两主天体的无量纲距离

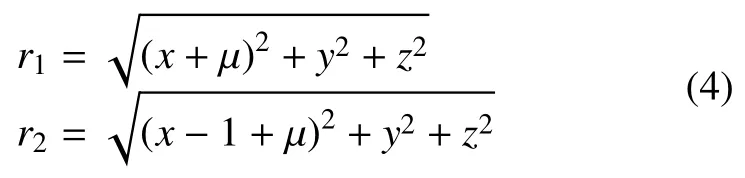
圆形限制性三体模型中存在5个平动点，且在平动点周围存在周期轨道。基于三阶Halo轨道解析解和微分校正方法[7]，图1给出了一条L1点附近的Halo轨道。

图1 L1点附近的Halo轨道Fig.1 Halo orbit around L1

由Halo轨道衍生的不变流形可用于低能耗地月转移轨道设计。下面给出不变流形的计算方法。不变流形计算涉及到周期轨道的Monodromy矩阵。记Monodromy矩阵为M，则

其中：Φ为状态转移矩阵；T为轨道周期。状态转移矩阵可通过求解变分方程得到。

其中：A(X)=df(X)/dX。

记Monodromy矩阵的稳定特征值和不稳定特征值对应的特征向量分别为，将其单位化可得

从而稳定流形和不稳定流形的初始状态可以定义为

其中：Xperiod是周期轨道上的任意一点；d是沿稳定特征向量或不稳定特征向量方向一个小的扰动。正负号则表示了扰动可以沿两个相反的方向。图2给出了图1所示Halo轨道的不变流形在O-XY平面的投影。

图2 L1点Halo轨道的不变流形Fig.2 Invariant manifold of Halo orbit around L1

1.2 小推力轨道设计

基于圆形限制性三体模型，当考虑小推力时，航天器动力学方程可以写为

其中：r和v分别为航天器的位置和速度状态量；m是航天器质量；Tmax是发动机最大推力幅值；Isp为发动机比冲；g0是海平面重力加速度。控制量包括节流系数u∈[0,1]和推力方向α。g(r)和h(v)分别为

初始状态约束和终端状态约束可表示为

小推力轨道设计通常可以转化为最优控制问题，即在动力学方程和边界条件的约束下，寻找最优控制率使得目标函数取极值。通常情况下，目标函数取转移时间、转移能耗和转移能量。本文中，目标函数取转移时间最优，即

求解最优控制问题式(9)～(12)的方法主要包括3类：直接法、间接法和混合法[8-13]。本文采用直接法求解。直接法的主要思想是将状态量和控制量离散化，从而将动力学方程约束借助插值算法转化为等式约束，结合边界约束条件，利用非线性优化工具包求解得到最优控制律和航天器状态量。

本文采用3次插值多项式对动力学方程离散化，借助matlab非线性优化工具fmincon，利用序列二次规划（Sequentral Quadratic Programming，SQP）非线性优化算法求解得到小推力轨道[14]。

2 地月转移轨道设计

微纳卫星一般作为火箭的第二载荷发射入轨，其初始轨道由火箭主任务决定。因此微纳卫星入轨的初始速度和能量会随着主任务的不同而有所不同。LEO、GTO、GEO或其他高能量轨道都可能成为微纳卫星的初始入轨轨道。

微纳卫星由于结构大小的限制，只能配置具有高比冲的微小型等离子推进系统，故微纳卫星在入轨后，只能依靠自身的连续小推力推进系统完成各项任务。表1给出了用于微纳卫星轨道设计的各项参数[15]。

表1 微纳卫星参数Table 1 Parameters of nanosat

考虑微纳卫星搭载LEO或GEO轨道任务的运载火箭，其入轨初始轨道可以为LEO、GTO或GEO轨道。但微纳卫星若从LEO轨道出发飞至地球静止轨道高度，转移时间约为100 d左右，其主要寿命阶段停留在近地空间。表2给出了微纳卫星的初始入轨状态。

表2 微纳卫星初始入轨状态（地球旋转坐标系，无量纲）Table 2 Initial state of nanosat（rendezrous coordinate system, non-dimensional）

图3给出了微纳卫星由GTO轨道出发的小推力轨道（O-XY平面投影）。从GTO轨道出发至地球静止轨道高度，近地转移时间约为40 d左右。

图3 GTO轨道出发的小推力轨道Fig.3 Low thrust orbit from GTO

进一步，考虑运载火箭于GEO轨道将微纳卫星释放，或者火箭上面级于GEO轨道继续为其提供推力，从而为微纳卫星提供更大的初始速度。为了验证地月空间动力学或尽可能降低对微纳卫星推进系统的要求，借助不变流形进行轨道设计是十分必要的。图4给出了小推力轨道和L1点Halo轨道的稳定流形。通过遍历选取截面上稳定流形的交点，并分别将交点状态作为小推力轨道设计的终端约束条件，优化得到从GEO出发飞至Halo轨道的低能耗转移轨道。

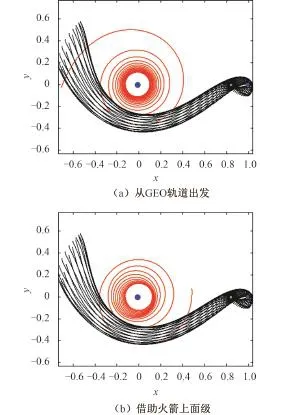
图4 小推力轨道和L1点Halo轨道稳定流形Fig.4 Low thrust orbit and invarint manifold from Halo orbit around L1

图5给出了从GEO出发飞至Halo轨道的低能耗转移轨道。微纳卫星经过一段时间的小推力飞行，进入稳定流形，进而沿着稳定流形进入Halo轨道。整个飞行过程所需的速度增量为1.397 5 km/s，转移时间为48.7 d。

图5 GEO轨道出发飞向Halo轨道Fig.5 Set off from GEO to Halo orbit

图6中，微纳卫星由火箭上面级释放。火箭上面级可为微纳卫星提供约150 m/s的速度冲量。整个转移过程类似图5，所需速度冲量为1.033 km/s，转移时间是40.02 d。

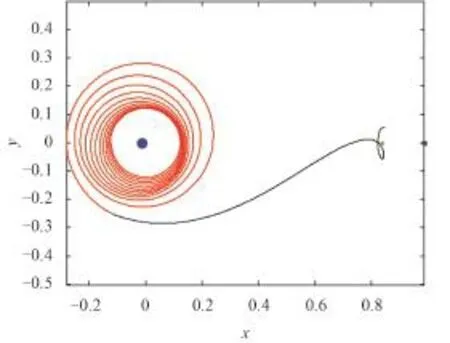
图6 由火箭上面级释放Fig.6 Released by upper stage of the rocket

3 结 论

本文提出了利用微纳卫星执行地月空间环境监测、未知环境探索及地月空间动力学验证等高风险、高成本探测任务，从而为建立地月空间运输系统奠定良好基础。

本文结合地月三体动力学和小推力轨道设计方法，设计了微纳卫星从GEO飞向L1点Halo轨道的低能耗转移轨道，并设定利用火箭上面级助推将微纳卫星送入低能耗转移轨道。

[1]Folta D，Dichmann D，Clark P，et.Al.Lunar cube transfer trajectory options[C]//AAS/AIAA Space Flight Mechanics Meeting：25th.[S.l.]：AIAA，2015.

[2]Kitts C，Hines J.Initial flight results from the pharmasat biological microsatellite mission[C]//AIAA，23rd Annual Conference on Small Satellites.[S.l.]：AIAA，2009.

[3]Kane V.Planetary cubesats begin to come of age[EB/OL].(2015-02-17)[2016-11-25].http://www.planetary.org/blogs/guest-blogs/van-kane/ 20150217-planetary-cubesats-begin-to-come-of-age.html.

[4]Klesh A，Baker J，Castillo-Rogez J，et.al.Inspire：interplanetary nanospacecraft pathfinder in relevant environment[C]//AIAA SPACE 2013 Conference and Exposition.[S.l.]：AIAA，2013.

[5]Wall M.Tiny Cubesats set to explore deep space[EB/OL].[2016-11-25].http://www.space.com/29306-cubesats-deep-space-exploration.html.

[6]刘林，侯锡云.深空探测轨道理论与应用[M].北京：电子工业出版社，2015.

[7]Zhang C，Zhao Y.Low-thrust minimum-fuel optimization in the circular restricted three-body problem[J].Journal of Guidance，Control，and Dynamics，2015，38(8)：1-9.

[8]Ozimek M T，Howell K C.Low-thrust transfers in the earth-moonsystem，including applications to libration point orbits[J].Journal of Guidance，Control，and Dynamics，2010，33(2)：533-549.

[9]Senent J，Ocampo C.Low-thrust variable-specific-impulse transfers and guidance to unstable periodic orbits[J].Journal of Guidance，Control，and Dynamics，2012，28(2)：280-290.

[10]Sukhanov AA，Prado A F B D A.Optimization of transfers under constraints on the thrust direction：Ⅰ[J].Cosmic Research，2008，45(1)：417-423.

[11]Mingotti G.Optimal low-thrust invariant manifold trajectories via attainable set[J].Journal of Guidance，Control，and Dynamics，2011，34(6)：1644-1656.

[12]Sukhanov A A，Prado A F B D A.Optimization of transfers under constraints on the thrust direction：Ⅱ[J].Cosmic Research，2007， 45(5)：417-423.

[13]袁建平，赵育善，唐歌实.航天器深空飞行轨道设计[M].北京：中国宇航出版社，2014.

[14]Conversano R W，Wirz R E.CubeSat lunar mission using a miniature ion thruster[C]//47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exihibit，[S.l.]：AIAA，2011.

高永飞（1989– ），男，博士研究生。主要研究方向：地月空间轨道动力学。

通信地址：清华大学航天航空学院（100084）

电话：（010）62794316

E-mail：gaoyongfei_001@hotmail.com

Transfer Orbit Design for L1 Halo Orbit Based Nanosats

GAO Yongfei1，WANG Zhaokui2
（1.Institute of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China；2.School of Aerospace，Tsinghua University，Beijing 100084，China）

Nanosats have been demonstrated the capability of deep space exploration with the availability of onboard control systems, such as propulsion, active attitude control, navigation as well as communication, thermal or other subsystems design required for deep space.Nanosats are usually launched as second ary payloads into different orbits.In this paper, aiming at lunar exploration with nanosats, the concepts that nanosats transfer to the moon from the deployments in geosynchronous transfer orbit(GTO) or released by the upper stage were put forward and the heteroclinic connection between L1 and L2 Lyapunov orbit was designed.In the orbit design, both the dynamical system approach and the low thrust model were used to realize low energy cost orbit transfer in order to satisfy the limited condition of propulsion subsystems.

nanosat；cis-lunar transfer；low cost

V412

：A

：2095-7777（2017）01-0072-05

10.15982/j.issn.2095-7777.2017.01.011

高永飞，王兆魁.微纳卫星L1点Halo轨道转移轨道设计[J].深空探测学报，2017，4（1）：72-76.

Reference format：Gao Y F，Wang Z K.Transfer orbit design for L1 Halo orbit based nanosats [J].Journal of Deep Space Exploration，2017，4（1）：72-76.

[责任编辑：高莎，英文审校：朱鲁青]

2016-11-25

2016-12-20

国家自然科学基金资助项目（1157020588）