电力系统连锁故障多阶段动态博弈防御模型

刘军，王健，廖叔洋，李洋

（1.国网安徽省电力公司淮南供电公司，安徽淮南232001；2.国网安徽省电力公司滁州供电公司，安徽滁州239000；3.国网安徽省电力公司检修公司，安徽合肥230061；4.国网安徽省电力公司亳州供电公司，安徽亳州236800）

电力系统连锁故障多阶段动态博弈防御模型

刘军1，王健2，廖叔洋3，李洋4

（1.国网安徽省电力公司淮南供电公司，安徽淮南232001；2.国网安徽省电力公司滁州供电公司，安徽滁州239000；3.国网安徽省电力公司检修公司，安徽合肥230061；4.国网安徽省电力公司亳州供电公司，安徽亳州236800）

近年来，国内外发生了多起连锁故障引起的大停电事故，阻止连锁故障发展、避免大停电事故发生对保障电力系统安全稳定运行具有重要的现实意义。为了防御由连锁故障引发的大停电事故，提出一种考虑参与人有限理性的连锁故障多阶段动态博弈防御模型。基于故障方的有限理性假设和故障方行动的关联性假设，综合考虑元件自身故障、外界环境、潮流转移和隐性故障等因素对元件停运概率的影响，提出基于实时运行条件的元件停运概率表征有限理性的故障方不完美的选择能力；根据可掌握的事故状态信息，提出潮流转移严重度和系统失负荷严重度表征故障方追求自身利益的意识；并进一步基于风险分析方法，生成故障方的策略集合。从风险理论的角度出发，将运行风险作为收益函数，用于定量评估防御方行动的有效性。最后，以IEEE39节点系统为例，验证了该模型的合理性。

连锁故障；有限理性；多阶段动态博弈；策略集合；收益函数；电力系统

0 引言

近年来，国内外电力系统发生多起连锁故障导致的大停电事故，造成了巨大的经济损失和灾难性后果［1-2］。大停电事故的调查报告指出，安全分析技术的缺乏和实时状态感知能力的不足是导致调度部门不能阻止单一元件故障引起连锁反应的两个主要原因［3］。迄今为止，研究人员在连锁故障防御控制的研究领域做了很多工作。文献［4］从预防线路连锁跳闸角度提出了一种大电网在线分布式计算的多智能体控制方法，通过优化切机切负荷控制策略来预防连锁故障的发生。文献［5］提出一种基于线路相关集的后备保护控制策略，可以实现后备保护与安全自动装置的协调配合，防止大停电事故的发生。文献［6］借鉴多智能体系统理论，提出了基于离线断面功率传输极限分析的广域协同预控制系统，防止区域内故障因调度控制失误引发连锁故障。

博弈论是以参与人之间有针对性的行为产生的互动过程为研究对象的理论。连锁故障的发展过程中扰动与控制交替进行，相互影响，共同作用于电网，具有互动性和对抗性，这使得博弈论适用于连锁故障防御的研究。文献［7］基于完全信息静态博弈防御模型，研究预防针对性攻击的最优防御方案。文献［8］基于不完全信息静态博弈防御模型，研究预防针对性攻击的最优防御方案。上述博弈防御模型都是建立在假设故障方具有完全理性的基础上，即认为故障方总是能够有效识别并采取对电网影响最大的扰动，而实际上连锁故障的发展过程包含了大量的不确定性因素，忽略这些因素会导致故障方生成的策略集合遗漏后果相对较小但风险较大的故障，不能涵盖当前运行工况下防御方最需要关注的潜在危险扰动；此外，博弈过程的收益函数只考虑了系统的停电损失，未考虑控制措施产生的代价，因此不能准确评估控制措施的有效性。

在上述背景下，提出故障方的有限理性假设和故障方行动的关联性假设，建立一种考虑参与人有限理性的连锁故障多阶段动态博弈防御模型。通过风险分析方法，生成故障方的策略集合，并从风险理论的角度出发，将运行风险作为收益函数。最后，通过算例分析计算验证了模型对连锁故障防御的有效性。

1 多阶段动态博弈与连锁故障博弈

多阶段动态博弈是指博弈过程分为多个阶段，且参与人的行动有先后顺序的博弈，其博弈过程常用博弈树的形式来表示。博弈树由节点和枝组成，其中节点可分为决策节点和末端节点。决策节点i表示参与人i的行动起点，末端节点是博弈结束的地方，末端节点k唯一对应着一个策略组合sk和一个收益组合uk。决策节点i下的枝j表示参与人i的可选策略sij，所有的枝即构成参与人i的策略集合Si；每一条枝都是从一个决策节点出发，并唯一的指向另一个决策节点或末端节点。具有二阶段的连锁故障博弈防御过程的博弈树如图1所示。

图1 具有二阶段的博弈树

当电网发生连锁故障时，扰动与控制交替进行，如果将电网发生的扰动假设为一个“虚拟人”的行动，系统调度人员会针对其行动采取相应的控制措施，并且双方都力图选择对自己最为有利或最为合理的方案，那么连锁故障的防御过程可表示为故障方和防御方的多阶段动态博弈。多阶段动态博弈包括参与人、策略集合和收益函数，在连锁故障的多阶段动态博弈防御中：

1）参与人：包括故障方和防御方，将电网扰动定义为故障方，将调度部门定义为防御方。

2）策略集合：故障方的策略集合包括不同类型的扰动，防御方的策略集合包括调度部门采取的控制措施。

3）收益函数：故障方的收益为造成的控制代价风险和停电风险，防御方的收益为付出的控制代价风险和停电风险，其中故障方的收益非负，防御方的收益非正，两者收益之和为零。

为了便于分析连锁故障在多个阶段中的博弈过程，用D表示一条路径中故障方或防御方的决策节点的个数，即博弈过程的阶段总数，用d表示故障方和防御方处于第d个阶段。则连锁故障多阶段动态博弈防御的数学模型可表示为

式中：I=（1，2）分别表示故障方和防御方；Sdi表示参与人i在第d个阶段的策略集合；Ui是参与人i的收益函数。

结合电网中的实际情况，做如下假设：

1）故障方的有限理性假设。参与人的理性体现在两个方面，一是参与人决策行为的目标，二是参与人追求目标的能力；完全理性的参与人不仅以个人利益最大化为目标，而且具有准确的判断选择能力，也不会“犯错误”［9］。在连锁故障发展过程中，由于大量不确定因素的影响，电网扰动虽然总会给系统造成负面影响，但每次发生的扰动却不一定是当前运行状况下后果最严重的那一个。即故障方虽然以自身利益最大化为目标，但它并没有完美的选择能力，其选择的策略可能不能满足其追求最大利益的目标，因此故障方只具有有限理性。

2）防御方的完全理性假设。假设防御方具有完全理性，即其总能针对故障方的行动制定出最好的策略。

2 考虑参与人有限理性的连锁故障多阶段动态博弈防御模型

2.1 有限理性故障方的行动预测

2.1.1 故障方行动的概率预测

1）故障方初始行动的概率。当故障方在初始阶段采取行动时，即d=1时，故障方初始行动的概率主要受线路自身故障因素和外界环境因素的影响，取pw表示线路自身故障因素和外界环境因素引起线路停运的概率。

线路自身故障因素主要考虑线路老化失效，线路单位长度老化失效故障率记为λo；外界环境因素主要考虑天气变化引起的线路偶然失效，线路单位长度偶然失效故障率记为λw［10］。综合考虑线路自身故障因素和外界环境因素，线路单位长度故障率λ可表示为

在相同的时间内，线路的停运概率与线路的长度和单位长度故障率成正比［10］，将所有线路长度与单位长度故障率乘积的归一化数值作为线路停运概率，则故障方在初始阶段采取第m个行动的概率为p11m

式中：λm为线路m的单位长度故障率；Lenm为线路m的长度；L为系统所有线路的集合。

2）故障方后续行动的概率。当故障方在后续阶段采取行动时，即d∈［2，D］时，故障方在第d个阶段行动的概率会受到故障方在第d-1个阶段行动的影响，包括潮流转移和其他不明原因的因素的影响。

当线路m严重过载时，即线路m的潮流超过其极限值，故障方在后续阶段采取第m个行动的概率为1，即

当无线路严重过载时，故障方在后续阶段行动的概率主要考虑潮流转移和其他不明因素的影响。

定义线路停运概率pzy，当线路潮流F在正常水平时，线路停运概率主要受线路自身随机故障因素的影响，此时pzy=pw；当线路潮流在正常水平上限值与极限值Fmax之间时，假设pzy随F的增大而线性增大［11］。潮流转移引起的故障方在后续阶段采取第m个行动的概率为

式中：Fm为线路m当前的潮流值；Fnormalmax，m为线路m的潮流正常值上限；Fmax，m为线路m的潮流极限值。

其他不明原因的因素引起的故障方在后续阶段采取第m个行动的概率记为。

综合以上因素，故障方在后续阶段采取第m个行动的概率pd1m为

2.1.2 故障方行动的后果预测

防御方能够获得故障发生后的事故状态信息，然而大量信息的涌入往往导致调度人员无所适从或判断错误［12］，因此如何筛选出有效信息，并从这些信息中了解故障发生对电网造成的影响程度，是防御方采取行动的重要前提。为此分别定义潮流转移严重度指标和系统失负荷严重度指标。

式中：Fm，0为线路m故障前承担的有功功率；Fn为线路n在线路m故障后承担的有功功率；Fn，0为线路n在线路m故障前承担的有功功率；Fm，max为线路m潮流极限值；Fn，max为线路n潮流极限值。

式中：PS为系统总负荷量；PLj为线路m故障后母线j的失负荷量；N为系统所有母线的集合。

式中：omg1、omg2为权重因子，表示各指标在后果指标中的重要程度，可采用层次分析法求取。

2.1.3 故障方的策略集合

为了充分体现故障方在不确定性条件下追求最大收益的意识和不完美的选择能力，定义风险系数为

为了减少博弈树的规模，故障方可通过设定阀值，选择出风险系数较大的故障方行动形成故障方的策略集合。

2.2 完全理性防御方的防御策略

在缓慢相继开断阶段，连锁故障的发展过程主要以线路过载的形式呈现［13］。据此提出针对潮流过载的过负荷控制。

根据直流潮流方程，节点k对线路m的灵敏度ηmk为

式中：ΔPk为节点k的注入功率变化量；i和j分别为线路m的首节点和末节点；ΔFij为线路m的潮流变化量；Δθi、Δθj分别为线路m两端节点的相角；xij为线路m的电抗；eik和ejk分别为节点电纳矩阵的逆矩阵中的元素。

在求取灵敏度矩阵后，可根据各功率注入节点灵敏度的大小来选择最佳控制节点对［14］，求取功率调整量。

2.3 博弈过程的风险收益函数

使用失负荷量来衡量停电损失和控制代价。其中，控制代价为防御方的过负荷控制导致的失负荷量。停电损失主要包括3种类型：线路的连续开断导致所有向某个或某几个负荷供电的线路全部断开；系统解列后，为保持2个电气岛有功分别平衡而加入控制措施后导致的失负荷量；系统失稳后，为了使系统恢复稳定而加入稳定控制措施后导致的失负荷量［15］。

由于停电损失和控制代价只有在故障方行动后才会产生，其造成的影响受到行动概率的影响，因此本文从风险的角度出发，分别定义停电风险、控制代价的风险和运行风险，将运行风险作为博弈过程的收益函数。针对策略组合sk对应的路径，其停电风险、控制代价的风险和运行风险分别为

进一步，可得到故障方和防御方在该路径下的收益函数为

2.4 博弈过程的结束条件

博弈过程中故障方和防御方交替行动，只要故障方采取行动，防御方就要做出相应的调整，因此只有故障方才能结束博弈。考虑两种结束条件：当故障方的行动次数到达预先设定的深度时；当故障方的行动造成系统暂态失稳。

2.5 连锁故障多阶段动态博弈防御流程

综上所述，考虑参与人有限理性的连锁故障多阶段动态博弈防御流程为：

1）设定博弈过程的阶段总数D，将故障方和防御方所处阶段数d初始化为1；

2）预测故障方的行动，计算故障方采取各行动的概率和故障方行动的后果，并进一步计算故障方采取各行动的风险系数，生成故障方的策略集合；

3）故障方在策略集合中选择风险系数最大的策略并采取行动，判断系统是否功角失稳，若失稳，则进入步骤6）；若稳定，则进入步骤4）；

4）判断是否有线路过载，若有线路过载，则防御方采取行动，消除线路过载，并进入步骤5）；若没有线路过载，则直接进入步骤5）；

5）判断故障方所处的阶段是否达到阶段总数D，若未达到，则d=d+1，并返回步骤2）；若达到，则满足博弈过程的结束条件，进入步骤6）；

6）计算出故障方和防御方的收益函数u1和u2；

7）多阶段动态博弈防御过程结束。

连锁故障多阶段动态博弈防御流程如图2所示。

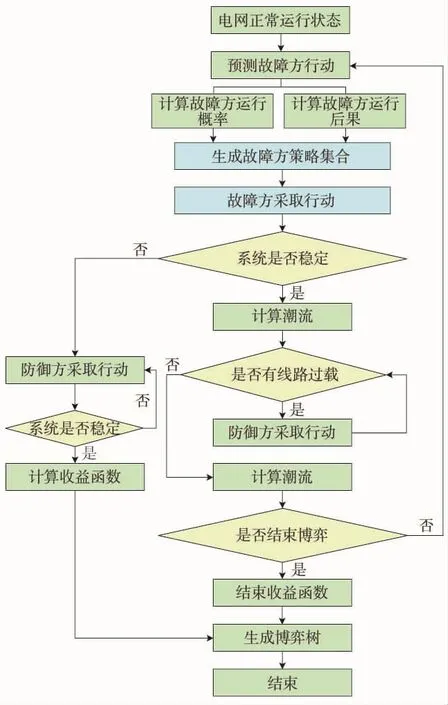
图2 连锁故障多阶段动态博弈防御流程

3 算例

仿真计算以IEEE39节点系统为例。其中各线路的潮流正常值的下限Fnmoirnmal都取0，线路m的潮流正常值的上限Fnmoarxmal取线路m的潮流额定值，线路m的潮流极限值Fmax取线路m潮流额定值的1.4倍，其他不明原因的因素引起的故障方在后续阶段行动的概率记为取0.000 2。

3.1 故障方在初始阶段的策略集合

计算故障方在初始阶段行动的风险系数，按设定的阀值进行筛选，得到故障方在初始阶段的策略集合如表1所示。

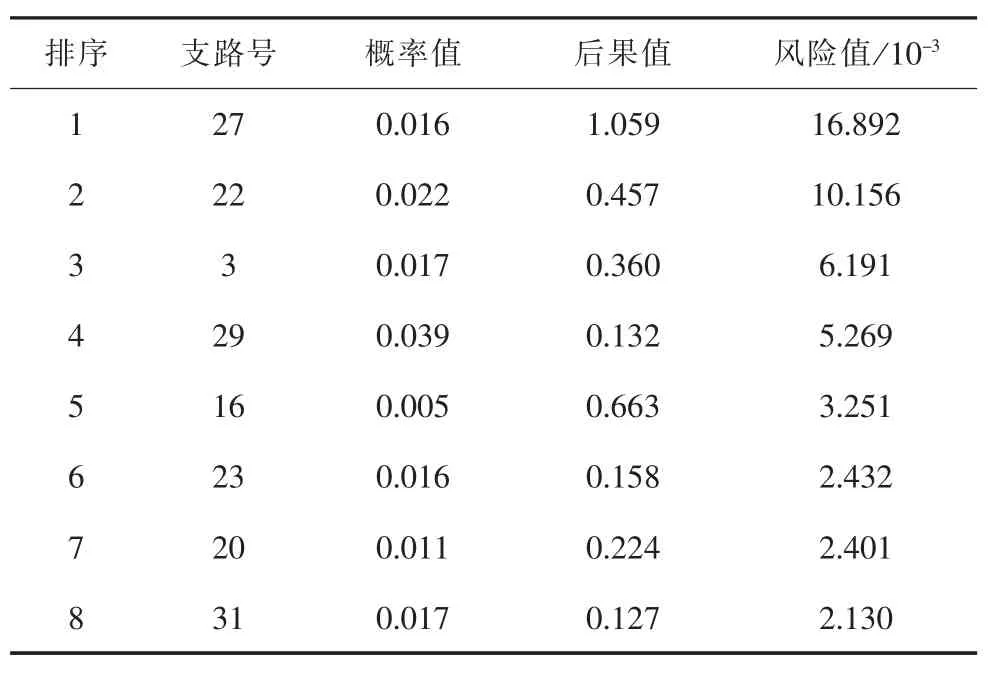
表1 故障方初始策略集合

3.2 连锁故障的多阶段动态博弈防御

选取风险系数最大的线路27故障并退出运行作为故障方在初始阶段的行动，分析连锁故障的多阶段动态博弈防御过程。

线路27开断后连锁故障的演化过程如表2所示。

表2 线路27开断后的连锁故障演化过程

针对表2的连锁故障演化过程，根据图3中多阶段动态博弈防御流程，生成每个阶段针对故障方行动的防御策略，具体如表3所示。

3.3 连锁故障博弈过程的收益函数

根据表2和表3所示的连锁故障过程，分别计算防御方未采取行动和采取行动时博弈过程的收益函数，计算结果如表4所示。

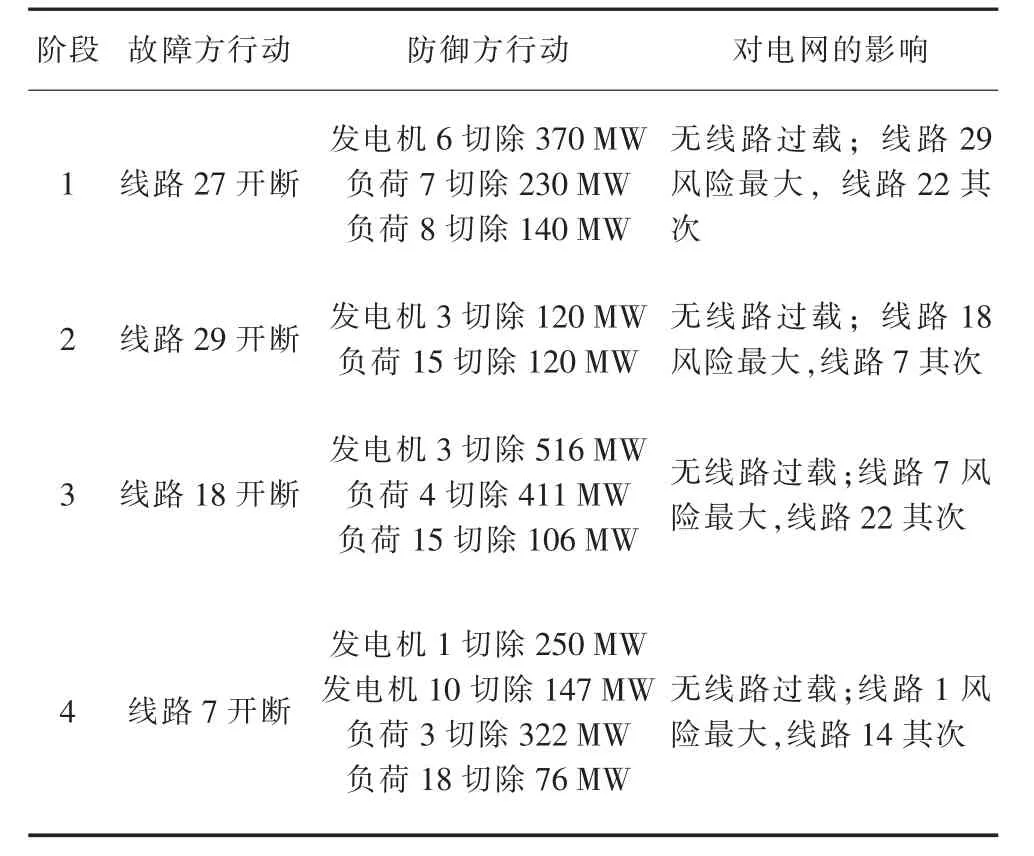
表3 线路27开断后的连锁故障多阶段动态博弈防御过程

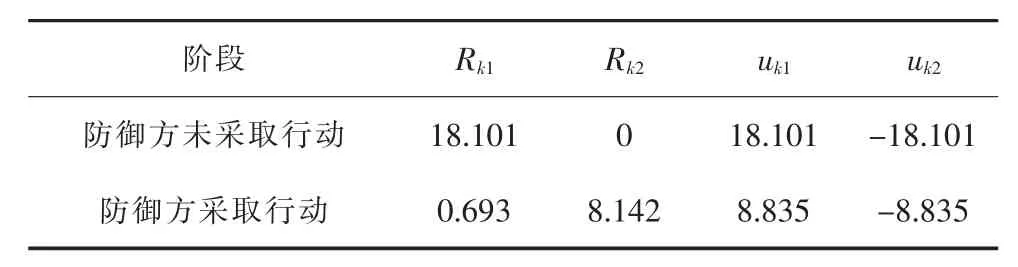
表4 博弈过程的收益函数对比

文献［16］指出，如果控制措施可使事件的风险降低，并且其控制代价小于风险降低的数值，则该控制可作为应对该事件的选项，并具有经济上的可行性。从表4可以看出，防御方采取行动后，故障方的停电风险收益降低了17.408，防御方的控制代价风险收益只增加了8.142，故障方的运行风险收益降低了9.266，因此本文的防御策略具有可行性。

4 结语

提出连锁故障多阶段动态博弈防御的要素和假设，构造了连锁故障的多阶段动态博弈防御模型。

综合考虑元件自身停运因素和潮流转移因素对元件停运概率的影响，提出元件实时停运概率表征有限理性的故障方不完美的选择能力；根据可掌握的事故状态信息，提出潮流转移严重度和系统失负荷严重度表征故障方追求自身利益的意识；基于风险分析方法，生成有限理性故障方的策略集合，帮助调度人员了解当前运行工况下最需关注的故障发展方向。

从风险理论的角度出发，将运行风险作为收益函数，不仅可以帮助调度人员了解故障带来的影响，还可以定量评估出控制措施的有效性。

［1］PSERC.Resources for Understanding the Moscow Blackout of 2005［EB/OL］.http：//www.pserc.wisc.edu/MoscowBlackowt.htm. 2005（7）.

［2］HINES P，BALASUBRAMANIAM K，SANCHEZ E C.Cascading failures in power grids［J］.IEEE Potentials，2009，28（5）：24-30.

［3］印永华，郭剑波，赵建军，等.美加“8.14”大停电事故初步分析以及应吸取的教训［J］.电网技术，2003，27（10）：8-11.

［4］丁理杰，江全元，包哲静，等.基于多智能体技术的大电网连锁跳闸预防控制［J］.电力系统自动化，2008，32（17）：6-11.

［5］张玮，潘贞存，赵建国.新的防止大停电事故的后备保护减载控制策略［J］.电力系统自动化，2007，31（8）：27-31.

［6］许婧，白晓民，黄镔.应对连锁故障的广域协同预控制系统研究［J］.电网技术，2013，37（1）：131-136.

［7］HOLMGREN A J，JENELIUS E，WESTIN J.Evaluating strategies for defending electric power networks against antagonistic attacks［J］.IEEE Transactions on Power Systems，2007，22（1）：76-84.

［8］CHEN G，DONG ZY，HILL D J，et al.Exploring reliable strategies for defending power systems against targeted attacks［J］.IEEE Transactions on Power Systems，2011，26（3）：1 000-1 009.

［9］吴广谋，吕周洋.博弈论基础与应用［M］.南京：东南大学出版社，2009.

［10］史慧杰，葛斐，丁明，等.输电网络运行风险的在线评估［J］.电网技术，2005，29（6）：43-48.

［11］吴旭，张建华，吴林伟，等.输电系统连锁故障的运行风险评估算法［J］.中国电机工程学报，2012，32（34）：74-82.

［12］薛禹胜.时空协调的大停电防御框架（二）广域信息、在线量化分析和自适应优化控制［J］.电力系统自动化，2006，30（2）：1-10.

［13］王安斯.基于事故链的电网脆弱性评估与稳定控制［D］.武汉：华中科技大学，2010.

［14］姚峰，张保会，周德才，等.输电断面有功安全性保护及其快速算法［J］.中国电机工程学报，2006，26（13）：31-36.

［15］滕林，刘万顺，貟志皓，等.电力系统暂态稳定实时紧急控制的研究［J］.中国电机工程学报，2003，23（1）：64-69.

［16］薛禹胜，肖世杰.综合防御高风险的小概率事件：对日本相继天灾引发大停电及核泄漏事件的思考［J］.电力系统自动化，2011，35（8）：1-11.

Multi Stage Dynamic Game Defense Model for Cascading Failures in Power System

LIU Jun1，WANG Jian2，LIAO Shuyang3，LI Yang4
（1.State Grid Huainan Power Supply Company，Huainan 232001，China；2.State Grid Chuzhou Power Supply Company，Chuzhou 239000，China；3.State Grid Anhui Maintenance Company，Hefei 230061，China；4.State Grid Bozhou Power Supply Company，Bozhou 236800，China）

Several blackout accidents have taken place both at home and abroad in recent years which caused by cascading failures.It is of great practical significance for the safety and the stable operation of power system to prevent the development of cascading failures and avoid the occurrence of blackouts.A model based on the multistage dynamic games with bounded rationality is proposed to defend against the blackout accident resulting from the cascading failures.Based on the hypothesis of bounded rationality of the fault and the correlation of its action，the component outage probability is proposed to betoken the imperfect selecting ability of the fault side with bounded rationality based on the real-time operating conditions，comprehensively considering the influence of the fault，external environment，power flow transfer，hidden failure and other factors on the component outage probability.Based on the possessed failure-state information，the severity of the power flow transfer and the load loss are proposed to represent consciousness of the fault side to pursue its own interests.The strategy sets are further generated on the basis of the risk analysis method.According to the risk theory，the operational risk is regarded as the payment function to quantify effectiveness of the action of the defense side.Finally，the IEEE 39-bus test system is chosen as an example to validate the rationality of the proposed model.

cascading failure；bounded rationality；multistage dynamic game；strategy set；payment function；power system

TM715

A

1007－9904（2017）05－0014－06

2016-12-07

刘军（1990），男，从事电力系统继电保护工作；王健（1990），男，从事电力系统继电保护工作；廖叔洋（1990），男，从事电力系统继电保护工作；李洋（1990），男，从事电力系统继电保护工作。