高强钢筋混凝土简支梁抗弯性能试验研究与数值计算★

郑如良 马 鸣

(1.解放军理工大学爆炸冲击防灾减灾国家重点试验室,江苏 南京 210007； 2.中国人民解放军69006部队，新疆 乌鲁木齐 830001)



高强钢筋混凝土简支梁抗弯性能试验研究与数值计算★

郑如良1马 鸣2

(1.解放军理工大学爆炸冲击防灾减灾国家重点试验室,江苏 南京 210007； 2.中国人民解放军69006部队，新疆 乌鲁木齐 830001)

通过对不同强度高强钢筋混凝土梁的加载试验，研究了高强钢筋对梁抗弯性能的影响规律，并运用有限元模拟软件MSC.Marc对试验中的不同试件进行模拟，对比了所得的试验值和模拟值，结果表明：高强钢筋对提高梁的承载力效果十分显著，梁的屈服挠度和破损荷载也随钢筋强度提高呈增大趋势。

高强钢筋，混凝土简支梁，抗弯性能，MSC.Marc

1 试验概况

1.1 试件设计

试验主要是对高强钢筋混凝土梁进行弯曲试验，梁的尺寸取为1 800 mm×300 mm×150 mm，梁的支撑跨距为1 500 mm。试验机的最大载荷为4 000 kN，满足试验要求。

试验主要考虑不同等级的钢筋、不同配筋率和不同等级的混凝土梁，主筋配筋率为0.6%和1.0%两种，受拉主筋为HRB400，HTB600和HTB700三种，混凝土为C40和C60两种，主要针对HTB700级钢筋开展试验。各组试件编号见表1。

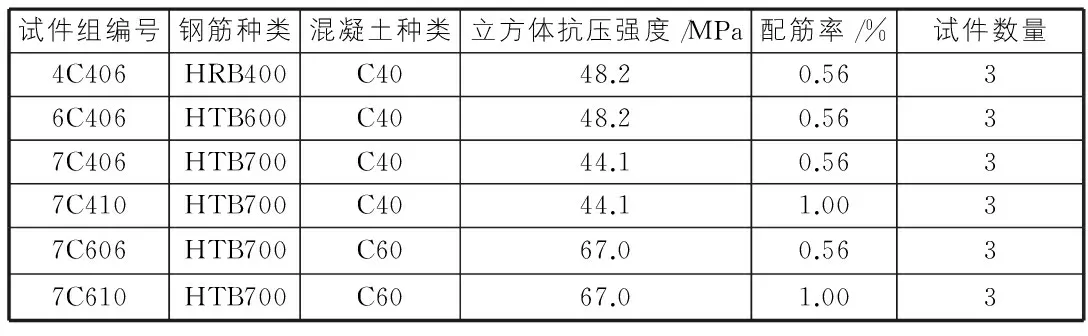
表1 试验安排表

试件的配筋方式见图1，采用两根受拉主筋和两根构造筋，中部纯弯段受压区没有钢筋，试件混凝土保护层厚度为25 mm。试件梁的实际配筋率见表2。

表2 试件实际配筋率

截面尺寸/mm受拉主筋配筋率/%箍筋配箍率/%150×3002ϕ120.562ϕ6@1000.38150×3002ϕ161.002ϕ6@600.63

1.2 试验设计

1)加载方式。试验在试件三等分点处加载，加载方法见图1。采用分级连续加载方法，加载程序参考GB/T 50152—2012混凝土结构试验方法标准[1]确定，在达到试件屈服荷载Fs前，每级加载不大于0.2Fs；在达到试件开裂荷载前，每级加载值约为0.1Fs；接近开裂荷载计算值时，每级加载值约为0.05Fs；试件开裂后，每级挠度增量值在0.1Fs～0.2Fs之间取值；试件屈服后，按照挠度增量控制加载，每级挠度增量约为3 mm～4 mm。每级荷载持续时间不少于5 min。

2)测点布置。在梁跨中位置布置位移传感器(y)测量试件跨中挠度，支座处布置百分表测量支撑钢梁在支座处的沉降，用于修正挠度测量值。力传感器(F)固定在分配钢梁上，用于测量试件承受的总荷载。

2 Marc有限元数值模拟

2.1 单元模型

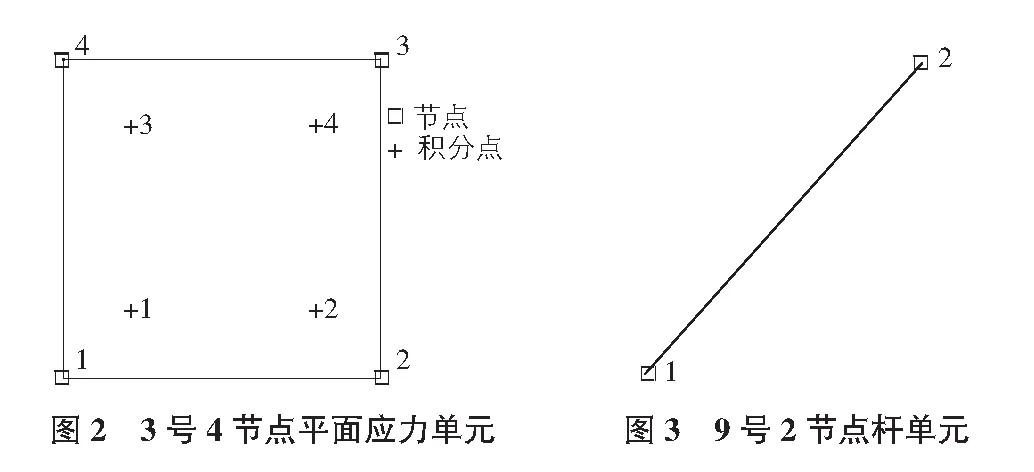
混凝土被认为是连续均匀材料，使用4节点、等参、任意扭曲连续四边形平面应力单元(PLANE STRESS-3号单元)[2]，用单元厚度表示梁的宽度。单元每个节点有两个自由度即x和y方向的平动自由度，使用双线性插值函数描述位移，该插值函数为：x=a0+a1ξ+a2η+a3ξη，单元和积分点的几何特征见图2。

钢筋采用二节点杆单元(truss，9号单元)[2]，该单元节点有两个方向的平动自由度，只能承受轴向力，没有抗弯刚度，采用线性位移插值函数：ψ=ψ1ξ+ψ2(1-ξ)，其中，ψ1,ψ2均为节点处的位移值，ξ(0≤ξ≤1)为正交化坐标。用杆单元的截面面积表示钢筋的面积，单元和积分点的几何特征见图3。

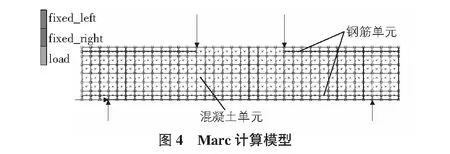
试验中梁由钢筋和混凝土组合而成，钢筋置于混凝土中，钢筋的相对体积较少，但弹性模量相对较大，模拟中采用分离式模型，本试验粘结较好，模拟中不插入粘结单元[3]。本次试验为钢筋混凝土简支梁，试件主要为受弯破坏，模拟中忽略箍筋作用，并将构件简化为平面模型，但与构件尺寸一致，选用四边形单元，网格尺寸大小为50 mm。试件所受重力对跨中弯矩贡献很小，模拟中忽略重力影响。在模型左端支座处施加x,y,z三个方向约束，右端支座施加y,z两个方向约束，并在与试验相同的位置施加竖向集中荷载，模型、网格划分及边界条件见图4。

2.2 材料模型

1)混凝土本构关系模型。混凝土是拉压异性的脆性材料，抗拉强度远低于抗压强度。根据GB 50010—2010混凝土结构设计规范[4](以下简称规范)，混凝土单轴受压的应力应变曲线按下列公式确定：

σ=(1-dc)·Ecε。

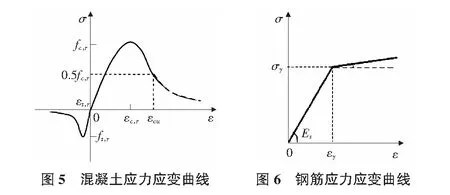
混凝土材料极限拉应力按规范取ft=0.88×0.395(fcu0)0.55×(1-1.645δ)0.45×αc2，极限压应力取fc=αc1αc2fcu0，其中，αc1，αc2按规范取值。根据《建筑抗震弹塑性分析》[5]，软化模量设为弹性模量的1/10，混凝土极限压碎应变设为0.003 3，裂面剪力传递系数取0.2。混凝土应力应变曲线关系如图5所示。

2)钢筋本构关系模型。在钢筋混凝土结构中，钢筋处于单轴受力状态，应力应变关系相对来说比较简单，数值模拟中采用弹塑性双斜线模型。如图6所示，当σ<σy时，钢筋处于线弹性阶段，弹性模量为Es。当σ=σy时钢筋进入塑性，进入屈服阶段后，弹性模量取1/10Es。

2.3 分析求解方法

混凝土是非线性材料，模拟中采用载荷增量法[6]进行分析。模拟采用力加载和位移加载两种方式进行，把给定荷载分成若干段，从零开始逐段进行分析处理，在每个荷载段上使用牛顿—辛普森迭代法。载荷增量法的优点是，只要保证载荷增量足够小，就可以保证解得收敛性和合理性。

3 数据分析

试验与模拟对比分析：

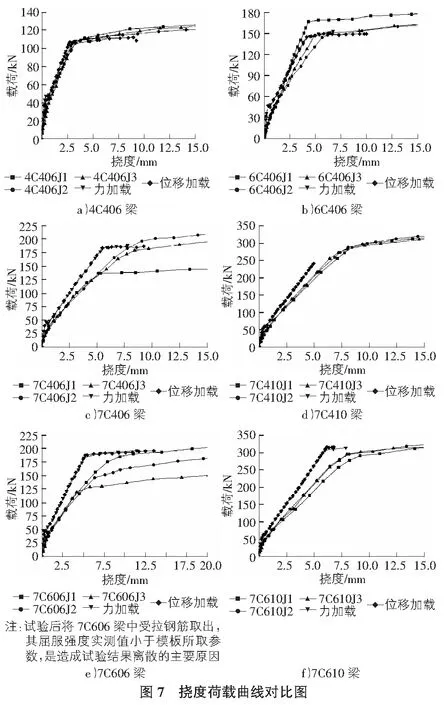
将试验，数值模拟和理论计算得到的载荷挠度曲线，用origin软件绘制在同一直角坐标系中，进行对比分析，如图7所示。

结合挠度荷载曲线，将试件在各个不同加载阶段的荷载和挠度以及钢筋屈服应变的试验值(取每组试验3个试件的平均值)和模拟值进行汇总，列入表3中。

表3 试验和模拟结果对比分析表

由试验结果表明：

1)开裂荷载随混凝土强度的提高而增大，却不因钢筋强度改变发生变化；

2)屈服荷载、极限荷载均随钢筋强度的提高和配筋率的增大而增大；

3)屈服挠度和极限挠度均随钢筋强度的提高而增大，屈服挠度同样随配筋率增大而增大，但极限挠度却随配筋率增大而减小。

由图7和表3对比分析可得：

1)在正常的配筋范围内，从开始加载到钢筋屈服后的一段时间内，模拟所得的载荷—挠度曲线和载荷—钢筋应变曲线与试验结果比较吻合，计算的屈服荷载和钢筋屈服应变误差一般不超过10%，极限荷载误差一般也在20%以内。

2)部分相对配筋率较高的试件，钢筋还未屈服便出现不收敛现象，但试验仍为适筋破坏，未能对这部分试件作出有效模拟。

3)本文模拟采用了力和位移两种加载方式，两者所得结果大致相同。但相对而言，力加载计算所得的屈服挠度和屈服荷载更接近试验值，而位移加载更便于在未知承载能力的情况下对构件进行评估。

4 结语

1)试验表明高强钢筋混凝土梁开裂荷载随混凝土强度的提高而增大，却不因钢筋强度改变发生变化；屈服荷载、极限荷载均随钢筋强度的提高和配筋率的增大而增大；屈服挠度和极限挠度均随钢筋强度的提高而增大。

2)Marc有限元模拟的方法可以较好的模拟简支梁加载到屈服的过程，与试验结果比较接近。相对而言，力加载计算所得的屈服挠度和屈服荷载更接近试验值，而位移加载更便于在未知承载能力的情况下对构件进行评估。两种方式均能够准确得到试件的承载力，可以作为评估高强钢筋混凝土梁承载和变形能力的有效手段。

[1] GB/T 50152—2012，混凝土结构试验方法标准[S].

[2] Marc 2005 Help，Volume B: Element Library[Z].

[3] Marc 2005 Help，Volume A: Theories and User information[Z].

[4] GB 50010—2010，混凝土结构设计规范[S].

[5] 陆新征，叶列平，缪志伟，等.建筑抗震弹塑性分析—原理、模型由于在ABAQUS，MSC.MARC和SAP2000上的实践[M].北京：中国建筑工业出版社，2009.

[6] 马士忠.钢筋混凝土梁的非线性有限元分析和变形能力计算[D].长沙：湖南大学，2008：25-29.

Experimental study and numerical analysis on the flexural performance of high-strength simply supported reinforced concrete beam★

Zheng Ruliang1Ma Ming2

(1.State Key Laboratory of Disaster Prevention and Mitigation of Explosive and Impact, PLA University of Science and Technology, Nanjing 210007, China; 2.PLA 69006 Troop, Urumqi 830001, China)

Through the different high strength reinforced concrete beam load test, study of the effect of high-strength steel to flexural performance of beams. Use the finite element simulation software MSC.Marc analyze different specimens, and the experimental results and the simulated values are compared and analyzed, test showed that: the effect of high-strength steel to improve the bearing capacity of the beam is very significant, yield beam deflection and breakage load is improved also with steel strength tended to increase.

high-strength steel, concrete simply supported beam, flexural performance, MSC.Marc

1009-6825(2017)08-0034-03

2017-01-06★：国家创新研究群体科学基金项目(51021001)

郑如良(1991- )，男，在读硕士

TU311

A