大跨超长类结构多点激励输入地震动应用研究★
吴 边 张 敏
(四川建筑职业技术学院,四川 德阳 618000)
·结构·抗震·
大跨超长类结构多点激励输入地震动应用研究★
吴 边 张 敏
(四川建筑职业技术学院,四川 德阳 618000)
围绕合理确定大跨、超长类结构的多点激励输入地震动这一问题,对当前在应用相干函数模型及多点地震动合成中遇到的一些问题作了研究,分析了相干函数模型的适用性,并给出了H-V模型和Qu模型在相干程度下的参数取值,基于Hao方法,归纳了空间地震动的人工合成方法。
多点激励,相干函数模型,地震动合成,大跨结构
0 引言
近年来我国建成了大量的大跨,超长类结构工程,该类结构大多建设在地震区,有的甚至是在高烈度区,结构的抗震问题突出;而且,该类结构往往担负着重要功能,如大跨度桥梁、航站楼、输电塔线等,若出现地震后结构失效会造成不可估量的损失;因此,对大跨、超长类结构的抗震设计就显得尤为重要[1]。
由于大跨、超长类结构属于空间延展结构,结构所处区域范围广,场地条件变化较大。在对该类结构进行动力时程分析时,若仍采用一致地震动输入会产生较大误差,更为合理的方法是采用能在一定程度上反映地震动的空间变化特征的多点激励地震动输入。当前对行波效应考虑较成熟,也有规范可循;然而在实际工程中对相干效应和局部场地效应的考虑很少。本文主要就针对如何确定合理的多点激励输入地震动加以研究,并给出了一套相应的方法,能够为大跨、超长类结构在确定输入地震动的问题上提供参考。
1 多点激励输入地震动应用现状
目前对大跨、超长类结构考虑空间效应的地震响应分析方法有修正反应谱法,随机振动分析方法,时程分析法。由于前两类分析方法在考虑地震动空间效应时有较大的局限性,而时程分析方法计算原理成熟,商用有限元分析软件(如SAP2000,MIDAS等)中可直接使用,在实际工程中应用广泛。为了在时程分析中考虑地震动的空间变化,逐渐发展出一套多点激励的时程分析方法;多点激励即在结构的各个支承点输入具有空间相关性的一组地震波,而非同一条地震波。该类方法较传统的一致输入的分析方法,可在一定程度内考虑地震动的空间变化,其考虑程度取决于采用的地震动空间变化模型。
从当前我国在大跨类工程的实践来看,在选择输入地震动时,若要完整地考虑地震动的空间变化全部因素,还不成熟;其中对相干函数模型的选择问题尤为明显。其中一个突出的矛盾是抗震分析需要计算多组“相干程度”工况,然而,除极个别研究者[6]外,绝大多数相干函数模型没有给出多工况下相应的参数取值。
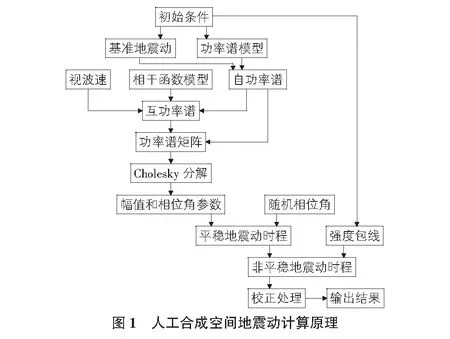
为解决以上问题,本文以地震动台阵记录为依据研究了多点激励输入地震动合成中的有关问题,并给出了一套合成方法(见图1),最后通过算例加以验证。
2 多点激励输入地震动合成
大跨、超长类结构时程分析的第一步就是确定合理的多点输入地震动。虽然是采用真实的差动台阵记录较为可靠,然而在工程应用很难实现。对多点输入地震动而言,最佳的解决办法是人工合成多点地震动的方法。
2.1 自谱密度估计
已知实际地震动记录,可采用Welch修正周期图法得出自谱密度。若未给出实际地震动,则基于过滤白噪声过程,采用功率谱(自谱密度)模型,当前较多采用的是改进K-T功率谱模型(杜修力、陈厚群[7])。
2.2 相干函数模型分析
考虑到当前提出的相干函数模型较多(见表1),就存在相干函数模型的选择性问题。本文首先针对实际台阵记录,对不同的相干函数模型参数加以拟合,根据拟合效果(均方差、残差平方、拟合优度系数)判定各模型的通用性,最后选取了2种相干函数模型。
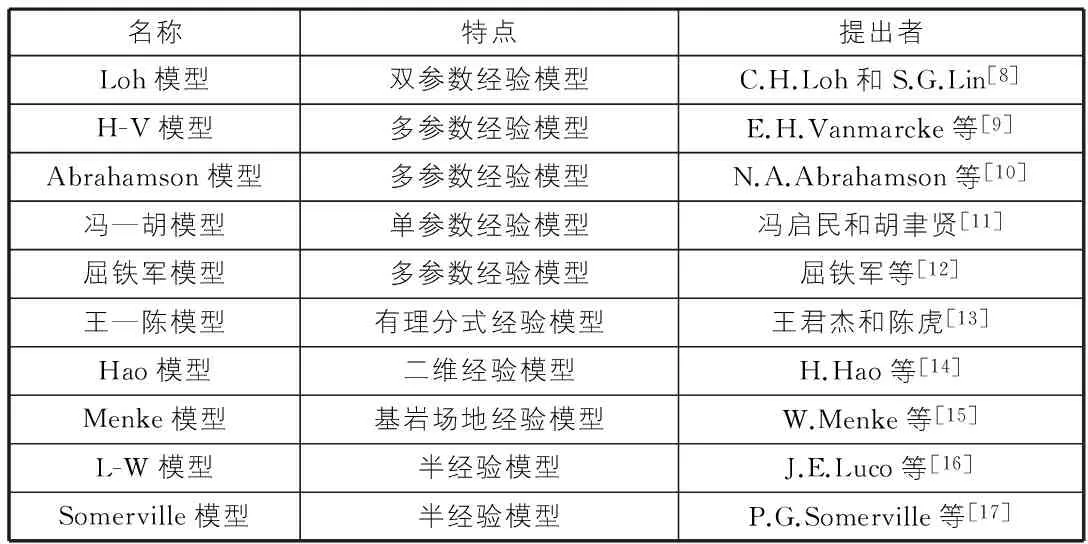
表1 相干函数模型统计
1)Harichandran-Vanmarcke模型(以下称H-V Model)。
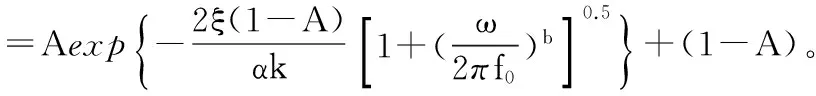
参数取值:A=0.736;k=766;f0=1.09;b=2.78。
2)屈铁军模型(以下称QuModel)。
|γ(ξ,ω)|=exp[-a(ω)ξb(ω)]。
其中,a(ω)=a1ω2+a2;b(ω)=b1ω+b2。
参数取值:a1=0.000 016 78;a2=0.001 219;b1=-0.005 5;b2=0.767 4。
2.2.1 模型参数拟合
以SMART1台阵在1986年11月14日记录的Event45为例(见图2),给出模型参数的拟合过程。
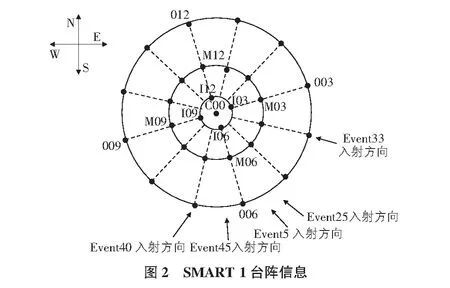
任意选取某一参考台站(本文选择I06)其他非参考台数据站与其共同构成样本点。选择方法:台站基本处于一个方向;各个台站间的距离应该差别明显,因此不宜在相似的距离选择多个台站;总的选择数量不能太多,选择多了会使拟合结果出现较大的离散性。根据上述原则,确定了4组台站拟合样本(I06~I07,I06~C00,I06~I12,I06~M06),样本点取平滑过后的值。参数估计采用UniversalGlobalOptimization算法,回归计算采用Levenberg-Marquardt算法,达到收敛标准后,得出最终参数取值。
2.2.2 模型参数统计分析
借鉴抗震规范中统计设计反应谱的思路,采用两次拟合的方法进行参数统计分析(总共统计了1 254组地震动记录)。表2给出了H-VModel和QuModel模型3组代表三种“相干度”的参数取值建议。
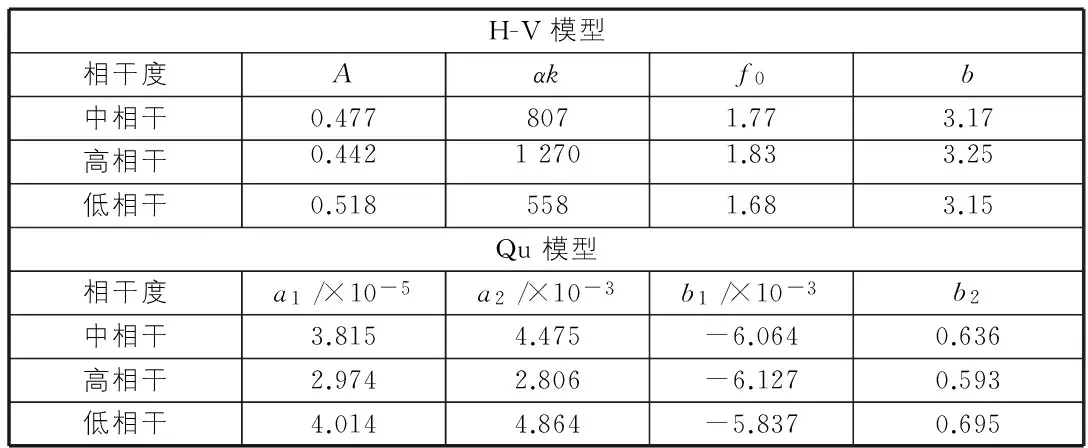
表2 相干函数模型参数取值建议
2.3 空间地震动合成
空间地震动的时空序列描述可以用谱密度矩阵来表示:
其中,[S(iω)]为对称正定阵Hermite矩阵,对[S(iω)]进行Cholesky分解得到:
[S(iω)]=[L(iω)][LH(iω)]。
则有:
其中,第n点的地震动时程可表示为n项三角级数之和(Hao[14]);
(1)
Anm(ωk)和θnm(ωk)与谱密度矩阵之关系,可表达为(屈铁军等[12]):
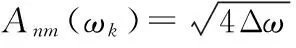
由于式(1)无法考虑和后面生成点的相关性,将式(1)写成离散的形式:
(2)
其中,l为时间;m为地点;k为频率。对式(2)进行离散Fourier变换:
(3)
在计算机编程时,通过式(3)先生成Fourierspectrum,然后使用InverseFourierTransform得到最终的地震动时程。
3 算例分析
根据上节所述方法,在Matlab中编制计算程序MulPoint,根据不同的合成初始条件来合成(图3中1为已知天然波,2为无天然波,3为已知功率谱模型)。
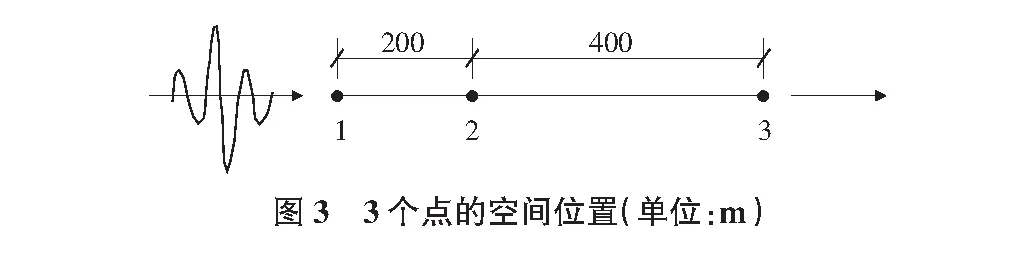
1)条件1。初始地震动选择SMART1台阵的Event45事件中C00台站记录到的EW水平地震波分量。假定视波速500m/s。采用H-V模型(中相干程度)。分段强度包线模型:
2)条件2。Ⅰ类场地,8度设防烈度,设计地震分组第3组,结构的阻尼比ξ=0.05。杜修力—陈厚群模型。其他同条件1。
图4,图5分别给出了合成地震动的功率谱和相干函数值,从图中可以看出,无论是采用哪一种初始条件,从地震动的功率谱来看,S1,S2,S3差异很小,与初始条件(C00或功率谱模型)差异也不大,是比较合理的;从吻合相干函数模型的情况来看,也是吻合很好的;总的来说,最终合成效果理想。
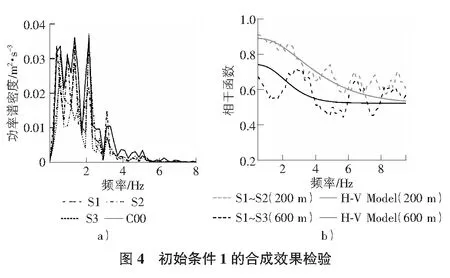
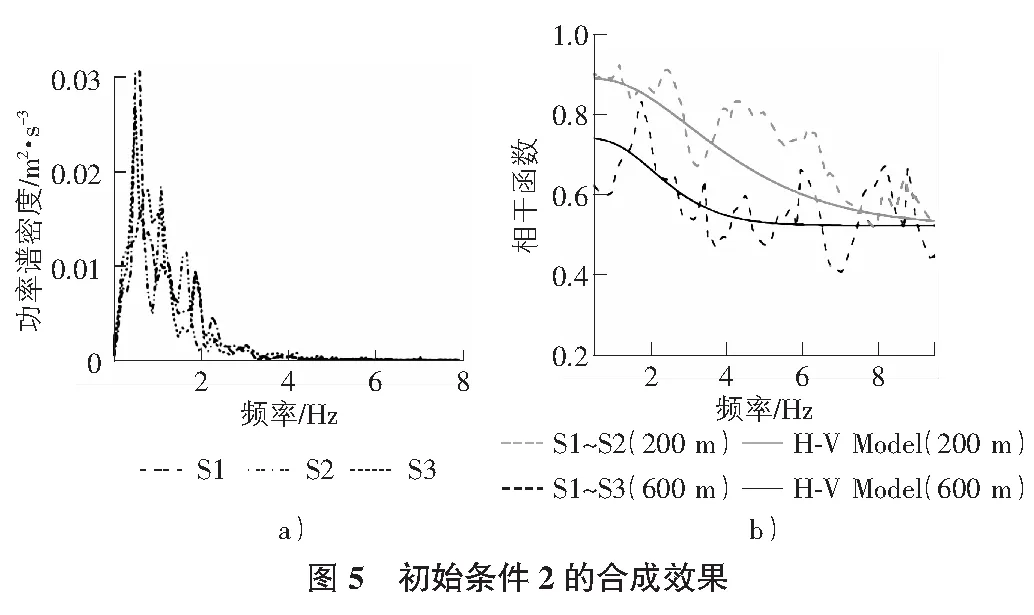
4 结语
围绕合理确定大跨、超长类结构的多点激励输入地震动这一问题。对相干函数模型的应用以及多点地震动合成中遇到的一些问题加以研究。主要工作和结论可归纳为:
1)在实际地震动差动台阵记录的拟合结果的基础上,对比了当前较普遍的相干函数模型,给出了其中的H-V Model和Qu Model的考虑不同相干度的参数取值建议。
2)基于不同的初始条件(已知基准地震动、功率谱模型)给出了多点激励地震动的人工合成方法,并通过算例加以初步验证。
[1] 李英民,刘立平.工程结构的设计地震动[M].北京:科学出版社,2011.
[2] Newmark N M, Rosenblueth E. Fundamentals of earthquake engineering[J]. Civil engineering and engineering mechanics series,1971(12):76.
[3] 赵基达,蓝 天.中国空间结构三十年的进展及今后展望[J].工业建筑,2013(4):131-138.
[4] 全 伟.大跨桥梁多维多点地震反应分析研究[D].大连:大连理工大学,2008.
[5] 白凤龙.空间变化地震动激励下大跨度结构的反应研究[D].大连:大连理工大学,2010.
[6] Kaiming B,Hong H,Nawawi C. Required separation distance between decks and at butments of a bridge crossing a canyon site to avoid seismic pounding[J]. Earthquake Engineering Mechanics,1986,112(2):154-174.
[7] 杜修力,陈厚群.地震动随机模拟及其参数确定方法[J].地震工程与工程振动,1994(4):1-5.
[8] Loh C H. Analysis of the spatial variation of seismic waves and ground movements from smart-1 array data[J]. Earthquake engineering & structural dynamics,1985,13(5):561-581.
[9] Harichandran R S, Vanmarcke E H. Stochastic variation of earthquake ground motion in space and time[J]. Journal of Engineering and Structural Dynamics,2009,39(3):303-329.
[10] Abrahamson.N.A,Schneider.J.F,Stepp.J.C Empirical spatial coherency functions for application to soil-structure interaction analyses[J]. Earthquake spectra,1991,7(1):1-27.
[11] 冯启民,胡聿贤.空间相关地面运动的数学模型[J].地震工程与工程振动,1981,1(2):1-8.
[12] 屈铁军,王君杰,王前信.空间变化的地震动功率谱的实用模型[J].地震学报,1996(1):55-62.
[13] 王君杰,陈 虎.面向设计应用的地震动空间相干函数模型[J].地震工程与工程振动,2007(1):16-23.
[14] Hao H, Oliveira C S, Penzien J. Multiple-station ground motion processing and simulation based on SMART-1 array data[J]. Nuclear Engineering and Design,1989,111(3):293-310.
[15] Menke W, Lerner-Lam A L, Dubendorff B, et al. Polarization and coherence of 5 to 30 Hz seismic wave fields at a hard-rock site and their relevance to velocity heterogeneities in the crust[J]. Bulletin of the Seismological Society of America,1990,80(2):430-449.
[16] Luco J E, Wong H L. Response of a rigid foundation to a spatially random ground motion[J]. Earthquake engineering & structural dynamics,1986,14(6):891-908.
[17] Somerville P G, Mclaren J P, Saikia C K, et al. Site-specific estimation of spatial incoherence of strong ground motion[C]. ASCE,1988.
Applied study on inputted multi-point ground motions of long-span structures★
Wu Bian Zhang Min
(Sichuan College of Architectural Technology, Deyang 618000, China)
On the issue of identifying the multi-point ground motions of the large-span and super-long structures, the paper researches some problems in the application of the coherence function model and the integration of multi-point, analyzes the adaptability of the coherence functions, undertakes the parameter value with H-V model and Qu model under the coherence, and sums up the manual integration method of the space motion.
multi-point motion, coherence function, motion integration, large-span structure
1009-6825(2017)08-0023-03
2017-01-04★:四川建筑职业技术学院科研项目(2016KJ03)
吴 边(1987- ),男,硕士,助教; 张 敏(1989- ),女,硕士,助教
TU318.1
A

