“M1的M2倍”格式的认知分析
谢文杰(安徽大学,安徽 合肥 230000)
“M1的M2倍”格式的认知分析
谢文杰
(安徽大学,安徽 合肥 230000)
数量关系“M1的M2倍”这种格式,其中“M”表示数词,例如“三的五倍”“十一的十一倍”等这类结构,使用“的”字结构的偏正结构去描写,但与其相关或者相对的别的数量关系,却有的可以用这种偏正结构去描写,有的不可以用。文章通过对“M1的M2倍”这种格式的形式分析,并运用隐喻、整合度的认知语言学概念,去探求这种偏正结构表达式的特殊性,同时也尝试探求这种数量关系用偏正结构表达背后所隐藏的认知机制。
“M1的M2倍”;偏正结构;隐喻
引言
从认知的角度去分析一些特定的短语结构已不是什么新鲜事。前贤们从“概念隐喻”“概念整合”“范畴化”等认知理论对各种格式的短语进行分析,如“又A又B”“连V1带V2”等。而本文所要分析研究的对象是 “M1的M2倍”这种格式,其中“M”表示数词,例如“三的五倍”“十一的十一倍”等这类结构。虽然这种结构没有引起前贤们的足够关注,但笔者认为“M1的M2倍”这种偏正结构有一定的特殊性,更为重要的是,为什么这种偏正构造可以用来表示 “M1的M2倍”其内在的数量运算关系?需要符合哪些条件?本文将尝试从概念隐喻、概念整合等理论着手加以分析。
1 “M1的M2倍”的形式考察
1.1 “倍”的性质
根据《汉语大字典》[1]对于“倍”的解释来看,大致可分为三类词性:
1.1.1 动词。首先“倍”通“背”,有背叛、违背、背诵等“背”的字义。如《左传·韶公二十六年》:“倍奸齐盟”,孔颖达疏:“倍,即背也”;其次是动词,增加、加添之意。如《左传·僖公三十年》:“焉用亡郑以倍邻”,杜预注:“倍,益也”。“倍”作动词的用法在现代汉语已经基本不用了。
1.1.2 副词。修饰动词,越发、更加的意思。如在“每逢佳节倍思亲”中做副词修饰动词“思”,还有在“倍儿爽”“倍儿精神”等修饰形容词。显然,“M1的M2倍”中不存在能让副词“倍”修饰的部分,因此“倍”在此结构中不可能是作为副词使用的。
1.1.3 量词。跟在数词之后的粘着词[2],如《过秦论》中“尝以十倍之地,百万之师,叩关而攻秦”,“倍”就表示量词,即表示某数成几倍增加。凭借“M2”的数词词性,也可以判断出“倍”的量词词性。刘立根据何杰的《现代汉语量词研究》和张斌的《新编现代汉语》把量词分为六大类[3]:“名量词、动量词、时量词、倍率量词、兼职量词、复合量词”。而“M1的M2倍”中的“倍”是就是属于“倍率量词”。
1.2 “M1的M2倍”的句法功能
“M1的M2倍”格式嵌入句后主要充当以下成分:
1.2.1 充当主语:
例a.瞄一眼,回复:2的2倍是八!
例b.“十的二倍是多少?”“二——十”父亲听了突然转笑为哭,是欢喜的哭。
例c.要不是妖魔的化身,又岂会懂得二的一倍就是四,四的一倍就是八?
1.2.2 充当宾语
例a.这一天最受欢迎的是当年满12岁的男孩,12是6的两倍,可称六六顺。
例b.我想了想,回答他:“那就说是0.5的2倍,2的二分之一。”
例c.为达到以上平衡,从表p知,溶液pH为8.21的35倍浓透析液。
1.2.3 整体作为数词跟量词搭配
例a.据说整个宇宙的星星总共有一千亿的一千亿倍颗,但我所能够看到的最漂亮的星星,就是这一刻,停留在我的天花板上的星星。
例b.下周就是7的2倍周期第14周,江恩时间定理已到了极限之顶端。从历史角度看,应该是回转向上周期已经不容怀疑。
可以看出,“M1的M2倍”作为一个“类固定短语”[4],即结构模式比较固定、短语意义比较单一,同时句法功能也相对单调。在统计的近100条有效语料中,作为含有“是”“为”这类判断句的主语或者宾语占到90%以上,而把短语整体当中一个数词来与量词合成数量词则占很小的比例。
1.3 “M1的M2倍”与偏正结构
1.3.1 “M1的M2倍”可以看成一个“数词+ 的+数量词”的偏正结构,但“M1的M2倍”这种数量运算性的偏正结构存在着一定的特殊性——中心语的隐藏性。
以“三的五倍”为例:
a1.这是我们的家-这是我们-这是家
a2.这是三的五倍-这是三-这是五倍?
b1.计算火箭的速度-计算火箭-计算速度
b2.计算三的五倍-计算三-计算五倍?
c1.增加合格的防腐剂-增加合格-增加防腐剂
c2.增加三的五倍-增加三-增加五倍?
朱德熙曾说“谓语动词会对偏正结构的中心词会产生作用”,所以我们在“三的五倍”前面加上一些非判断句的谓语成份,能够看出a1、b1和c1中的谓语动词的语义指向基本上还是指向了中心语,而a2、b2和c2中的谓语动词既不是直接指向“的”前面的数词M1,也不能指向“的”后面的M2。由此可见,“M1的M2倍”这个结构内部有着很强的关联性,其核心即不像是“M1”,也不是像“M2倍”。但是,从短语整体进行分析,“M1的M2倍”这类结构一般充当主语和宾语,是名词性词组。根据布龙菲尔德的“向心结构理论”[5],人们是根据偏正结构的整体功能跟其直接组成成分功能的异同来决定中心语所在的。也就是说,偏正结构的整体功能必须和它中心语的功能相同。而位于中心语位置的数量词“M2倍”也是名词性成份,看以下几例:
a.年关临近,茅台酒继续涨价,53度飞天茅台酒在上海很多门店的售价已经高达每瓶2000元,几乎是厂家零售指导价1099元的两倍,茅台酒厂的“限价令”已是“传说”。
b.0时1分,支付宝付款笔数瞬间超过5.5万笔,是前一分钟的10倍。
c.这就差不多了价格是普通一杯的7倍。
朱德熙对于名词的语法特点解释是:“可以受数量词修饰;不受副词修饰”。通过例子可以看出“M2倍”是可以受数量词的修饰(1099元的两倍、前一分钟的10倍),同时也不受副词修饰(*很十倍、*早三倍、*不七倍),可以看出“M2倍”是名词性成分,与“M1的M2倍”这个偏正结构的整体功能一致,同时也处于中心语的位置上,所以偏正结构“M1的M2倍”的中心语应该是“M2倍”。
1.3.2 根据朱德熙对偏正结构的分类来看,“三的五倍”这种偏正结构还存在别的特殊性——修饰关系的不确定性
从形式上看,在这个结构中数词做修饰语,用来修饰后面的名词性成分。但是这种修饰又是怎样一种“修饰”呢?我们知道数词一般和量词组合在一起才能起到修饰名词的作用,而且一般不带“的”,如“五张纸”“两本书”。数词一般情况下无法单独修饰名词。但有一些特例,如“杭州八景”“江南七怪”等这样的古代汉语用法。首先我们可以把“M1的M2倍”格式单纯看作修饰语表示数量,比如“三的五倍”,“三”就是对“五倍”这样的倍数关系的一个“定量修饰”,即确定后面中心语的某种数量值。其次,我们也可以把“M1的M2倍”格式看出一个领属结构,“M2倍”受“M1”支配,即“三的五倍”中“五倍”是受到“三”的支配。不管看成什么修饰关系,“三的五倍”都蕴含着抽象的数学运算关系,即“M1的M2倍→M1*M2(*表示乘)”。笔者认为正是因为“M1的M2倍”中的偏正关系映射到其抽象的数学运算关系中,才使得“M1的M2倍”格式产生了特殊性,也就是隐喻产生的作用。
2 “M1的M2倍”格式的隐喻机制
2.1 概念隐喻
Lakoff曾经明言 “让他从生成语法学派彻底转向认知语言学的一个重要契机便是七十年代末 Reedy所发现的 ‘管道隐喻 (The Condiut Metaphor)’”[6]。足以说明隐喻理论对于认知语言学甚至对于整个语言学界的影响。“A is B”(time is money)这类典型的隐喻表达,传统理论将其视为一种语言修辞现象,但在语言学家Lakoff和哲学家Jhonson出版了 《Metaphor We Live By》[7]后,越来越多的人认识到隐喻是一种认知方式,而且是一种广泛的潜移默化的根深蒂固的认知方式。以一个认知域来认识和理解另一个认知域,且这还是人们认识世界、组织思维、进行推理、建构语言等须臾不可缺少的心智机制,从而形成 “隐喻认知理论”(Cognitive Theory of Metaphor),又叫 “概念隐喻理论”(Conceptual Metaphor Theory)[8]。Lakoff和Johnson把概念隐喻分为三类:
2.1.1 结构性隐喻(Structural Metaphors)。就像“time is money”“life is journey(人生是旅行)”这类隐喻,转用的不仅是概念域中的单个概念,而是把一个概念域中的多种语义结构系统地映射到另一个概念域。
2.1.2 方位性隐喻(Orientational Metaphors)。“它不是用一个概念去构造另一个,而是在同一个概念内部,运用人类基本的空间方位感知能力,通过参照上下、内外、前后、深浅、中心-边缘之类的空间方位自相组织起来的”[9]。如“I’m feeling up(我感觉好极了)”,“I’m feeling down(我情绪很低)”,“up”和“down”都是方位概念,借助这样基本的方位概念去表示抽象的情绪,显得十分自然。
2.1.3 本体隐喻(Ontological Metaphors)。如同方位感知是人类的基本能力一样,人类对物理世界里的实体及物质的经验感知也是非常基本的能力,我们据此可以理解那些较为抽象的经验,如事件、行为、感觉、观念等,将它们视为离散的、有形的实体,以便对之进行推理。 简单来说就是,用具体物体概念域来认识和理解另一个(抽象)概念域。
笔者认为“M1的M2倍”这种数量结构的偏正描写是一种结构性隐喻。“的”字偏正结构内部所包含的复杂语义结构作为源域(source domain)映射给了数量关系描写的结构即目标域(target domain),不仅是单一的概念的映射,而是结构内部复杂语义组合的映射。
2.2 两个条件
“M1的M2倍”所表达的是一种抽象的数量运算关系,其内在的数量关系可以用关系式“M1*M2”来表示(*表示乘以)。“M1*M2”这种数量运算是抽象的、不易理解的,而在实际日常语言的表达方式中,我们经常用偏正关系 “M1的M2倍”去表达和理解“M1*M2”这种抽象的数量运算关系,也就是用偏正关系这个概念域去映射数量关系这个概念域。这两个概念的认知域自然是不同的,但它们的语义结构存在着有规律的对应关系。
2.2.1 扩充性
首先,偏正结构都是修饰语对于中心语的扩充。从语义上来说,不管是怎样的修饰,都是对于中心语信息量的增加。如“我们的学校”是对“学校”领属者的增加说明;“木头房子”是对“房子”属性的增加说明;“喝水的杯子”是对“杯子”用途的增加说明,可见偏正结构本身是带有增加、扩充的属性。而“M1*M2”所代表的乘法运算也是一种增加、扩充的运算。同样拥有扩充性的还有指数运算,即“M1M2”,也可以用“M1的M2次方”这样的偏正结构来表达。这也就解释了为什么相对于乘法来说,“M1/M2(/表示“除以”)”这种除法运算无法用偏正结构表示,只能用“M1除以M2”这种方式表示。但是,如果把除法转换成乘法,还是可以使用偏正结构表示,如 “4/2”可以转化为“4*1/2”,就可以表示成“4的1/2”。可以看出,数值运算最后的结果不管是增多了还是减少了,只要运算方法是正向的(乘法、指数之类),都可以用偏正结构表示。这更说明,数量关系这个域中的增加、扩充属性是认知上的,并非是严密理性的计算得来,和偏正关系中的扩充性有着认知上的对应关系。
2.2.2 概念整合度
Fauconnier最早主张用 “心智空间”(Mental Space)和 “概念整合理论”(Conceptual Blending Theory)[10]来解释人类进行范畴化、建构认知模型和理解自然语言意义的过程。“概念整合”是一种极为普遍的认知过程,沈家煊认为“其在自然语言的意义建构过程中具有重要的作用,事实上语言的意义不是通过组合而是通过整合获得的”[11]。“概念整合”指的是对两个来自不同认知域的概念有选择地提取部分意义整合起来进而形成一个复合概念结构的过程,简而言之就是——整体大于部分之和。
前面说用偏正关系这个概念域去映射正向增加的数量关系这个概念域,是因为这两个概念的认知域都存在着增长、扩充的属性。但“M1+M2”这类加法数量关系却无法用偏正结构表示,只能用“M1加上M2”或者“M1和M2相加”来表示。这里是因为数量运算关系“M1+M2”和“M1*M2”它们本身存在着不同的整合层级。
吴为善提出:“概念整合理论认为,语言成分的整合依赖两个因素,一个是整个框架,另一个是输入元素,在框架的作用下,元素的某些语义特征被激活,元素之间的连通性被映射,并且产生整合效应,由此形成新创意义”[12]。张云秋和王馥芳指出“概念整合是存在层级的,如果两个概念在其基本义或本义基础上提取部分语义特征进行整合,这种整合是低层级整合;如果两个概念在其引申义基础上提取部分语义特征进行整合,这种整合是高层级整合”[13]。笔者认为“M1+ M2”这个格式在认知上是以“和”这个加法运算为框架,以“M1、M2”为输入元素,形成的低层级整合。而以乘法运算为框架,以“M1、M2”为输入元素形成的格式则是相对较高层级的整合。
整合层级的高低对应着概念整合网络的复杂程度。所谓的概念整合网络,是概念整合理论中,以某些框架为主要结构的心理空间网络。Fauconnier与Turner把这种心理网络分为四个空间(图1):输入空间Ⅰ(Input SpaceⅠ)、输入空间Ⅱ(Input SpaceⅡ)、类属空间(Generic Space)、合成空间 (Blending Space)。两个输入空间提供“框架”与“元素”,类属空间是建构在两个输入空间之上的抽象认知,也为合成空间提供输入,最后由合成空间利用已有的框架和元素,进行合成扩展,产生新的心理认知。
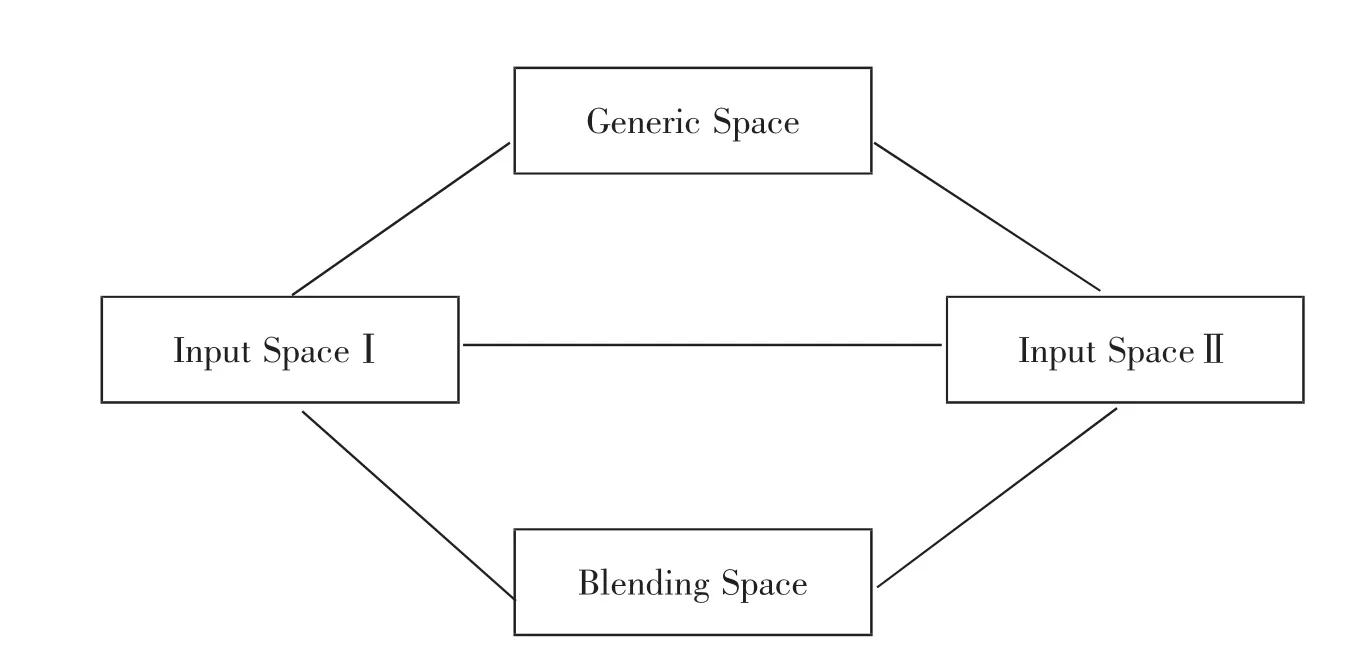
图1 概念整合网络
加法只是单一的整合了M1、M2这两个元素,而乘法的本质则是M2个M1的整合。乘法的本质是加法,但是在反复调用自身的基础上,实现复杂的整合(图2)。这也是为什么我们不说“整体大于部分之积”,而只是说“整体大于部分之和”,因为相乘是一种高整合层级的过程,蕴含着无数的可能性,很有可能是远远超过整体的。
另一方面,我们可以把并列结构与偏正结构做了一个简单的对比:
a1.妈妈和爸爸-爸爸和妈妈
a2.妈妈的爸爸-爸爸的妈妈
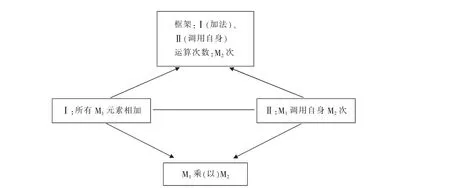
图2 “乘”概念整合网络
b1.小熊猫和杯子-杯子和小熊猫
b2.小熊猫的杯子-*杯子的小熊猫
c1.我们和学校-学校和我们
c2.我们的学校-学校的我们
从例子中可以看出,在调换了名词成分的位置之后,并列结构的语义基本不变,而偏正结构的语义则发生了巨大变化。可见,偏正结构与并列结构相比凝固性更强,内部凝固而产生特定的意义了,不能随意改变。因此我们可以看出,“M1+ M2”无法用偏正结构来表示,是因为其本身的整合层级没有达到偏正结构的要求,也就是 “M1+ M2”这种低整合度的结构没有办法用偏正结构这种高整合度的结构来表示,这也反证出了“M1*M2”之所以可以用“M1的M2倍”这种偏正结构来表示,并不是偶然,而是因为它们在扩充性与整合度之间存在着一定的对应关系(图3)。
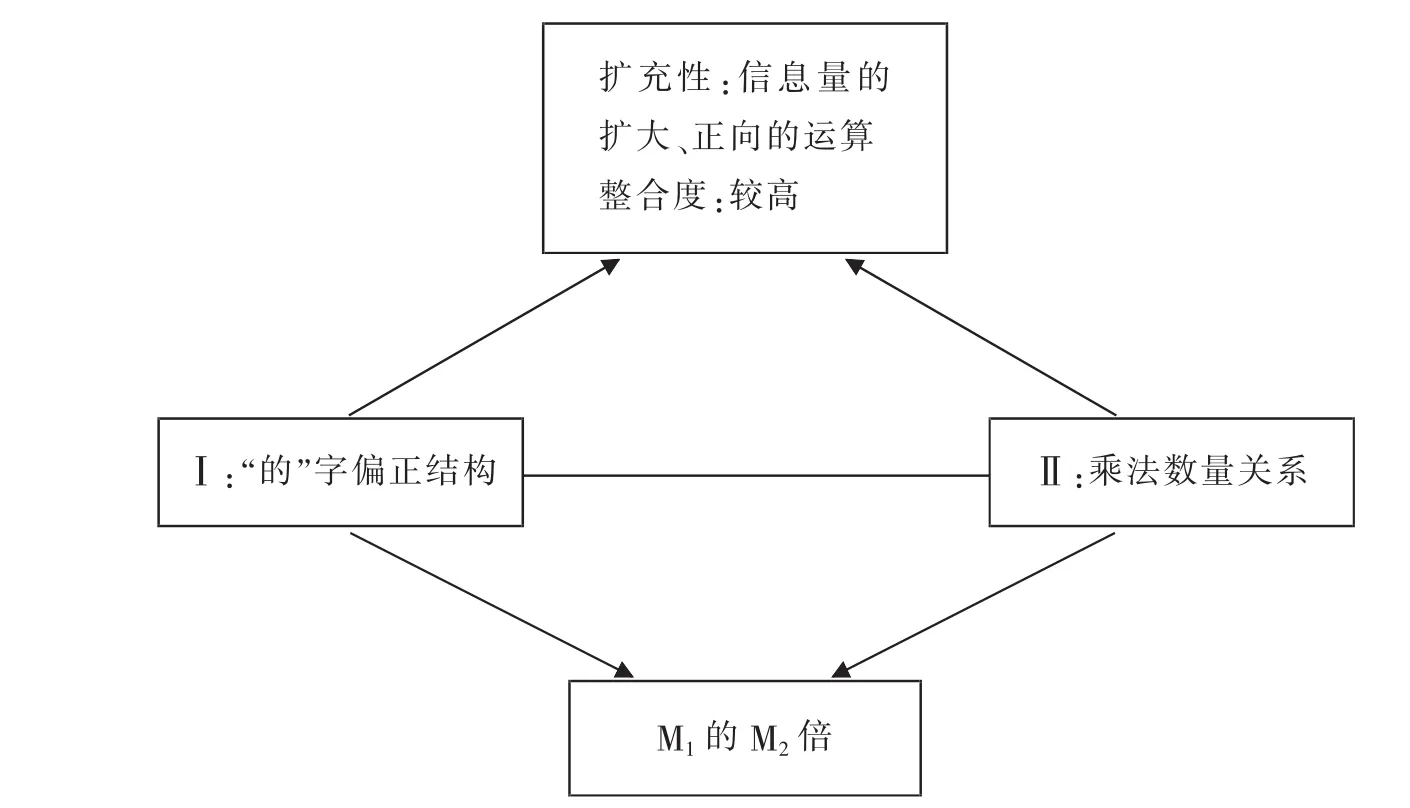
图3 “‘的’字结构”与“乘法数量关系”概念整合网络
3 总结
综上所述,本文首先对“M1的M2倍”格式进行了考察,发现这种以数量运算关系为核心的偏正结构存在着一定特殊性,而这种特殊性正是因为概念隐喻而产生。因此,通过分析偏正关系“M1的M2倍”与“M1*M2”这种抽象的数量运算关系之间的隐喻机制,包括其中整合网络的不同,总结出在偏正关系这个概念域去映射数量关系这个概念域时需要两个认知触动点,即扩充性与高整合度的双重达标,才能使隐喻发生。
参考文献:
[1]汉语大字典编辑委员会.汉语大字典:第二版[Z].成都:四川出版社,2010:183.
[2]朱德熙.语法讲义[M].北京:商务印书馆,1982:48.
[3]刘立.现代汉语量词研究[D].成都:四川师范大学,2010:21.
[4]齐沪扬.有关类固定短语的问题[J].修辞学习,2001,(1):8+2.
[5]布龙菲尔德.语言论[M].北京:外语教学与研究出版社,2002:226-238.
[6]LAKOFF G.Women,fire,and dangerous things[M].Chicago:The University of Chicago Press,1987:338-353.
[7]LAKOFF G,JOHNSON M.Metaphors we live by[M].Chicago:The University of Chicago Press,1980:127.
[8]王寅.什么是认知语言学[M].上海:上海外语教育出版社,2011:129-131.
[9]张敏.认知语言学与汉语名词短语[M].北京:中国社会科学出版社,2008:90-103.
[10]FAUCONNIER G.Mental spaces:aspects of meaning construction in natural language[M].Cambridge:Cambridge University Press,1994:59-72.
[11]沈家煊.“王冕死了父亲”的生成方式——兼说汉语“糅合”造句[J].中国语文,2006,(4):291-300+383.
[12]吴为善.汉语韵律框架及词语整合效应[M].上海:学林出版社,2011:35.
[13]张云秋,王馥芳.概念整合的层级性与动宾结构的熟语化[J].世界汉语教学,2003,(3):46-51+3.
A COGNITIVE ANALYSIS OF THE“M2TIMES OF M1”FORMAT
XIE Wen-jie
(Anhui University,Hefei Anhui 230000)
In the quantitative relationship of the format,“M2times of M1”,M means numerals,such as“three times of five”, “eleven times of eleven”and this kind of structure.Modifying construction of“de structure”is used to describe,however,the quantitative relation which is relative to or related to,and some construction can use it describe while others can not.Through the analysis of the form of“M2times of M1”,and using the concept of metaphors and integrated cognitive linguistics,this paper tries to explore the particularity of this partial structural expressions and at the same time tries to explore the hidden cognitive mechanism under the background by using the partial structure to express the quantitative relation.
“M2times of M1”;Modifying construction;Metaphor
H13
A
1672-2868(2017)02-0103-06
责任编辑:陈 凤
2016-12-29
谢文杰(1992-),男,安徽滁州人。安徽大学文学院,硕士研究生。研究方向:认知语言学与计算语言学。

