外圈故障滚动轴承周期运动Neimark-Sacker分岔研究

王 强，刘永葆，徐慧东，贺 星，刘树勇

（1.海军工程大学 动力工程学院，武汉430033；2.湖南大学 机载与运载工程学院，长沙 410082）

外圈故障滚动轴承周期运动Neimark-Sacker分岔研究

王 强1，刘永葆1，徐慧东2，贺 星1，刘树勇1

（1.海军工程大学 动力工程学院，武汉430033；2.湖南大学 机载与运载工程学院，长沙 410082）

文章基于非线性理论，建立了三自由度非光滑系统轴承外圈故障模型，研究了该情况下，系统周期运动的Neimark-Sacker分岔现象和混沌等非线性行为。求出系统的切换矩阵，将得到的切换矩阵结合Floquet理论确定了该非光滑系统周期运动发生Neimark-Sacker分岔的条件。通过在碰撞面处建立Poincaré映射，用数值方法进一步揭示轴承系统的周期运动经Neimark-Sacker分岔通向混沌的现象。发现当旋转频率接近临界分岔点时，系统有一对Floquet特征乘子的模接近1，其余特征乘子模都小于1，系统发生Neimark-Sacker分岔，随着旋转频率的增加，系统经历了典型的Neimark-Sacker分岔通向混沌的非线性行为。同时研究了不同的阻尼系数对系统分岔的影响，发现阻尼可以有效地延迟系统的分岔点。对该故障轴承系统分岔和混沌的研究，可为实际装备安全运行及故障诊断提供依据，同时为设计提供理论指导和技术支持。

轴承；Floquet理论；倍化分岔；混沌

0 引 言

随着船舶事业的大发展，燃气轮机作为舰船的主动力正在逐步地发展，而目前燃气轮机在运行过程中极易出现故障，几年前某船在海上航行过程中，出现了多级叶片损坏，轴承严重失效的故障，造成了重大损失。在燃机用来发电的设备使用中，国内外也出现了多起轴承损坏造成严重事故的情况。据统计轴承作为一个旋转核心部件发生故障的概率占所有设备故障的30%，因此，本文针对这种情况，从最根本的轴承碰撞出发，研究了轴承在运转过程中出现的分岔混沌等非线性振动行为，为设备的轴承设计、健康管理和预测诊断提供重要的理论依据。而碰撞问题属于强非线性、非光滑系统的一种，常用的线性化假设已经不能满足需要，必须考虑非线性、非光滑因素的的影响。在光滑的非线性领域已有了很多成熟的理论，Lyapunov、Bendix、Dulac和Birkoff等人讨论的系统的稳定性、极限环以及不变流形等问题，而Poincare、Andronov和Bogolubov等人的如小参数法、坐标变形法、多尺度法、慢变参数法、KBM法、谐波平衡法、等效线性化方法等来逼近非线性系统的精确解[1]。随着非线性理论的发展，出现了如混沌的结构和普适性、分岔、分形、突变、奇异性、奇怪吸引子、混纯同步等等[2-3]，形成了非线性动力学中的主要概念以及理论基础。而中心流行理论、分岔理论、奇异性理论、摄动理论等光滑系统的非线性理论在非光滑系统中，这些理论并不能完全适用或做很大修改，而且出现了许多常规光滑系统没有的特殊非线性现象，如角点碰撞、粘滞—滑移分岔、C—型奇怪吸引子等。

目前非线性理论在各个领域有了突破和应用。国外，Shaw和Holmes[4]对一类在简谐激振力作用下有单侧约束的单自由度振子做了研究，用中心流形定理分析了周期运动的局部分岔，并通过同宿相截条件讨论了混沌运动。Peterka[5]研究了具有粘滞阻尼的碰撞振子中的擦边分岔、周期倍化分岔和鞍结分岔之间的转迁现象。Kleczka等人[6]通过对不稳定周期解延续及胞映射方法发现并讨论了含间隙振子中混沌的激变现象。Leine等人[7]对非光滑系统周期解的不连续分岔作了进一步的研究，分析了伴随基解矩阵的跳跃而发生的各种不连续分岔现象。Luo[8]研究了一个分段线性周期激励系统，通过建立相应映射，研究了各类稳定和不稳定的周期运动。国内，在医学方面，陈方方，洪灵等人[9]根据一类具有时滞及非线性特性发生率的SIRS传染病模型，将非线性发生率的引入其中，运用中心流形定理和规范型理论进行研究分析，给出了分岔方向及分岔周期解稳定性的计算公式，利用特征值理论分析了模型的Neimark-Sacker分岔行为及平衡点的局部稳定性。夏小飞，王俊松[10]基于分岔理论，通过神经群模型兴奋性和抑制性突触增益的余维一分岔分析，分别给出了神经群运行于单稳、双稳、正常和异常极限环振荡状态的兴奋性和抑制性突触增益的单参数区间，进而通过兴奋性和抑制性突触增益的余维二分岔分析给出了神经群运行于上述多种状态的双参数区域。在电力系统方面，王晓东，陈予恕[11]运用多尺度法和C-L方法研究了单机无穷大电力系统在外部周期性负荷扰动作用下的解析解及其稳定性和主共振响应在不同系统参数下的不同分岔模式，发现了系统具有倍周期分岔、混沌、增幅振荡失步等丰富动力学行为，可为电力系统中同步发电机使用提供理论指导。陈章耀等人[12]研究了自治与非自治电路系统在周期切换连接下的动力学行为及机理，采用系统周期切换的方法分析了Rayleigh振子的不同参数下，两子系统的周期振荡行为，及切换系统随参数变化的最大李雅普诺夫指数及对应的分岔图，研究了其复杂的非线性行为及振荡机理。而研究最多的主要集中在非线性理论的研究和机械系统中存在各种非线性，郑小武，谢建华等人[13]采用Floquet-Lyapunov理论将常系数系统的控制分岔行为的方法应用于一类具有周期系数的力学微分系统，研究了其控制平衡点分岔行为的有效性，设计了相应的控制器，将的Flip分岔行为和Neimark-Sacker分岔行为最后控制在周期一点。侯东晓等人[14]应用多尺度法和奇异性理论分析一类具有三势阱Mathieu-Duffing振子系统在非自治情况下的余维三分岔特性，获得系统在Smale马蹄意义下混沌的阈值，研究了系统的混沌行为和安全盆分岔。王学弟等人[15]基于非线性动力系统的分岔控制理论，研究了一个新的非线性动力系统的Neimark-Sacker分岔极限环幅值的控制问题，对应本系统应用具体的非线性控制器实现了Neimark-Sacker分岔极限环幅值的反馈控制，时得到了计算极限环幅值近似值的计算公式。吴鸿涛，张艳龙[16]研究了在随机干扰条件下对两自由度碰撞振动系统倍化分岔的影响。柴林，吴晓明[17]建立了单自由度碰撞振动机械的通用动力学模型，研究了碰撞间隙、阻尼、刚度、激振频率等参数对系统运动出现的分岔和混沌现象的影响。于海，陈予恕[18]针对航空发动机低压转子系统，采用降维方法将26维裂纹故障的高维非线性动力学模型降为2自由度的含有特征的低维非线性系统，得到了各种不同的分岔模式，反映了裂纹转子的动力学特征。苟向锋等人[19]建立了三自由度单级直齿轮副传动系统的扭转振动非线性动力学模型，结合系统相图、Poincaré映射图及FFT频谱图，分析了系统在激励频率变化时的动力学特性。李晓贞，朱如鹏[20]基于集中参数理论，建立了正交面齿轮多自由度耦合振动模型，采用龙格库塔数值积分法对系统的动力学方程求解，得到随摩擦系统变换的系统动态响应分岔特性。而目前单独针对轴承本身的非光滑、非线性振动的研究还没有。

轴承作为旋转机械最核心的关键部件之一，轴承本身轻微异常振动反应在外围的旋转机械部件会有一个放大，尤其在高速旋转的情况下，可能造成意想不到的后果，如燃机轮机等叶片的碰磨，振动破坏，机械设备的损坏，甚至造成人员的伤亡。轴承一旦发生破损等故障时会造成更严重的后果，因此本文针对轴承本身，建立轴承三自由度故障模型，研究轴承非光滑、非线性振动行为。

1 故障滚动轴承建模分析及运动过程

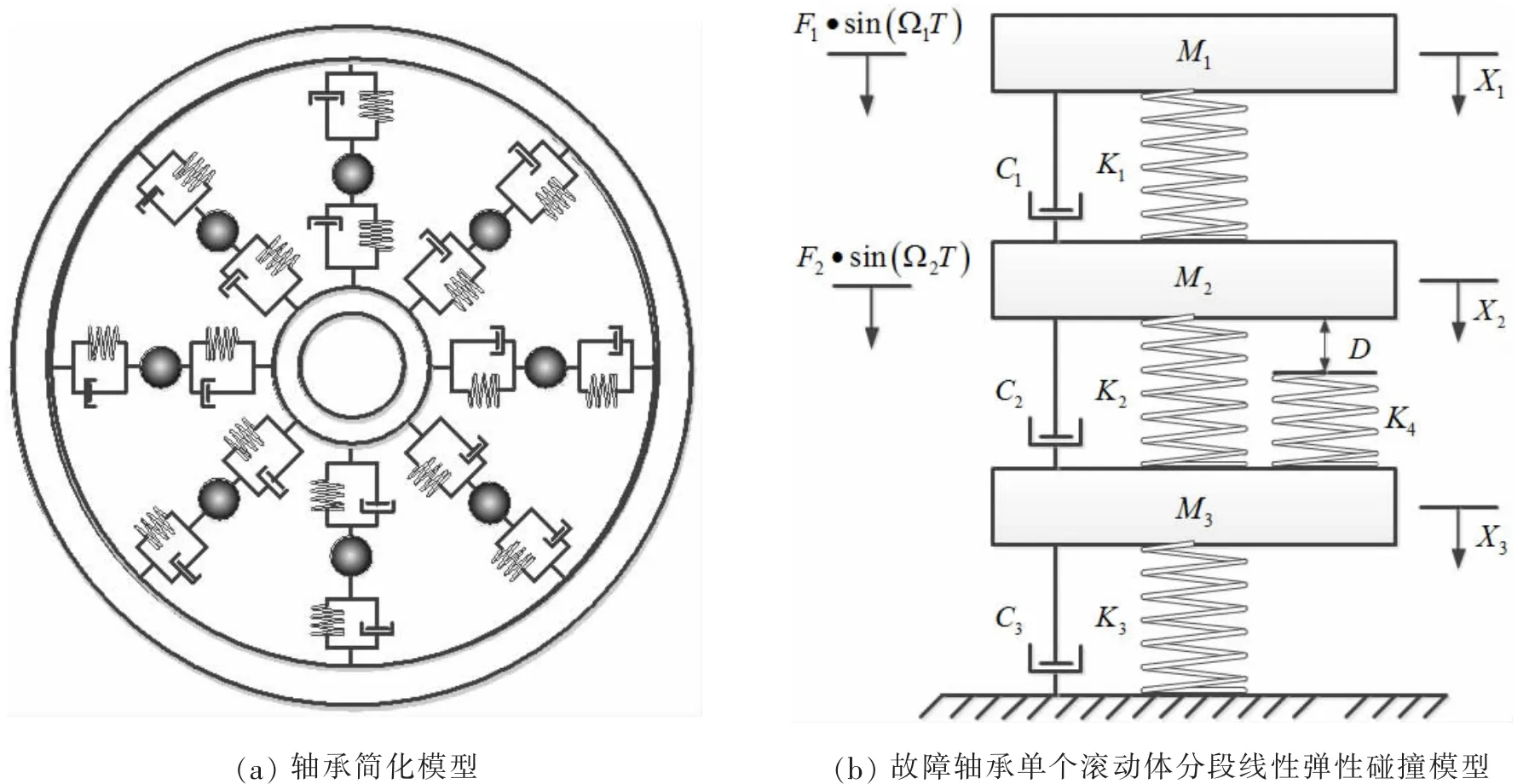
图1 滚动轴承简化模型Fig.1 The simplified rolling bearing model

根据轴承的滚动模型图1（a）建立外圈存在故障的情况下轴承单个滚动体的简化模型如图1（b）所示。M1，M2，M3分别为内圈与轴的等效质量、滚动体质量、外圈及机座的质量，X1，X2，X3分别为M1，M2，M3的运动的位移；C1，C2，C3别为M1与M2的阻尼，M2与M3之间阻尼，M3与固定端阻尼，K1，K2，K3分别为三个物体之间的刚度，K4为发生故障时，外圈与滚动体之间的接触刚度。F1sin（ Ω1T），F2sin（ Ω2T ）分别为作用在M1，M2的等效作用力，D为故障深度，Ω1与Ω2分别为转轴和保持架的频率，发生故障时Ω1与Ω2的关系为：

图2 轴承模型二维相平面图Fig.2 The two-dimensional phase plane of bearing model

内圈转动频率为fr=N/60（N为转轴转速）；外圈转动频率fo=0；滚动体个数为Nb；接触角为α；轴承节圆直径；滚动体直径d；外圈半径R，内圈半径r，Ω1=fr，Ω2=fr/Nb。

为了描述该轴承系统的运动过程，引入一个分界面。首先定义边界函数，E=X2-X3-D，分界面可表示如下：

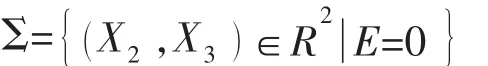
表示物块M2与M3刚接触或分离，这样状态空间被分界面分成两部分，如图2所示。

根据上面的分析，可建立系统的运动学方程如下：

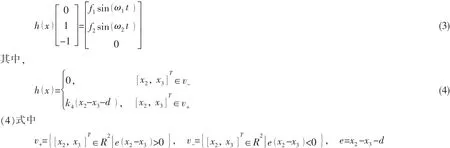
2 系统周期运动的Floquet特征乘子分析

将系统（3）和（4）写为如下的规范式：

设系统（5）的一个解x（t）从区域v-出发，即x（ t0）∈v-。在t=tp时刻到达分界面Σ。系统在区间是连续的，相应的基解矩阵也是连续的。然而由于向量场f（ t， x（t））在分界面处的非光滑性使得相应的Jacobian矩阵在分界面处通常是不连续的，这将引起系统整个基解矩阵不连续，因此在不连续处需要求出相应的切换矩阵。

下面来求分界面处的切换矩阵。

（1）从区域v-进入区域v+时，对超平面Σ：e=x2-x3-d=0，有法向量n=［0，0，1，0，-1，0 ］T，设一周期解x（t）到达分界面Σ的时间为t1并交于点。在t1时刻计算切换矩阵如下

（2）从区域v+进入区域v-，设周期解x（t）到达分界面Σ的时间为t2并交于点，在时刻t2有切换矩阵

下面求各光滑区域的基解矩阵。在区域v-系统的运动方程为

因为我们研究的是系统（5）穿越了分界面的周期解，将切换矩阵（8）和（9）结合各子空间相应的基解矩阵（13）和（14）经过合成可得全局的单值矩阵：

（16）式中，T=2nπ/ω1为系统周期的整数倍，n为自然数；t0表示初始时刻，t1和t2分别表示轨线到达分界面的两段时间。

于是系统的Floquet特征乘子即为单值矩阵（16）的特征值。对于系统（5）这样的非光滑系统，由于分界面是光滑的，系统的Floquet特征乘子是连续穿越单位圆周的。当一对Floquet特征乘子的模等于1，其它特征乘子仍位于单位圆内时，系统（5）稳定的周期解将发生Neimark-Sacker分岔。

3 数值分析

为了通过数值仿真进一步揭示滚动轴承系统（3）和（4）的倍化分岔通向混沌的现象，在分界面Σ处取Poincare截面如下：

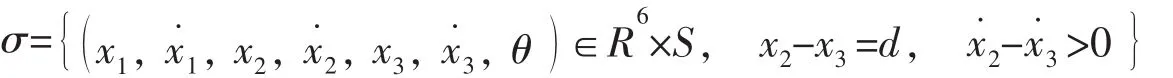
其中：θ=ω1t；S=R（ mod 2π）为1个实数对2π取余数。

选取系统（3）和（4）的一组无量纲化参数：

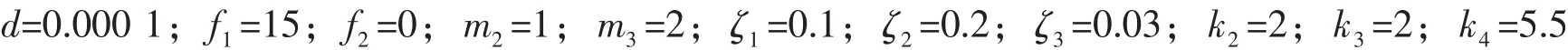
以旋转频率ω1为分岔参数。

当ω1=2.831时（ωs为轴承临界分岔的旋转频率），轴承故障系统对应的其中一对Floquet特征乘子为，接近单位圆周上的（1，0）点，其余特征值的模都小于1，位于单位圆内，所有的特征值为：

由此可见轴承外圈故障系统在ω1=2.831时发生了Neimark-Sacker分岔。系统随ω1变化的分岔图如图3所示。系统起初处于稳定的单周期运动，如ω1=2.75时图4所示的相图和庞相莱截面图。当ω1=2.95时，系统经过了分岔点ω1=2.831发生了Neimark-Sacker分岔，如图5所示的相图和庞加莱截面图。研究了当外圈m3发生Neimark-Sacker分岔时内圈m1和滚动体m2的振动行为，其运动行为的庞相莱截面图如图6所示。同时研究了碰撞面处不同的阻尼系数对系统分岔点及相图和庞相莱截面的影响，可以明显看出，阻尼系数增加对系统的振动有很大的衰减作用，随着阻尼系数的增大，系统的分岔点会逐渐增大甚至消失如表1所示。

表1 不同的阻尼系数ζ3对系统分岔的影响Tab.1 The influence of different damping coefficients ζ3on the bifurcation of system

图3 系统的分岔图Fig.3 The bifurcation diagram of the system

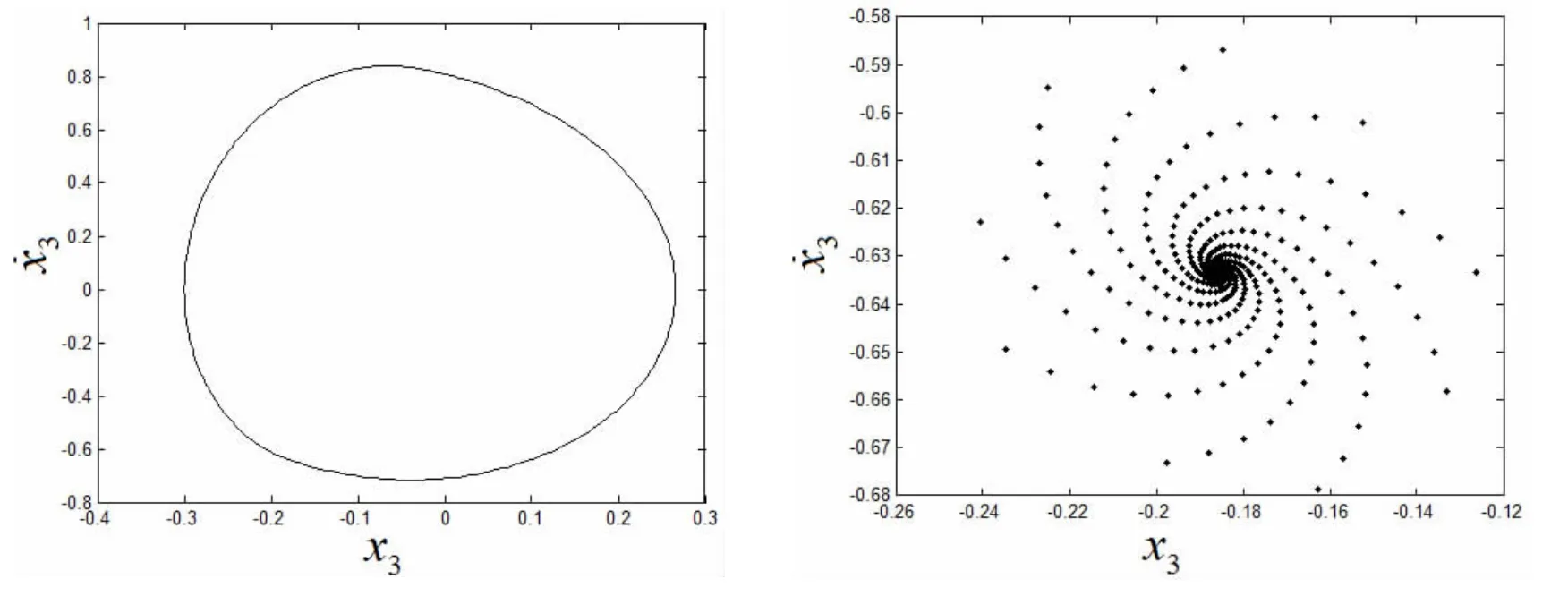
图4 ω1=2.75时单周期运动的相图和庞加莱截面图Fig.4 The phase diagram and poincare section diagram of single periodic motion at ω1=2.75

图5 ω1=2.95时运动的相图和庞加莱截面图Fig.5 The phase diagram and poincare section diagram at ω1=2.95

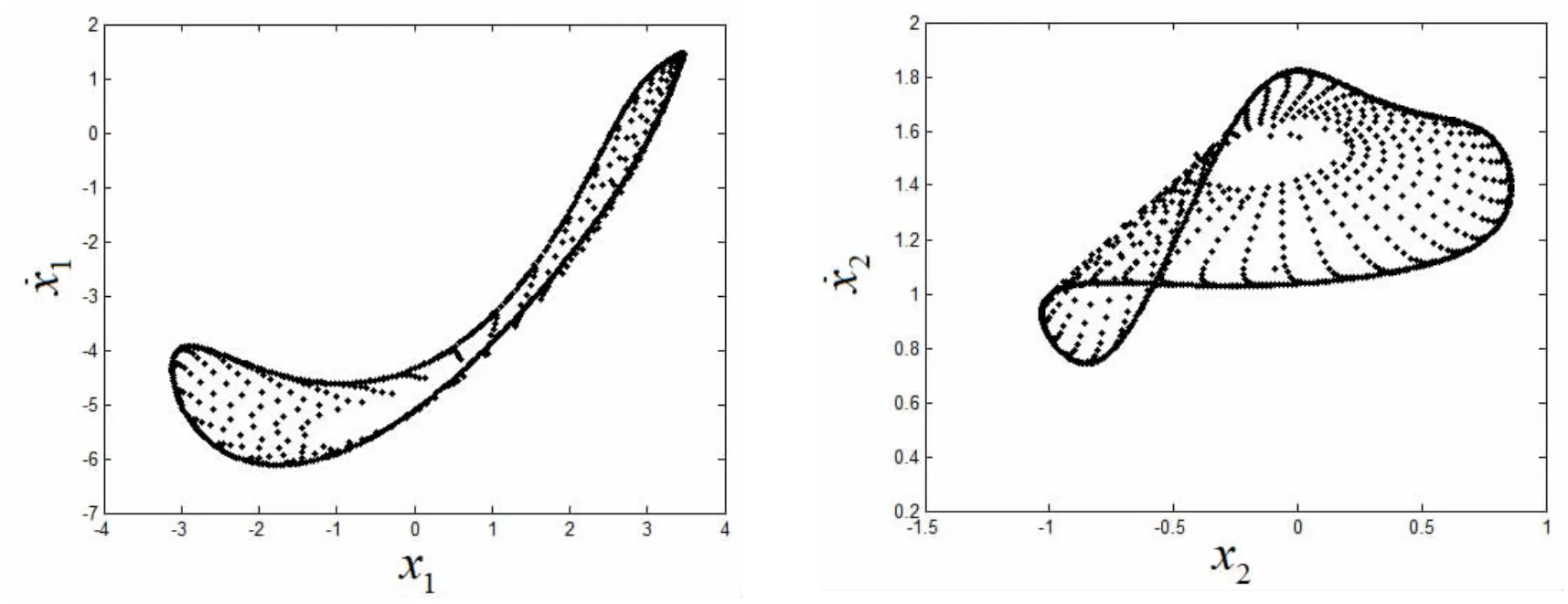
图6 ω1=2.95时内圈m1和滚动体m2的庞加莱截面图Fig.6 The poincare section diagrams of inner ring m1and cage ball m2at ω1=2.95

当选取系统（3）和（4）的无量纲化参数：

d=0.000 1；f1=15；f2=0；m2=1；m3=2；ζ1=0.1；ζ2=0.2；k4=5.5；k2=2；k3=2；基本参数保持不变，当ζ3减小到ζ3=0.02时，以旋转频率ω1为分岔参数，依据Floquet理论及前面的公式推导，确定此时系统的分岔点。

当ω1=2.772 4时（ωs为轴承临界分岔的旋转频率），轴承故障系统对应的其中一对Floquet特征乘子为，接近单位圆周上的（1，0）点，其余特征值的模都小于1，位于单位圆内，所有的特征值为：

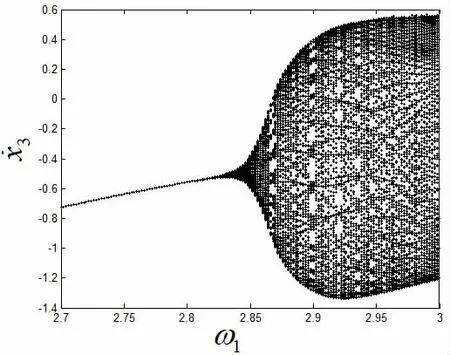
图7 系统的分岔图ζ3=0.02Fig.7 The bifurcation diagram of the system ζ3=0.02

由此可见轴承内圈故障系统在ω1=2.772 4时发生了Neimark-Sacker分岔。系统随ω1变化的分岔图如图7所示。

图8 ω1=2.75时运动的相图和庞加莱截面图Fig.8 The phase diagram and poincare section diagram at ω1=2.75

图9 ω1=2.9时运动的相图和庞加莱截面图Fig.9 The phase diagram and poincare section diagram at ω1=2.9

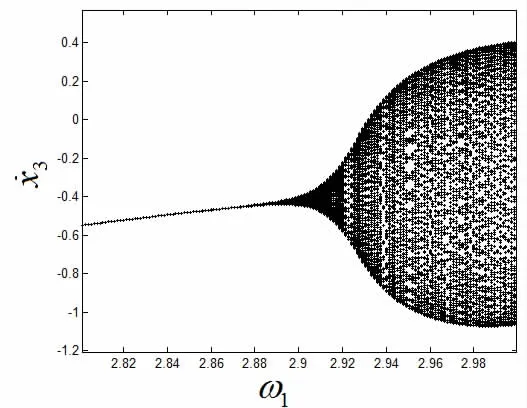
图10 系统的分岔图ζ3=0.04Fig.10 The bifurcation diagram of the system ζ3=0.04

同时选取系统（3）和（4）的无量纲化参数，基本参数保持不变，当ζ3增大到ζ3=0.04时，以旋转频率ω1为分岔参数，依据Floquet理论及前面的公式推导，确定此时系统的分岔点。

当ω1=2.879时（ωs为轴承临界分岔的旋转频率），轴承故障系统对应的其中一对 Floquet特征乘子为，接近单位圆周上的（1，0）点，其余特征值的模都小于1，位于单位圆内，该所有的特征值为：

图11 ω1=2.85时运动的相图和庞加莱截面图Fig.11 The phase diagram and poincare section diagram at ω1=2.85

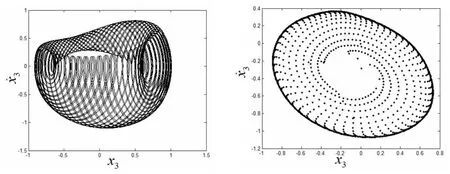
图12 ω1=2.98时运动的相图和庞加莱截面图Fig.12 The phase diagram and poincare section diagram at ω1=2.98

由此可见轴承内圈故障系统在ω1= 2.879时时发生了Neimark-Sacker分岔。系统随ω1变化的分岔图如图10所示。

同时选取系统（3）和（4）的无量纲化参数，基本参数保持不变，当ζ3增大到ζ3=0.1时，系统的分岔图如图13所示。

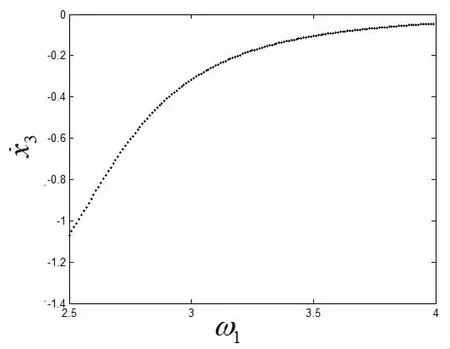
图13 系统的分岔图ζ3=0.1Fig.13 The bifurcation diagram of the system ζ3=0.1

4 结 论

本文针对轴承内圈破损故障，建立了轴承三自由度分段非光滑模型，应用F-loquet理论分析了该系统周期运动发生倍化分岔的条件。结果表明系统有1对Floquet特征乘子的模接近1，其余特征乘子的模小于1，系统发生了Neimark-Sacker分岔，数值仿真进一步调查了系统由单周期经过分岔点通向Neimark-Sacker分岔的过程；研究了当外圈发生Neimark-Sacker分岔时对内圈和滚动体的影响发生了类似Neimark-Sacker分岔行为；同时通过研究不同的阻尼系数对系统分岔的影响，发现阻尼可以有效地延长系统的分岔点，减少系统的分岔混沌等非线性行为。

致谢

非常感谢国家自然科学基金资助项目（51179197），国家海洋工程重点实验室（上海交通大学）基金资助项目（1009）。

[1]周纪卿,朱因远.非线性振动[M].西安:西安交通大学出版社,1997.

[2]Golubitsky,Schaeffer.Singularities and groups in bifurcation theory[M].Springer-Verlag,New York,1985.

[3]Kurths J,mayer-Kress.Nonlinear analysis of physiological data[M].Springer-Verlag,Berlin,1998.

[4]Shaw S W,Holmes P J.A periodically forced piecewise linear oscillator[J].Journal of Sound and Vibration,1983,90(1): 129-155.

[5]Peterka E.Bifurcation and transition phenomena in an impact oscillator[J].Chaos,Solitons and Fractals,1996,7(10): 1635-1647.

[6]Kleczka M,et a1.Nonlinear dynamics in engineering systems[M].Ed.By Schiehlen,Springer-Verlag,1990:141-148.

[7]Leine R I,Nijmeijer H.Dynamics and bifurcation of non-smooth mechanical systems[M].Berlin,Springer,2004:101-118.

[8]Luo A C J,Che L.Periodic motions and grazing in a harmonically forced,piecewise,linear oscillator with impacts[J]. Chaos,Solitons and Fractals,2005,24:567-578.

[9]陈方方,洪 灵.一类具有时滞和非线性发生率的SIRS传染病模型稳定性与Neimark-Sacker分岔分析[J].动力学与控制学报,2014,12(1):79-85. Chen Fangfang,Hong Ling.Stability and neimark-sacker bifurcation analysis of a delayed sirs epidemic model with nonlinear saturation incidence[J].Journal of Dynamic and Control,2014,12(1):79-85.

[10]夏小飞,王俊松.基于分岔理论的突触可塑性对神经群动力学特性调控规律研究[J].物理学报,2014,63(14): 140503-1:10. Xia Xiaofei,Wang Junsong.Influence of synaptic plasticity on dynamics of neural mass model:A bifurcation study[J]. Acta Phys.Sin.2014,63(14):140503-1:10.

[11]王晓东,陈予恕.一类电力系统的分岔和奇异性分析[J].振动与冲击,2014,33(4):1-6. Wang Xiaodong,Chen Yushu.Bifurcation and singularity analysis for a class of power systems[J].Journal of Vibration and Shock,2014,33(4):1-6.

[12]陈章耀,雪增红,张 春,季 颖,毕勤胜.周期切换下Rayleigh振子的振荡行为及机理[J]物理学报,2014,63(1): 010504-1:8. Chen Zhangyao,Xue Zenghong,Zhang Chun,Ji Ying,Bi Qinsheng.Oscillation behaviors and mechanism of Rayleigh oscillator with periodic switches[J].Acta Phys.Sin,2014,63(1):010504-1:8.

[13]郑小武,谢建华.一类周期系数力学系统分岔控制[J].西南交通大学学报,2014,49(4):741-745. Zheng Xiaowu,Xie Jianhua.Bifurcation control of mechanical system with periodic coefficients[J].Journal of Southwest Jiaotong University,2014,49(4):741-745.

[14]刘 彬,赵红旭,侯东晓.一类含三势阱Mathieu-Duffing振子的相对转动系统的分岔和混沌[J].物理学报,2014,63 (17):174502-1:9. Liu Bin,Zhao Hongxu,Hou Dongxiao.Bifurcation and chaos of some relative rotation system with triple-well Mathieu-Duffing oscillator[J].Acta Phys.Sin.,2014,63(17):174502-1:9.

[15]王学弟,彭 淼,杨天宇.一个新系统Neimark-Sacker分岔极限环幅值控制[J].工程数学学报,2014,31(4):557-566. Wang Xuedi,Peng Miao,Yang Tianyu.Amplitude control of limit cycle from neimark-sacker bifurcation of a new system [J].Chinese Journal of Engineering Mathematics,2014,31(4):557-566.

[16]吴鸿涛,张艳龙.随机干扰对两自由度碰撞振动系统的倍化分岔的影响[J].兰州交通大学学报,2014,33(3):59-63. Wu Hongtao,Zhang Yanlong.The effect of stochastic disturbance on doubling bifurcation of a TWO-DOF Vibro-impact system[J].Journal of Lanzhou Jiaotong University,2014,33(3):59-63.

[17]柴 林,吴晓明.机械碰撞振动系统分岔与混沌的参数演化[J].厦门大学学报(自然科学版),2014,53(4):508-513. Chai Lin,Wu Xiaoming.Evolution of bifurcation and chaos in mechanical vibro-impact system with parameters[J].Journal of Xiamen University(Natural Science),2014,53(4):508-513.

[18]于 海,陈予恕,曹庆杰.多自由度裂纹转子系统非线性动力学特性分析[J].振动与冲击,2014,33(7):92-98. Yu Hai,Chen Yushu.Cao Qingjie.Nonlinear dynamic behavior analysis for a cracked multi-DOF rotor system[J].Journal of Vibration and Shock,2014,33(7):92-98.

[19]苟向锋,吕小红,陈代林.单级齿轮传动系统的Hopf分岔与混沌研究[J].中国机械工程,2014,25(5):679-683,691. Gou Xiangfeng,Lu Xiaohong,Chen Dailin.Research on Neimark-Sacker Bifurcation and chaos of the single-stage gear transmission system[J].China Mechanical Engineering,2014,25(5):679-683,691.

[20]李晓贞,朱如鹏,李政民卿,靳广虎.齿面摩擦对面齿轮传动系统振动特性的影响分析[J].振动工程学报,2014,27 (4):583-588. Li Xiaozhen,Zhu Rupeng,Li Zhengminqing,Jin Guanghu.Influences of frictional coefficient on vibration characteristic of face-gear transmission system[J].Journal of Vibration Engineering,2014,27(4):583-588.

Neimark-Sacker bifurcation of rolling bearing system with fault in outer ring

WANG Qiang1,LIU Yong-bao1,XU Hui-dong2,HE Xing1,LIU Shu-yong1
(1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China;2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha 410082,China)

Piecewise non-smooth model of three-degree-of-freedom rolling bearing system with fault in outer ring is established by the method of the nonlinear theory.The bifurcations and chaos of bearing system are studied.The switching matrixes of system are obtained at the switching boundaries,and the Neim-ark-Sacker bifurcation of non-smooth bearing system is analyzed by combining the switching matrixes with the Floquet theory for smooth systems.The numerical method is used to further reveal the bifurcations and chaos of bearing system through estabilshing the Poincare mapping on the collision plane.Results show that when the rotating frequency is decreased to a critical bifurcation point,a pair of complex conjugate Floquet multipliers is on the unit circle and others into a unit circle,and the Neimark-Sacker bifurcation appears.With the increase of rotating frequency,the system has experienced the nonlinear dynamical behaviors of classical Neimark-Sacker bifurcations to chaos.Also the influence of different damping coefficients on the bifurcation of system is analyzed and it is found that the damping of system can effectivelyreduce the nonlinear behaviors of bifurcation and chaos.The study of bifurcation and chaos of the fault bearing system provides reliable basis for the design and fault diagnosis and provides theoretical guidance and technical support for the actual design in the safe and stable operation of large high-speed rotating machinery.

bearing;floquet theory;period-doubling bifurcation;chaos

TH212 TH213.3

：Adoi:10.3969/j.issn.1007-7294.2017.05.013

1007-7294（2017）05-0621-12

2016-09-11

国家自然科学基金资助项目（51179197）；国家海洋工程重点实验室（上海交通大学）基金资助项目（1009）

王 强（1985-），男，博士研究生，E-mail：wangqiang13000306@163.com。