关于不定方程x(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3)

张 配 罗 明

(西南大学数学与统计学院， 重庆 400715)



关于不定方程x(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3)

张 配 罗 明

(西南大学数学与统计学院， 重庆 400715)

运用递推序列的方法，证明了不定方程x(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3)仅有正整数解(x,y)=(12,4)。

不定方程； 正整数解； 递归数列；Jacobi符号

不定方程是指未知数的个数多于方程个数，且未知数受到某些限制(如要求是有理数、整数或正整数等等)的方程。不定方程又称为丢番图方程,是数论的重要分支学科。不定方程大多数是由某些实际问题产生出来的，是反映现实世界数量关系的重要数学模型。

当(m,n)=1，且m,n∈N+时，对于形如

mx(x+1)(x+2)(x+3)=

ny(y+1)(y+2)(y+3)

的不定方程已有不少的研究[1-6]。

为此，在前人研究的基础上，利用同余式和递归数列方法证明当(m,n)=(1,39)时，不定方程

x(x+1)(x+2)(x+3)=

39y(y+1)(y+2)(y+3)

(1)

仅有正整数解(x,y)=(12,4)。

将方程(1)整理后得：

(x2+3x+1)2-39(y2+3y+1)2=-38

(2)

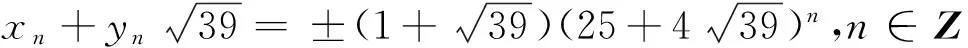
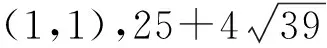
(2y+3)2=±4yn+5

(3)

或

(4)

容易验证式(5) — (11)成立：

un+1=50un-un-1,u0=1,u1=25

(5)

vn+1=50vn-vn-1,v0=0,v1=4

(6)

yn+1=50yn-yn-1,y0=1,y1=29

(7)

u2n= 2un2-1,v2n= 2unvn

(8)

yn=un+4vn

(9)

un+2h≡-un(moduh),vn+2h≡-vn(moduh)

(10)

yn+2h≡-yn(moduh)

(11)

下面证明式(3)仅当n=0,-1时成立。由此求得方程(2)的全部整数解，进而作为推论得到方程(1)的全部正整数解。将式(3)写成2个等式，其中一个为：

(2y+3)2=-4yn+5

(12)

引理1 -4yn+5是平方数仅对n=0成立。

证明 因为当|n|≥1时，-4yn+5<0，所以-4yn+5不可能是平方数；当n=0时，有-4yn+5=12。

式(3)写成另一个等式为：

(2y+3)2=4yn+5

(13)

引理2 设2|m,m>0，则

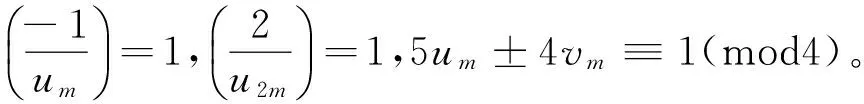
于是

引理3 若4yn+5为平方数，则必须有n≡0,1(mod180)。

证明 采用对序列4yn+5取模的方法来证明。

mod2 549，排除n≡2(mod5)，此时4yn+5≡703(mod2 549)。

上面的2 549是对{4yn+5}取的，mod5指出所得剩余序列周期为5。“此时”这句话是“排除”的理由：703为mod2 549的平方非剩余。为节省篇幅，只给出每次取模所用的素数以及n的剩余情况：

mod29，剩余n=0,1,6,11,13(mod15)。

mod210 869，剩余n=0,1,11(mod15)。

mod61，剩余n=0,1,15(mod30)。

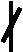
故得n=0,1(mod30)。

mod7，剩余n=0,1,3,4(mod6)。

mod19，剩余n=0,1,6,9,13(mod18)。

mod71，剩余n=0,1,6,9,27,36,60(mod72)。

mod1 249，排除n=6(mod8)，因此排除n=

6(mod72)。

mod41 617，排除n=6(mod9)，因此排除n=60(mod72)。

mod227，排除n=3,9(mod12)，因此排除n=9,27(mod72)。剩余n=0,1,36(mod72)，即剩余n=0,1(mod36)。

综合即剩余n=0,1(mod180)。

引理4 设n≡0(mod180)，则仅当n=0时，4yn+5是平方数。

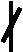
Ⅰ)k≡1(mod4)。令

则k≡1(mod4)情况下的数据见表1。

表1 k≡1(mod4)情况下的数据

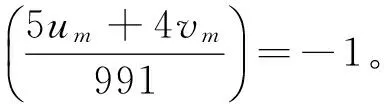
于是,由式(5)、(11)及引理1,有

4yn+5≡4y2m+5≡4v2m+5(modu2m)

得

从而4yn+5为非平方数。

Ⅱ)k≡-1(mod4)。令

则un≡1(mod5)情况下的数据见表2。

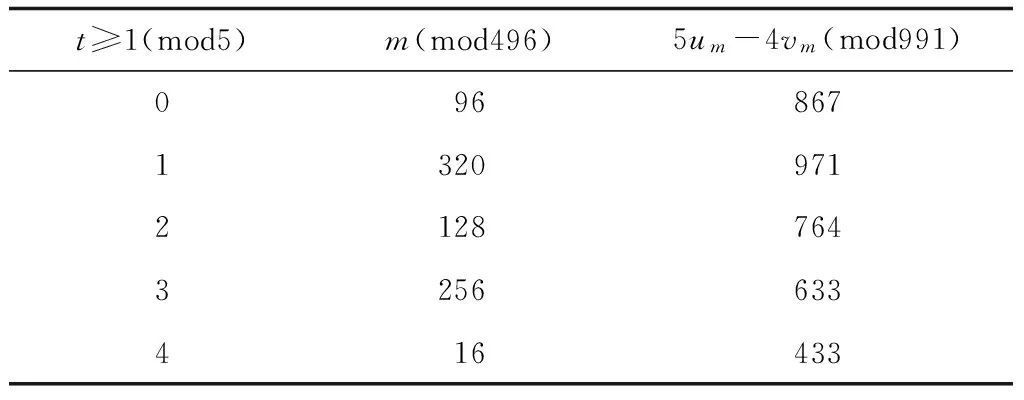
表2 un≡1(mod5)情况下的数据

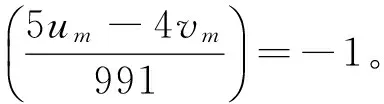
于是,由式(5)、(11)及引理1,有

4yn+5≡-4y2m+5≡-4v2m+5(modu2m)

得

从而4yn+5为非平方数。

引理5 设n≡1(mod180)，则仅当n=1时，4yn+5是平方数。

当t≡1,2,4(mod5)时，令m=2t；当t≡0(mod5)时，令m=3·2t；当t≡3(mod5)时，令m=9·2t；由式(11)，4yn+5≡-4y1+5≡-111(modum)，由于2|m时

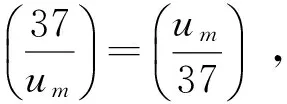
从而当n=0时，4yn+5=32，证毕。

3 结 果

根据上述讨论，现给出下列不定方程解的证明过程。

定理 不定方程x(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3)仅有一组正整数解(x,y)=(12,4)。

证明 由引理1有(2y+3)2=-4y0+5=1，因此y=-1,-2。

由引理4有(2y+3)2=4y0+5=9，因此y=0,-3。

由引理6有(2y+3)2=4y1+5=121，因此y=4,-7。

所以方程(1)共有20组整数解，其中有16组平凡解使其两端都为零，即(0,0),(0,-1),(0,-2),(0,-3),(-1,0),(-1,-1),(-1,-2),(-1,-3),(-2,0),(-2,-1),(-2,-2),(-2,-3),(-3,0),(-3,-1),(-3,-2),(-3,-3)。另外4组非平凡解，它们分别是(12,4),(-15,4),(12,-7),(-15,-7)。

因此，(x,y)=(12,4)是不定方程x(x+1)· (x+2)(x+3)=39y(y+1)(y+2)(y+3)仅有的一组正整数解，证毕。

对于此类不定方程，我们相当于求解某个代数簇上的有理点或整点。这样，一个数论问题就转化为某种几何问题。这种观点将数论与代数几何联系起来，是一种重要的数学思想。然而，对于代数曲线来说，相应的不定方程是否有解以及是否有无限个解，都与曲线的亏格密切相关。这就是著名的莫代尔猜想(由法尔廷斯证明)所包含的内容。亏格零的曲线就是直线和二次曲线，这就对应了上述的一次和二次不定方程。它将数论、复分析、代数几何、表示论等等都联系起来，是当代数学领域最重要的研究对象之一。

[1]COHNJHE.TheDiophantineEquationx(x+1)(x+2)·(x+3)=2y(y+1)(y+2)(y+3)[J].Pacific J Math,1971,37:331-335.

[2] PONNUDURAI T. The Diophantine Equationx(x+1)·(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].J London Math Soc,1975,10(2):232-240.

[3] 宣体佐.关于不定方程x(x+1)(x+2)(x+3)=5y(y+1)(y+2)(y+3)[J].北京师范学院学报(自然科学版)，1982(3)：27-34.

[4] 罗明.关于不定方程x(x+1)(x+2)(x+3)=7y(y+1)(y+2)(y+3)[J].重庆师范学院学报(自然科学版)，1991,8(1)：1-8.

[5] 程瑶，马玉林.关于不定方程x(x+1)(x+2)(x+3)=11y(y+1)(y+2)(y+3)[J].重庆师范大学学报(自然科学版),2007,7(1)：27-30.

[6] 罗明，郭凤明.关于不定方程x(x+1)(x+2)(x+3)=10y(y+1)(y+2)(y+3)[J].西南师范大学学报(自然科学版)，2013,38(10)：13-16.

[5] 张洪.关于不定方程x(x+1)(x+2)(x+3)=Dy(y+1)(y+2)(y+3)(D=21,23)[J].重庆工商大学学报(自然科学版)，2015,32(7)：56-61.

[7] 柯召，孙琦.谈谈不定方程[M].哈尔滨：哈尔滨工业大学出版社，2011：15-29.

On the Diophantine Equation:x(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3)

ZHANGPeiLUOMing

(School of Mathematics and Statistics, Southwest University, Chongqing 400715, China)

In this paper, with the method of recurrence sequences, we have shown that the diophantine equationx(x+1)(x+2)(x+3)=39y(y+1)(y+2)(y+3) has the only positive integer solution: (x,y)=(12,4).

diophantine equation; integer solution; recurrence sequence; Jacobi symbol

2016-10-27

国家自然科学基金项目(11471265)

张配(1990 — )，女，西南大学数学与统计学院在读硕士研究生，研究方向为代数数论。

O

A

1673-1980(2017)03-0120-03