无线传感网络中的神经网络多级数据融合算法

雷宇飞

(泉州信息工程学院， 福建 泉州 362000)



无线传感网络中的神经网络多级数据融合算法

雷宇飞

(泉州信息工程学院， 福建 泉州 362000)

根据传感器网络数据间的相关特性，基于神经网络的多级融合算法，利用数据间的时间-空间相关特性对采样数据进行二级融合处理，获得更准确的数据。仿真实验表明，本算法满足大数据环境下对数据精确度的要求。

感知节点； 神经网络； 置信度； 容错性

0 引 言

物联网技术是当今国际上备受关注的、由多学科高度交叉形成的新兴的前沿研究热点领域，具有全面感知、可靠传输、智能处理的特点，能够实时、可靠地获取目标区域各种监测对象的信息，在军事和民用中具有广泛的应用前景[1-2]。WSN是物联网技术中的核心技术之一，WSN具有自组织、自恢复、自适应的特点，通过各类集成化的微型终端节点协作完成信息采集任务，是当代物联网技术的核心环节和关键技术之一,在十大关键技术中荣居榜首[3]。

在WSN中，由于终端节点具有密度高的特点，而且节点之间具有自组织性能，因此,采集的数据具有时间-空间相关性，同一个数据在终端设备的传送过程中，节点存储的数据容易形成多个相同数据副本，造成存储资源浪费，形成大量不必要的冗余数据，容易造成数据传输过程中数据阻塞，降低传感器的网络实时性。另外，终端节点一般利用随机分布的方式自主组网，容易受到外界环境干扰，导致采样数据出现偏差、异常，甚至数据丢失的情况，给后续处理带来额外的开销。综上问题会导致WSN性能下降，影响物联网技术的实时性与准确性，而数据融合技术能够有效解决上述问题，是WSN技术中的关键技术之一[4]。

数据融合技术利用终端节点的数据和一定算法完成对同类数据的聚合处理，获得更少的数据量和更精确的数据值，一般原理结构如图1所示[5]。

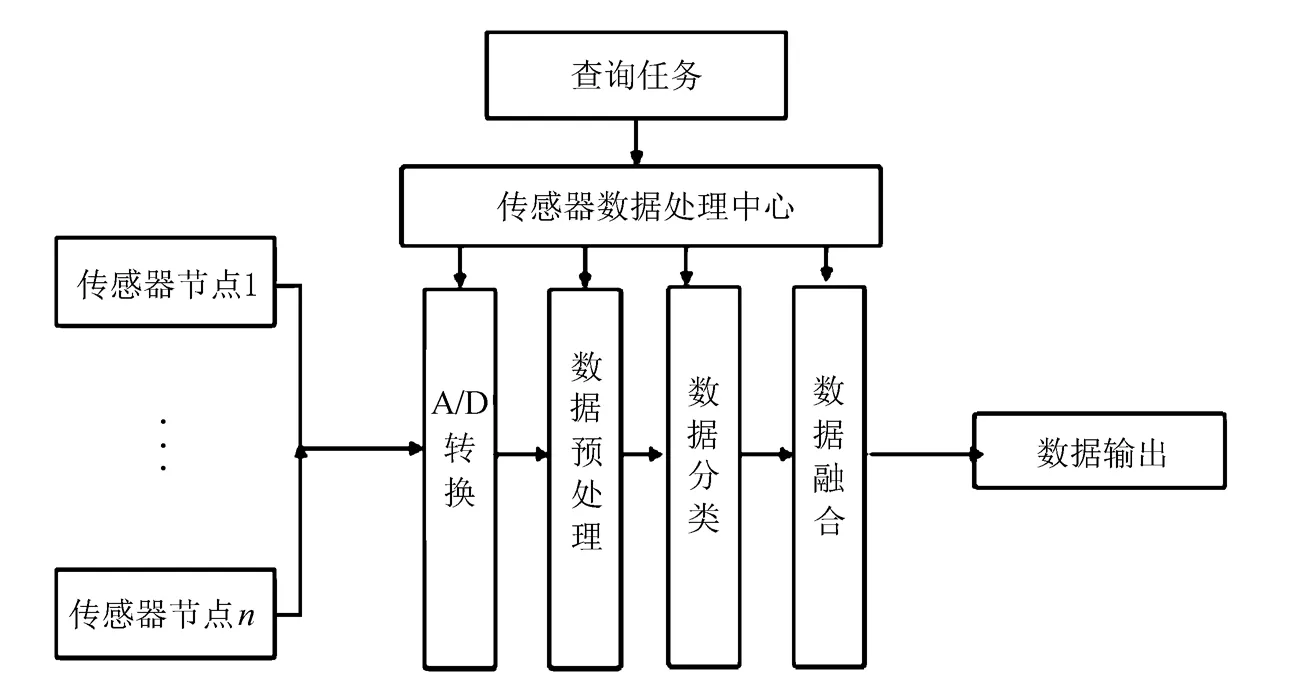
图1 数据融合的流程图

利用数据融合可以有效减少数据传输量。降低数据冲突，减轻网络堵塞，从而有效地节省能量开销，起到延长网络寿命的作用[5]。

均值估计算法[6]是将网络中多个节点的采样数据进行取均值处理。当采样数据样本足够大时，估计值趋于真值；自适应加权融合算法[7]是基于卡尔曼滤波原理的最小方差意义下递推估计算法，利用总的均方误差最小的条件，自适应地对各个节点权值进行匹配，使得结果达到最优。由于采样真值存在时间上的差异，同时节点间采用的数据值也存在一定的偏差，所以会造成权值估计出现偏差，估计复杂度较高，不适用于传感器节点。基于信任度的估计算法[8]利用了数据之间的偏差程度来估计数据的有效性，最后融合有效数据，得到较为可靠的数据结果，该算法只考虑采样数据的空间相关特性，忽略了节点采样值是一个随机变量和采样方差对数据的影响，得到的结果存在一定的偏差。

文中在现有传感器网络网内融合算法的基础上,根据传感器网络数据间的相关特性，提出了一种基于神经网络的多级融合算法MLFA(Multi-level fusion algorithm based on Neural Network)，利用数据间的时间-空间相关特性对采样数据进行二级融合处理，获得更准确的数据。

1 MLFA算法

1.1 MLFA算法的模型

对采集数据进行相关性的分析，利用传感器网络中终端节点设备采样数据的空间相关性，对同一时间的采样数据进行一致性检验，消除在采样过程中由于设备异常或者损坏导致异常的数据，然后利用神经网络自学习理论对节点方差进行估计，最后匹配权值。算法模型如图2所示。

图2 MLFA算法的原理框图

1.2 基于置信矩阵的初级融合

在传感器网络中，传感器节点容易受到外界环境因素的干扰(包括温度、湿度和天气等因素影响),导致节点采样数据出现不同程度的偏差,甚至出现异常数据，因此,需要对一次采样数据进行初级融合，消除异常数据对融合结果的影响。

假定在监测区域中部署了n个传感器，节点同时采集相同类型的数据。其中状态观测方程如下：

式中：x----一维状态量;

X----n维测量向量，设X=[x1x2…xn-1xn]T；

e----n维测量噪声向量，包含传感器的内部噪声和环境干扰噪声，设e=[e1e2…en-1en]T；

H----已知的n维常向量,设H=[1 1 … 1 1]T。

其中，各传感器的测量值彼此相互独立，且为无偏估计。

式中：xi----传感网络单次采集数据，i=1,2,…,n；

Dij----节点i与节点j采样数据的偏差程度。

Dij越大，表示节点i和j的采样数据值之间偏差越大。由式(2)构建一个偏差矩阵Dn表示一次采样中传感器间的数据偏差程度。

Dij的值越小,表示节点i和j的采样数据越相近，数据间的相关程度越高，故可用1/Dij表征传感器之间的支持程度：

由式(3)可知,vii=0，这里令vii≪vij，由式(4)计算出各个传感器数据间的支持度。由误差矩阵Dn可以得到传感器间的置信矩阵：

由于关系矩阵Rn为非负矩阵，根据Perron-Frobenius定理可知，Rn存在最大的特征值λ>0，且对应正特征向量Z=[z1,z2,…,zn]T，则有RnZ=λmaxZ,由此定义节点i的权值：

由此,单次采样数据的融合结果为：

利用数据间空间相关性并进行数据融合处理，有效消除了异常数据对融合结果的影响。

1.3 基于神经网络的二级数据融合

学习规则[9]：误差修正学习方法是神经网络学习中的一个重要方法，具体描述如下：

式中:λ----学习因子；

dj，yj----第j个神经元的期望与实际输出；

xi(n)----第j个神经元的第i个输入。

由于终端设备都存在采样误差，仅考虑数据空间相关性进行融合时，融合结果的精度依然无法保证，一旦终端节点采样偏差很大，仍然无法得到精确度高的数据。MTFA算法利用神经网络误差修正学习方法[3-8]对节点的方差进行估计，最后匹配权值。

单次采样时，传感器i的方差为：

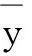
假设终端节点进行m次采样，由于传感器的测量噪声是平稳随机过程，具有各态历经特性，因此，应用神经网络误差修正学习方法对终端节点的方差进行样本训练，更新方差估计值，直到趋于一个稳定值。故传感器i的方差估计值为：

进一步写成递推公式：

其中,学习因子λ=1/m，随着新样本的加入，对传感器方差进行修正，趋于稳定值。然后利用在满足最小均方误差的条件，重新修正终端节点本次采样的权值W。最后由式(11)计算二次融合结果：

1.4 算法的复杂度分析

假设N个传感器节点对同一目标参数进行数据监测，当传感器节点采样一次后进行数据融合时，MTFA算法只需进行N次计算就可以求出传感器方差，计算复杂度为O(N)。与自适应加权融合算法相比显著降低了算法的复杂度。

2 实验仿真与结果分析

文中采用MATLAB进行仿真，仿真数据采用文献[9]的监测参数。文献中的实验参数来自对仓库温度进行监测的实际设备参数指标，具有一定程度的可信度。分别采用均值估计算法、自适应加权融合算法、基于信任度的融合算法和MTFA算法进行数据融合,实验仿真参数见表1。

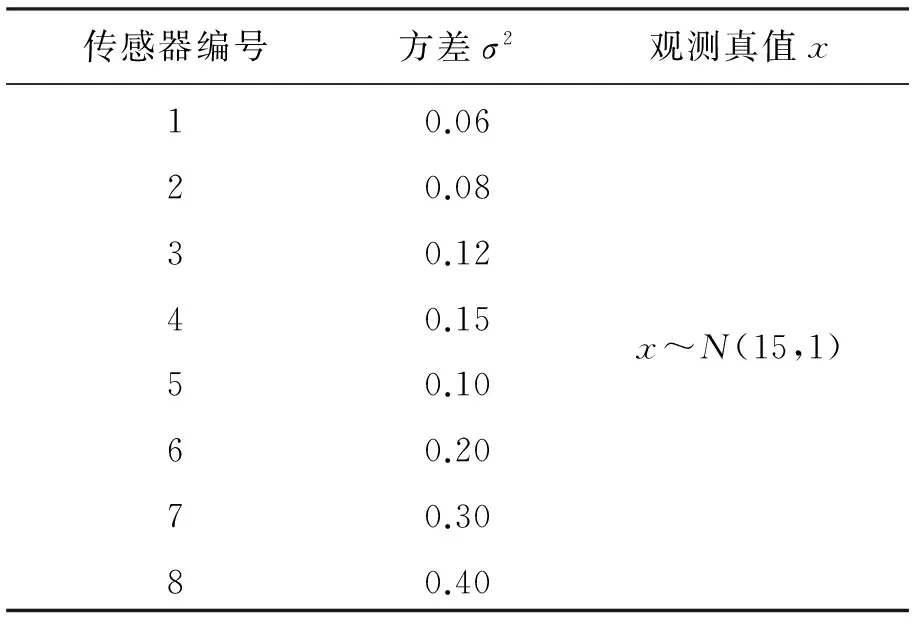
表1 实验仿真参数

2.1 方差估计的有效性

采用MTFA算法时传感器的权重值随采样次数变化的情况如图3所示。

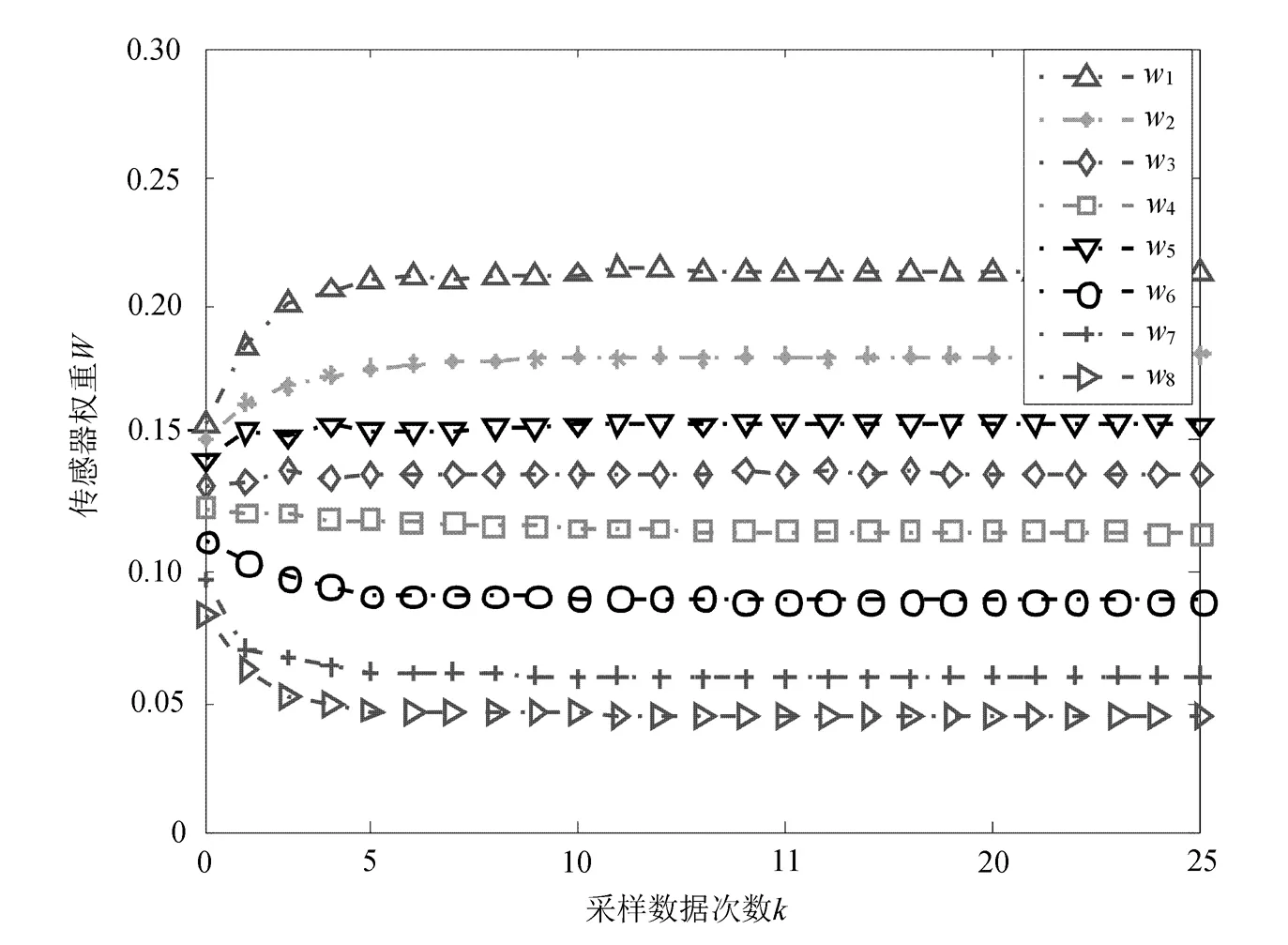
图3 MTFA算法权值随采样次数变化图

由图3可以看出，采样改进的多传感器融合算法随着采样次数的增加，各个传感器的权值趋于稳定值,而且算法的收敛速度快。

LMS算法权值随采样次数变化如图4所示。

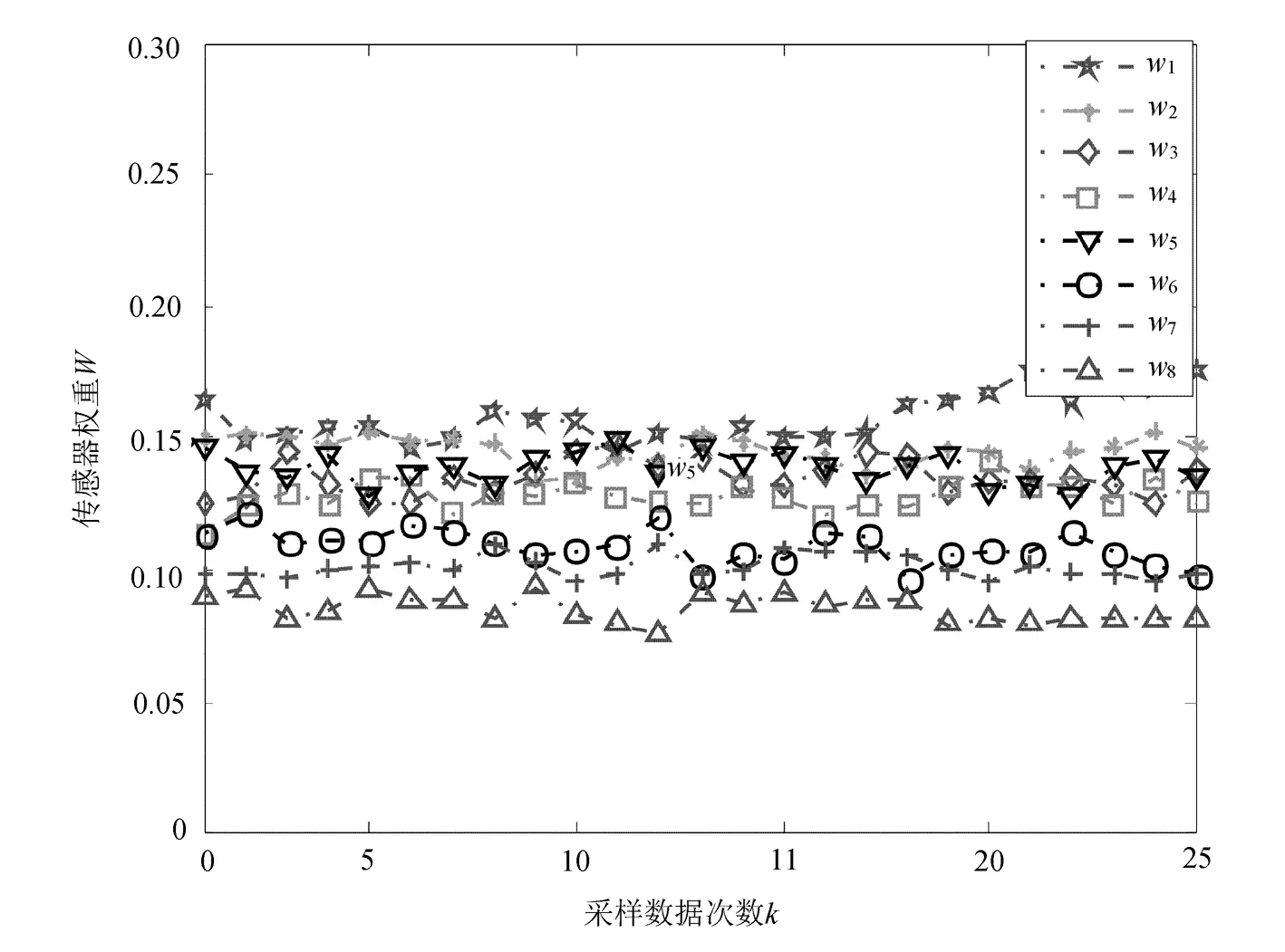
图4 LMS算法权值随采样次数变化图

由图4可知，自适应加权融合算法在目标参数变化的情况下，估计方差值会出现波动现象，方差估计值收敛速度较慢。

仿真结果表明了MTFA算法方差估计的有效性，而且权值收敛比自适应加权融合算法更快，更符合传感器的处理性能。

2.2 融合结果的误差分析

不同算法的融合结果随采样次数的变化情况如图5所示。

图5 不同算法的融合误差比较

由图5可以看出，随着采样次数的增加，均值估计算法、自适应加权融合算法、基于信任度估计算法和MTFA算法的误差值分别为：0.130、0.162、0.165和0.100。

仿真结果表明,当只采用一级融合，即只基于信任度进行估计真值时，融合结果存在较大误差，估计性能甚至比均值估计算法更差，因此有必要进行二级融合。

与均值估计算法、LMS算法和基于信任度融合算法相比，MTFA算法的融合误差最小，融合精度高。因此，MTFA算法在进行融合处理时更具优势，融合结果也更加贴近实际的真实情况，精度更高。特别是在如今的大数据环境中，能够更好地利用数据间的相关性，融合出更准确的结果，有利于作出正确的决策。

2.3 容错性能分析

由于传感器的硬件限制，容易受到人为因素或者自然环境因素的干扰，容易产生异常数据，因此有必要对算法的容错性能进行分析。我们还是用绝对误差作为评价标准。假设第8个传感器的测量方差为5，用来模拟异常数据,实验仿真参数见表2。

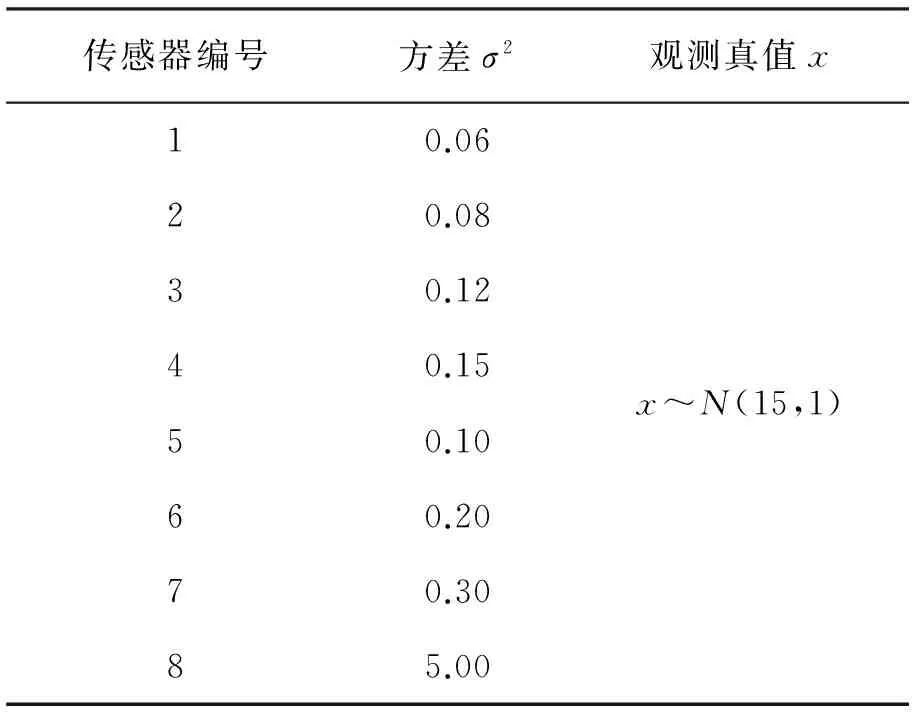
表2 实验仿真参数

异常数据情况下，不同算法的融合结果随采样次数的变化情况如图6所示。

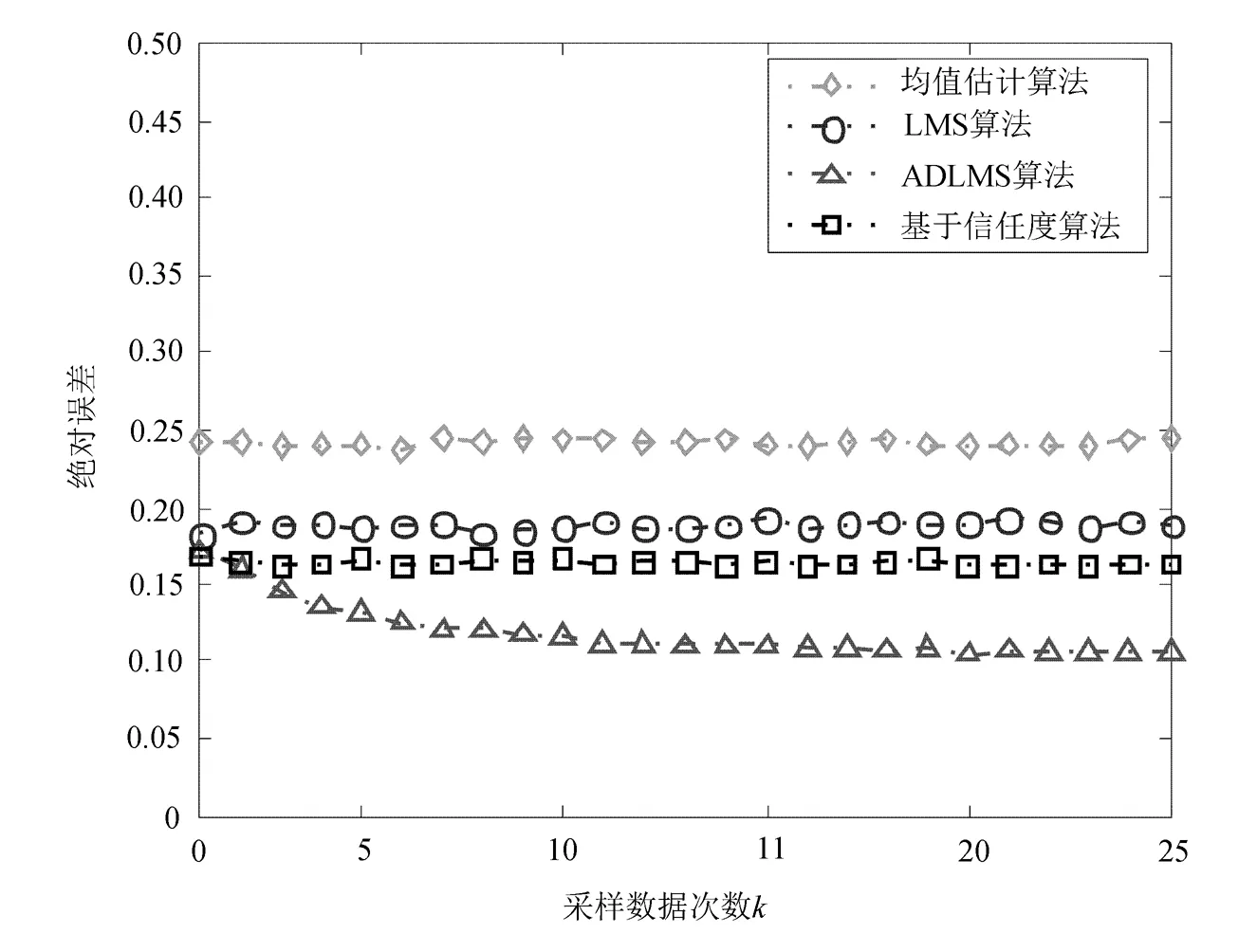
图6 数据异常情况下融合结果的误差曲线

由图6可以看出，当存在异常数据时，采用4种不同的融合算法进行数据融合，融合结果的绝对误差分别为：均值估计算法的误差0.24,LMS算法的误差0.19,基于信任度融合算法的误差0.16,MTFA算法的误差0.10。

仿真结果表明，当存在异常数据时，与其他3种算法相比，MTFA算法的融合误差最小，抗干扰性能最好。因此，MTFA算法具有更好的容错性能。

3 结 语

MTFA算法首先基于置信矩阵利用数据的空间相关性对采样数据进行初级融合，保证数据结果更接近真值，然后利用终端节点的时间相关性，运用神经网络误差修正的方法重新修正权重，算法计算量更小，适合传感器处理。MATLAB仿真实验结果表明，与现有的数据融合算法相比,MTFA算法的融合精度更高，算法的收敛性快，而且在异常数据情况下，文中提出的多传感器融合算法的容错性能更好。在大数据环境下，可以更好地利用数据间的相关性，融合出可靠性高的结果，有利于作出正确的决策。

[1] Yi S, Naldurg P, Kravets R. Security-aware ad hoc routing for wireless networks[C]//Proceedings of the 2nd ACM international symposium on Mobile ad hoc networking & computing. [S.l.]: ACM,2001:299-302.

[2] 高良诚,刘杰,李江华.保证服务质量的无线传感网节能跨层路由算法[J].长春工业大学学报,2016,37(1):63-68.

[3] Singhal D, Garimella R M. Simple Median based information fusion in wireless sensor network[C]//2012 International Conference on.IEEE.[S.l.]: Computer Communication and Informatics (ICCCI),2012:1-7.

[4] 沈丽艳,马春龙.基于数据融合的土壤电导率测量方法[J].长春工业大学学报：自然科学版,2012,33(2):151-154.

[5] Rout R R, Ghosh S K. Enhancement of lifetime using duty cycle and network coding in wireless sensor networks [J]. Wireless Communications, IEEE Transactions on,2013,12(2):656-667.

[6] 曾黎.多传感器数据融合的数学方法研究[J].云南民族大学学报：自然科学版,2010,19(5):321-324.

[7] 张阳,沈明霞,孙玉文,等.基于多传感器自适应加权融合的温室信息系统[J].传感器与微系统,2014,33(6):100-103.

[8] 刘克中,庄洋,周少龙,等.基于节点感知信任度模型的无线传感网络事件检测方法[J].北京邮电大学学报,2015,38(1):61-66.

[9] 陈延伟,施江天,吴艳茹,等.基于神经网络的多传感器信息融合技术在移动机器人中的应用[J].长春工业大学学报：自然科学版,2008,29(5):550-555.

[10] 白玉艳,严伟榆,杨自琼.基于S3C2440和多传感器数据融合的烟叶仓库温湿度监测系统设计[J].安徽农业科学,2012,40(8):5010-5011.

Neural multi-layer data fusion algorithm in wireless sensor network

LEI Yufei

(Quanzhou Institute of Information Engineering, Quanzhou 362000， China)

Based on the corrections among the sensor network data, a multi-layer data fusion algorithm is applied for second-level fusion according to the space-time correction of the data to get more accurate data. Simulation results indicate than the algorithm can meet the needs of data precision under huge data environment.

sensor node; neural network; confidence degree; fault tolerance.

2017-01-25

福建省中青年教师教育科研项目(JAT160613)

雷宇飞(1981-)，男，汉族，福建泉州人，泉州信息工程学院讲师,硕士，主要从事计算机网络、数据库技术方向研究,E-mail:13636926060@163.com.

10.15923/j.cnki.cn22-1382/t.2017.2.10

TP 393

A

1674-1374(2017)02-0155-07