热负荷预测中最有影响力参数测定

张 琦， 谢慕君， 贾其臣， 曹开发

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)



热负荷预测中最有影响力参数测定

张 琦， 谢慕君*， 贾其臣， 曹开发

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

针对集中供热系统，采用自适应模糊神经推理系统分析热负荷的影响因素与系统热负荷之间的相关性和影响程度。分别分析了不同预测时间下的3组输入变量对集中供热系统热负荷预测的影响。仿真结果表明,应用ANFIS选取集中供热系统热负荷预测的输入变量对于简化预测是可行的。

ANFIS； 变量选取； 集中供热系统； 热负荷预测

0 引 言

集中供热系统是一个十分复杂的多变量控制系统，供热面积大，影响因素多，内部关联性强，滞后时间长，非线性严重[1]。集中供热的优点[2]是提高能源利用率，节约能源。集中供热系统一方面为我们提供了热能，但另一方面也对能源造成了极大消耗。在集中供热系统建设中，如果忽视了节能技术的应用，将会导致集中供热系统建设成本的提高，在运行过程中也将耗费更多的能源，这不但影响用户的切身利益，对企业的发展也非常不利。因此，注重节能技术和措施在集中供热系统中的应用是十分必要的[3]。

为了更加有效地使用一次能源，热负荷预测模型必须采用创新、智能的控制策略。热负荷预测模型的建立对集中供热系统的节能优化是非常重要的。如果建立的热负荷模型是可靠的，那么生产的热量将会和用户的真实需求相匹配。这将减少热损失，降低回流温度，并且可能在集中供热系统中连接更多的用户。另外，热负荷预测可以作为集中供热系统模型预测控制的输入，以便更有效地峰调和利用热能存储系统[4]。文献[5]中建立预测模型使用了许多输入变量。热负荷模型的输入变量有室外空气温度、太阳辐射、风向、风速、供水流量、供回水温度、时间和日子类型(周末和工作日)等。输入变量的选择(丢弃冗余和非信息的预测因素)及识别和消除潜在的输入变量之间的多重共线性对于建立预测模型来说是非常重要的。正确的变量选择将会使预测模型更加精准。

文献[6]采用了两种方法选择最佳的变量子集：滤波方法和包装方法。在滤波方法中，模型输入变量的选择是在模型训练和调整之前进行的。包装方法使用一些误差指标评估不同输入变量组合的预测能力，并选择模型产生的最佳结果。包装方法的计算更严苛，特别是针对具有多个调谐超参数的模型，与滤波方法相比，它可以被视为是一个更好的选择。

文中使用包装方法选择出了对集中供热系统热负荷预测模型最有影响力的输入变量，即当前和滞后(最多10步)的热负荷、室外温度和供水流量。应用ANFIS从包装方法中选出的数据集中选择出最主要的模型变量。

1 ANFIS自适应神经模糊推理系统

ANFIS是基于Takagi-Sugeno模型的自适应神经模糊推理系统[9]。该模糊推理系统利用BP方向传播算法和最小二乘算法来完成对输入/输出数据的建模。该系统由模糊规则、数据库和推理机制3部分组成。文中设定的两个ANFIS输入变量是对集中供热系统热负荷影响最大的参数变量。ANFIS结构如图 1 所示。

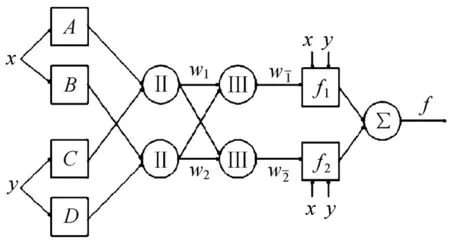
图1 ANFIS结构图

对于一阶的Takagi-Sugeno有两个输入模糊IF-THEN规则[7]：

第1层由输入参数的隶属度函数构成，并且为下层提供了输入值。该层的每个结点都是自适应结点，其节点函数为

式中：uAB(x)，uCD(y)----具有最大值(1.0)和最小值(0.0)的钟型隶属度函数。

例如：

式中：(aibicidi)----参数集合，该层的参数被称为前提参数。

这里x和y是节点的输入，分别代表了两个对集中供热系统的热负荷最有影响力的参数变量。

第2层是隶属度层，它为每一个隶属函数寻找权重。该层接收从上一层传递过来的信号作为该层的隶属函数，然后分别表示每个输入变量的模糊集。第2层的节点是非自适应点，该层作为接收信号的乘法器：

每一个节点的输出表示一个规则的激励强度。

第3层被称为规则层，该层将各条规则的激励强度归一化，该层中的结点也被认为是非自适应的。这里的每一个节点代表一条模糊规则，计算每条规则的适应度，从而使模糊规则的数目等于该层层数。所有规则的激励强度的形式为：

结果被称为归一化的激励强度。

第4层负责提供输出值，作为推理规则的结果,也被称为模糊化层。每个第4层的节点都是自适应节点。在这层中每条规则的输出为

式中：w----从第3 层传来的归一化激励强度；

(pi,q,iri)----节点的参数集，该参数集被指定为结论参数。

第5层称为输出层。这一层的单结点是一个标以∑的固定结点，它计算所有传来信号之和作为总输出。即累加了所有从上一层接收的输入信号。然后，它将模糊分类结果转换成二进制。第5层的单节点被认为是非自适应的。该节点计算出所有接收信号的总输出为：

在ANFIS结构识别变量的过程中应用了混合学习算法。前提参数采用反向传播算法，而对于结论参数则采用线性最小二乘估计算法调整参数。在每一次迭代中，首先输入信号沿着网络正向传递到第4层，此时固定前提参数，采用最小二乘估计算法调节结论参数；然后信号沿着网络正向传递直到输出层。之后将获得的误差信号沿着网络反向传播，并通过梯度递减顺序调节前提参数。进而可以得到结论参数的全局最优点，这样不仅可以降低梯度法中搜索空间的维数，还可以大大提高参数的收敛速度。

模糊神经网络虽然是局部逼近网络，但是它是按照模糊系统模型建立的，网络中的各个节点及所有参数均有明显的物理意义，因此，这些参数的初值可以根据系统的模糊或定性的知识来加以确定，然后利用上述学习算法可以很快收敛到要求的输入/输出关系，这是模糊神经网络与单纯的神经网络相比的优点所在。同时，它具有神经网络的结构，因此参数的学习和调整比较容易，这是它与单纯的模糊逻辑系统相比的优点所在。

2 基于ANFIS的输入变量的选择

2.1 模型输入变量的选择

在实际供热负荷预测时，根据问题需要和数学描述方法来进行恰当的输入变量的类型和数量的选择对达到高品质预测效果至关重要[8]。要建立一个具有最佳特性的预测模型，确定最相关的和有影响力的变量的子集是必要的。这个选择的过程通常被称为变量选择。这个过程的目的是找到初始输入变量集的一个子集，使模型提高预测水平[9]。

由于集中供热系统的动态性，在使用包装方法选出室外温度、热负荷和供水流量这3个输入变量之外，文中引入了潜在的输入变量，即时间滞后值。在初始设置中添加这些变量的滞后值是很重要的。虽然初始设置更多的滞后变量对于系统的预测是有利的，但是考虑到计算机的计算能力和运行时间，因此限制滞后的数量为10。所有潜在的预测因子见表1。

表1 热负荷预测模型的潜在输入变量

2.2 仿真实验

采用长春市某换热站2003年4月1日-2003年4月7日供热数据，测量间隔为1 h。实验数据见表2。

综合分析了热负荷及其他相关参数的影响，对供暖数据进行了处理。本研究创建了3个时间序列：热负荷(MJ/h)、室外温度(℃)、供水流量(t/h)。分别预测了1，3，5，8，12，24 h之后的热负荷。在Matlab环境下完成仿真研究。

文中对热负荷分别进行了单输入和三输入的预测。首先对热负荷进行了单输入的预测，预测结果如图2～图7所示。

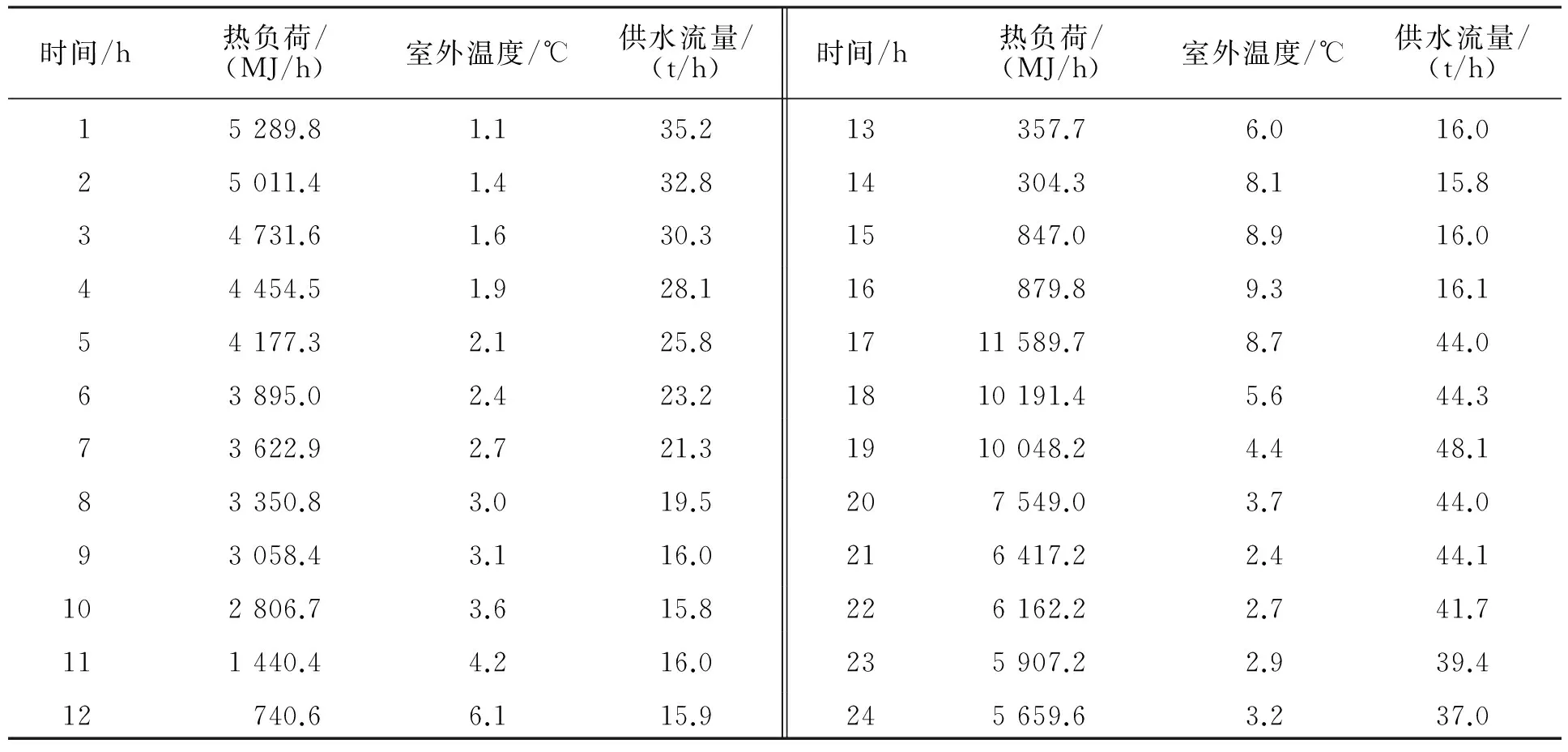
表2 某日24 h样本数据

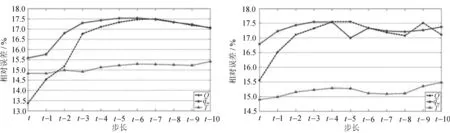
图2 预测1 h后热负荷的ANFIS绝对误差 图3 预测3 h后热负荷的ANFIS绝对误差

图4 预测5 h后热负荷的ANFIS绝对误差 图5 预测8 h后热负荷的ANFIS绝对误差

图6 预测12 h后热负荷的ANFIS绝对误差 图7 预测24 h后热负荷的ANFIS绝对误差

图2～图7显示了所有潜在的输入变量对集中供热系统热负荷预测结果的影响。根据图2和图3显示，对于预测1 h和3 h后的热负荷，影响力最大的参数是没有时间滞后的参数。这意味着目前的热负荷值对于预测来说是足够的。根据图4～图6显示，随着预测时间的变长，影响力最大的参数为时间滞后值。

使用给定的输入变量进行预测，首先，把室外温度和热负荷固定在t时刻，用当前时刻t和滞后时刻的供水流量来建立预测模型，得到所有的预测结果。接下来，固定热负荷在t时刻，使用当前时刻和滞后的供水流量和室外温度建立预测模型。最后，使用所有滞后时间的热负荷交替进行前两步。每个组合都建立了一个ANFIS模型，并且在每一个时间点上分别训练它们。

从表3中能清楚地看出预测结果，进行3组输入变量的负荷预测中，用当前时刻热负荷Q(t)，室外温度T(t)，供水流量qm(t)来预测1 h后热负荷的模型相对误差最小，仅为3.13%。对于预测3，5，8，12 h之后的热负荷模型来说，时间的滞后值成为了最有影响力的参数变量。3组输入变量的ANFIS热负荷预测结果见表3。

表3 3组输入变量的ANFIS热负荷预测结果

3 结 语

如果将一组非相关的或非显著的变量选进输入变量集，会使训练时间加长，导致结果变差，只有找到一组合适的输入变量，才能有效地解释负荷的变化关系，才有可能对各种变化条件下的负荷做出准确预测。针对上述问题提出了以一种ANFIS自适应模糊神经推理系统找出最能影响集中供热系统热负荷预测的参数变量的方法。包装方法是用来从一组可能的输入变量中选择最有影响力的变量的子集。用ANFIS确定在不同预测时间下3组输入变量(滞后10步的热负荷，滞后10步的室外温度，滞后10步的供水流量)对集中供热系统热负荷预测的影响。

结果表明，对于1～3 h的预测来说，当前时间的输入值可以满足预测要求。但是对于预测3 h后的热负荷来说，时间滞后值是热负荷预测中最有影响力的参数。

对ANFIS进行更进一步的细化和改进，可以从加速不同预测模型的训练过程以减少系统运行时间，或者使训练过程包含更多的潜在输入变量和更多的滞后变量这两个方面研究。这些方法都可以提高建立模型的预测能力。还可以着力挖掘热负荷预测中一些新的相关因素。文中提出的分析方法不仅可以进行最相关变量的选取，还适用于超短期负荷预测。

[1] 李天智,孙海波.城市集中供热系统控制策略[J].河北省科学院学报,2000,17(4):205-207.

[2] 赵阁.节能技术和措施在集中供热系统中的应用[J].中国科技纵横,2016(6):200-204.

[3] 冯旭.集中供热与节能[J].资源节约与环保,2007,23(2):54-56.

[4] 李先瑞,李秀.中国城镇集中供热的可持续发展[C]//面向21世纪的热电联产学术交流会.2000.

[5] 高山,单渊达.神经网络短期负荷预测输入变量选择新方法[J].电力系统自动化,2001,25(22):41-44.

[6] Talavera L. Feature selection[C]//Advances in intelligent data analysis VI. Berlin: Springer Berlin Heidelberg,2005:440-451.

[7] 顾秀萍.自适应神经模糊推理系统(ANFIS)及其仿真[J].火力与指挥控制,2010,35(2):48-49.

[8] 孙健,金鑫.探索模糊控制在锅炉热工控制中的应用[J].科技风,2014,19:115-115.

[9] 易继锴，侯媛彬.智能控制技术[J].北京:北京工业大学出版社，2003.

Heat load forecasting input variable selection

ZHANG Qi, XIE Mujun*， JIA Qichen， CAO Kaifa

(School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012， China)

For the central heating system, Adaptive Network-based Fuzzy Inference System (ANFIS) is used to analyze the correlation between the influencing factors of heat load and the heat load of the system. The influence of three sets of input variables on the thermal load forecasting of the central heating system are studied. Simulation results indicate that ANFIS is feasible to be applied to select the input variables of the thermal load forecasting of the central heating system, and simplify the prediction.

ANFIS; variable selection; central heating systems; heat loadforecasting.

2017-02-21

吉林省科技计划重大项目(20126040)

张 琦(1990-)，女，汉族，吉林长春人，长春工业大学硕士研究生，主要从事工业节能控制方向研究,E-mail:619610125@qq.com. *通讯作者：谢慕君(1969-)，女，汉族，吉林长春人，长春工业大学教授，博士，主要从事工业节能控制方向研究,E-mail:1551852633@qq.com.

10.15923/j.cnki.cn22-1382/t.2017.2.09

TU 995

A

1674-1374(2017)02-0150-05