铁路平车装载问题模型及算法

刘宏伟（军事交通学院，天津 300161）

铁路平车装载问题模型及算法

刘宏伟
（军事交通学院，天津 300161）

将平车装载问题抽象为一维装箱问题。针对铁路军事运输中平车装载问题建立了数学模型，并采用Best Fit近似算法、First Fit近似算法和Next Fit近似算法分别求解并比较分析，得出分析结果。

平车装载；算法；优化

1 引言

铁路运输具有运量大、速度快、不易受天候和季节的影响,适合远距离运输等优点,在现代物流中承担着重要的运输任务,同时也是部队兵力机动采用的机动方式之一。研究铁路输送中的列车装载问题模型与算法，并运用于相应的军事辅助决策系统，是适应未来战场、提高指挥效能的客观需要。在铁路运输中经常会遇到轮式（履带式）车辆装备的运输装载问题,为了方便装备的装载及加固,一般选用木质底板的铁路平车进行装运,有些特殊装备对平板车还有专门的要求。在铁路运输中,装载轮式车辆装备可采用顺装、跨装、爬装、横装等方式,大中型车辆装备的装载常采用的是顺装,而其它的装载方式都有严格的限制。目前,对于铁路运输中装载方案的制定,通常由有关人员根据相关规定和经验,采用手工作业方法制定。这种传统的手工作业方法,费时费力,且很难保证所制定的方案为最优方案,有很大的局限性,很难适应现代铁路运输的需要。改革传统的手工作业方式,建立科学合理的模型,并运用于相应的辅助决策系统是一个迫切需求的问题[1]。

2 主要研究方法和技术路线

铁路军事运输平车装载主要考虑两个因素：平车和装备。平车方面主要考虑的有：平车的长度、宽度，平车的载重量。装备方面主要考虑的有：装备的长、宽、高，装备的重量，装备是否超限等。本文在建立模型时，对相关因素进行了简化，只考虑最主要的因素即:平车的长度和装备的长度。综合平车和装备中要考虑的各个因素，联系数学建模理论，建立模型,并对模型进行分析优化，再使用计算机多种近似算法对其进行计算，得出结论，并对结论进行比较分析。

3 铁路平车装载问题模型

平车的装载问题可以描述为有m种装备B1,B2,…,Bm需要装车运输，已知各种装备的数量为V1,V2,…,Vm，在平车上所占的长度分别为l1,l2,…,lm，其重心距装备前端的距离分别为d1,d2,…,dm,重量分别为W1,W2,…,Wm,设有Q种类型平车F1,F2,…,FQ可供使用,各种类型平车的数量分别为N1,N2,…,NQ,长度分别为L1,L2,…,LQ，车辆定距分别为S1,S2,…,SQ,载重量分别为Z1,Z2,…,ZQ,num为所使用平车的数量;xij为在所使用的平车序列中第 j辆平车上装载第i种装备的数量;D为相邻两装备之间所允许的最小间距;aj为第 j辆平车上装备总重心的纵向允许位移量;Yjτ为第 j辆平车上第τ件装备重心到平车前端的距离;Wjτ为第 j辆平车上第τ件装备的重量;ljr为第 j辆平车上第r件装备的重心距其前端的距离;djτ为第 j辆平车上第τ件装备在平车上所占的长度;εj为第 j辆平车上第1件装备的前端距车辆前端的距离[2]。采用顺装方式，可得如下关系：

满足上述要求的可行装载方案有多种,优化的目标就是从所有可行方案中寻求一种使用平车资源最省的方案。由于采用顺装,所以决定在一辆平车上装载装备的多少主要取决于平车和装备的长度。因此,这里可以用平车总长度的利用率作为目标函数,即：

显然，这是一个整数规划问题，而式(1)和式(7)中的求和上标依赖于决策变量num，因此该问题不是一个线性规划问题，也就无法使用传统的分枝定界法来对问题进行求解，必须另外寻找解决问题的办法。该问题可建模为装箱问题,利用BF(Best Fit)算法、FF(First Fit)算法和NF(Next Fit)算法等近似算法对该问题求解。

4 算法分析与设计

铁路平车装载问题实际上可以看作是一个装箱问题，它们在本质上是一致的，就是都是研究装载同样多的货物，怎样装载能使用最少的平车或箱子。

装箱问题是NP完全问题，在多项式时间内不能保证找到最优装箱方案。因此，人们探索求解装箱问题的近似算法，这项工作较早地获得了成功，由于近似算法在解决这类装箱问题中近似度比较小，所以很有实用价值。

大多数装箱问题的近似算法采用贪心策略，即把为了求优化结果进行的总体规划简化为每一步骤的“贪心”处理，即为每次物品装箱规定一种局部选择方法，不同的贪心选择方法产生不同的策略。由于实践中装箱问题的输入长度n较大，近似算法的时间代价与解 的优化程度之间的权衡是很受重视的。下面介绍三种不同的局部优化策略。

4.1 最佳适应（Best Fit，BF）算法

BF策略总是把物品装到能够装下它并且目前是最满的箱子里[3]。

设Si为第i个物品的大小，Bj为第 j个箱子，used(j)为Bj已被占用的部分，则BF策略可描述为：

（1）第一个物品(S1≤1)装到第一个（空）箱子B1中。

（2）下一个物品(Si≤1)装到Bj中，其中Bj满足：

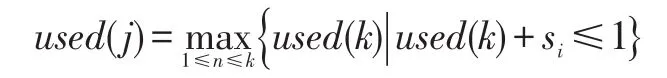
（3）如果i＜n，转到第二步，否则停止。

例如，n=10，S=(0.4，0.2，0.7，0.3，0.5，0.4，0.4，0.3，0.6，0.2)。

采用BF策略设计出的近似算法，其装箱结果如图1所示。

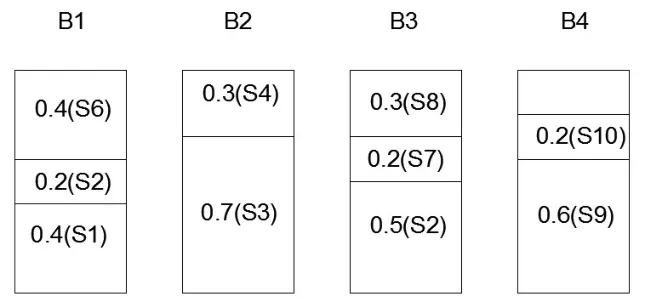
图1 BF算法装箱结果

BF策略的结果较好，但每次要在已装物品的箱子中选取剩余空间最小者，比较麻烦。

Best Fit算法的中心思想是物品装到能够装下它并且目前是最满的箱子里。因此，对于平车装载问题，可以进行如下的设计：

（1）定义变量和数组，准备进行装载；

（2）取出一个装备，准备装载，若无装备了，跳至6；

（3）检查现平车剩余换长是否大于等于装备换长，如果是跳至4，不是跳至6；

（4）把装备装载到现检查平车上，并把原平车剩余换长减去装备换长的值赋于X；

（5）比较X与最小值S，如果X≥S，则跳至6，否则标记当前平车为最合适的平车，然后跳至6；

（6）若现检查平车为最后一辆平车，则将装备装载在现最合适的平车上，现最合适平车的剩余换长等于原剩余换长减去装备换长，然后跳至2；若不是最后一辆平车则，换下一个平车，跳至3；

（7）装载结束。

4.2 首先适应（First Fit，FF）算法

FF策略是把下一个物品放入第一个可以装下它的箱子里，FF策略可以描述为:

（1）第一个物品(S1≤1)放到第一个空箱子B1中(used(1)=0)。

（2）下一个物品，(Si≤1)放到Bj中，其中Bj满足:

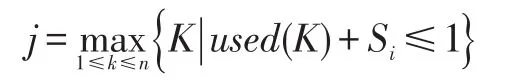
（3）如果i＜n，转到第二步，否则停止。

例如，n=10，S=(0.4，0.2，0.7，0.3，0.5，0.4，0.4，0.3，0.6，0.2)。采用FF策略设计出的近似算法，其装箱结果如图2所示。

由图2可见，FF策略的结果比BF策略多占用一个箱子，但算法执行过程比前者简单。

First Fit算法的中心思想是把物品装入到第一个可以装下的箱子。因此，对于平车装载问题，可以进行如下的设计：

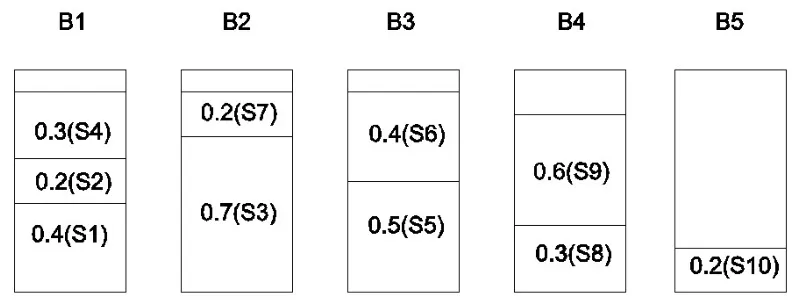
图2 FF算法装箱结果

（1）定义变量和数组，准备进行装载；

（2）取出一个装备，准备装载，若无装备了，跳至6；

（3）检查现平车剩余换长是否大于等于装备换长，如果是跳至4，不是跳至5；

（4）把装备装载到现检查平车上，并把原平车剩余换长减去装备换长的值赋于现平车装备换长，并跳至2；

（5）换下一个平车，跳至3；

（6）装载结束。

4.3 当前适应（Next Fit，NF）算法

在NF策略中，下一个物品的装入只考虑当前的箱子或下一个箱子，这种方法对于所有箱子序列只进行一趟扫描。算法过程描述如下：

（1）i=1,j=1；

（3）如果i＜n，转到第二步，否则停止。

NF算法可能会占用较多箱子，但算法最为简单。例如，n=10，S=(0.4,0.2，0.7,0.3,0.5,0.4,0.4,0.3,0.6,0.2)。采用NF策略设计出的近似算法，其装箱结果如图3所示。

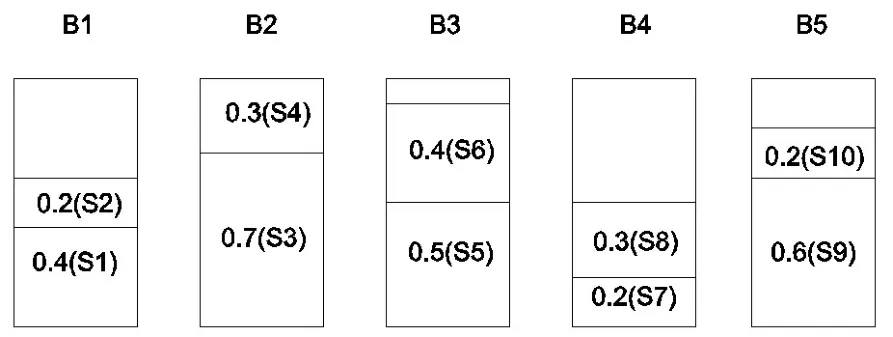
图3 NF算法装箱结果

Next Fit算法的中心思想是物品的装入只考虑当前的箱子或下一个箱子。因此，对于平车装载问题，可以进行如下的设计：

（1）定义变量和数组，准备进行装载；

（2）取出一个装备，准备装载，若无装备了，跳至6；

（3）检查现平车剩余换长是否大于等于装备换长，如果是跳至4，不是跳至5；

（4）把装备装载到现检查平车上，并把原平车剩余换长减去装备换长的值赋于现平车装备换长；

（5）换下一个平车，跳至4；

（6）装载结束。

5 三种算法的综合比较分析

利用平车装载算法演示软件得到的结果见表1。

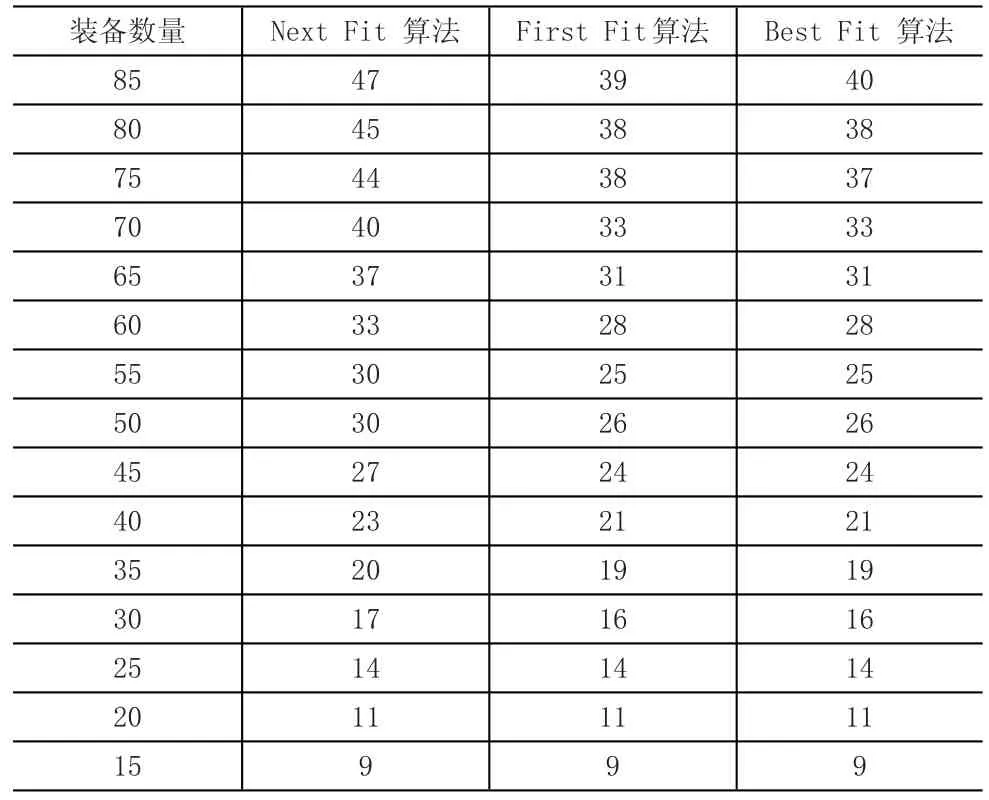
表1 平车装载算法演示软件结果

由图4可以看出，在相同数量和类型的装备的情况下，使用First Fit算法和Best Fit算法所用车数较少。

根据上一部分的数据，可以看出First Fit算法和Best Fit算法的结果都比较优秀。但是根据Best Fit算法的思路，最后得出的结果的平车所有未占用的换长之和是最小的，比较适合铁路平车输送的目标—用最少的平车装载最多的装备。

图4 算法综合比较

6 结论与展望

本文首先根据铁路军事运输的要求，分析了建立铁路平车装载问题模型的必要性和可行性，在此基础上初步建立了铁路平车装载模型，对建模所需的算法进行了设计，并对模型建立时采用的一些算法进行了分析，有以下结论：（1）建立铁路平车装载问题的模型是必要的，也是可行的；（2）在铁路平车装载问题模型的研究过程中，BF算法、FF算法、NF算法可以得到很好的应用；（3）经过初步的研究，BF算法比较适合用来解决平车装载问题。

[1]井祥鹤,周献中,徐延勇,等.铁路输送中平车装载问题的模型与算法[J].计算机工程,2006,(9).

[2]井祥鹤,周献中,徐延勇,多型号平车装载问题的混合遗传算法[J].铁道学报,2006,(12).

[3]刘辉.装箱问题的概率近似算法[J].科学技术与工程,2007, (13).

Model and A lgorithm for Railway Flat Wagon Loading Problem

Liu Hongwei
(Military Transportation Academy,Tianjin 300161,China)

In this paper,in view of the flat wagon loading problem in railway military transportation which we demonstrated could be abstracted into a one-dimension packing problem,we built the corresponding mathematical model,employed respectively the Best Fit approximation algorithm,First Fit approximation algorithm and Next Fit approximation algorithm to solve the model and at the end,analyzed the resultyielded.

flatwagon loading;algorithm;optimization

U294.1;O141.4

A

1005-152X(2017)04-0108-04

2017-03-04

刘宏伟，男，江苏南通人，研究方向：军事交通指挥与工程。

doi∶10.3969/j.issn.1005-152X.2017.04.025