张家港永嘉集装箱码头集装箱吞吐量组合预测

余国刚，冯 琪，徐 粉（武汉理工大学 交通学院，湖北 武汉 430063）

张家港永嘉集装箱码头集装箱吞吐量组合预测

余国刚，冯 琪，徐 粉
（武汉理工大学 交通学院，湖北 武汉 430063）

应用灰色预测模型、二次指数平滑法、BP神经网络预测模型等单项预测方法分别对张家港永嘉集装箱码头集装箱吞吐量进行预测，基于方差倒数法求取每个单一模型的权重，并构建组合预测模型。选择预测误差最小的组合预测模型对集装箱吞吐量进行预测，得出2016年和2017年的集装箱吞吐量预测值。

张家湾永嘉集装箱码头；集装箱吞吐量；灰色预测；二次指数平滑；BP神经网络；组合预测

1 引言

随着世界经济一体化和经济全球化的持续发展，世界各地区港口集装箱运输发展十分迅猛，面对广阔的发展前景和巨大的发展潜力，港口应正确把握集装箱运输发展态势，抓住机遇加快集装箱运输的建设和发展，因此对港口集装箱运输的发展状况进行科学合理的预测，是国家、政府和企业进行集装箱运输建设投资、发展港口集装箱运输的重要决策依据。学者孙永明等[1]建立灰色GM(1，1)模型，对上海港货物吞吐量进行短期预测研究；黄顺泉[2]通过比较分析指数平滑法和回归分析法，对上海港集装箱吞吐量进行预测研究；陈婷婷等[3]建立了三层BP神经网络模型对南京港货物吞吐量进行预测；翟希东[4]在神经系统的相关理论和灰色理论的基础上建立了组合预测模型，得到了较好的预测结果，为集装箱港口的建设与规划提供了合理的决策依据。

张家港永嘉集装箱码头作为张家港港口的一个重要组成部分和上海组合港的重要成员，多年来集装箱吞吐量连续增长，对永嘉集装箱码头集装箱吞吐量进行预测分析，对企业自身而言，有利于公司整合资源，调整集装箱运输发展策略，提高码头竞争力和经济效益；对政府而言，有利于把握港口集装箱发展规模，为制定相关政策提供依据。本文运用多种预测方法，通过比较预测精度，确定出最优组合模型，并对其2016年、2017年集装箱吞吐量进行预测。

2 预测方法选择

在选择集装箱吞吐量预测方法时应考虑以下几点影响因素：

（1）永嘉集装箱码头历年集装箱吞吐量存在着一定的变化规律，且符合时间序列法的特点。

（2）永嘉集装箱码头有限公司成立于1992年，距今仅二十多年，其相关统计数据还不健全。

（3）港口是一个复杂的系统，是一个城市货物集散的物流中心，集装箱吞吐量的发展受多方面因素的影响，包括国家宏观经济水平、地区经济发展水平、外贸进出口总额、其他运输方式运量等。

经分析，本文采用组合预测方法，单项预测模型为灰色预测模型、二次指数平滑法和BP神经网络预测模型，根据单项模型建立组合预测模型，通过分析、比较，确定最优的组合预测模型。

3 集装箱吞吐量预测

张家港永嘉集装箱码头吞吐量增长迅猛，其1998-2015年集装箱吞吐量数据见表1。

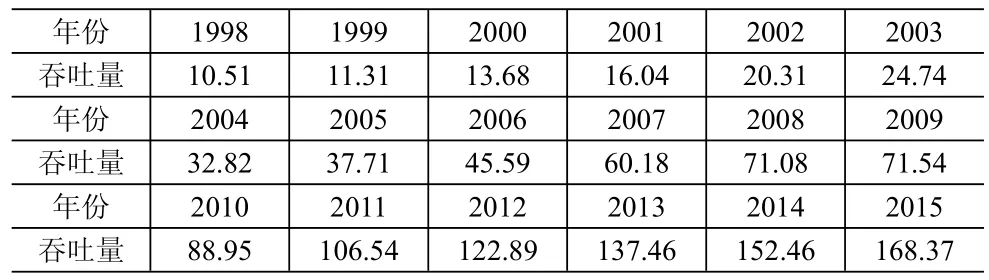
表1 永嘉集装箱码头1998-2015年集装箱吞吐量（单位：万TEU）

3.1 灰色预测模型GM(1,1)

灰色预测模型简称GM预测模型，是通过少量的、不完全的信息，用微分拟合法建立数学模型并做出预测的一种预测方法。灰色预测模型的短期预测结果具有较高的可信度，但是由于其数据量小和信息不完整的缺陷，对于长期预测结果的可信度有所下降。

（1）基本原理

①建模可行性判断。首先判断时间序列是否适合作为GM(1,1)建模序列。对于给定的时间序列X(0)= {x(0)(1),x(0)(2),...,x(0)(n)}，计算级比：

②数据预处理。采用平移处理方法对数据进行处理，处理后数据满足高精度建模序列的要求，即可在原始序列的每一项加一个常数Q，则有：

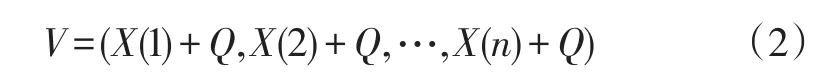
③GM(1，1)模型建立。令X(0)={x(0)(1),x(0)(2),...,x(0)(n)} 为GM(1，1)建模序列，通过累加生成新序列X(1)={x(1)(1), x(1)(2),…,x(1)(n)}，模型相应的微分方程为：

式中，a为发展灰数，μ为内生控制灰数。

④参数估计。设a∧为待估参数向量，α∧=，可利用最小乘法求解，即得：

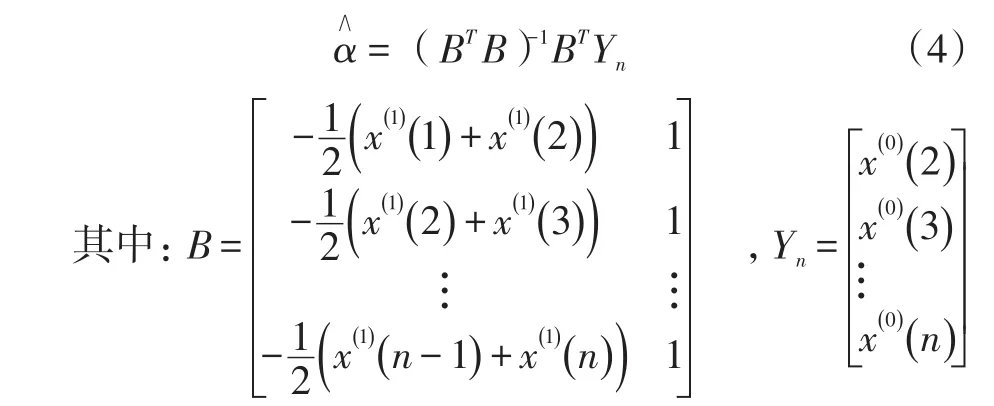
求解微分方程，即可得预测模型：

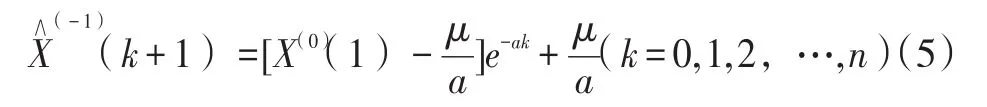
（2）利用灰色模型预测永嘉集装箱码头集装箱吞吐量

选用永嘉集装箱码头2004-2014年数据建立灰色预测模型，经过序列的级比计算发现需要对数据进行预处理，在原始序列的每一项加一个常数Q=100，生成新的数列，新序列的级比已全部落在δ（k）的覆盖范围内，符合灰色预测的要求。

经计算，得到：a=-0.068 4，μ=122.794 2，据此得到GM(1，1)预测模型：

根据式（6）进行计算，计算值进行累减并减去常数Q即为集装箱吞吐量预测值，2011-2015年吞吐量预测数据与实际值的检验分析结果见表2。

3.2 二次指数平滑预测模型

指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测，它对时间序列的随机性和波动性考虑较少。由于永嘉集装箱码头集装箱吞吐量的变化趋向于二次指数平滑变化规律，故本文采用二次指数平滑预测。

表2 灰色预测法预测2011-2015年集装箱吞吐量检验分析

（1）基本原理

①二次指数平滑模型的建立。设时间序列为：x1,x2,x3,...,xn；用S表示指数平滑值，即第t期、第i次指数平滑值记为St(i)，指数平滑值计算公式为（α为平滑系数，且0＜α＜1）：

对预测周期为T年、基年为第t年的指标预测值，其二次指数平滑法的预测模型为：

式中：at，T为预测周期，at、bt为平滑系数。

②平滑初始值的确定。应用二次指数平滑法进行预测时，须首先估算初始值、，根据经验取前3个数据的平均值作为一次指数平滑的初始值，即：

③α值的确定。采用指数平滑法预测，如果数据波动不大，α宜取小值（0.1-0.3），这样可以使各期观察值的权数由近及远缓慢地变小；如果数据波动较大，α宜取大值（0.6-0.8），这样可以加重近期观测值的权数，使各期观察值的权数由近及远较快地变小。但是，在多数情况下α值并不易判断，为准确起见，可分别选用不同的α值试算。

指数平滑法的预测误差可以用均方差法（MSE法）测定，计算公式为：

式中yi为实际值为预测值。对于α值的选定，应以测试数据的预测误差值最小即MSE最小为原则，从中选取较好的α值。

（2）利用二次指数平滑法预测永嘉集装箱码头集装箱吞吐量

选用永嘉集装箱码头2004-2014年数据建立二次指数平滑测模型。经反复检验，最后确定当α=0.8时计算出来的方差最小，最小方差MSE=11.890 0，进而得到预测方程为：

其中（t=1,2,...,n）为预测年份，Y为集装箱吞吐量。

根据式（11）对集装箱吞吐量进行预测，预测数据与实际值的检验分析结果见表3。

表3 二次指数平滑法预测2011-2015年集装箱吞吐量检验分析

3.3 BP神经网络预测模型

人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型，是用大量简单的单元构成的非线性系统，模仿人脑神经网络的结构与功能特征的一种技术系统，是大规模并行的非线性动态系统，具有学习、记忆、计算及智能处理的功能。与指数平滑法、曲线拟合法等方法相比，人工神经网络本身具有一些特性，使其较好的实现了对非线性复杂系统的预测。

GDP、对外贸易额、第一产业产值、第二产业产值、第三产业产值、货运量、水路货运量对于张家港永嘉集装箱码头集装箱吞吐量有极其重要的作用，本文选取1992年-2015年的影响因素统计资料，把它们作为BP神经网络的输入值，2011年-2015年的货物吞吐量作为输出值。1992年-2015年的影响因素统计资料见表4、表5。

BP神经网络预测具体步骤如下：

（1）数据预处理。将各影响因素统计值与吞吐量统计值进行归一化处理，使其数值在0-1之间。

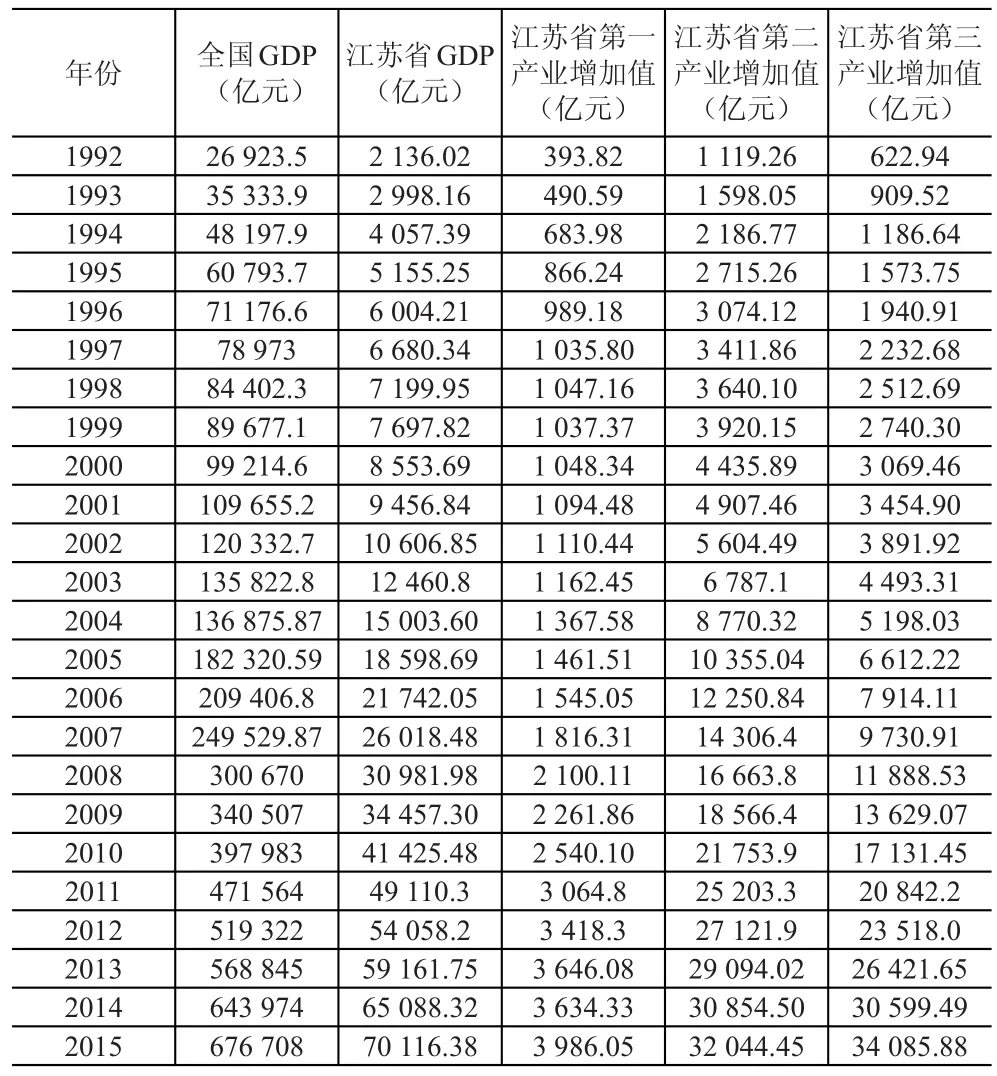
表4 集装箱吞吐量影响因素统计表（1）

表5 集装箱吞吐量影响因素统计表（2）

其中，Xi为原始数据，Yi为预处理后的数据，是根据实际情况取得的小于数据中最大值的数值。

（2）样本的选取。本文用前十年的影响因素作为网络的输入值，第十一年集装箱吞吐量作为输出值。首先将1991年-2000年的影响因素作为训练样本的第一次输入，将2001年的集装箱吞吐量作为第一次输出，依此类推，得到14个样本，选取前10个样本为训练样本，后4个作为测试样本。

（3）网络参数设置。设定最大训练次数为10 000、训练精度为0.000 000 1。对于隐含层神经元个数的确定，本文采用的是试探法。首先用经验公式来确定大致范围，然后从隐含层神经元个数少的网络开始训练，逐渐增加节点数目，并且分析每次结果的误差，如果误差没有因节点的增多而增大，此时的神经元个数可以认为是理想的。

其中，输入层节点数m=50，输出层节点数n=1，C为1-10的节点数。

经过计算与训练，确定隐含层神经元个数为16时，训练次达到7 365次时达到设定的目标误差，训练结果如图1所示。

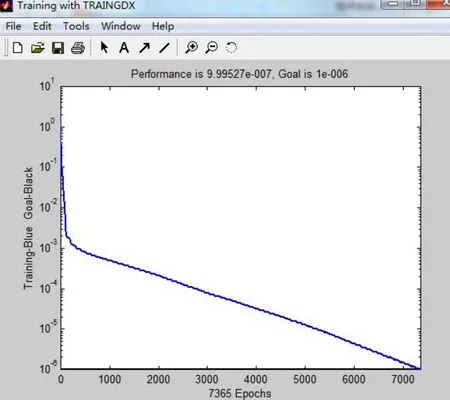
图1 神经网络训练结果图

（4）选择后四个样本作为检验样本，要求输出值与实际值误差在1.5%以内。分别将影响因素数据作为输入，输出2011年-2015年集装箱吞吐量，并检验精度是否达到要求。

经过计算与调试，达到预测精度要求时，用2011 年-2015年数据进行检验，检验结果见表6所示。

3.4 组合预测模型

组合预测是通过对单项预测模型进行组合来尽可能地提高预测精度的预测方法，研究表明，在诸多单项预测模型各异且数据来源不同的情况下，组合模型的预测结果比任何一个单一模型的预测精度都高，组合预测模型具有减少预测系统误差，显著改善预测效果的作用。

表6 预测2011-2015年集装箱吞吐量检验分析

为了能充分利用以上三种模型的优点，有必要将它们进行组合。组合预测的关键是确定加权系数，可以根据不同的理论确定不同的计算方法，本文采用方差倒数法即预测误差平方和来确定加权系数。预测误差平方和是反映预测精度的一个指标，预测误差平方和越大，表明该预测模型的精度越低，从而它在组合预测中的重要性就越低，重要性的降低表现为它在组合预测模型的组合预测中应赋予较小的加权系数。

（1）基本原理。设Y为预测对象的各种预测方法，则最优综合模型为：

其中Qi=，式中Qi分别为预测方法在综合模型中的权重，Di为每种预测方法的误差平方和。

（2）组合模型的建立。基于以上所建立的三个单一模型，可以建立四种不同的组合模型，分别为灰色预测法与二次指数平滑法所建立的组合模型一；灰色预测法与BP神经网络预测模型所建立的组合模型二；二次指数平滑法与BP神经网络预测模型所建立的组合模型三；灰色预测法、二次指数平滑法与BP神经网络预测模型所建立的组合模型四，见表7。

3.5 基于最优组合模型的集装箱吞吐量预测

由表7可知，三个单项模型中灰色模型和BP神经网络模型的预测精度较高，而指数平滑模型预测结果相对较差。通过比较单项模型和组合模型的预测结果可以看到，组合模型明显提高了预测精度。而各种组合之间的比较表明，组合模型四预测误差最小，最小误差为0.733 2%，因此选择综合模型四作为永嘉集装箱码头集装箱吞吐量的预测模型。

表7 三个单一模型和四个组合模型

根据已建立的单一模型和组合模型四，对永嘉集装箱码头2016年和2017年吞吐量预测，预测结果见表8。

表8 永嘉集装箱码头2016年-2017年集装箱吞吐量预测（单位：万TEU）

由表8可知，2016年永嘉集装箱码头集装箱吞吐量为188.48万TEU，2017永嘉集装箱码头集装箱吞吐量为207.53万TEU。

[1]孙永明,郑光平.基于灰色理论的港口吞吐量预测研究[J].中国水运,2007,5(4):160-162.

[2]黄顺泉.关于港口吞吐量预测方法选择的探讨[J].集装箱化, 2003,(7):17-18,28

[3]陈婷婷,陈漪翊.基于BP神经网络的港口货物吞吐量预测[J].计算机与现代化,2009,(10):4-5,9.

[4]翟希东.港口集装箱吞吐量预测模型研究[D].大连:大连理工大学,2006.

Combination Forecasting of Container Throughput of Zhang jiagang Yongjia Container Port

Yu Guogang,FengQi,Xu Fen
(SchoolofCommunication,Wuhan University of Technology,Wuhan 430063,China)

In this paper,we used the grey forecasting model,second exponential smooth method,BP neural network forecasting model, etc.,to forecast the container throughput of the ZhangjiagangYongjia container port respectively,then based on the inverse variance method, obtained the weight of each model to build the combination forecasting model,and at the end,after identifying and using the combination forecasting model with the least forecasting error to forecast the container throughput of the port,arrived at the forecast container throughput of theportfor 2016 and 2017.

Zhang jiagang Yongjia container port;container throughput;grey forecasting;second exponential smooth;BP neural network;combination forecasting

U169.6;F224.0

A

1005-152X(2017)04-0103-05

2017-02-16

余国刚，男，武汉理工大学学术型硕士，研究方向：交通运输规划与管理。

doi∶10.3969/j.issn.1005-152X.2017.04.024