一种自适应的机器人曲面切削力控制算法*

陈首彦 张铁

(华南理工大学 机械与汽车工程学院， 广东 广州510640)

一种自适应的机器人曲面切削力控制算法*

陈首彦 张铁†

(华南理工大学 机械与汽车工程学院， 广东 广州510640)

为提高机器人复杂曲面的切削加工质量，对机器人切削状态进行分析，提出了一种自适应的曲面切削力控制方法.首先探讨了机器人刚度和进给速度对切削质量的影响，建立了冲击和稳态切削状态的动力学模型；然后根据切削形变与进给速度的关系，建立了基于模糊PID的力控制模型；最后通过传感器的力反馈计算出切削形变，实时调整进给速度实现切削质量控制.将文中方法与曲面切削开环控制和PID控制方法进行对比，结果显示，与开环控制和PID控制对比，基于模糊PID的曲面切削力控制方法能有效减小切削过程中刚冲击力幅度和稳定切削的力波动，实现有效的曲面切削力控制.

曲面切削；切削质量；进给速度；机器人形变；模糊PID力控制模型

工业机器人在打磨、抛光、搬运等接触性加工场合得到了广泛的应用，如何在机器人末端与环境保持接触的前提下，实现机器人末端位置和接触力的控制，使机器人具有柔顺控制能力，成了机器人切削应用的关键[1].国内外许多学者已对机器人末端接触力的控制问题进行了相关研究，Domroes等[2]分析了机器人切削位置控制和力控制的区别，探讨了切削力与材料去除速率的关系；Jung[3]提出了一种基于位置反馈的内外环阻抗控制模型，提高了机器人系统的鲁棒性.然而工件形状的多变容易引起切削形变及振动，传统力控制策略无法驱使机器人快速进入稳定切削状态；针对此问题，Karayiannidis等[4]提出一种自适应力控制策略，通过力反馈、位置速度信息对工件表面参数进行学习，从而减少振动周期实现切削力的快速收敛；Kiguchi等[5]则在模糊神经网络智能算法的基础上提出了一种力位混合控制策略，利用神经网络和模糊规则对加工环境进行学习，实现机器人未知环境的抛光加工应用；李二超等[6]则提出了一种力/位混合控制策略，通过力反馈信息判断机器人末端位置，并通过模糊推理确认控制因子以实现机器人的柔顺控制.

然而，上述相关研究并未提到机器人弱刚性对切削精度的影响.实际上，Liu等[7]在早期的研究中就指出，机器人弱刚性容易在接触性加工过程中引起形变波动，导致其无法按照规划轨迹进行高精度的切削加工，特别是工件形状不确定或刀具不平整的情况；为此，Rafieian等[8]研究了刚性平面切削过程中，切削力的波动情况，通过分析砂轮转速、砂轮平整度和振动力波动频率关系，建立了机器人磨削系统非线性刚度模型，并探讨了机器人磨削振动对加工精度的影响；Bigras等[9]对机器人作业环境进行辨识，推导出机器人刚度模型，并利用双重迭代矩阵对力控制进行了优化；Pliego等[10]分析了力位控制策略在未知环境中的位置和力偏差情况，提出了机器人与刚性表面接触时的自适应方法，该方法通过力实时信息判断机器人和约束表面的位置关系；李正义等[11]则针对环境阻尼和刚度变化问题，提出了一种基于递归最小二乘法的自适应阻抗控制方法，实现对环境变化的自适应.

机器人弱刚度对切削精度的影响较大，而关于此方面的力控制方法研究仍然较少.因此本研究将首先对机器人切削动态进行分析，探讨机器人进给速度和刚度对切削形变的影响.文中将机器人切削分为刚性碰撞状态和稳定切削状态，在整个切削过程中存在切削形变的形成和释放，而进给速度的变化将改变形变释放的程度并最终影响加工质量；基于此结论对切削状态进行了分类和模糊化，建立了模糊PID(Proportion-Integral-Derivative)力控制模型，将切削力作为控制输入，根据机器人刚度矩阵计算切削形变引起的加工误差，实时调整进给速度，从而实现切削质量控制；为了确认模糊PID力控制的有效性，进行了开环控制的曲面切削实验以及基于PID控制的切削实验，并将其实验结果与模糊PID力控制效果进行对比.

1 切削状态分析

1.1 机器人切削形变

如图1所示，机器人以进给速度Vw切入工件，刀具挤压工件并进行切削加工，此时，由于刚性较差，机器人受到工件的反作用力.产生挠度β(mm).未能到达规划深度ap(mm)；该过程的切削力波动情况如图2所示.其中F为切削力，t为时间.

由图2可见，切削力首先迅速提升，在编码器读数显示机器人到达规划深度ap时，切削力达到最大值10 N；随后切削力回落进入阶段1的振动状态，经过一定时间后，开始稳定切削(阶段2).根据切削力变化情况可推测出，虽然编码器显示机器人已到达目标规划位置，但切削加工仍在进行，且持续了一段较长的时间.这是由于切削力引起的机器人形变存在释放的过程，该形变的释放速度与材料去除速度有关.

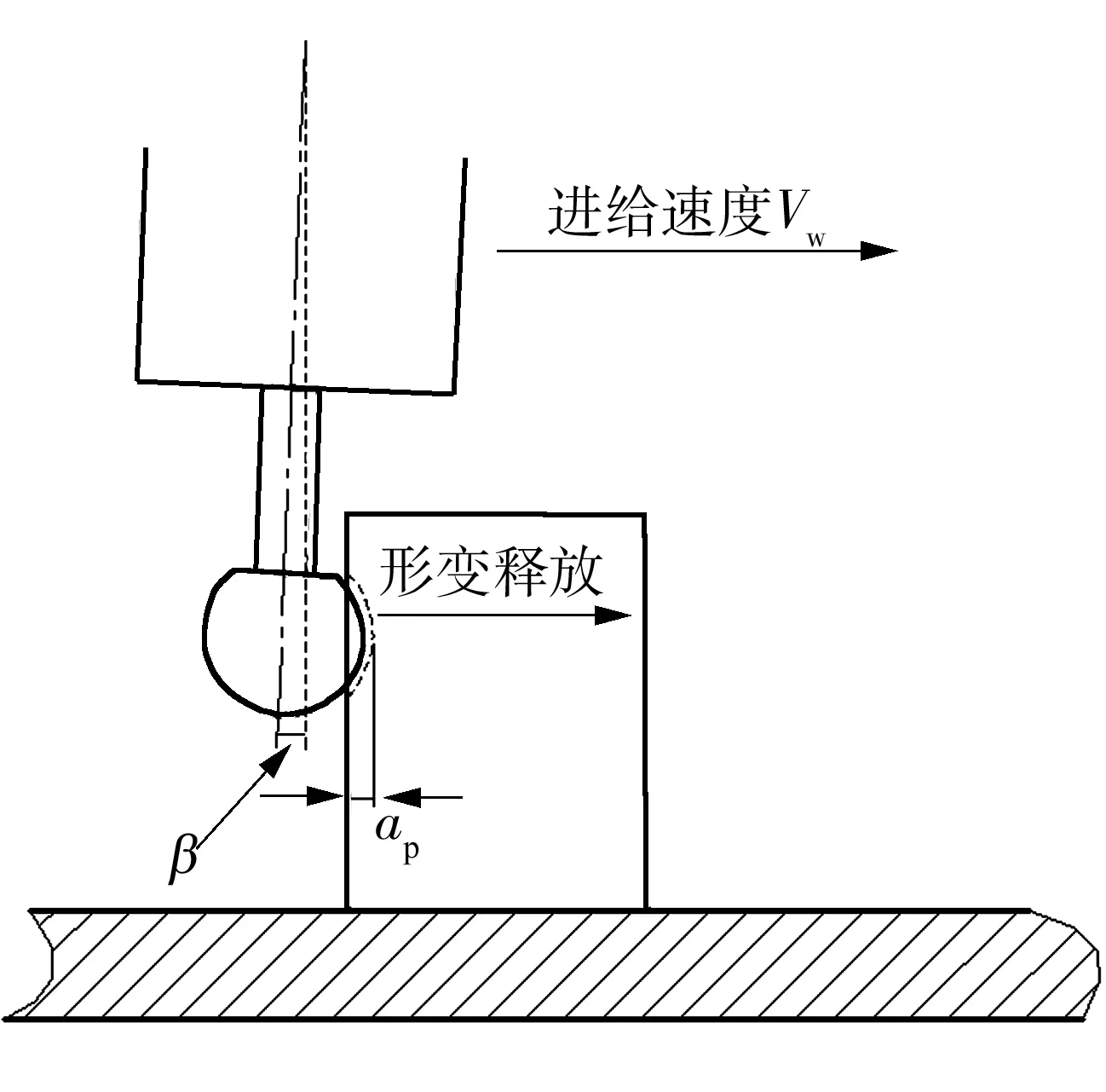
图1 切削形变示意图

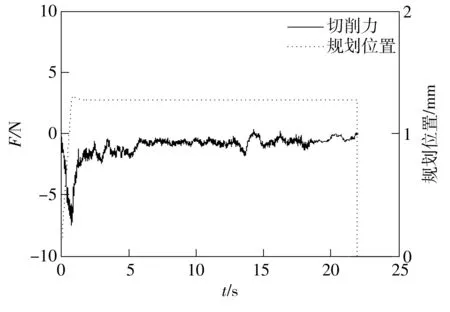
图2 机器人切削规划深度及受力图

设工件对机器人产生反作用力Fp(N)，机器人切削系统受力产生挠度β(mm)，并导致工件部分区域σt(mm)未能完成切削加工，材料去除速度Ve(mm/s)，则t时刻由于机器人形变引起的σt可表达为

Fp=Kσt=K∫(Vw(t)-Ve(t))dt

(1)

式中,K为机器人刚度(N/mm).假设进给速度Vw，则可推导出t时刻的切削力Fp(t)、机器人刚度K、材料去除速度Ve(t)以及形变σt(t)之间的关系为

(2)

在曲面切削过程中，弹性形变将导致实际轨迹与规划轨迹存在偏移，在曲线轨迹插补过程中会产生如图3所示的情况.通过上文分析可知，机器人切削包括稳定切削状态以及冲击振动状态，且由式(1)、(2)可知切削力大小、形变幅度与机器人刚度有关，因此需要对两种状态进行分析，并建立机器人刚度矩阵.

1.2 稳定切削状态

图3 机器人形变对加工轨迹的影响

切削力主要受切削深度ap、进给速度Vw、刀具旋转速度Vs的影响，目前较为广泛的切削力公式为[12]

(3)

其中：μ为材料切削系数；α、φ、γ为经验参数.

然而，由于机器人系统刚度较差，在切削过程中存在弹性形变释放过程，实际切削深度asp可表示为

asp=ap-∫(Vw(t)-Ve(t))dt

(4)

因此式(3)可表示为

(5)

切削过程的动力学模型可表示为

(6)

其中,m为系统质量，C为阻尼系数，Kc为切削系统等效刚度.由式(4)、(5)，当切削深度ap、刀具转速Vs恒定时，切削形变产生的加工误差e=σt(t)受到进给速度Vw的影响.因此可以根据机器人末端刀具受力实时计算出形变状态，通过调整Vw实现加工形变误差控制.基于上述结论，实验采取的切削加工方式如图4所示，刀具最大线速度方向与工件表面切向角度不变，以Vw、Vs、ap对工件进行切削加工，其中Vs、ap为常量.

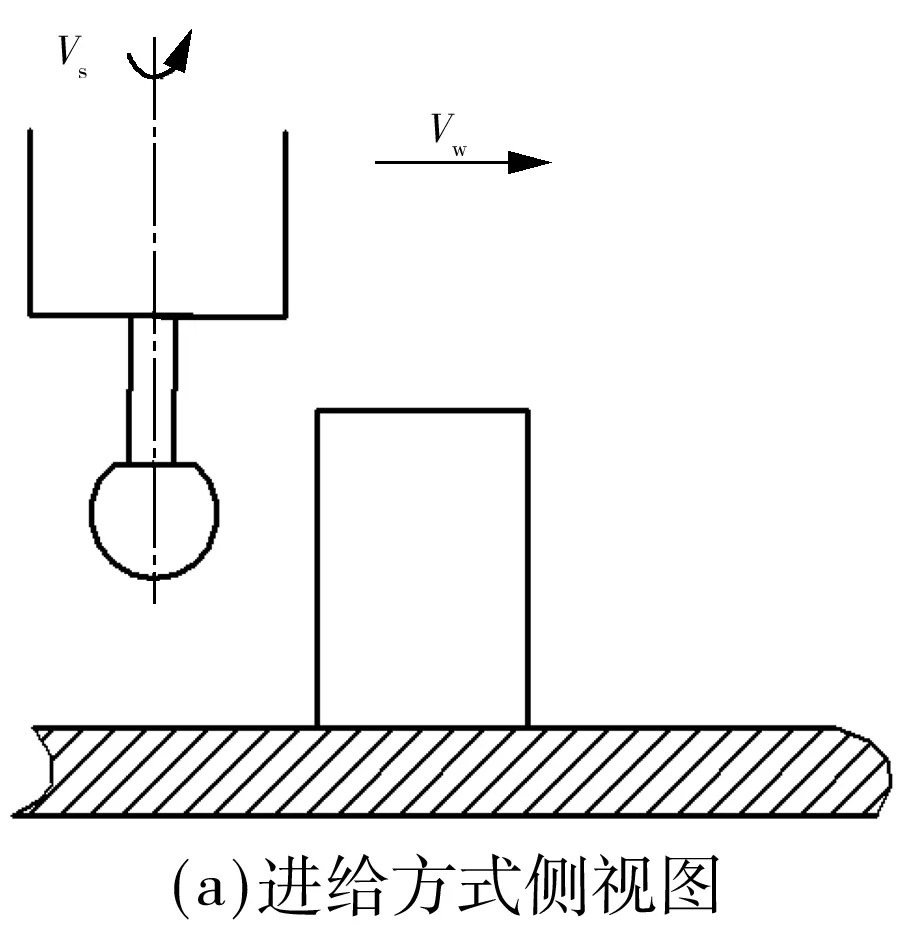
1.3 刚性碰撞状态

由于机器人系统为开环结构，刚度较差，在刀具与工件接触挤压的过程中，旋转中的刀具对其造成冲击，此时，机器人受到工件的反作用力后容易产生瞬时形变，其振幅可以表达为

A=Ac+Az

(7)

其中：Ac为进给速度引起的冲击振幅；Az为离心力引起的振幅.由于Vs恒定，Az可看作是常量.根据动力学原理[13]可知Vw引起的冲击振幅为

(8)

其中：Xc为工件受冲击部位的初始位移；ωd为系统固有频率.

设初始位移Xc为0，因此式(8)可改写为

(9)

由于固有频率ωd及离心振幅Az恒定，因此冲击振幅的控制系数受到进给速度的影响.其动力学模型可表示为

(10)

其中,Kc为切削系统等效刚度.

由式(6)、(10)可知，刚度是影响机器人切削振动的主要因素之一，因此有必要对机器人结构进行分析，并建立机器人刚度矩阵.

1.4 机器人刚度矩阵

由前文可知，机器人切削力大小、实际切削深度与机器人系统刚度存在耦合关系，要对切削深度进行有效控制，首先需要建立机器人刚度矩阵K.如图5所示，实验使用的机器人是在XYZ三平移轴的基础上增加了A、B两轴旋转平台拓展而成，机器人Z轴末端装有三维力传感器和电动切削工具，其中力传感器轴向与切削工具轴向重合，而曲面工件安装在转动平台上.机器人系统刚度主要受到连杆刚度、传动系统刚度及切削工具刚度的影响.在机器人工作范围内，连杆刚度和轴承刚度可近似地认为足够大，因此机器人刚度主要由滚珠丝杠等效刚度Kg、切削工具等效刚度Kj；传感器刚度Kc串联而成：

(11)

图5 机器人切削系统结构

1.4.1 滚珠丝杠刚度

滚珠丝杠刚度由丝杠扭转刚度、轴向刚度以及径向刚度组成.设滚珠丝杠扭转刚度为Kn、轴向刚度为Kt，其中[14]

Kn=Gg

(12)

Kt=Eg

(13)

式中：Gg为剪切弹性模量；dg为丝杠的等效直径；Lg为丝杠长度；Eg为弹性模量；L1为载荷作用点至止推支承的距离.因此直角坐标机器人滚珠丝杠等效刚度为

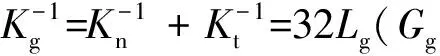
(14)

1.4.2 切削工具刚度

切削工具结构如图5所示，在切削过程中，其主要受到X及Y方向的切削力，因此其切削形变主要来自其扭转刚度，可看作是不同直径圆柱弯曲刚度的串联叠加，其中单个圆柱弯曲刚度为

(15)

式中：Eq为各圆柱部分弹性模量；Iq为切削工具上各个不同直径圆柱体的极惯性矩;Lq为相对应的有效长度.将切削工具等效刚度看作是多个圆柱弯曲刚度之和:

(16)

其中:q=1,2,…,n,n为圆柱体数量.将式(14)及(16)代入式(11)得机械切削系统等效刚度：

(17)

2 自适应模糊PID切削力控制

(18)

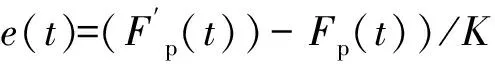
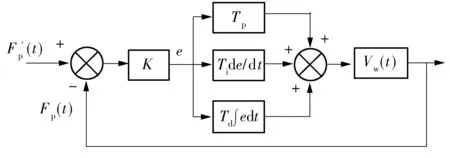
图6 PID控制模型

然而，切削是一个复杂的动态过程，其精确数学模型难以确定，传统的PID控制模型中Tp、Ti、Td无法实时调整，难以快速适应曲率变化，造成切削力的非周期性波动，最终影响加工质量.因此，采用了模糊PID控制策略对曲面进行切削，其实质是根据传感器的力反馈，通过模糊判断规则对切削状态进行判断分类，实时调整PID控制系数Tp、Ti、Td，实现加工误差的模糊控制.其控制模型如图7所示.

图7 模糊PID控制模型

IF A1 and B1 Then C1

IF A1 and B2 Then C2

而对于控制量Ti1、Td1则采用单前提单规则，即

IF A1 Then C1

IF A2 Then C2

为保证切削力的平滑控制，模糊隶属函数采用高斯函数，计算出隶属度后，采用最大隶属度进行解模糊.同时，机器人切削实际上是由刚体冲击碰撞以及稳定切削状态组成，因此为了驱使切削力波动快速收敛，需要为两种状态分别设置控制参数.其中，Tp1、Ti1、Td1为冲击状态下的控制参数，用于减小刀具冲击振动周期，驱使机器人快速挤压工件进行切削；Tp2、Ti2、Td2为稳定切削状态下的控制参数，其用于对稳定切削过程中的力控制.控制过程如图8所示，首先通过力传感器收集机器人末端受理情况，根据机器人刚度矩阵计算出切削形变，判断切削状态.随后根据初步实验得到的模糊规则确定PID控制参数，实现PID控制器的自适应调整，改变切削进给速度，实现机器人切削的自适应控制.

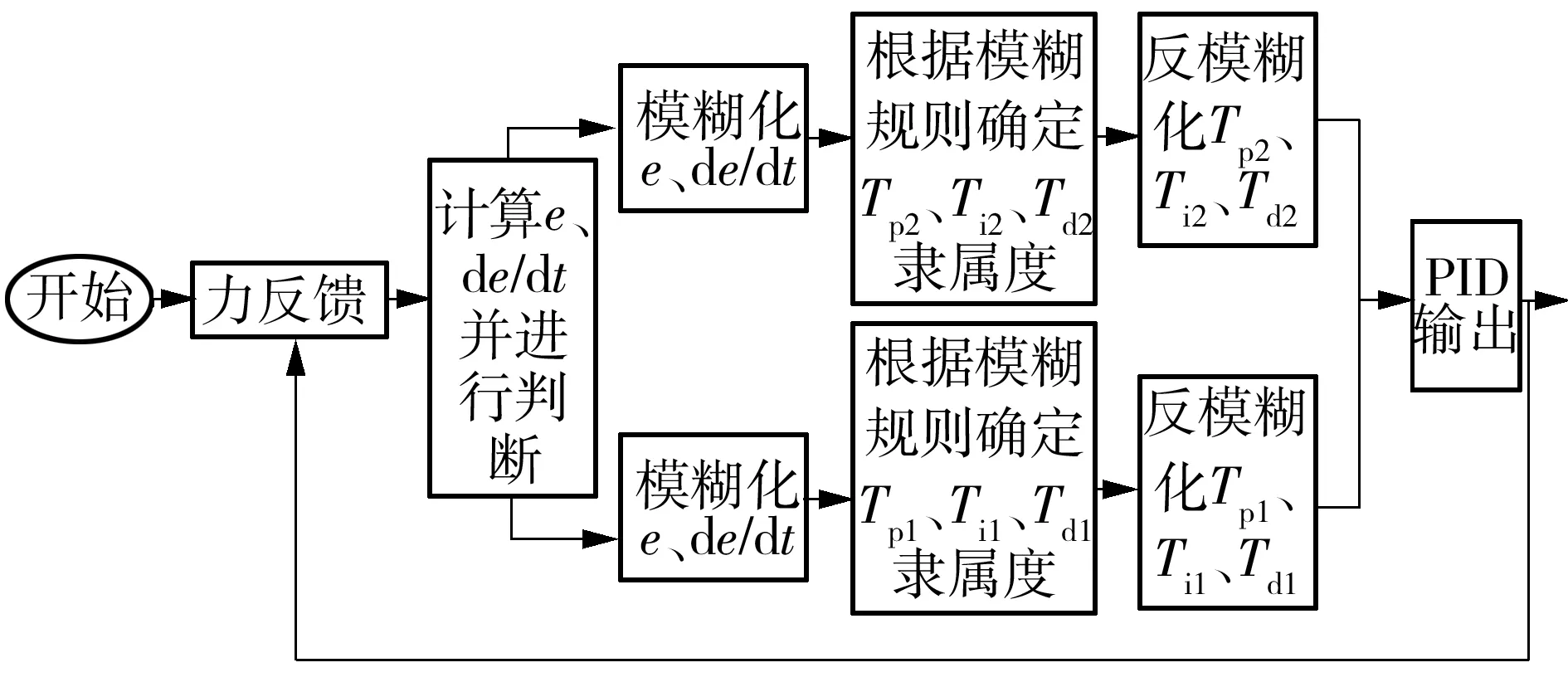
图8 模糊PID控制流程图

3 机器人曲面切削实验

3.1 机器人切削系统

实验用机器人切削系统主要包括直角坐标机器人及其扩展旋转系统、力传感器、切削工具、曲面工件.轴A、B与常用的工业机器人一样，为刚度较弱的开环结构，当受到环境作用力时，容易产生形变，能较好地反应出机器人受力变形过程对切削加工精度造成的影响.以XYZ正极限位置为原点O，以加工平台垂直方向为Z轴，建立世界坐标系OXYZ，如图5所示.相关设备尺寸：X/Y轴滚珠丝杆长980 mm，外径20 mm，导程20 mm；Z轴滚珠丝杆长340 mm，外径15 mm，导程10 mm；六轴力传感器为德国ME-FK6D40，XY方向量程为500 N，Z轴方向为200 N.电动刀具可看作4个圆柱的组合体，直径和长度分别为65和115 mm、52和33 mm、16和39 mm、6和21 mm.曲面切削实验的切削参数为刀具旋转速度4 000 r/min，切削深度0.4 mm，规划进给速度为2 mm/s.

3.2 机器人切削实验

为了验证模糊PID策略的有效性，文中实验切削对象为铝合金样条曲面工件，其曲率的非线性变化，有助于观察力控制策略的实际效果，工件形状如图9所示，利用软件SolidWorks绘制而成.

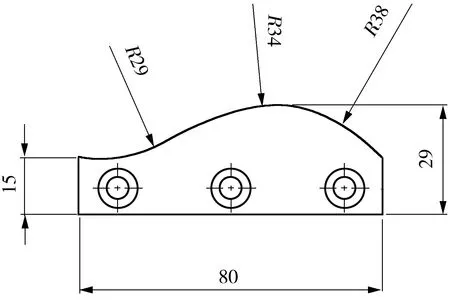
图9 曲面工件(单位：mm)

首先进行了开环控制的曲面切削实验以及PID力控制切削实验作为模糊PID力控制的效果对比.开环控制实验结果如图10所示.

图10 开环控制的曲面切削实验结果

由图10可见，切削力变化的整体规律符合前文对机器人切削的动态分析，存在刚性碰撞阶段和稳定切削阶段.当刀具接触工件时，刀具切削力及进给速度对工件造成冲击，进入刚性碰撞状态，碰撞状态下的切削力峰值达到13 N；随后进入振动切削阶段，力波动大概为6 N，平均切削力约为3.5 N；随着切削的进行，振荡逐渐减小，并进入稳定切削状态，力波动幅度减小至3 N，而平均切削力存在波动，波动范围大概为2.0～3.5 N.

随后进行PID控制切削实验，实验结果如图11所示.由图11可见，碰撞状态下的切削力峰值最大达到8 N，较开环控制的冲击力减小5 N，而力波动最大幅值达到5 N，减小了1 N.在随后的切削过程中，力波动逐渐减小至3 N左右，而平均切削力则在2.5～3.5 N范围内变化.从切削力反馈信息可以看出,PID控制能一定程度上减小冲击振动，并稳定切削状态，但冲击振动周期仍然较长，固定的PID参数难以驱使切削力快速收敛，造成切削力的持续波动.

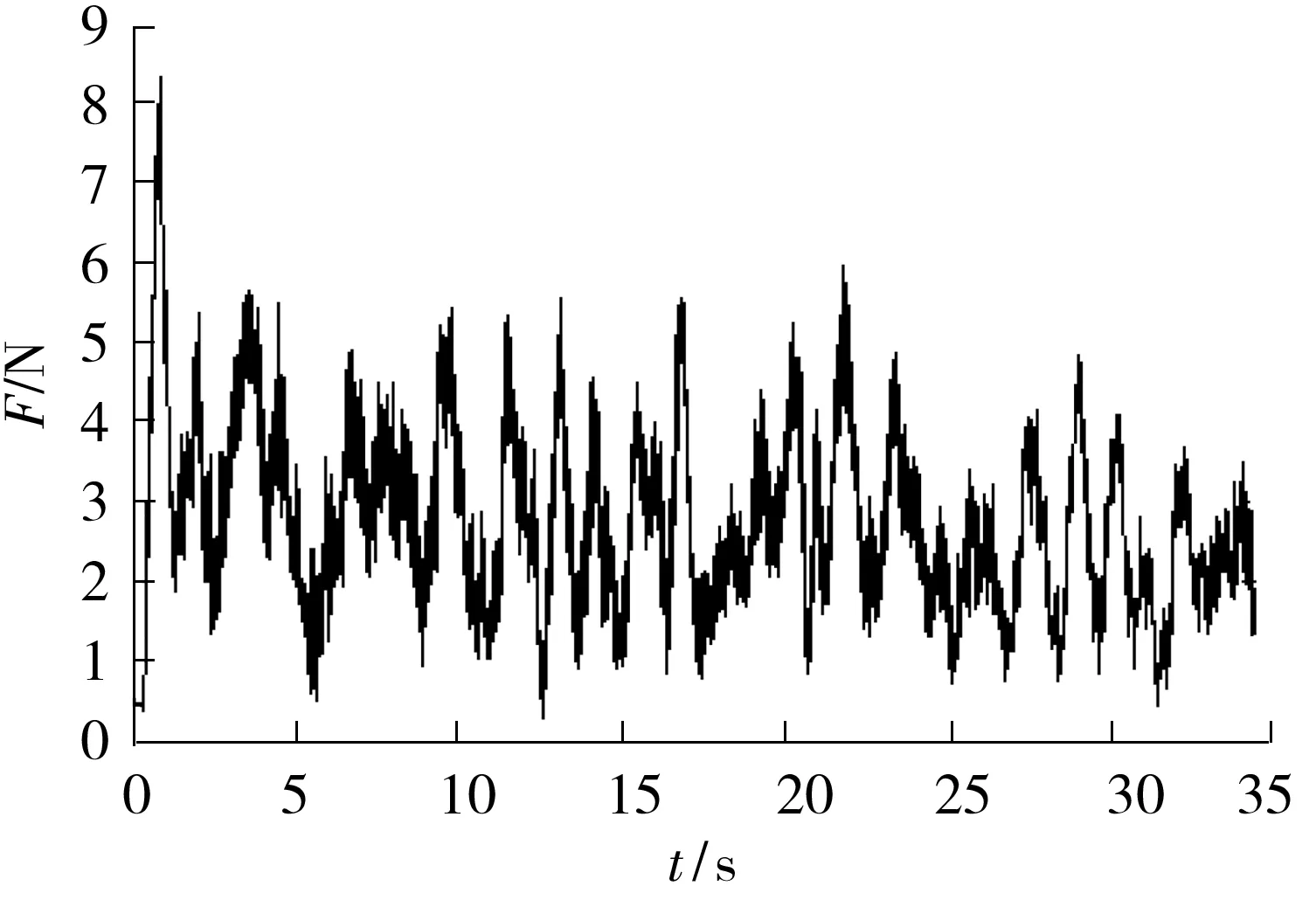
图11 PID控制的切削实验结果

根据前文分析，对PID控制器进行改进，建立基于模糊控制的自适应PID控制器，实时调整切削进给速度，实现切削力平稳控制.其中Tp1、Ti1幅值较大,Td1幅值较小，用于刚性碰撞状态，驱使机器人快速收敛到稳定切削状态，减小震荡周期；Tp2、Ti2、Td2则用于曲率变化较小时的稳定切削状态，确保机器人切削可以保持稳定切削.模糊PID控制的切削实验结果如图12所示.

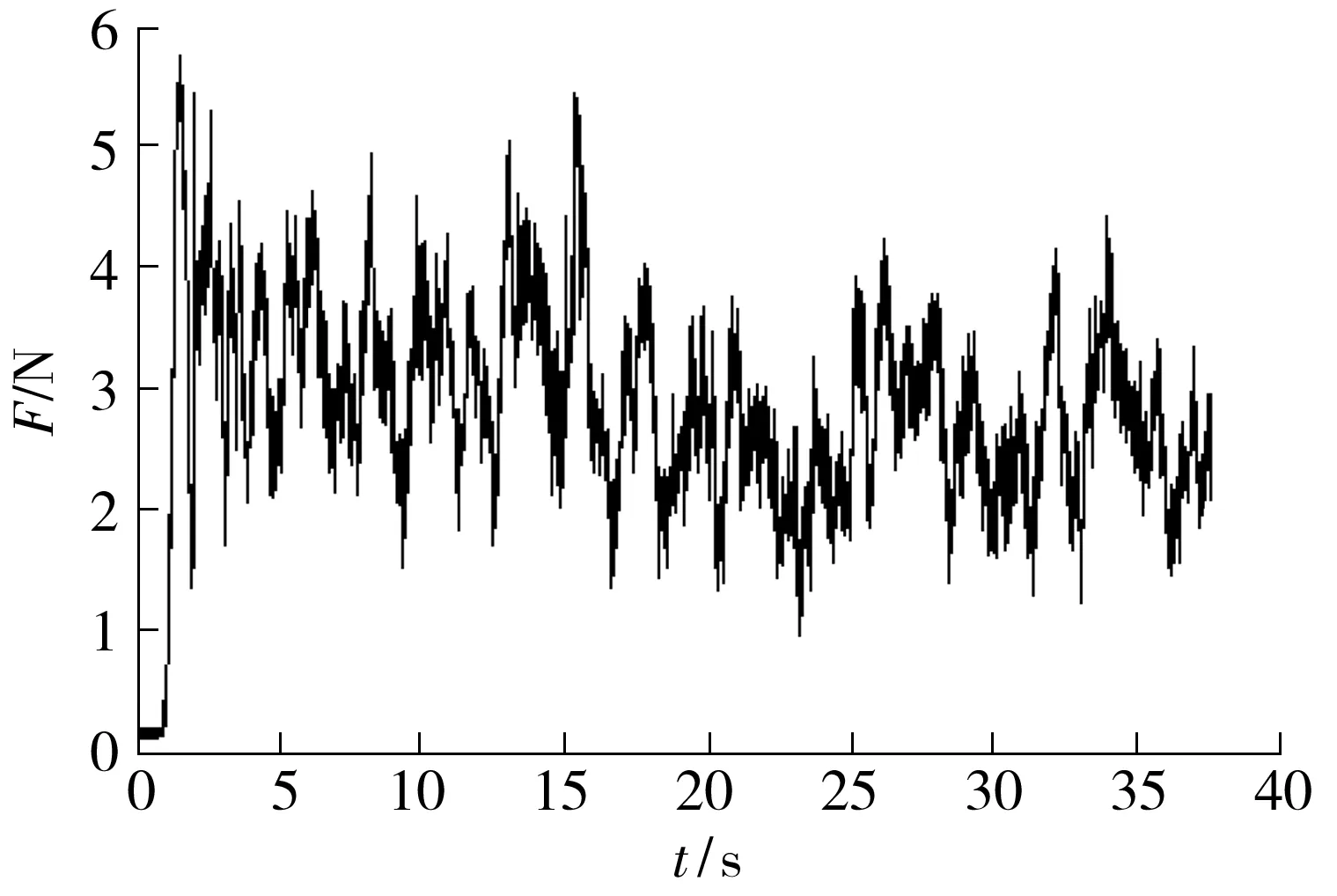
图12 模糊PID控制的切削实验结果

由图12可见，刀具切入工件过程较为平滑，冲击震动影响较小，碰撞状态下的切削力峰值大概为6 N，较开环控制和PID控制大幅减小，这表明模糊PID控制策略能有效减小接触过程中的冲击振动；在随后的稳定切削过程中，力波动幅值在3.5 N左右，平均切削力均值波动在2.6～3.3 N之间，切削过程较为平稳，切削质量得到有效的控制.

实验结果表明，模糊PID控制策略能减小刀具与工件接触过程中的冲击振动，特别是刀具与工件接触瞬间产生的刚性碰撞，与开环控制曲面切削对比，冲击力减小40%，与PID控制对比冲击力减小幅度为20%.同时，模糊PID控制还能有效地抑制曲率变化带来的力波动幅度以及切削力均值变化情况，较开环控制切削减小幅度为30%，较PID控制切削减小幅度为15%，实现了有效的切削力控制.

4 结语

首先分析了机器人切削动态特性，探讨了切削进给速度及刚度对切削状态的影响，并根据切削力波动情况对机器人切削状态进行了分类，分析结果显示，进给速度的改变将影响机器人形变的释放程度，从而对形变引起的加工误差造成影响.随后根据初步实验结果，生成了模糊控制规则，对形变误差、误差变化速度、进给速度进行了模糊度分类，提出了基于模糊PID的曲面切削力控制策略，通过对进给速度的实时调整，对机器人切削力进行控制，从而提高切削质量.通过与开环控制曲面切削、PID曲面切削效果对比，确认了模糊PID曲面切削控制策略的有效性.

由于目前已有的关于机器人切削应用方面的研究主要集中在平面切削和环境刚度辨识方面，较少考虑到机器人刚度和进给速度对切削形变释放的影响，本研究为后续的机器人切削加工应用提供了切削模型和有效的控制方法，并为后续更深入的智能控制方法研究提供了数据支持.

[1] SHOHAM M,LI C J，HACHAM Y,et al.Neural network control of robot arms [J].CIRP Annuals-Manufacturing Technology,1992,41(1):407- 410.

[2] DOMROES F,KREWET C.Application and analysis of force control strategies to deburring and grinding [J].Modern Mechanical Engineering,2013,3(2):11- 18.

[3] JUNG Seul.Experimental studies of neural network impedance force control for robot manipulators [C]∥Proceeding of IEEE Conference on Robotics and Automations.Seoul:IEEE,2011:3453- 3458.

[4] KARAYIANNIDIS Y,DOULGETI Z.Adaptive control of robot contact task with on-line learning of planar surface [J].Automatica,2009,45(10):2374- 2382.

[5] KIGUCHI K,FUKUDA T.Intelligent position/force controller for industrial robot manipulators：application of fuzzy neural networks [J].IEEE Transactions on Industrial Electronics,1997,44(6):753- 761.

[6] 李二超，李炜.在未知环境下面向位控机器人的力/位混合控制 [J].煤炭学报,2007,32(6):657- 660. LI Er-chao,LI Wei.Hybrid force/position control for positional controlled robotic manipulators in unknown environment [J].Journal of China Coal Society,2007,32(6):657- 660.

[7] LIU L,ULRICH B J,ELBESTAWI M A.Robotic grinding force regulation:design,implementation and benefits [C]∥IEEE International Conference on Robotics & Automation.Canada:IEEE,1990:258- 265.

[8] RAFIEIAN F,HAZEL B,LIU Z.Vibro impact dynamics of material removal in a robotic grinding process [J].International Journal of Advanced Manufacturing Technology,2014,73(5/6/7/8):1- 24.

[9] BIGRAS P,LAMBERT M,PERRON C.New optimal formulation for an industrial robot force controller [J].International Journal of Robotics and Automation,2008,23(3):200- 208.

[10] PLIEGO J,ARTEAGA M A.Adaptive position/force control for robot manipulators in contact with a rigid surface with uncertain parameters [J].European Journal of Control,2015,22:1- 12.

[11] 李正义,唐小琦,熊烁,等.沿任意斜面的机器人力/位置控制方法研究 [J].中国机械工程,2012,23(3):304- 309. LI Zheng-yi,TANG Xiao-qi,XIONG Shuo,et al.Study on robot force position control method for arbitrarily inclined plane tracking [J].China Mechanical Engineering,2012,23(3):304- 309.

[12] 任敬心,华定安.磨削原理 [M].北京：电子工业出版社，2011.

[13] 张策.机械动力学 [M].2版.北京：高等教育出版社,2007.

[14] 江守生,汪世益,丁卫,等.数控机床进给系统滚珠丝杠刚度分析 [J].机械工程与自动化，2012(6):88- 89. JIANG Shou-sheng，WANG Shi-Yi，DING Wei,et al.Stiffness analysis of ball screw of NC machine tool feeding system [J].Mechanical Engineering & Automation,2012(6):88- 89.

[15] 梁瑾,罗飞,许玉格.基于决策表的模糊粗糙单调依赖算法及其应用 [J].华南理工大学学报(自然科学版),2011,39(7):7- 12. LIANG Jin，LUO Fei,XU Yu-ge.Fuzzy rough monotone dependence algorithm based on decision table and its application [J].Journal of South China University of Technology(Natural Science Edition),2011,39(7):7- 12.

An Adaptive Force Control Algorithm for Robotic Surface Machining

CHENShou-yanZHANGTie

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,Guangdong, China)

In order to improve the quality of robotic surface machining, deferent robotic machining states are analyzed, and an adaptive force control scheme?is presented. In the investigation, first, the effects of robot stiffness and feed rate on the machining quality are explored, and a machining kinetic model including both impact part and stable grinding part is constructed. Next, a fuzzy PID-based force control model is established according to the relationship between the machining deformation and the feed rate. Then, the machining deformation is calculated according the force feedback, and the machining quality is controlled by adjusting the feed rate in real time. Finally, the proposed method, the open-loop method and the PID control method are compared, and the results show that the fuzzy PID-based surface force control method helps implement high-precision surface machining force control because it can effectively decrease the amplitude of rigid force fluctuation and impact force value.

surface machining; machining quality; feed rate; robotic deformation; fuzzy PID-based force control model

2016- 05- 16

国家科技重大专项项目(20152ZX04005006);广东省科技计划项目(2014B090921004，2015B010918002);广州市产学研协同创新重大专项项目(201505031617224) Foundation items: Supported by the National Science and Technology Major Project of China(20152X04005006) and the Science and Technology Planning Project of Guangdong Province,China(2014B090921004,2015B010918002)

陈首彦(1986-)，男，博士生，主要从事机器人磨削应用研究.E-mail:wabyzhu@hotmail.com

† 通信作者: 张铁(1968-)，男，教授,博士生导师，主要从事工业机器人、服务机器人中的移动机器人的关键技术等研究.E-mail:merobot@scut.edu.cn

1000- 565X(2017)02- 0059- 07

TP 242.2

10.3969/j.issn.1000-565X.2017.02.009