谐波减速器柔轮冷滚工艺及残余应力数值模拟*

吴上生 喻钟鸣

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

谐波减速器柔轮冷滚工艺及残余应力数值模拟*

吴上生 喻钟鸣

(华南理工大学 机械与汽车工程学院， 广东 广州 510640)

针对柔轮工作性能的特殊要求，分析并优化了传统柔轮冷滚压工艺模型，柔轮采用双圆弧齿廓曲线模型；依据修正的Johnson-Cook本构模型建立柔轮冷滚压成形有限元模型并加以验证。仿真结果表明，采用该模型能得到清晰的双圆弧齿形和较均匀的等效应变分布。文中还分析了不同工艺参数(进给速度、滚轮转速及摩擦系数)对柔轮轮齿表面残余应力的影响，结果表明：增大进给速度会降低轮齿表面的残余应力最大值，过大的进给速度会造成“凸起”；适当降低滚轮转速和进给速度，可提高残余应力分布的均匀性；摩擦系数与残余压应力分布深度正相关.

柔轮；冷滚压工艺模型；数值模拟；残余应力；工艺参数

谐波减速器应用于机器人、导弹巡航系统、雷达与航天器等领域，柔轮是谐波减速器核心部件.由于其长期工作在高速及柔性变形条件下，寿命往往仅有1～2年，故其制造工艺是近年来的研究热点.传统柔轮制造工艺(滚、切齿等)效率低下，虽然有人提出了慢走丝线切割加工方法[1]，但该方法对工件装夹定位精度要求很高，加工时间亦较长.冷滚压能极大提高柔轮加工效率.与切削加工相比，滚压过程中金属组织晶粒流线未被割断，使得金属加工表面组织紧致，并产生残余压应力，抑制齿面裂纹产生及扩展[2- 3]，提高了柔轮轮齿的抗疲劳性与寿命.柔轮小模数、多齿数及毛坯材料塑性较好的特性，使滚轮模具使用寿命相对较长，体现了滚压工艺对于柔轮加工的优适性.传统齿轮冷滚压工艺中借助运动补偿强迫控制滚轮与毛坯轴同步，并精确定位滚轮位置；以及通过滚压成形弹塑性变形计算，进而得出进给量修正量，都可以有效提高成形精度[4- 5].

文献[5- 7]提出了谐波齿轮冷轧工艺模型，并研究齿距变化对冷滚压成形精度的影响；朱小星等[8]提出了滚轧齿轮过程中齿廓间相对滑动系数数值模型，采用实验加仿真的方法研究了齿廓间相对滑动对齿廓金属流动方向的影响；Wang等[9]利用DEFORM-3D建立齿轮冷滚有限元模型，分析了成形载荷、应变分布；李泳峄等[10]研究了轴动力增量式花键轴冷滚压过程中分齿精度的影响因素；Reimund、Kamouneh等[11- 12]提出了锥齿轮冷滚压成形的加工硬化预测模型；Kamouneh、吴上生等[13- 14]分析了齿廓间隙及冷滚压机结构对齿轮精密近净成形精度的影响.但截至目前，针对小模数非标齿轮冷滚压成形残余应力分布及影响因素的分析还鲜见报道.本研究采用双圆弧柔轮齿廓；通过约束滚轮初始压入量以提高分齿精度；通过DEFORM-3D软件；对柔轮冷滚压成型过程进行有限元分析，得到柔轮冷滚压过程中的应变分布以及不同工艺参数(进给速度、滚轮转速、摩擦系数)条件下的残余应力分布，为后续的冷滚压柔轮表面残余应力分布控制和加工参数优化提供了参考依据.

1 柔轮冷滚压模型与工艺

1.1 柔轮齿廓建模

柔轮齿形对谐波减速器负载能力及传动精度的影响很大.文中所述柔轮采用双圆弧齿形.圆弧齿形的加工同渐开线齿形一样简易，然而圆弧齿轮的承载能力却优于渐开线齿轮；双圆弧齿形的承载能力较单圆弧提高约40%[15]，其齿廓曲线如图1所示.

图1 柔轮轮齿齿廓曲线

柔轮双圆弧齿形参数方程为：

上圆弧AB段，

Ra=(ρacosα-la)i+sinαj

(1)

下圆弧BC段，

Rr=(lf-ρfcosβ)i+(ρfsinα+bf)j

(2)

齿根过渡圆弧CD段，

(3)

柔轮设计模型如图2所示.

图2 柔轮二维设计模型示意图

除柔轮齿顶圆直径da及齿根圆直径df外，杯壁内径d1与杯壁高h1也是对柔轮设计很重要的参数；杯壁底部有16个直径3.5 mm的沉孔，用于与减速器外壳固连.

柔轮轮齿设计参数如表1所示.

表1 柔轮轮齿设计参数

根据范成法原理，容易得到滚轮模具和柔轮是一对共轭齿廓.建立滚轮三维模型，通过Inventor软件面积计算功能易得柔轮单齿齿廓面积为0.546 96 mm2.根据金属塑性成形体积不变原则计算毛坯尺寸，输入三维软件得模具模型.

1.2 柔轮滚压成形工艺系统

滚压过程中，柔轮毛坯固定在芯轴轴肩上，芯轴一端与机床主驱动轴固连，另一端紧贴顶尖以保证主驱动轴回转刚度.两滚轮模具位于毛坯两侧，三轴线平行且位于同一平面内.两滚轮绕自身轴线做同向、同转速转动，同时通过滚珠丝杆-滑座系统向毛坯轴线方向进给，毛坯轴与滚轮轴反向.滚压工艺原理如图3所示.

图3 柔轮冷滚压工艺过程模型

工艺过程分5个阶段：(1)咬入阶段；(2)分齿阶段，滚轮模具无径向进给运动，相对于毛坯做周向转动；(3)连续进给阶段，滚轮既有径向进给又有周向转动，此过程完成70%的进给量；(4)精整阶段，按一定角速度绕毛坯往复转动；(5)分离阶段.

2 柔轮冷滚压有限元模型及验证

2.1 柔轮冷滚压有限元模型

常用的柔轮材料为30CrMnSiA和40CrNiMoA.文中选用40CrNiMoA，新建材料导入数据库，其力学性能参数如表2所示.材料屈服准则为Von-Mises，本构关系选择式(4)所示的修正的Johnson-Cook模型，相关参数如表3所示.

(4)

表2 40CrNiMoA力学性能参数

表3 修正的Johnson-Cook模型参数

定义毛坯材料为弹塑性体，其余部件为刚体. 为提高计算速度，截取柔轮毛坯1/50模型，设置相应对称面；略去连接法兰部分，只保留杯壁及轮齿.划分得约39 000个元素，对毛坯齿廓部分网格局部细分，网格最小尺寸0.127 mm.由于材料塑性成形总流向约束阻力较小的方向，设置柔轮端面轴向速度约为零，材料只产生周向及径向变形.摩擦系数为0.08(库伦摩擦).模具转速为60 r/min.模具进给量每隔半周就应调整一次，为保证模具首次压入时毛坯分齿的准确性，必须对首次进给量进行约束[16]，计算公式如式(5)所示.

(5)

式中:Z1为柔轮设计齿数；θ为柔轮单齿对应圆心角；r0是毛坯初始外圆半径；l0是毛坯到滚轮的中心距；Ra为滚轮模具的齿顶圆半径.

由式(5)计算得fmin>0.049mm，设置初始压入量为0.1mm.

2.2 有限元模型验证

鉴于柔轮轮齿尺寸特性，传统残余应力测试方法(盲孔法等)已不适用[17].文中采用无损X射线衍射技术测试轮齿表面残余应力分布情况.设备为iXRD便携式X射线残余应力测试分析仪，测量位置为轮齿齿顶圆径向部位.实际加工参数参照有限元模型设置.试验参数为：辐射靶材CuKα，管压25kV，管流4mA，衍射晶面(311)，测试方法为固定法，曝光时间2s，每个衍射角位曝光20次.测试点取相同坐标，采用“点追踪”功能沿径向依次取3点与试验值比较，如表4所示.

表4 仿真值与实测值的对比

试验值比模拟值略大，不同测量深度误差均值约为8.3%.经分析，产生误差的原因可能是：(1)模拟过程中未考虑模具与毛坯接触面摩擦产生的热效应；(2)滚轮径向进给导致其回转中心发生变化.

她结识了很多男男女女。有个妹子骗了别呦呦，说她母亲死了，急需一笔钱，别呦呦把身上的钱都给她了。而妹子拿了钱，再也没回来。

3 数值模拟及分析

3.1 变形分析

图4表示咬入阶段、分齿阶段及连续进给阶段柔轮毛坯等效应变分布云图.可以看出，分齿阶段，齿顶部分有少量“隆起”，这是金属流动造成的；连续进给阶段结束后得到的双圆弧齿形清晰，即实现了柔轮滚压成形的效果.毛坯的变形量和回弹量在实测滚压件中也能得到验证，从另一方面说明了有限元模型的可信度.

3.2 滚压加工参数对残余应力的影响

3.2.1 进给速度的影响规律

总进给量0.350 3 mm，取摩擦系数为0.08，滚轮转速n=60 r/min，进给速度v分别为0.1、0.2、0.3 mm/s时，轮齿表面残余应力分布如图5所示.

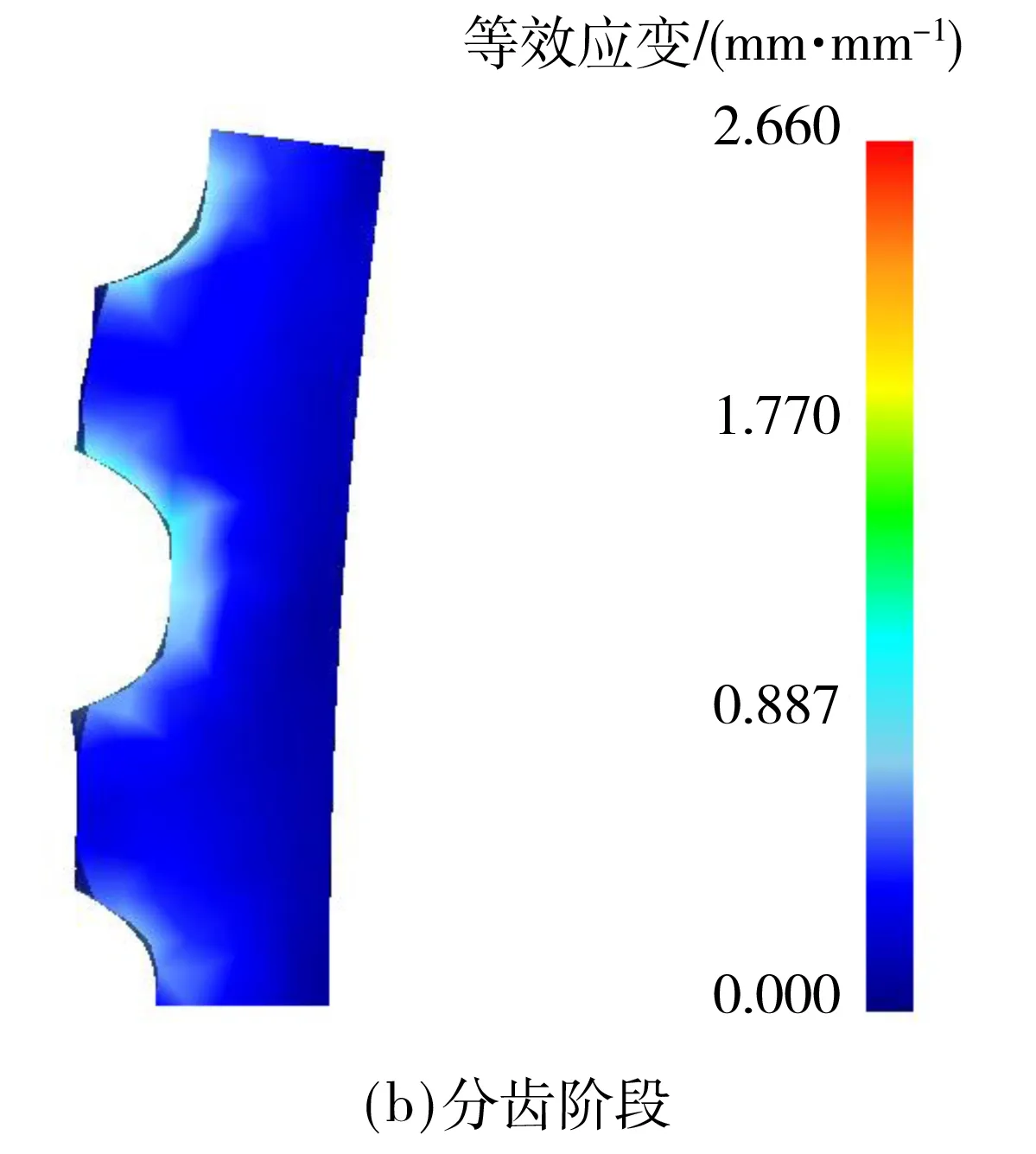
图4 各阶段毛坯等效应变云图Fig.4 Equivalent strain contour of rolling blank at different stages

由图5可知，随进给速度v增大，加工表面残余压应力和残余拉应力的最大值都有所降低；同时，过大的进给速度会使挤压产生的塑性流变作用在接触点形成明显“凸起”，在加工表面产生较大的残余拉应力，致使残余应力分布不均匀，齿面形成弯曲等.

齿根处不同径向深度的残余应力随进给速度的变化曲线如图6所示.

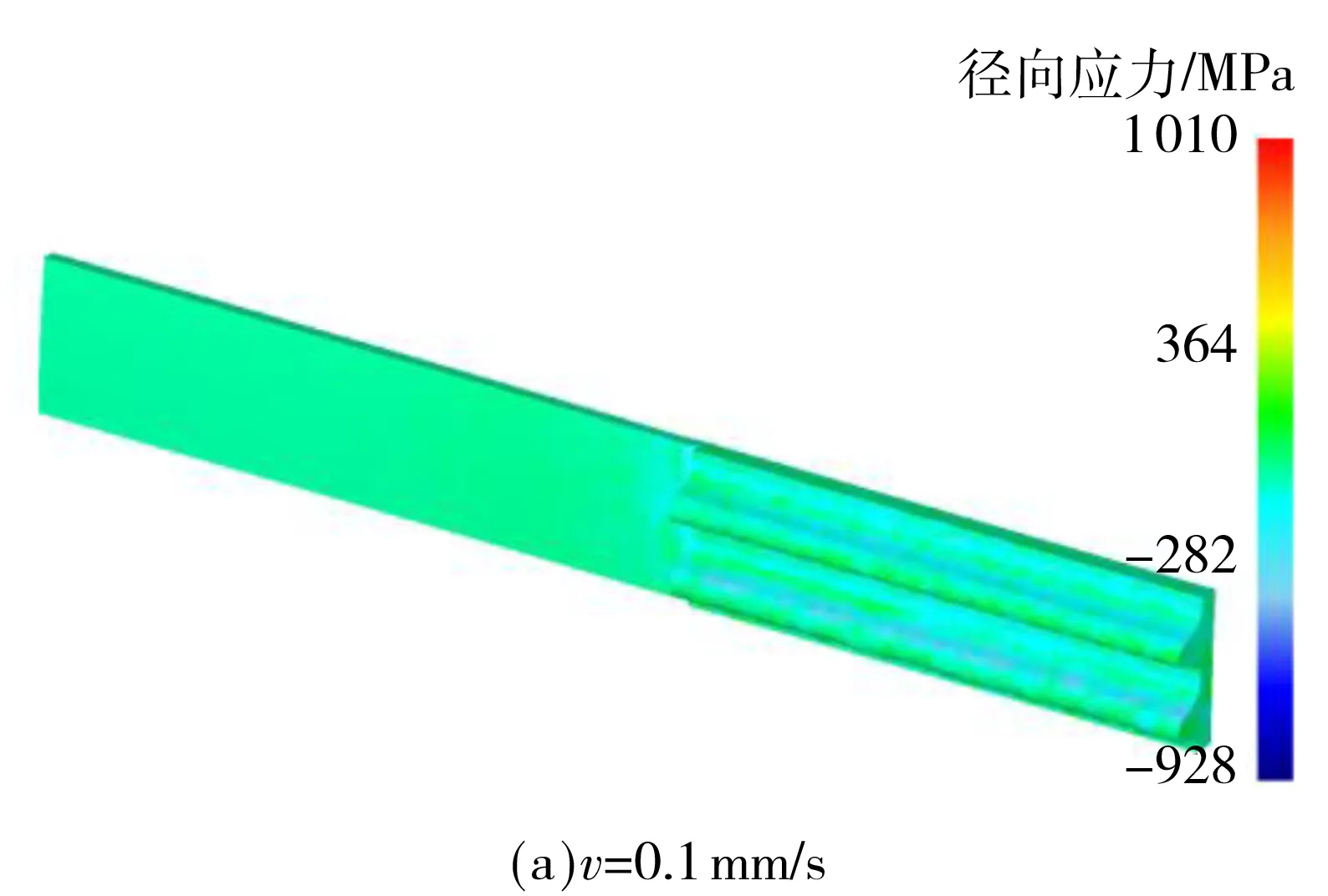
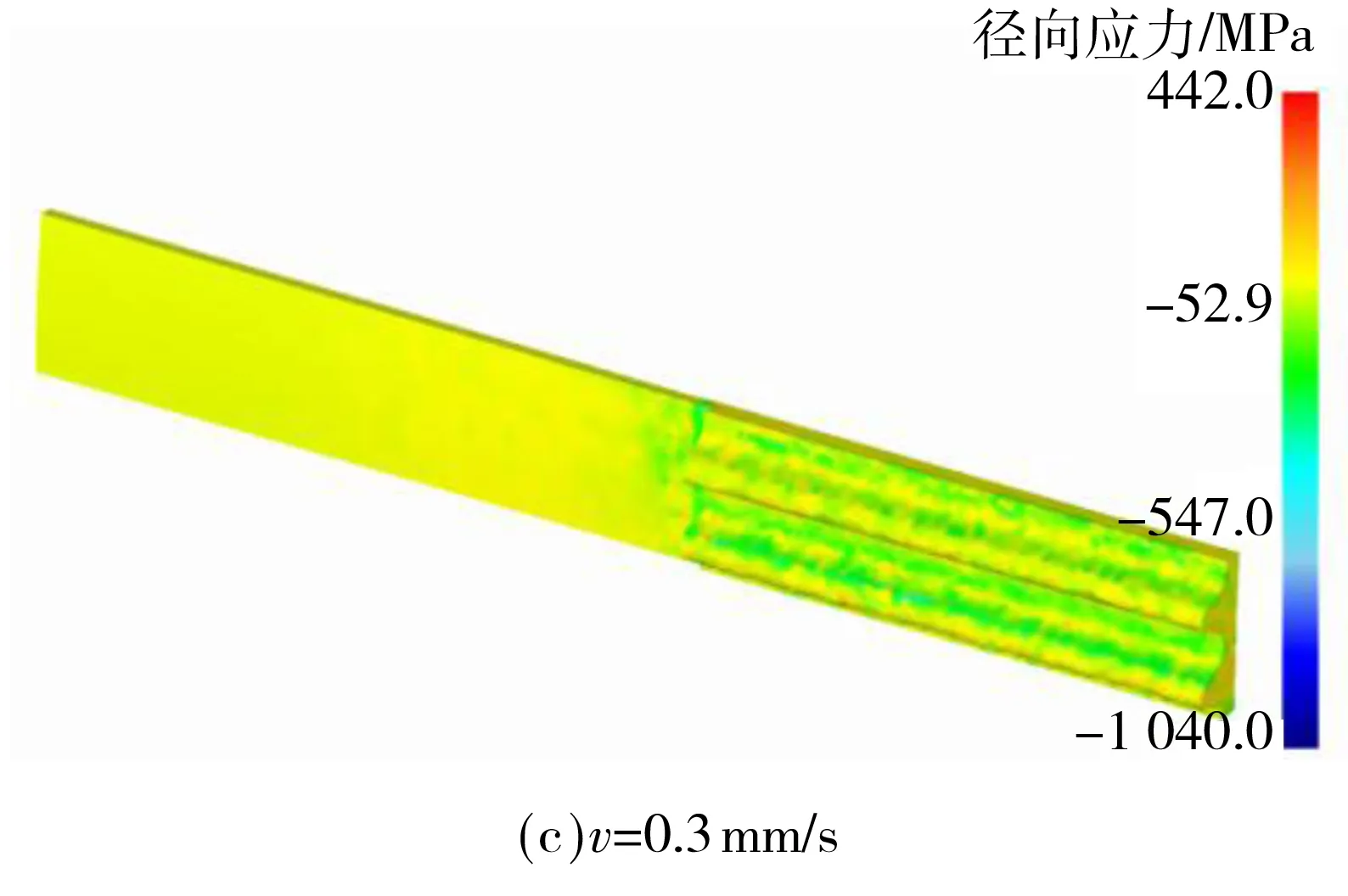
图5 不同进给速度下柔轮表面径向残余应力分布

Fig.5 Surface radial residual stress distribution of flexspline at different feed rates

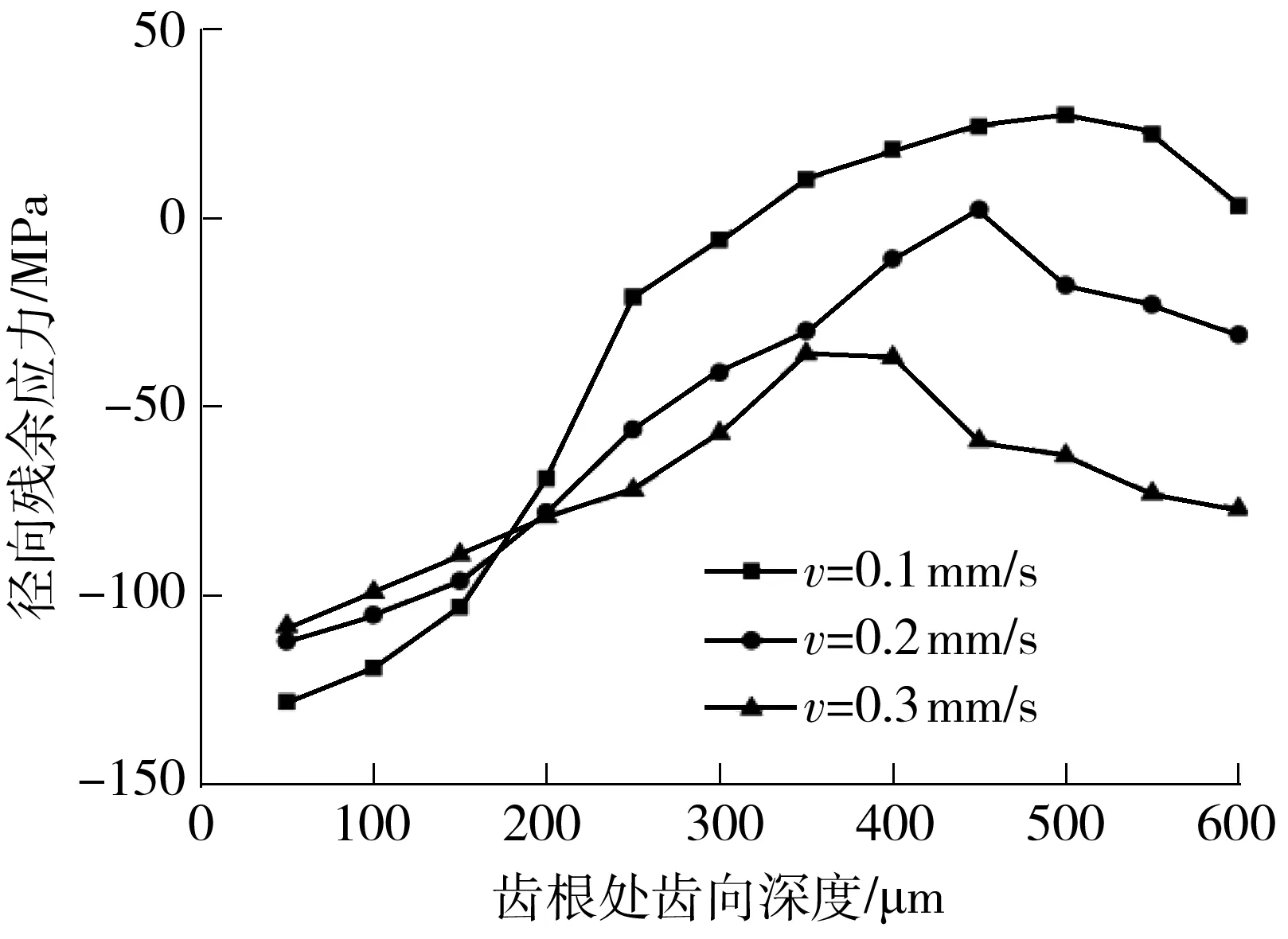
图6 齿根处径向残余应力随进给速度的变化

Fig.6 Radial residual stress of tooth root at different feed rates

齿根处不同周向深度的残余应力随进给速度的变化曲线如图7所示.

图7 齿根处周向残余应力随进给速度变化

Fig.7 Circumferential residual stress of tooth root at different feed rates

齿根处周向残余应力对柔轮工作载荷的抵消作用很大.由图7知，周向残余应力在柔轮齿根处都为压应力，在表面附近呈最大值，并随着周向深度的增大而减小；在进给速度为0.2 mm/s附近呈最大值.

3.2.2 滚轮转速对残余应力分布的影响

选取v=0.1 mm/s，摩擦系数为0.12.滚轮转速n分别取30、45、60 r/min时，柔轮表面径向残余应力分布如图8所示.

由图8知，当进给速度一定时，一定程度增大滚轮转速，相当于增加滚压道次，有利于残余应力均匀性，减少“凸起”点残余拉应力的产生；但是，增大滚轮转速加速滚压成形过程，工件变形区塑性降低，加工硬化程度提高.过高的滚轮转速，不仅会提高金属变形抗力，增加滚压过程的成形力；还会使金属流动阻力增加，工件成形效果不佳.过低的滚轮转速，成形力会很低，相应齿廓接触面正压力降低，可能会产生“打滑”现象.

3.2.3 摩擦系数对柔轮表面径向残余应力分布的影响

选取v=0.1 mm/s，滚轮转速n=60 r/min，摩擦系数分别取0.08、0.12、0.20时，齿顶处径向残余应力、齿根处径向和齿根处周向残余应力分布如图9-11所示.

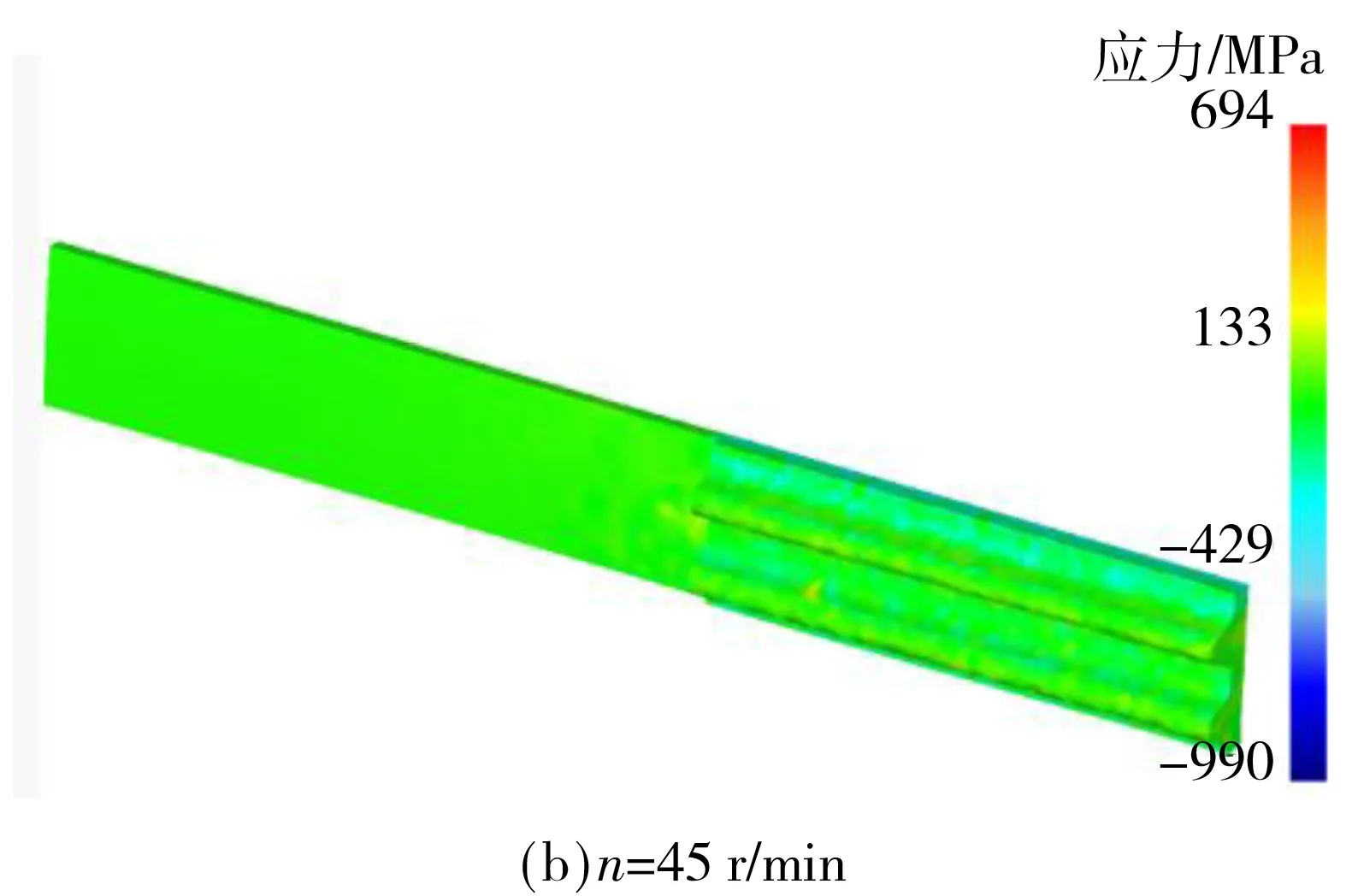
图8 不同滚轮转速下柔轮表面径向残余应力分布

Fig.8 Surface radial residual stress distribution of flexspline at different roller rotational speed

图9 齿顶处径向残余应力随摩擦系数的变化

Fig.9 Radial residual stress of addendum at different friction coefficient

图10 齿根处径向残余应力随摩擦系数变化

Fig.10 Radial residual stress of tooth root at different friction coefficients

图11 齿根处周向残余应力随摩擦系数的变化

Fig.11 Circumferential residual stress of tooth root at different friction coefficient

摩擦系数主要影响加工表面切向残余应力分布.由图9-11知，当摩擦系数较大时，易产生残余压应力；反之，则易产生残余拉应力.当摩擦系数增大时，残余拉应力层越来越远离加工表面.轮齿是在左右两侧齿面挤压作用下形成，两侧加工表面会形成较大残余压应力值.随着摩擦系数增大，残余压应力层深度逐渐增大，最后致使齿顶圆表面附近也形成残余压应力.齿顶圆齿向0.15 mm处开始有残余压应力产生，残余压应力层厚度约为0.45 mm.齿根处径向和周向残余压应力最大值都在表面处.齿根处周向残余压应力值随着摩擦系数增大几乎呈线性增长.轮齿加工表面产生了均匀的周向残余压应力和径向残余压应力，能够抵消柔轮工作载荷下由于轮齿弯曲和摩擦产生的弯曲拉应力.在齿向一定深度下，不同摩擦系数下残余应力值趋于饱和.

综上所述，择优选取v=0.1 mm/s、滚轮转速n=60 r/min、摩擦系数为0.20进行仿真计算，让模具离开毛坯并设置足够长的反应时间.易得柔轮表面等效残余应力最大值663 MPa，此为拉应力.

4 结论

(1)柔轮设计模型采用双圆弧齿廓，通过齿廓法线法设计滚轮模具，计算得到模具初咬入最小进给量为0.1 mm/s，以提高分齿精度.

(2)总进给量0.350 3 mm，当进给速度分别取0.1、0.2、0.3 mm/s时，齿根表面残余拉应力值分别为282、382、547 MPa.过大进给量会产生“凸起”现象，降低残余应力分布均匀性.随着进给量增大，残余压应力与残余拉应力最大值都有所下降；增加滚压次数以及分阶段减小模具进给量，有利于改善齿面残余压应力分布均匀性；增大摩擦系数，提高残余压应力层深度.

(3)从仿真结果来看，滚压成形完成卸去载荷后，轮齿表面等效残余拉应力最大值为663 MPa，远小于材料屈服极限，回弹后不会对柔轮后期工作疲劳特性产生不良影响；而残余压应力能提升柔轮疲劳强度，是有益的.

[1] 吴伟国，于鹏飞，侯月阳.短筒柔轮谐波齿轮传动新设计新工艺与实验 [J].哈尔滨工业大学学报，2014，46(1):40- 46. WU Wei-guo,YU Peng-fei,HOU Yue-yang.New design,new process of harmonic drive with short flexspline and its experiment [J].Journal of Harbin Institute of Technology,2014，46(1):40- 46.

[2] 王生武，温爱玲，邴世君，等.滚压强化的残余应力的数值仿真及工艺分析 [J].计算力学学报，2009，26(1):113- 118. WANG Sheng-wu,WEN Ai-ling,BING Shi-jun,et al.FE simulation of residual stresses by surface rolling and analysis of rolling process [J].Chinese Journal of Computational Mechanics,2009,26(1):113- 118.

[3] 刘福超，雷丽萍，曾攀.滚压有限元模型数值模拟 [J].塑性工程学报，2012,19(2)：17- 21. LIU Fu-chao,LEI Li-ping,ZENG Pan.Surface rolling FE model for numerical simulation [J].Journal of Plasticity Engineering,2012,19(2)：17- 21.

[4] 杨建玺，崔凤奎，王晓强,等.冷滚轧滚轮设计理论及实验修正 [J].中国机械工程，2004，15(24):2168- 2171. YANG Jian-xi,CUI Feng-kui,WANG Xiao-qiang,et al.Design theory and experimental amends of involute spline roller [J].China Mechanical Engineering,2004,15(24):2168- 2171.

[5] 杨向红，林树忠.冷滚轧谐波齿轮分齿精度的影响因素分析 [J].制造业自动化，2011,33(13):65- 68. YANG Xiang-hong,LIN Shu-zhong.Affect factor analyze towards the tooth accuracy of the cold-rolling harmonic gears [J].Manufacturing Automation,2011,33(13):65- 68.

[6] YANG X,LIN S.Factors affecting cold-rolling accuracy of harmonic gears [J].International Conference on Mechanic Automation & Control Engineering,2010：3891- 3894.

[7] 林树忠，袁盛治，玉忠林,等.冷轧谐波齿轮成形工艺及质量分析 [J].燕山大学学报，1986(1):46- 51. LIN Shu-zhong,YUAN Sheng-zhi,YU Zhong-lin,et al.Analysis on the forming process and quality the cold-rolling harmonic gears [J].Journal of Yanshan University,1986(1):46- 51.

[8] 朱小星，王宝雨，杨乐毅,等.齿廓间相对滑动对滚轧齿轮齿廓金属流动的影响 [J].北京科技大学学报，2014，36(2):246- 249. ZHU Xiao-xing,WANG Bao-yu,YANG Le-yi,et al.Effect of relative sliding on tooth profiles metal flow during gear roll forming [J].Journal of University of Science & Technology Beijing,2014,36(2):246- 249.

[9] WANG Zhi-kui,ZHANG Qing.Numerical simulation of involutes spline shaft in cold rolling forming [J].Journal of Central South University of Technology,2010,15(S2):278- 283.

[10] 李泳峄，赵升吨，范淑琴,等.花键轴动力增量式滚轧成形工艺数值分析 [J].材料科学与工艺,2013,21(3)：26- 32. LI Yong-yi,ZHAO Sheng-dun,FAN Shu-qin,et al.Numerical analysis on the power-type incremental rolling forming process of spline shaft [J].Material Science & Technology,2013,21(3)：26- 32.

[11] REIMUND N,DIRK K,UDO H.Description of the interactions during gear rolling as a basis for a method for the prognosis of the attainable quality parameters [J].Production Engineering,2007,1(3):253- 257.

[12] KAMOUNEH A A,NI J,STEPHENSON D,et al.Investigation of work hardening of flat-rolled helical-involute gears through grain-flow analysis,FE-modeling,and strain signature [J].International Journal of Machine Tools & Manufacture,2007,47(7):1285- 1291.

[13] KAMOUNEH A A,NI J,STEPHENSON D,et al.Diagnosis of involute metric issues in flat rolling of external helical gears through the use of finite-element models [J].International Journal of Machine Tools & Manufacture,2007,47(7)：1257- 1262.

[14] 吴上生，黄泽星，陆振威,等.轴向推力滚子激振式振动台设计研究及仿真分析 [J].振动与冲击，2014，33(2)：64- 68. WU Shang-sheng,HUANG Ze-xing,LU Zhen-wei,et al.Design and simulation of axial thrust roller-exciting vibration table [J].Journal of Vibration and Shock,2014，33(2)：64- 68.

[15] 辛洪兵.双圆弧谐波齿轮传动基本齿廓设计 [J].中国机械工程，2001，22(6)：656- 662. XIN Hong-bing.Design for basic rack of harmonic drive with double-circular-arc tooth profile [J].Chinese Journal of Mechanical Engineering,2001，22(6)：656- 662.

[16] 于杰,王宝雨,胡正寰.齿轮轴齿形轧制成形的模具设计与实验 [J].北京科技大学学报，2011，33(12)：1544- 1549. YU Jie,WANG Bao-yu,HU Zheng-huan.Die design and experiment for forming the teeth of shafts by rolling [J].Journal of University of Science and Technology Beijing,2011，33(12)：1544- 1549.

[17] 张霞.无损应力测试在17Cr2Ni2Mo钢汽车齿轮中的应用 [J].热加工工艺,2016(4)：243- 244. ZHANG Xia.Application of non-destructive stress mea-surement in 17Cr2Ni2Mo steel automobile gear [J].Hot Working Technology,2016(4)：243- 244.

Cold Rolling Process and Numerical Simulation of Residual Stress for Flexspline of Harmonic Reducer

WUShang-shengYUZhong-ming

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640,Guangdong,China)

By taking into consideration the special requirements for function and property of flexspline, the traditional cold rolling process model is analyzed and optimized based on the double-circle-arc model for flexspline. Then, a finite element model describing the cold rolling process is established according to the modified Johnson-Cook constitutive model and is finally verified. Simulated results show that, with the help of the established model, clear double-circle-arc tooth profile and uniform equivalent strain distribution can both be obtained. Moreover, by analyzing the influences of such parameters as feed rate, roller’s rotation rate and friction coefficient on the residual stress distribution on gear tooth surface, it is found that (1) increasing the feed rate may reduce the maximum residual stress on tooth surface, but excessive feed rate may result in “bulge” on the surface; (2) properly reducing the rotation speed and feed rate of the roller may improve the uniformity of residual stress distribution; and (3) the friction coefficient positively correlates with the distribution depth of residual compressive stress.

flexspline;cold-rolling process model;numerical simulation;residual stress;process parameter

2016- 05- 29

广东省科技计划项目(201605131317517) Foundation item: Supported by the Guangdong Province Science and Technology Planning Project(201605131317517)

吴上生(1963-)，男，博士，教授，主要从事机械装备自动控制理论与应用研究. E-mail:shshwu@scut.edu.cn

1000- 565X(2017)02- 0052- 07

TG 306

10.3969/j.issn.1000-565X.2017.02.008