3,5,6-三氯-2-吡啶醇在紫色土中的吸附特征与参数估计

雷文娟 霍 喜 周向阳

(1.四川大学建筑与环境学院， 成都 610065； 2.四川大学水力学与山区河流开发保护国家重点实验室， 成都 610065)

3,5,6-三氯-2-吡啶醇在紫色土中的吸附特征与参数估计

雷文娟1霍 喜1周向阳2

(1.四川大学建筑与环境学院， 成都 610065； 2.四川大学水力学与山区河流开发保护国家重点实验室， 成都 610065)

通过批量平衡实验和土柱实验获得了3,5,6-三氯-2-吡啶醇(简称TCP)在紫色土土壤中的吸附特征，并应用模型对上述吸附过程进行模拟。其中，吸附动力学参数通过准一阶、准二阶动力学方程、Elovich模型和粒子扩散模型反演；等温吸附参数应用Freundlic、Langmuir和Linear模型反演；土柱实验中的吸附参数基于Thomas与Yoon-Nelson模型反演。结果表明：TCP在紫色土中的吸附动力学过程包含快速的表面物理吸附和慢速的内部化学扩散2个阶段，且粒子扩散模型表现最好。等温吸附过程可以通过Freundlic模型描述(R2=0.94)，获得的吸附容量常数Kf为0.79 mL/g，吸附水平较小说明TCP在紫色土中具有较大的迁移风险。TCP在土柱中达到平衡需要的时间约为1 215 min，土壤对TCP的吸附率为10.65%。Thomas与Yoon-Nelson模型能够较好地模拟TCP在紫色土中的动态吸附曲线(R2≥0.84)，获得的平衡浓度q0为0.008 6 mg/g。

3,5,6-三氯-2-吡啶醇； 紫色土； 吸附实验； 吸附模型

引言

3,5,6-三氯-2-吡啶醇(3,5,6-trichloro-2-pyridinol，简称TCP)是杀虫剂毒死蜱和除草剂绿草定的主要降解产物[1-3]，分布于土壤、水体、空气和生物体内，并且作为合成上述农药的中间体化合物，被排入生产地附近水体中，进而污染环境[4]。TCP 的水溶性较大(45 mg/L)，与土壤、沉积物等结合能力相对较弱，抗降解能力较强，能够在环境中长期存在，更易迁移，且毒性与其母体相当，对土壤和水体环境污染较大[5-8]。因此，美国环保局将TCP归类为持久性、易于迁移性物质[9]。

尽管TCP在土壤中的迁移性较强，但其在土壤中的吸附行为同样不容忽视，这对于掌握易迁移类污染物在土壤中的吸附特征、揭示其在环境中的归趋和评价污染物在土壤中风险具有重要的意义。针对土壤对污染物的吸附行为特征，主要采用两类方法进行研究。一类是批量平衡法，包括等温吸附和吸附动力学方法。该方法因简单易行而被广泛应用，但不足是实验条件相对理想化。另一类是穿透曲线方法(Breakthrough curve, BTC)。该方法以土柱出流液的相对浓度C/C0与实验运行时间t(或者体积)绘制穿透曲线，通过计算穿透曲线获得的参数来表征污染物的吸附动力学行为。穿透曲线中的吸附行为和田间的环境更相似，它反映了流动相与固定相之间的吸附平衡关系、吸附动力学和传质机理[10-11]，因而该方法在污水处理方面应用较广泛[12-14]，但相对于前者穿透曲线实验更费时。

紫色土是长江上游地区的主要耕作土壤，但少有研究探讨农药或其降解产物在其中的吸附与迁移情况，并且研究农药等污染物在土壤中的吸附大多仅限于等温吸附和吸附动力学方法。因此，本文以TCP为目标污染物，以典型紫色土耕作土壤为研究对象，通过等温吸附实验、吸附动力学实验和土柱实验3种方法来分别探索TCP在理想条件和接近自然条件下的吸附特征；并分别应用多种模型对不同条件下的吸附数据进行参数反演。其中，吸附动力学参数通过准一阶、准二阶动力学方程、Elovich模型和粒子扩散模型反演[15-22]，等温吸附参数应用Freundlic、Langmuir和Linear模型反演，土柱实验中的吸附参数基于Thomas和Yoon-Nelson模型反演[23-25]。以揭示TCP在不同环境下的吸附特征，优选吸附模型并反演吸附参数，为掌握TCP在紫色土土壤中的迁移机理提供理论和实验依据，同时为研究该区域的较强迁移性污染物的环境行为提供参考。

1 材料与方法

1.1 实验土壤

土壤样品选取长江上游区域典型坡耕地土壤，其基本性质是：大孔隙发育良好，有机质含量低，饱和导水率高，团粒结构水稳性差，颗粒分散性强，水土流失问题突出且污染物易于发生迁移[26-27]。采样地点位于四川省中江县南部，如图1所示。土壤风干过2 mm筛，测定土壤的基本理化性质，结果如表1所示。

图1 采样点地理位置及区域DEM图Fig.1 Location of sampling site and regional DEM

表1 实验土壤基本性质Tab.1 Physical and chemical properties of purple soil

1.2 吸附实验方法

1.2.1 批量平衡实验

等温吸附实验方法：称取过100目筛风干土样5 g置于30 mL玻璃离心管中，按水土质量比1∶1加入5 mL一定浓度的TCP溶液(浓度梯度为0、2、4、6、8、10 mg/L，溶液用0.01 mol/L CaCl2配置，含质量分数为0.05%的NaN3)，密封后在室温条件下振荡24 h，样品于3 400 r/min下离心10 min，上清液用于检测。

吸附动力学实验方法：实验方法同1.2.1节，其中TCP初始浓度为4 mg/L，土样为5 g。密封后在室温下振荡，定时(10 min、30 min、1 h、2 h、4 h、6 h、8 h、12 h、24 h)取样测试。以上实验均设2个平行样，结果取均值进行计算。

1.2.2 土柱实验

土柱实验装置由玻璃土柱(长10 cm、内径4.4 cm)、蠕动泵和部分收集器构成(图2)。将过100目筛后的土壤按照测定的容重分层填装成柱。实验过程中以容量瓶和BT100-1F 型蠕动泵(保定兰格恒流泵有限公司)作为供水装置，土柱垂直放置，土柱上、下端用石英砂作为反滤层。入渗溶液为10 mg/L TCP、0.05% NaN3和0.01 mol CaCl2的混合溶液，流速为0.15 mL/min，土柱下端出流液采用CBS-A 程控全自动部分收集器(上海泸西分析仪器厂有限公司)定时采集，直至土柱出流中的TCP 浓度不变时，视为达到平衡，实验结束，样品待测。实验设2个平行，重复性较好，结果取均值进行计算。

图2 土柱实验示意图Fig.2 Schematic of soil column experiments1.储液瓶 2.蠕动泵 3.土柱 4.部分收集器

1.3 检测方法

实验结束后，TCP浓度采用高效液相色谱仪进行测定[28]。仪器配有四元泵、紫外检测器(UV)、自动进样器，色谱柱为Eclipse plus C18, 4.6 mm×150 mm(5 μm)。流动相(甲醇与水体积比为85∶15，水相中加入体积比为0.02%的乙酸)，等梯度洗脱，流速为1.0 mL/min，进样体积10 μL，柱温30℃，紫外检测波长293 nm。

1.4 数据处理

TCP的吸附量计算公式为

(1)

式中C0——溶质的初始浓度，mg/LCe——溶质的平衡浓度，mg/LV——溶液体积，mLm——土壤质量，g

1.4.1 吸附动力学模型

吸附动力学实验结果用准一阶动力学方程、准二阶动力学方程、Elovich模型和粒子扩散模型进行模拟。其中准一阶、准二阶动力学方程分别为

(2)

(3)

式中qe——平衡时刻的吸附容量，mg/gqt——t时刻的吸附容量，mg/gt——接触时间，hk1——准一阶速率系数，h-1k2——准二阶速率系数，g/(mg·h)

Elovich方程通常用于气态以及液态吸附系统，计算公式为

qt=βlnα+βlnt

(4)

式中α——Elovich方程的初始吸附速率常数,mg/(g·h)

β——与表明覆盖度和活化能有关的常数，g/mg

粒子扩散模型在吸附过程中用来确定限制速率。如果qt与t0.5的相关关系绘制为直线，表明吸附主要是由粒子扩散来实现速率限制，否则会有其他的吸附因素来影响整个过程。模型为

qt=kidt0.5+a

(5)

式中kid——粒子扩散速率常数，mg/(g·h0.5)

a——常数，mg/g

1.4.2 等温吸附模型

TCP的等温吸附参数采用Freundlic、Langmuir和Linear模型进行拟合，模型分别为

(6)

(7)

qe=KdCe

(8)

式中Kf——Freundlic吸附容量，mL/gn——Freundlic吸附强度qm——最大吸附容量，mg/gb——与吸附能相关的Langmuir常数，L/mgKd——吸附常数，mL/g

1.4.3 土柱实验模型

在土柱实验中，土壤对TCP总的吸附量通过计算穿透曲线的闭合区面积获得，计算公式[14]为

(9)

式中ttotal——总流动时间，minCads——t时刻吸附的溶质浓度，mg/LF——流速，mL/minA——穿透曲线的面积，cm2

平衡吸附总量qe(exp)为土壤单位质量上吸附的TCP的质量(mg/g)，可表示为

(10)

式中M——土柱中土壤的总质量，g

进入到土柱中的TCP的总量(mtotal)可表示为

(11)

式中C0——TCP的初始浓度，mg/L

吸附率(%)为

(12)

总的体积Veff(mL)为

Veff=Fttotal

(13)

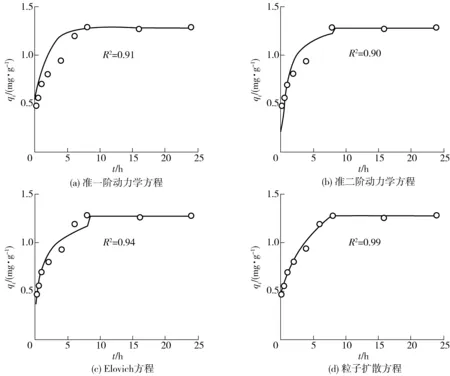
图3 TCP在紫色土土壤中的吸附动力学及模拟结果Fig.3 TCP adsorption kinetics onto purple soils and fitted curves

实验数据用Thomas与Yoon-Nelson经验模型来确定污染物的反应行为和参数，并用来解释其在土柱实验中的吸附动力过程。Thomas模型是研究柱状吸附床的吸附动力学模型[24]。模型假定遵从Langmuir动力学吸附-解吸，并且忽略柱子中的沿轴扩散吸附[29-32]，模型表达式为

(14)

式中Ct——t时刻的TCP浓度，mg/LkTH——Thomas速率常数，mL/(min·mg)q0——吸附容量，mg/g

Yoon-Nelson模型相对简单，对吸附剂的特征、种类和吸附床的物理特征没有限制[25]，其表达式为

(15)

式中kYN——Yoon-Nelson模型速率常数，min-1τ——吸附50%吸附质所需时间，min

2 结果与分析

2.1 批量平衡实验结果分析

2.1.1 吸附动力学分析

TCP在紫色土中的动力学吸附曲线如图3所示。可以看出，TCP在0～10 h之间为快速吸附，在接近10 h时进入吸附平衡的慢吸附阶段，吸附率为32.5%。吸附动力学模型和吸附过程中的参数对预测吸附效率是非常有用的，图3显示了准一阶动力学方程、准二阶动力学方程、Elovich和粒子扩散模型模拟的TCP在土壤中的吸附动力学过程，并获得了吸附参数(表2)。4个模型均能较好地模拟TCP在紫色土中的吸附动力学过程(R2≥0.90)。但在快速吸附阶段(0～10 h)，准一阶和准二阶动力学方程不能很好地描述TCP在紫色土中的吸附动力学。

表2 TCP在土壤中的吸附动力学模拟参数Tab.2 Parameters of TCP estimated by adsorption kinetics models

其中，粒子扩散模型模拟效果最好(R2≥0.99)，并且qt与t0.5呈现比较好的线性关系，说明TCP在紫色土中的动力学吸附过程中主要受粒子的内部扩散作用。并且在吸附的初始阶段发生了表面吸附；随着吸附的进行，kid不断增加，但吸附速率却不断降低，说明内扩散限制开始起作用。而准一阶动力学模型拟合的R2小于粒子扩散模型，这说明相比内部扩散，外部传质对吸附过程的控制作用不明显。准二阶动力学模型中，速度控制是化学吸附，动力学模型基于Langmuir 吸附等温方程。模型拟合的R2较其他模型小，但也说明TCP在吸附过程中，受多种因素控制。Elovich模型能较好地描述实验数据，这是因为在快速吸附阶段，吸附剂的表面覆盖率较小，吸附主要由表面扩散决定[33]。

上述模型的模拟结果说明 TCP在紫色土中的吸附包含了吸附的所有过程，如表面吸附和颗粒内部扩散等；吸附过程不是简单的快速吸附，而是包含了快速的表面物理吸附和慢速的内部化学扩散2个阶段。

2.1.2 等温吸附

等温吸附模型通过描述qe与Ce的关系来确定污染物的吸附机理。采用Freundlic、Langmuir和Linear吸附模型对TCP在紫色土中的等温吸附曲线进行拟合，结果如图4所示，并获得相关的吸附参数(表3)。可以看出，Freundlic模型相较其他模型能够更好地模拟TCP在紫色土中的吸附过程(R2=0.94)。同时，Langmuir和Linear吸附模型也能够较好地模拟TCP的吸附过程(R2≥0.90)。Freundlic模型中的n表示吸附强度，大于1.0说明不利于吸附[34]。本研究中拟合的n为2.40，表明TCP在紫色土土壤中不利于吸附，Kf为0.79 mL/g。Langmuir模型拟合TCP在紫色土土壤中的最大单层吸附容量qm为2.54 mg/g。Linear模型拟合的Kd为0.16 mL/g，处于较小的吸附水平。Freundlic和Linear模型拟合的参数与孙宝利[4]研究TCP在紫色土中的等温吸附结果较接近，分别为1.37、0.5 mL/g。同时也说明TCP在紫色土中具有很大的迁移风险。

图4 TCP在土壤中的等温吸附曲线及模拟结果Fig.4 TCP adsorption isotherms onto purple soil and fitted curves

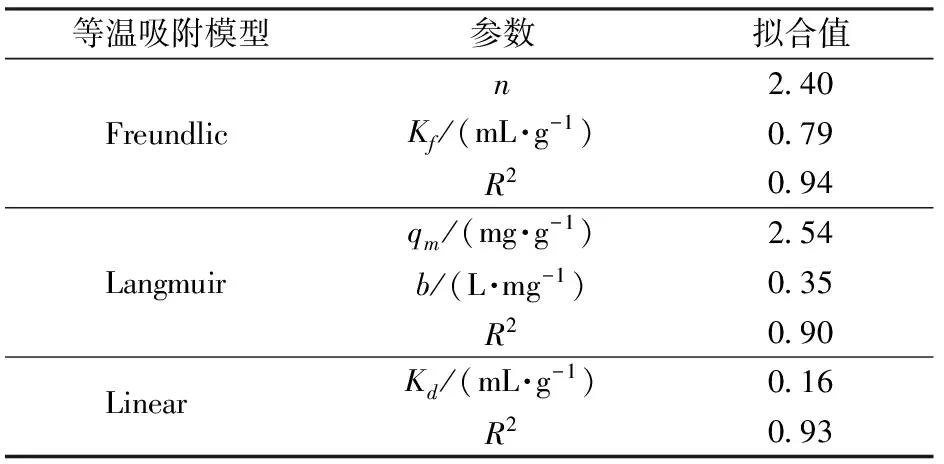
表3 TCP在土壤中的等温吸附曲线拟合参数Tab.3 Parameters of TCP estimated by adsorption isotherms models

2.2 土柱实验结果分析

TCP在紫色土土柱中的穿透曲线如图5所示。可以看出，在500 min之前只有极少的TCP存在，随着吸附时间的延长，上层土壤吸附容量趋于饱和，吸附区向下移动。当吸附区到达土柱底端时，出流液中TCP浓度逐渐增大，直至达到平衡，约为初始浓度的90%。依据穿透曲线的数据，按照式(9)～(13)计算的参数如表4所示。基于图5和表4可知，TCP在土柱中达到平衡需要的时间约为1 215 min，平衡浓度为0.001 3 mg/g，土壤对TCP的吸附率为10.65%，处于较小的水平，这与等温吸附结果一致。

图5 TCP在土柱中的穿透曲线Fig.5 TCP breakthrough curve in soil column

TCP在紫色土土柱中的穿透曲线分别用Thomas与Yoon-Nelson模型来模拟并获得相应的吸附参数，如表5所示。Thomas与Yoon-Nelson模型均能较好地模拟TCP在土柱中的穿透曲线(R2≥0.84)。根据Thomas模型的模拟结果，参数q0为0.008 6 mg/g，较实测数据略大(0.001 3 mg/g)；Thomas吸附常数kTH为0.006 2 mL/(mg·min)，处于较小水平，同时也说明TCP在土柱中的动态吸附是一个吸附位点，一旦被吸附质占据后则吸附不再发生，而且轴向扩散弱[11]。依据Yoon-Nelson模型的模拟结果，吸附50%TCP所需时间为877.44 min，比实测值对应的时间小(960 min)；获得的平衡吸附量q0与Thomas模型的一致，为0.008 6 mg/g；Yoon-Nelson模型速率常数kYN为0.006 2 min-1。按照上述实验结果与模拟分析，虽然Thomas和Yoon-Nelson模型获得的参数值与实测值存在误差，但在可接受的误差范围内，说明2个模型能够用来预测TCP在紫色土土壤中的穿透曲线。

表4 TCP在土柱实验中吸附参数Tab.4 Parameters calculated by TCP breakthrough curve in soil column

表5 TCP Thomas和Yoon-Nelson模型模拟TCP在土柱中的穿透曲线参数Tab.5 Parameters of TCP breakthrough curve estimated by Thomas and Yoon-Nelson models

3 结论

(1)吸附动力学过程中，粒子扩散模型模拟效果最好(R2=0.99)，吸附量qt与时间t0.5呈良好的线性关系，说明粒子扩散作用对TCP在紫色土壤中的动力学吸附过程有重要影响。准一阶动力学方程、准二阶动力学方程、Elovich和粒子扩散模型均能较好地模拟TCP在土壤中的吸附动力学过程(R2≥0.90)，反映出TCP在紫色土中的吸附包含了快速的表面物理吸附和慢速的内部化学扩散2个阶段。

(2)等温吸附过程中，Freundlic、Langmuir和Linear吸附模型能够较好地对TCP在紫色土中的等温吸附曲线进行模拟(R2≥0.90)，其中Freundlic模型表现最好(R2=0.94)。反演所得的吸附容量常数Kf为0.79 mL/g，较小的Kf值表明TCP在紫色土壤中有较大的迁移风险。

(3)土柱实验吸附过程中，Thomas和Yoon-Nelson模型能够对TCP在紫色土土柱中的吸附过程进行较好的模拟(R2≥0.84)，获得的单位土壤质量平衡吸附量为0.008 6 mg/g，吸附速率为0.006 2 min-1。

1 CHAPMAN R, HARRIS C R. Persistence of chlorpyrifos in a mineral and organic soil [J]. Environment Science Health, Part B, 1980, 15(1): 39-46.

2 RACKE K D, COATS J R, TITUS K R. Degradation of chlorpyrifos and its hydrolysis product 3,5,6-trichloro-2-pyridinol in soil [J]. Journal of Environment Science Health, Part B, 1988, 23(6): 527-539.

3 YANG H, WU X, ZHOU L X. Effect of dissolved organic matter on chlorotoluron sorption and desorption in soils [J]. Pedosphere, 2005, 15(4): 432-439.

4 孙宝利. 毒死蜱主要有毒代谢物3,5,6-TCP 在土壤中的环境行为研究[D]. 北京：中国农业科学院, 2011. SUN B L. Study on the soil environment behavior of the chlorpyrifos relevant-metabolite 3,5,6-TCP [D]. Beijing: Chinese Academy of Agricultural Sciences, 2011. (in Chinese)

5 FENG Y. Transformation of 3,5,6-trichloro-2-pyridinol, a metabolite of pyridine e-based pesticides[D]. Pennsylvania: The Pennsylvania State University, 1995.

6 FENG Y, RACKE K D, BOLLAG J M. Use of immobilized bacteria to treat industrial wastewater containing a chlorinated pyridinol [J]. Applied Microbiology and Biotechnology, 1997, 47(1):73-77.

7 RACKE K D, ROBBINS S T. Factors affecting the degradation of 3,5,6-trichloro-2-pyridinol in soil [M]∥ACS Symposium Series, 1991,459: 93-107.

8 ARMBRUST K L. Chlorothalonil and chlorpyrifos degradation products in golf course leachate [J]. Pest Management Science, 2001, 57(9): 797-802.

9 叶振华. 化工吸附分离过程[M]. 北京: 中国石油化工出版社, 1992.

Adsorption Characteristics and Its Parameters Estimation of 3,5,6-trichloro-2-pyridinol in Purple Soil

LEI Wenjuan1HUO Xi1ZHOU Xiangyang2
(1.CollegeofArchitectureandEnvironment,SichuanUniversity,Chengdu610065,China2.StateKeyLaboratoryofHydraulicsandMountainRiverEngineering,SichuanUniversity,Chengdu610065,China)

The adsorption parameters of pesticide are one of the most important factors to determine its destination and pollution in the soil and water. However, these parameters varied substantially in different environments even though tested by the same soil samples. 3,5,6-trichloro-2-pyrdionl (TCP) is the main degradation product of pesticide chlorpyrifos and herbicide triclopyr, and it exhibits anti-degradation ability, high water solubility and high migration capability, which would lead to the soil and water pollution easily. This situation might be exacerbated in purple soil distributing regions because of the low organic matter content and large pores with high water conductivity of the soil. In order to provide more accurate data, the adsorption behaviors of TCP in purple soil were explored on the basis of three environments: isothermal adsorption and kinetic adsorption by bath equilibrium experiment, and soil column experiment by breakthrough curves. Then the parameters of these adsorption processes were simulated by their corresponding models. As for kinetic adsorption, the performance of four models was tested, which were pseudo-first-order, pseudo-second-order, Elovich, and intraparticle diffusion model, respectively; isothermal adsorption was fitted by Freundlic, Langmuir and Linear models; and the adsorption in soil column experiment was simulated by Thomas and Yoon-Nelson models. By comparing the performance of these methods, the appropriate models were identified, and the adsorption parameters in different environments were obtained through inversion simulation. The main conclusions were as follows: the kinetic adsorption of TCP in purple soil included two stages: both rapid physical adsorption on the surface and slow chemical diffusion inside, and intraparticle diffusion model performed the best with determination coefficientR2of 0.99, implying the diffusion had important effect on the kinetic adsorption; as for isothermal adsorption, Freundilic model performed the best (withR2of 0.94), and the inversion simulated parameter ofKfwas 0.79 mL/g, which indicated a high risk of transportation in soil; in the soil column experiment, the equilibrium time was 1 215 min for breakthrough curve of TCP, and the adsorption rate was 10.65%. The dynamic adsorption curves can be well simulated by Thomas and Yoon-Nelson models (R2≥0.84), from which the equilibrium concentration was obtained:q0equaled to 0.008 6 mg/g. Therefore, this study identified the appropriate model to describe the adsorptions of TCP in purple soil in different environments, and the corresponding parameters were obtained by inversion simulation. These results were able to provide useful references for predicting the destination of TCP in purple soil, as well as other easy transporting pollutants.

3,5,6-trichloro-2-pyridinol; purple soil; adsorption experiment; adsorption models

2016-08-18

2016-10-30

中国博士后科学基金项目(2016M592671)

雷文娟(1984—)，女，讲师，博士，主要从事污染水文学研究，E-mail: leiwenjuan@scu.edu.cn

10.6041/j.issn.1000-1298.2017.05.033

TS201; S375

A

1000-1298(2017)05-0267-08