胶乳分离机高速转鼓流体动力学特性

薛晓宁，石 凯

胶乳分离机高速转鼓流体动力学特性

薛晓宁，石 凯

（广东海洋大学机械与动力工程学院，湛江 524088）

为研究胶乳分离机转鼓离心流场动力学特性，基于FLUENT二相流模型，模拟了胶乳的分离过程以及转速、橡胶粒径对分离效果的影响，以浓乳的干胶含量为综合特征参数进行模型验证试验，理论分析影响分离速度的因素、碟片内液流的流动状态及轨迹、浓缩极限等问题。模型中设置鲜胶乳体积分数初始值为0.330，浓乳黏度0.038 48 mPa·s，表面张力系数0.034 N/m，橡胶粒径为5 μm，胶清按水的属性设置，碟片间隙为0.5 mm。计算结果表明：转鼓转速为

7 250 r/min时，胶乳进入转鼓10 s时橡胶粒子与胶清已呈现明显分离倾向；当转鼓分别为6 750、7 250和7 750 r/min时，浓乳中的干胶体积分数分别为0.588、0.613和0.636，转速越高，干胶体积分数越大，但转速超过7 250 r/min，干胶体积分数的增幅变缓，流体压力和结构应力也将明显增加；在7 250 r/min工作转速下，当胶乳粒径分别取1、2、3、4和5 μm时，浓乳中干胶的体积分数分别为0.354、0.392、0.447、0.531和0.601，浓乳中干胶体积分数随粒径增大而增加，轻相出口处因流体涡漩体积分数有一定波动。浓乳干胶含量的仿真结果与实测值高度接近，相对误差为3.83%，由此验证了模型的可靠性。轻/重相分离速度与粒径、转速直接相关，因科氏力轻相/重相轨迹与碟片母线有偏离，胶乳浓缩存在上限，轻/重相出料路径合理，离心去除细微杂质的能力强。研究结果为揭示胶乳离心浓缩机理、优化分离工艺及结构提供了理论参考。

胶乳；加工；模型；碟式分离机；高速转鼓；流体动力学；分离性能；数值模拟

0 引 言

中国天然橡胶种植加工主要分布在琼、粤、滇地区，鲜胶乳除加工成标准胶外，将其加工成浓乳（浓缩胶乳）是主要的利用方式，目前生产中均采用高速离心浓缩工艺，胶乳分离机是将鲜胶乳加工成浓乳和胶清的核心设备，高速转鼓是其关键功能部件。虽然碟式分离机的工程应用已非常普遍，但转鼓基本是引进仿制，在离心流场、结构及工作参数设计方面缺乏深入理论研究。转鼓高速旋转，结构封闭狭窄，目前难以直接测得转鼓的内流场物理参数。CFD分析是解决这一问题可行有效的技术手段。

近年，利用CFD研究流体机械内流场、结构及工作性能研究较多，在离心泵、水轮机、旋风分离器、水力旋流器等单相流、固液两相流范畴有较多的研究[1-12]；郑胜飞等[13-18]对卧螺离心机用多相流模型仿真模拟了内部流场，对其压力场、速度场、固/液相体积分数、影响流场及分离性能的参数（结构参数、物性参数和操作参数）进行了一定的研究，对管式离心机等也有研究报道。

碟式分离机转鼓结构决定其流场更为复杂。目前，已有的少量公开文献只涉及强度计算及结构设计，对内流场的研究较少。20世纪80年代出版的专著[19-20]对分离机结构、流场有一些解析理论描述并做了大的简化。相关的国外研究报道很少，国内文献基本属于常规参数设计及一般性应用问题探讨[21-27]。近年，赵志国等[25-27]对润滑油碟式分离机内部流场进行二维数值模拟，采用VOF多相流模型对分离过程、分离效率和油滴轨迹进行了模拟分析；转鼓中碟片数量众多，以往的分析基本按单层碟片间隙处理[19-20]，袁惠新等[28]采用三维数值模拟某型碟片分离机11层碟片内的液体速度、压力以及碟片之间流量及压力的变化，但文中未述及碟片内流体与原料进入、轻/重相排出、内腔流体状况之间的关系，这与实际有较大的差距。由于缺乏系统理论研究，在设计计算、性能评判、选型时往往只能凭借经验或试验。

天然橡胶物性独特，其流场的研究则更具特殊性，国内对胶乳分离机转鼓流体动力学的研究较少。薛晓宁等[29]利用CFD对生产用胶乳分离机的转鼓压力场、速度场以及出口速度场进行了定量分析与验证。干胶含量（dry rubber content）指在在鲜胶乳、浓乳或胶清中纯橡胶粒子的含量。本文通过CFD仿真及理论分析，对胶乳分离过程、分离性能及影响因素进行研究，利用浓乳的干胶含量作为特征参数验证计算模型，以期为揭示胶乳离心浓缩的机理、分离工艺及转鼓结构优化提供了理论依据。

1 转鼓与胶乳物性

分析对象为浙江轻机实业公司LX460胶乳分离机转鼓，转鼓内径为398 mm，碟片锥角为80°，为分析用模型的结构尺寸与实际机器一致，转鼓实物如图1所示。鲜胶乳经进料管从上端进入转鼓，再从碟片中性孔分配到各碟片间隙中完成分离；浓乳（轻相）向中心位置聚集，向上从轻相出口甩出；胶清（重相）向外移动，在内壁处汇集并向上移动，从重相出口调节螺丝甩出[30]。

图1 胶乳分离机转鼓Fig.1 Drum of latex separator

鲜胶乳来自橡胶树，是由水和胶乳粒子组成的多相体系生物合成产物，分散相包括橡胶粒子、非胶粒子，连续相则为胶清（水），纯橡胶粒子以液珠形式均匀分布于连续相胶清中。鲜胶乳中橡胶烃（干胶）成分25%～41.3%，水50%～70%，其余是非胶物质。鲜胶乳、浓乳、干胶和胶清的密度分别为0.96～0.98、0.92～0.96、0.91、1.02 g/cm3[31]。

2 内流场模型与仿真设置

2.1 流体动力学控制方程

离心分离的流体控制方程包括连续方程、动量方程、能量方程、组分方程、湍动能k方程和湍流耗散率ε方程，尽管这些方程中因变量各不相同，但它们均反映了单位体积内物理量的守恒性质。如果用φ表示通用变量，则上述各控制方程都可以表示成以下通用形式[32]：

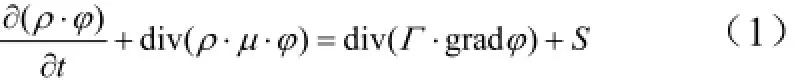
其展开形式为：

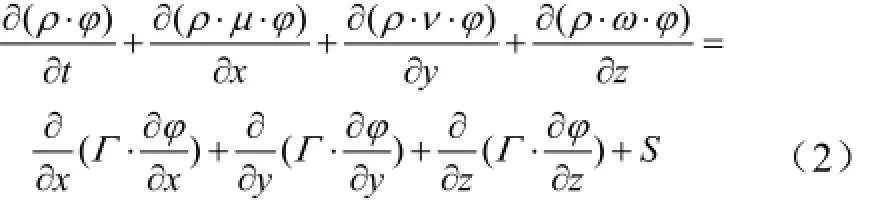
式中φ通用变量可以代表μ、υ、ω和T等求解变量，μ、υ、 ω分别为x、y和z方向的速度，m/s；T为时间，s；ρ为物料的密度， kg/m3；Γ广义扩散系数，S为广义源项。式（1）中∂(ρ·φ)/∂t为瞬态项，div(ρ·μ·φ)为对流项，div(Γ· gradφ) 为扩散项，S为源项。对于特定的方程，φ、Γ和S具有特定的形式，文献[32]详述了3个符号与各特定方程的对应关系。

离心分离机流体动力学由离心力场中的连续方程、欧拉平衡微分方程、柏努利方程、Navier Stokes微分方程组成，其特点在于采用柱坐标，详见文献[19]。本研究中未涉及能量交换等，故控制方程只涉及质量方程、动量方程，将Navier Stokes方程与液流的连续方程联立求解，就可描述离心力场中黏性液体的运动。

2.2 分析模型

关于分析模型的简化与假设、模型构建、网格划分、边界类型定义，薛晓宁等[29]在文献中有详述，在此不再赘述。取30张碟片创建的两相流二维分析模型如图2所示，模型划分为4个计算区域：1）分离区为碟片组及相邻碟片构成的锥形薄层区域，2）沉渣区为碟片大端以外与转鼓内壁之间的圆环区域，3）堰流区为流体入口到碟片组以及碟片组以上到出流区以下的部分，4）出流区为轻相、重相从转鼓排出的区域。

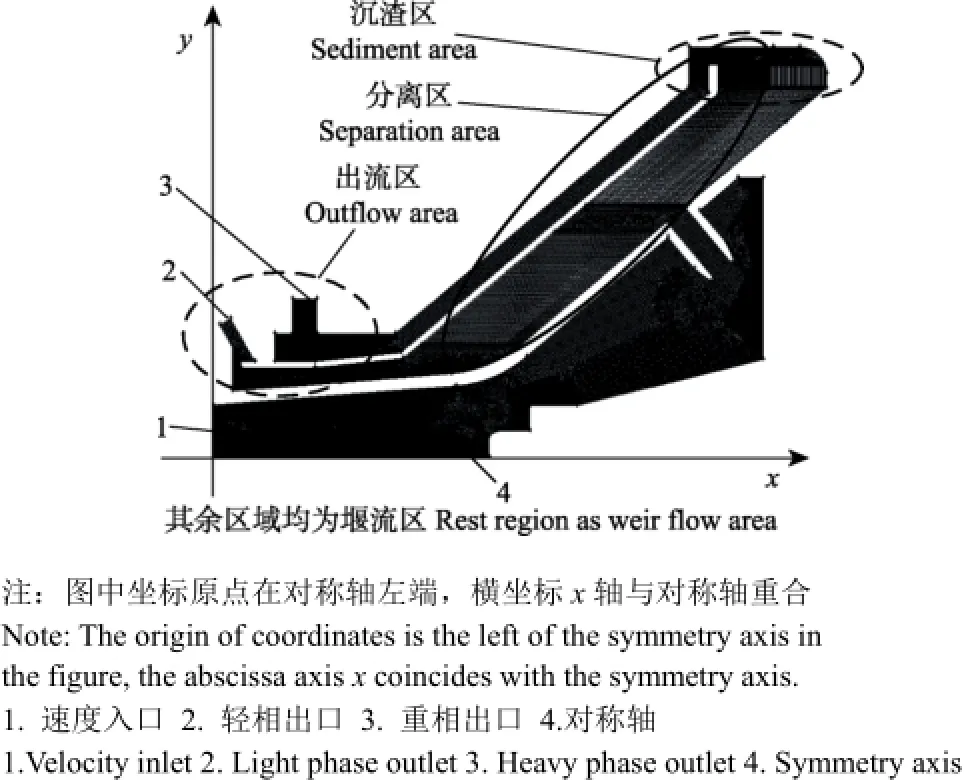
图2 转鼓流场二维模型Fig.2 Two-dimensional model of drum flow-field

2.3 多相流模型

选用压力基求解器，按动量方程、压力修正方程、能量方程、组分方程及其他标量方程的求解顺序，依次求解，可在分离求解和耦合求解之间实现转换，Time选择为瞬态Transient，2D Space选轴对称旋转Axisymmetric Swirl[32-33]。

多相流模型选用Mixture Model，该模型适用于各相速度不同、流动中有相混合或分离、离心沉降及相间曳力规律未知的多相流场合，另分散相橡胶粒子分布宽广，Mixture Model更合适[33]；为获得好的分离效果，转鼓内应尽量避免产生湍流，碟片间隙内为层流状态，故选择层流模型Viscous-Laminar[32]。

2.4 物料属性与参数设置

2.4.1 初始条件的确定

1）鲜胶乳的干胶体积分数：在鲜胶乳中橡胶粒子约占胶乳体积的20%～50%，橡胶烃（干胶）占25%～41%[31]，该值与胶树品系、树龄、开割时间等因素有关，因分析模型中是用干胶体积分数来表征橡胶含量。干胶体积分数乘以其密度再除以总物质密度即为总物质中的干胶质量分数。

2）胶乳粒子大小：橡胶粒子中的橡胶是非水溶性的，橡胶粒子一般是0.02～3 μm的球形粒子，但有些无性系成龄胶树所产胶乳中，粒子可能呈梨形甚至带着尾巴的，橡胶粒子的长度多数为2～4 μm，少数达到10 μm，但也是由球形粒子聚集而成[31]。本文胶乳粒子按球形处理，根据对不同粒径模型的计算调试结果，也考虑到高速下粒子的离心絮凝效应[20]作用，取粒子平均直径为5 μm。

3）进料速度：进料速度是由处理量计算得到，分析时分离机原料处理量为0.6 m3/h，则可计算出进料速度为0.252 m/s，初始速度设定为定值；进料速度不宜过大，太大可能会导致制成率下降，胶清中残留橡胶含量增加。

4）转鼓转速与碟片间隙：分离过程的仿真是按工作转速7 250 r/min分析，但分析转速对分离性能的影响时则取不同转速进行分析；碟片间隙为0.5 mm。

2.4.2 多相流设置

设置第一相为水（胶清），鉴于胶清中的橡胶及杂质含量极低，主要构成是水，故在软件材料库中选水的参数做为胶清的参数；设置第二相为浓乳，设定浓乳的密度为0.95 g/cm3、动力黏度为0.038 48 mPa·s，表面张力系数为0.034 N/m，橡乳粒子为球形[31]，选颗粒Granular，粒子平均粒径取5 μm。

边界条件的设置：相选择mixture，依据转鼓结构，设置重相、轻相出口的当量直径分别为12、6 mm，设定重相、轻相出口的出流比例分别为0.67、0.33；选择边界，设定内壁面为Moving Wall，设定旋转角速度为分析的值；选择胶清、浓乳的相，设定胶清、浓乳胶速度入口的速度均为0.252 m/s；选择Multiphase选项，根据粤西、海南开割前期鲜胶乳干胶含量的检测结果，定义鲜胶乳干胶体积分数为0.330。

2.5 求解算法与离散方法

压力速度耦合算法采用PISO算法，该法按预测-修正-修正求解，适于求解瞬态问题；梯度插值采用单元体最小二乘法插值（least squares cell based），对多面体网格求解更精确；离散方法（动量项）有5种格式，二阶离散格式更适合四边形网格的复杂流动。经过调试，本文选择二阶迎风格式；由于是高速旋转流场，故压力插值压力基分离求解器选择PRESTO！算法，求解控制方程采用SIMPLE方法[32-33]。

3 分离过程仿真与验证

3.1 仿真结果

初始化流场旋转速度7 250 r/min，设置时间步长为0.005 s、总迭代时间步数为10000。仿真结果如图3，反映了分离过程中不同时间点轻相-浓乳、重相-胶清中干胶体积分数的变化过程，描述了胶乳离心分离的动态过程。由图3可看出，转鼓达到工作转速时，浓乳与胶清在碟片分离区开始出现分离，胶清沿碟片向下运动，浓胶逐渐分离向中心聚集。图3各分图中右上方局部放大图，清晰地呈现了浓乳在碟片上端出口、胶清在斜通道末端的干胶体积分数变化情况。仿真结果表明：

1）鲜胶乳进入转鼓10 s时，橡胶粒子已在碟片上端出口有聚集，并开始向轻相出口移动，而胶清则向下运动，在转鼓体内壁处不断聚集，并沿重相通道向出口移动，两者已出现了明显的分离；在碟片小端出口干胶体积分数最大，随着分离时间的推移，浓乳、胶清分离程度愈加明显，轻相出口处的干胶体积分数逐渐增大，当超过120 s后，分离状态已趋于稳定状态，出口处浓乳、胶清的干胶体积分数均已稳定不变。

2）在7 250 r/min工作转速下，轻相出口浓乳干胶平均体积分数仿真结果为0.612 6，按总含固率62.5%的浓乳相对密度约为0.950 g/cm3进行计算[31]，对应的浓乳干胶质量分数0.582 2。

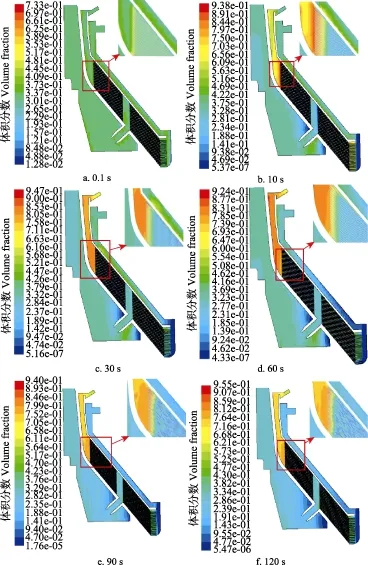
图3 分离过程中不同时间点浓乳和胶清中干胶体积分数图Fig.3 Dry rubber volume fraction diagrams of concentrated latex and skim serum at different simulation time point of latex separation process

3.2 仿真结果的验证

3.2.1 验证方法

由于目前测试技术及仪器直接测取内流场参数及微观分离过程实现难度极大，本文以浓乳干胶含量做为特征参数来验证模型的正确性。浓乳中的干胶含量是综合反映转鼓结构、胶乳特性、分离转速等的特征参数，并且干胶含量检测易行可靠。

试验材料：采自三叶胶树的当天含氨新鲜胶乳，鲜胶乳质量良好（挥发脂肪酸值低于0.06），无异味、凝粒。根据干胶含量测定标准GB/T8299-2008，采用化学凝固标准方法在加工厂化验室完成。将鲜乳胶或浓缩胶乳试验原料稀释至总含固率为20%，并用乙酸酸化，然后将凝固的橡胶压成薄片，在70 ℃温度下干燥，依据测定数据可计算得到干胶含量。

仪器：分析天平（中衡精密仪器有限公司）、101A-2型数显电热鼓风干燥箱（上海浦东荣丰科学仪器公司），专用压片用具，玻璃皿或瓷皿，滤纸。试剂：乙酸，20 g/L的水溶液。

试验用离心设备采用浙江轻机制造的LX-460胶乳分离机（结构参数与分析模型一致），机器状态良好，为保证试验条件与建模参数接近，进料口采用孔径11.5 mm大进料管，重相胶清出口采用孔长9.5 mm调节螺丝，转鼓实际工作转速7 213 r/min，进料10 min后从浓乳出口采样。

3.2.2 验证结果

仿真模型的设定：生产中该型分离机处理胶乳的生产率按576 kg/h，鲜胶乳干胶体积分数为0.33，按其密度0.965 g/cm3计算得鲜胶乳干胶质量分数为0.31845，转速为7 250 r/min。仿真结果：浓乳干胶体积分数为0.612 6，按浓乳密度取0.95 g/cm3计算，得浓乳的干胶质量分数仿真值为0.582 2。

试验于2016年7月在广垦橡胶湛江分公司开展，测得试验用鲜胶乳的干胶质量分数为0.3582，受2015年10月台风重创，胶树开割时间退迟，试验时刚开割，故干胶含量偏高，一般开割一段时间后鲜胶乳的干胶质量分数降到0.25～0.27范围。为保证试验用鲜胶乳干胶体积分数与分析模型一致，对原料鲜胶乳通过计算加水稀释，并测得稀释后的鲜胶乳干胶质量分数为0.3111，与分析模型的设定值0.31845接近。离心浓缩后，浓乳干胶质量分数测定结果为0.6054。

试验条件与仿真设定条件高度吻合，仿真值与实测值接近，相对误差为3.83%，由此验证了模型的可靠性。

3.3 仿真分析讨论

3.3.1 转速对浓乳体积分数的影响

图4为时间点120 s时出流区的浓乳干胶体积分数，提取轻相出口处从A到B路径的浓乳干胶体积分数值，则可得相应转速下轻相出口的浓乳干胶体积分数变化曲线如图5所示，转速分别为6 750 、7 250 和7 750 r/min时，浓乳干胶平均体积分数分别为0.587 5、0.612 6和0.635 8。由此可知，在确定的转鼓结构和相同的分离时间下，转速越高，浓乳干胶的体积分数越大，即浓乳中干胶含量越高。

浙江轻机实业有限公司造胶乳分离机与广重胶乳分离机的转鼓核心结构参数相同。早期浙江轻机转鼓转速比广重转鼓约低230 r/min，使用中存在浓乳干胶含量指标不稳定、制成率偏低的不足，而结构及参数相同的广重转鼓则无同样类似问题，九十年代末浙江轻机公司将转速提高至与广重转鼓接近，原来的问题不再出现，由此实证了转速影响分离效果的仿真结果的正确性。

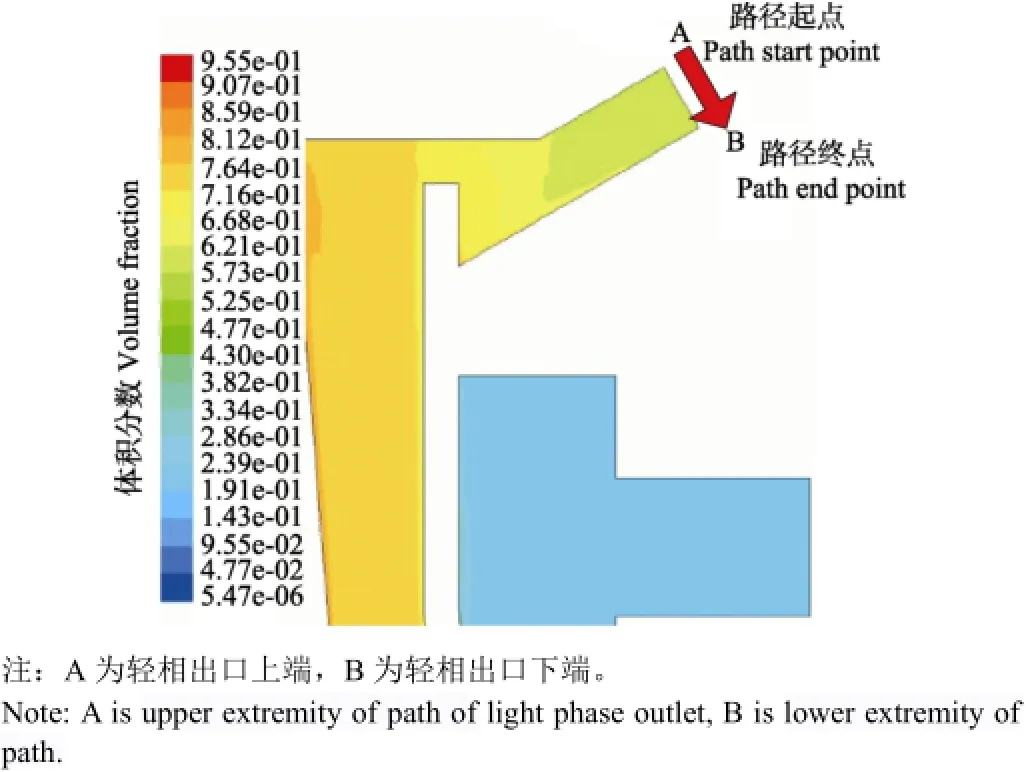
图4 仿真时间点120 s时出流区干胶体积分数Fig.4 Dry rubber volume fraction of the outflow area when simulation time point is 120 s

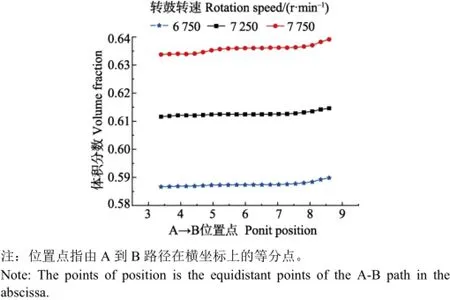
图5 A-B路径轻相出口浓乳干胶体积分数变化曲线Fig.5 Dry rubber volume fraction curve of concentrated latex along A-B path in light phase outlet

3.3.2 影响分离转速的因素

表1是转鼓体在不同转速下受到的最大离心流体压力、结构应力的模拟结果，转速增加，可将胶清中更小的胶乳分离出来，但同时流体压力、结构应力也会大幅增加，这将对转鼓的结构、材料及制造工艺提出更严苛的要求。分析图5可知，随着转速增加体积分数值将相应提高，但转速超过7 250 r/min后，浓乳干胶体积分数的增幅趋缓。所以，确定转鼓转速参数时，需要在转鼓的分离性能、强度及安全性、制造成本之间综合平衡。目前工作转速下，胶清中的极微小橡胶粒子无法分离出来，约有4%～6%的橡胶随胶清排放。

3.3.3 橡胶粒径对浓乳干胶体积分数的影响

粒径分别设置为1、2、3、4和5 μm时，两相流模型的仿真结果如图6所示，在工作转速下轻相出口浓乳的体积分数仿真结果分别为0.354、0.392、0.447、0.531和0.601。

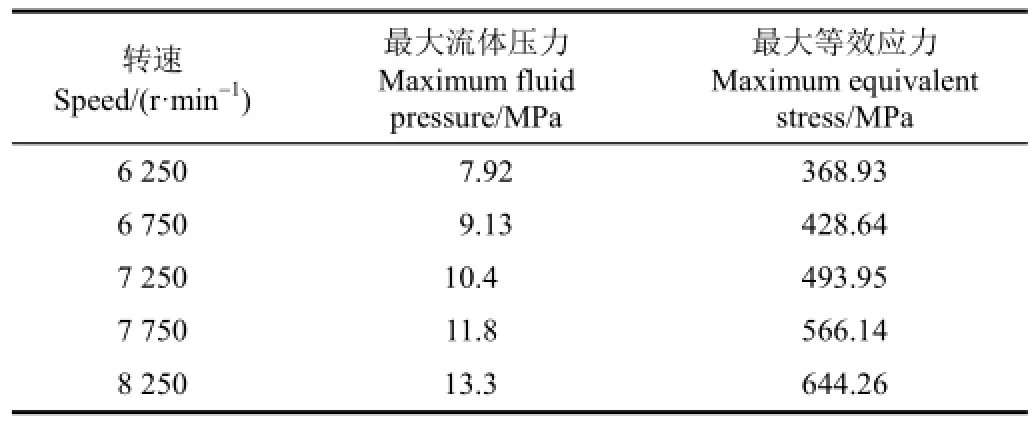
表1 不同转速下最大流体压力和转鼓体最大等效应力Table1 Maximum fluid pressure and maximum equivalent stress of drum body at different speed

橡胶粒子的大小不同时，所受离心力也不同，粒径较大时其密度相对要小一些，所受的离心力也略微要小一点，因此，大橡胶粒子更易与胶清分离。这种情况的典型例证是牛奶分离机在分离奶油时需将牛奶加热到35 ℃，加热的目的就是为了增大乳脂的脂肪球，获得更佳分离效果[34]。据文献[31]胶清中残留的橡胶粒子直径小于0.15 μm，说明离心分离实际上已把一些很小（0.15～1 μm）的粒子从胶清中分离出来了，可能原因：1）微小橡胶粒子在离心絮凝效应[20]作用下会聚集增大，2）胶乳属于活体，其物理化学特性、微生物可能导致粒子变大。

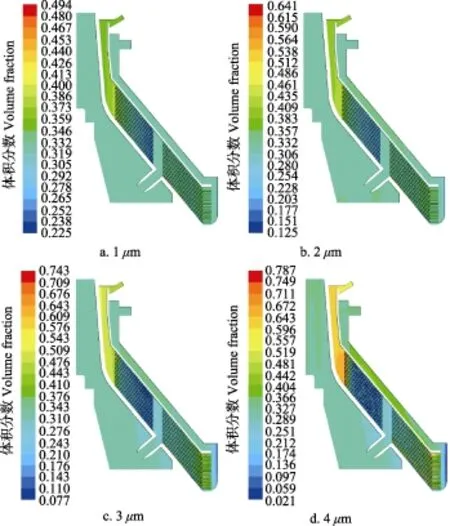
图6 鲜胶乳中不同橡胶粒径时的干胶体积分数图Fig.6 Dry rubber volume fraction diagrams of different rubber particle size of raw latex

3.3.4 轻相出口体积分数的波动

由图3、图4可知：仿真时间点30～120 s，轻相出口处浓乳干胶体积分数均存在一定的下降。造成该现象的可能原因，速度场仿真分析[29]表明，此处存在较大流体速度涡漩；另外，顶碟上端与转鼓盖之间有一环状缝隙，浓乳从缝隙进到出口孔之前，浓乳受到强大离心力从出口甩出，这将导致浓乳干胶体积分数有一定的下降。为降低涡漩，有必要优化轻、重相出口结构。

4 流体动力学特性理论分析

4.1 轻相与重相的分离速度

设胶清的动力黏度η，mPa·s；胶清、橡胶粒子的密度分别为γ、γ2，kg/m³；粒子半径r，mm；回转半径R，mm。在重力场中，由于橡胶粒子和胶清有密度差，橡胶粒子会上浮而胶清则会下沉。橡胶粒子上浮时，受到重力、上浮力和摩擦阻力，受力平衡时粒子匀速上浮，橡胶粒子与胶清之间存在分离速度，但在重力场中分离速度极其缓慢，24 h内上升不到1 mm[34]，无实际工程应用意义。

设转鼓转速为n，r/min；分离因数Fr=a/g，离心加速度a，m/s²；重力加速度g，m/s²；Fr反映离心分离的强度，欲取得良好的分离效果，Fr必须达到一定的值。经计算得到，在碟片中性孔处，橡胶粒子受到的离心加速度相当于g的7 051倍。

高速离心分离时分离速度将大幅增加，在碟片中粒子的分离速度[15]为：

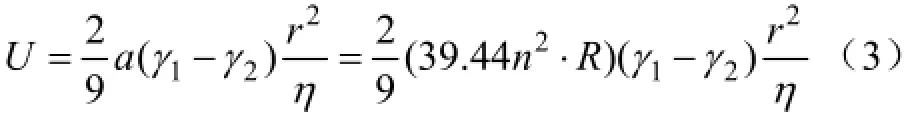
将胶乳物性及转鼓参数带入式（3）得到的规律曲线（从略）可知：橡胶粒子越大，胶清黏度越小，胶清与粒子的密度差越大，转速越高、回转半径越大时，分离速度越大，就越容易获得高的干胶含量和制成率。粒子所受离心力随回转半径增加而加大，胶清往碟片周边运动过程中，其中夹带的橡胶粒子将按大小顺序不断从胶清中逐渐被分离出来。

4.2 碟片间隙内胶乳的流动及运动

通过解Navier-Stokes方程可得到描述碟片间隙内液流及沉降过程规律的无量纲特性准数λ值，λ值计算式见文献[19-20]。λ值是判定层流转变为湍流的指标，当λ=2π时碟片中的层流转变为湍流，碟式分离机λ值推荐取5～12[20]。在胶乳分离机上代入有关参数计算得λ=5，故可判断碟片间浓乳、胶清的流动为层流。

在碟片间隙内胶清、杂质将向外移动，而橡胶则向中心移动，液流的运动状态决定于液体质点各方向分速度，液流运动由沿碟片母线方向的径向速度、科氏力引起的相对周向速度构成。液流沿碟片母线方向的运动，离碟片表面愈远，液流间的内摩擦力愈小，则相对移动的距离就愈大，径向速度变大。同时，因科氏力的作用，液流质点绝对周向速度有所降低，周向速度略滞后于碟片表面，这将使质点离心力减小，最终导致液流径向速度减小，且离碟片愈远，滞后程度越大，因此碟片附近的液流相对滞后比较小，受到的离心力大，其沿母线的运动必然快于液流中间层。周向速度的减小量在数值上远远小于旋转速度。

由上述分析，在碟片间隙内浓乳、胶清的运动轨迹可依照图7来描述[34]，图中实线、虚线分别代表重相胶清、轻相橡胶粒子的运动轨迹，轨迹与碟片母线有偏离、不平行，准数λ值越大，偏离程度将加大。

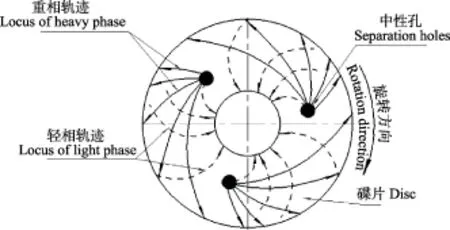
图7 碟片间隙内轻相/重相的运动轨迹Fig.7 Movement locus of light/heavy phase in disc clearance

4.3 胶乳浓缩极限

仿真结果表明，随着分离转速的增加，轻相出口浓乳平均体积分数也将逐步增大，此时浓乳的黏度也将伴随干胶含量的增加而加大，粒子运动阻力增大，同时浓乳沿碟片往中心运动，使回转半径减小，在此过程中橡胶粒子的离心力逐渐减小，进一步被浓缩的趋势逐渐变弱。这揭示了离心浓缩天然胶乳最终的干胶含量存在上限的机制，按文献[31]试验得到的浓乳最大干胶质量分数不超过0.67，这可以通过采用进料孔径最小的进料管与出料孔长度最大的调节螺丝来实现[31]。从设备操作角度，也不宜过度浓缩，否则会导致碟片间隙等通道内产生凝胶，导致通道堵塞、分离性能恶化。

4.4 轻/重相路径与杂质的分离

当胶乳浓缩达到预期的程度后，应尽快从转鼓中排出，浓乳应经历尽可能短的路径，即从转鼓排出；胶清的排出路径应适当曲折迂回，以增加胶清在转鼓中停留的时间，以及在大回转半径处分离出更小的橡胶粒子的概率。另外，因胶清出口靠近中心，流出时受到的离心力小，这有利于使杂质沉积在转鼓内壁，提高胶清清洁度。转鼓结构满足上述要求。

从胶乳中可分离出的杂质极限粒子直径d计算式[20]：

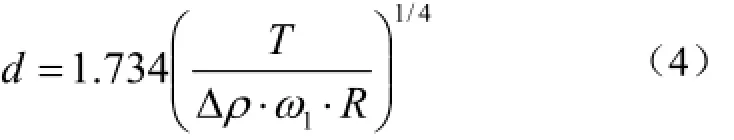
式中T为胶乳的温度 ，K，取300 K；Δρ为杂质与胶乳的密度差，g/cm3；ω1为转鼓角速度，rad/s；R为杂质在转鼓中的回转半径，mm。

如取胶泥杂质密度为2.7 g/cm3，经计算得中性孔处可分离出的杂质极限粒径为0.05 μm，故具有强大的除杂能力。杂质的存在会增加碟片间隙内紊流的可能性[20]，也会缩短清洗转鼓的间隔时间，对此，建议改进胶乳加工工艺，在进行离心浓缩之前，先将鲜胶乳采用专用碟片分离机除去绝大部分杂质。

5 结 论

1）构建的两相流模型清晰地呈现了胶乳的动态分离过程，胶乳进入转鼓历经120 s时浓乳、胶清的干胶体积分数均已稳定不变，浓乳中干胶体积分数达到最大值；在7 250 r/min工作转速下仿真结果对应的干胶质量分数计算值为0.582 2，仿真结果与浓乳干胶含量实测值接近，与实测值的相对误差为3.83%，分析模型具可靠性。

2）当转速为6 750 、7 250 和7 750 r/min时，浓乳干胶体积分数分别为0.587 5、0.612 6和0.635 8，当粒径分别取1、2、3、4和5 μm时，工作转速下浓乳的干胶体积分数分别为0.354、0.392、0.447、0.531和0.601，计算结果表明，转速、粒径显著影响天然橡胶分离速度，转速越高，浓乳中干胶含量增加，胶清残留橡胶减少，大橡胶粒子更易分离，但随转速增加，流体压力和结构应力也将明显增加。

3）碟片内胶乳的流动为层流，橡胶粒子、胶清的运动轨迹是径向和周向运动的合成，橡胶粒子、胶清的运动轨迹与母线有偏离，偏离程度与特性准数值有关，揭示了胶乳浓缩存在上限值的根本原因，浓乳/胶清历经路径设计有利于防止凝胶产生和充分除杂，转鼓具备离心去除极限粒径为0.05 μm细微杂质的性能，建议从工艺上将除杂安排在离心浓缩之前。

研究方法和结果为揭示胶乳分离机离心浓缩机理、优化分离工艺参数和转鼓结构提供了理论参考，为进一步研究打下了基础，今后，在橡胶-胶清-杂质三相流三维离心流场下结构、物性、操作参数对流体动力学特性的影响等方面，有待做进一步深入的研究。

[1] 王福军，流体机械旋转湍流计算模型研究进展[J]. 农业机械学报，2016，47(2)：1－14.

Wang Fujun. Research progress of computational model for rotating turbulent flow in fluid machinery[J]. Transactions of the Chinese Society of Agricultural Machinery, 2016, 47(2): 1－14. (in Chinese with English abstract)

[2] 裴吉，王文杰，袁寿其，等. 低比转数离心泵内部非定常流动特性数值预测[J]. 农业机械学报，2014，45(1)：79－83，88.

Pei Ji, Wang Wenjie, Yuan Shouqi, et al. Numerical prediction of inner flow unsteadiness in a low-specific speed centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(1): 79－83, 88. (in Chinese with English abstract)

[3] 邵春雷，顾伯勤，陈 晔. 离心泵内部非定常压力场的数值研究[J]. 农业工程学报，2009,25（1）：75-80

Shao Chunlei, Gu Boqin, Chen Ye. Numerical simulation of unsteady pressure field in centrifugal pumps[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(1): 75－80. (in Chinese with English abstract)

[4] 辛喆，吴俊宏，常近时. 混流式水轮机的三维湍流流场分析与性能预测[J]. 农业工程学报，2010，26(3)：118－124.

Xin Zhe, Wu Junhong, Chang Jinshi. Flow field analysis and performance prediction of three-dimensional turbulent flow in Francis turbine[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2010, 26(3): 118－124. (in Chinese with English abstract)

[5] 夏得峰，林光荣，王明贤，等. 基于计算流体力学的旋风除尘器优化[J]. 中国粉体技术，2015，21(1)：100－102.

Xia Defeng, Lin Guangrong, Wang Mingxian, et al. Cyclone optimization based on computational fluid dynamics[J]. China Power Science and Technology, 2015, 21(1): 100－102. (in Chinese with English abstract)

[6] 王江云，毛羽，王娟. 立式天然气多管旋风分离器内流体的流动特性[J]. 化工机械，2015，42(2)：225－229.

Wang Jiangyun, Mao Yu, Wang Juan. Flow characteristic of vertical multi-tube cyclone separation for natural gas[J]. Chemical Machinery, 2015, 42(2): 225－229. (in Chinese with English abstract)

[7] 蒋梦婷，王博，陈言信，等．旋风分离器内高速旋转流场的数值计算方法选择[J]．环境工程学报，2012，6(8)：2736－2743．

Jiang Mengting，Wang Bo, Chen Yanxin, et al. Selection of numerical approaches to calculate the high-speed rotating flow field within a cyclone separator. Chinese Journal of Environmental Engineering, 2012, 6(8): 2736－2743. (in Chinese with English abstract)

[8] 崔瑞，王光辉，李茂林.双锥旋流分离器内固-液分离过程的数值模拟[J]. 中国粉体技术，2015，21(3)：6－11.

Cui Rui, Wang Guanghui, Li Maolin. Numerical simulation of solid-Liquid separation process in dual-cone hydrocyclone[J]. China Power Science and Technology, 2015, 21(3): 6－11. (in Chinese with English abstract)

[9] 舒朝晖，杨拓，周宇，等. 除油旋流器操作参数对分离效率影响的数值模拟[J]. 石油化工设备，2015，44(5)：1－6.

Shu Chaohui, Yang Tuo, Zhou Yu, et al. Numerical simulation of the effect of operational on separation efficiency in de-oliing hydrocyclones[J]. Petro-Chemical Equipment, 2015, 44(5): 1－6. (in Chinese with English abstract)

[10] 崔岩，王建军，孙茂生，等. 水力旋流除砂器内液-固两相流动试验与数值模拟[J]. 石油机械，2015，43(11)：123-128.

Cui Yan, Wang Jianjun, Sun Maosheng, et al. Expeiment and numerical simulation on the liquid-solid flow in hydrocyclone desander[J]. China Petroleum Machinery, 2015, 43(11): 123－128. (in Chinese with English abstract)

[11] 刘书孟，董喜贵，刘鼎恒，等. 黏度对三相分离旋流器性能影响的数值模拟[J]. 石油化工设备，2014，43(3)：27－30.

Liu Shumeng, Dong Xigui, Liu Dingheng, et al. Numerical simulation of influence of viscosity on the separation performance of three-phase hydrocyclones[J]. Petro-Chemical Equipment, 2014, 43(3): 27－30. (in Chinese with English abstract)

[12] 喻黎明，邹小艳，谭弘严，等. 基于CFD-DEM耦合的水力旋流器水沙运动三维数值模拟[J]. 农业机械学报，2016，47(1)：126－13.

Yu Liming, Zou Xiaoyan, Tan Hongyan, et al. 3D numerical simulation of water and sediment flow in hydrocyclone based on coupled CFD-DEM[J]. Journal of Agricultural Machinery, 2016, 47(1): 126－13. (in Chinese with English abstract)

[13] 郑胜飞，任欣，谢林君. 卧螺离心机流场的三维数值模拟[J]. 轻工机械，2009，27(6)：26－29.

Zhen Shengfei, Ren xin, Xie Linjun. Three-dimensional numerical simulation of spiral centrifuge flow field[J]. Light Industry Machinery, 2009, 27(6): 26－29. (in Chinese with English abstract)

[14] 于萍，林苇，王晓彬，等. 卧螺离心机离心分离场速度仿真分析[J]. 机械工程学报，2011，47(24)：151－157.

Yu Ping，Lin Wei，Wang Xiaobin，et al. Velocity simulation analysis on centrifugal separation field of horizontal spiral centrifuge[J]. Journal of Mechanical Engineering, 2011, 47(24): 151－157. (in Chinese with English abstract)

[15] Zhu Guorui, Tan Wei. Experimental and numerical study of the concentration distribution in a horizontal screw decanter centrifuge[J]. Ind Eng Chem Res, 2013, 52: 17249－17256.

[16] 付双成，董连东，袁惠新. 基于Euler多相流模型的卧螺离心机速度场数值模拟与分析[J]. 化工进展，2014，33(1)：36－42.

Fu Shuangcheng, Dong Liandong, Yuan Huixin. Numerical simulation and analysis on flow field in a decanter centrifuge based on the Euler model[J]. Chemical Industry and Engineering Progress, 2014, 33(1): 36－42. (in Chinese with English abstract)

[17] 周翠红，凌鹰，申文君，等. 卧式螺旋沉降离心机污泥脱水模拟研究[J]. 机械工程学报，2014，50(16)：206－212.

Zhou Cuihong, Ling Ying, Sheng Wenjun, et al. Numerical study on sludge dewatering by horizontal decanter centrifuge[J]. Journal of Mechanical Engineering, 2014, 50(16): 206－212. (in Chinese with English abstract)

[18] 朱明军，袁惠新，付双成. 卧螺式浮渣分离离心机两相数值模拟[J]. 化工进展，2015，34(2)：336－342，375

Zhu Mingjun, Yuan Huixin, Fu Shuangcheng. Two-phase numerical simulation research in a decanter centrifuge of separating floating sludge[J]. Chemical Industry and Engineering Progress, 2015, 34(2): 336－342, 375. (in Chinese with English abstract)

[19] 索科罗夫著，汪泰临，孙启才，陈文梅译. 离心分离理论及设备[M]. 北京：机械工业出版社，1986.

[20] 孙启才，金鼎五. 离心机原理结构与设计计算[M]. 北京：机械工业出版社，1987.

[21] 杨如惠. 碟式离心机的分离影响因素及模型浅析[J]. 合成技术及应用，2010，25(3)：56－58.

Yang Ruhui. The analysis of classification influence factor and simulation about disc centrifuge[J]. Synthetic Technology and Application, 2010, 25(3): 56－58. (in Chinese with English abstract)

[22] 袁惠新，王飞，付双成，等. 碟式离心机分离性能的研究[J]. 化工机械，2011，38(2)：157－159

Yuan Huixin, Wang Fei, Fu Shuangcheng, et al. Research on separation performance of disc centrifuge[J]. Chemical Machinery, 2011, 38(2): 157－159. (in Chinese with English abstract)

[23] 濮伟. 碟式分离机重液出口影响因素及参数关系图[J]. 过滤与分离，2006，16(3)：29－30，33.

Pu Wei. Influence factors and parameter-relation diagram of the exit of heavy liquid in disc separator[J]. Journal of Filtration & Separation, 2006, 16(3): 29－30，33. (in Chinese with English abstract)

[24] 刘广明. 碟式分离机分离效果的分析研究[J]. 过滤与分离，2009，19(1)：27－30 Liu Guangming. Analysis and research for the separation effect of disc separator[J]. Journal of Filtration & Separation, 2009, 19(1): 27－30. (in Chinese with English abstract)

[25] 赵志国，石博强，李宴. 润滑油分离机内部流场数值模拟与分离效率分析[J]. 农业工程学报，2011，27(8)：163－168.

Zhao Zhiguo, Shi Boqiang, Li Yan. Separation efficiency analysis and numerical simulation of lubricant separator inner flow field pump[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2011, 27(8): 163－168. (in Chinese with English abstract)

[26] 赵志国，石博强，李宴，等. 基于Fluent的碟式分离机杂质颗粒运动流场分析[J]. 煤矿机械，2011，32(3)：112－114.

Zhao Zhiguo, Shi Boqiang, Li Yan, et al. Analysis of movement flow of centrifuge granule based on fluent [J]. Coal Mine Machinery, 2011, 32(3): 112－114. (in Chinesewith English abstract)

[27] Zhao Zhiguo. The influence of structural changes on the interior flow field’s characteristics of disc separator[J]. Procedia Engineering, 2011(15): 5051－5055.

[28] 袁惠新，侯新瑞，付双成. 碟片式离心机内流动的数值模拟[J]. 化工进展，2014，33(6)：1403－1407

Yuan Huixin, Hou Xinrui，Fu Shuangcheng. Numerical simulation of the flow in a disc centrifuge[J]. Chemical Industry and Engineering Progress, 2014, 33(6): 1403－1407. (in Chinese with English abstract)

[29] 薛晓宁，石凯. 胶乳分离机高速转鼓内流场的数值分析[J].流体机械，2016，44(8)：22－27.

Xue Xiaoning, Shi Kai. Numerical analysis on flow-field characteristics of high-speed bowl of latex disc-separator[J]. Fluid Machinery, 2016, 44(8): 22－27. (in Chinese with English abstract)

[30] 薛晓宁. 平带传动碟式分离机[P]. 中国：ZL2008100290738，2011-04-13.

[31] 何映平. 天然橡胶加工学[M]. 海口：海南出版社，2007：9－128.

[32] 王福军. 计算流体动力学分析-CFD软件原理与应用[M].北京：清华大学出版社，2004：7－13

[33] 李进良，李承曦，胡仁喜. 精通FLUENT6.3流场分析[M].北京：化学工业出版社，2009：10－189

[34] 武建新. 乳品技术装备[M]. 北京：中国轻工业出版社，2000：36－39

Fluid dynamics characteristic of high-speed drum for latex separator

Xue Xiaoning, Shi Kai
(College of Mechanical and Power Engineering, Guangdong Ocean University, Zhanjiang, 524088, China)

Latex separator is the key part of latex concentrated processing equipment, and belongs to disc separator. Disc separator is widely used in various industrial sectors. At present, the theory research on flow field and structure of separator drum is still not perfect, which results in the lack of theoretical guidance for the optimization of flow field and structure about the drum. To solve this problem and to reveal the latex fluid dynamics characteristics of the drum, the research on the flow field of latex drum was carried out. A mathematical model for the flow field of centrifugal separation was established. Based on FLUENT and two-phase flow model built, the fluid dynamics characteristics were explored through simulation and theoretical analysis. In the simulation of latex separation process, the separation effects under different speeds and different rubber particle sizes were conducted. The test of model validation was carried out in the branch factory affiliated to Guangdong Agricultural Reclamation Rubber Group in Zhanjiang in July 2016. The testing separator was the LX-460 type latex separator whose drum parameters were the basis of the construction of analysis model. The measured dry rubber content as comprehensive characteristic parameter was used to validate the model. Based on the mechanics theory, the factors affecting the separation speed of light and heavy phases, the flow state and fluid flow trajectory within the disc gap, the concentration limit and other aspects were analyzed and discussed. For the parameter setting of the model, the kinematic viscosity of concentrated latex was 0.03848 mPa·s, the surface tension coefficient was 0.034 N/m, the rubber particle size was 5 μm, the dry rubber volume fraction of raw latex was 0.33, the latex temperature was 26℃, the disc clearance was 0.5 mm, and the properties of latex skim were set as that of water in material library. The research results showed that: At 7 250 r/min rotation speed of the drum, the dynamic process of latex separation was clearly displayed. The rubber particles showed a tendency of separating from latex skim 10 seconds after fresh latex entered the drum. The dry rubber volume fraction of concentrated latex at light phase outlet completely reached the maximum stable value 120 seconds after latex entered the drum. When the rotational speed was respectively 6 750, 7 250 and 7 750 r/min, the simulated dry rubber volume fraction of concentrated latex was 0.587 5, 0.612 6, 0.635 8 respectively at light phase outlet. The higher the speed, the larger the volume fraction of concentrated latex. But when the speed exceeded 7 250 r/min, the increase in the volume fraction of dry latex grew slow, and the fluid pressure and structural stress would increase obviously. When the latex particle sizes were respectively 1, 2, 3, 4 and 5 μm, the simulated values of dry rubber volume fraction at light phase outlet were 0.354, 0.392, 0.447, 0.531 and 0.609 at the 7 250 r/min speed. The dry rubber volume fraction of concentrated latex increased with the increase of the particle size. The dry rubber volume fraction at light phase outlet had a little fluctuation caused by a vortex. The simulation result was in agreement with the experimental result of concentrated latex. The relative error was 3.83%. The reliability of the analytical model was verified. In addition, the theoretical analysis results showed that the factors that significantly affected the separation speed between light and heavy phases were particle size, rotating speed and turning radius of particles. The trajectory of light and heavy phases between the discs would deviate from the conical disc busbar because of the the Coriolis force effect. With the increase of dry rubber content in the process of centrifugal concentration, the viscosity and the particle resistance increased gradually, the turning radius decreased gradually, and there existed the upper bound for latex concentration. The drum structure would be a reasonable design with shorter light-phase discharging path and longer heavy-phase discharging path. The minimum particle size of 0.05 μm would be obtained from the neutral hole by theoretical calculation. The centrifugal removal of tiny impurities was superior. The results provide more theoretical guidance and reference for revealing the mechanism of latex centrifugal concentration, and optimizing separation process and drum structure.

latexes; processing; models; disc separator; high-speed drum; fluid dynamics; separation performance; numerical simulation

10.11975/j.issn.1002-6819.2017.05.040

TH123; TQ332.1

A

1002-6819(2017)-05-0279-08

薛晓宁，石 凯. 胶乳分离机高速转鼓流体动力学特性[J]. 农业工程学报，2017，33(5)：279－286.

10.11975/j.issn. 1002-6819.2017.05.040 http://www.tcsae.org

Xue Xiaoning, Shi Kai. Fluid dynamics characteristic of high-speed drum for latex separator[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(5): 279－286. (in Chinese with English abstract)

doi：10.11975/j.issn.1002-6819.2017.05.040 http://www.tcsae.org

2016-05-11

2016-12-20

广东省科技计划（2009B020312003），广东省教育厅科研基金项目（B9810），海南省企业新型胶乳分离机研制合作项目（QH2005-02）。

薛晓宁，男（汉），青海西宁人，副教授，主要从事碟式分离机设计及理论、农牧渔业技术装备的研究。湛江，广东海洋大学，524088。Email：gdouxue@126.com