基于称重式蒸渗仪实测日值评价16种参考作物蒸散量(ET0)模型**
刘晓英,李玉中,钟秀丽,曹金峰,袁小环
(1.中国农业科学院农业环境与可持续发展研究所/农业部旱作节水农业重点实验室,北京 100081;2.北京草业与环境研究发展中心,北京 100097)
基于称重式蒸渗仪实测日值评价16种参考作物蒸散量(ET0)模型**
刘晓英1,李玉中1,钟秀丽1,曹金峰1,袁小环2
(1.中国农业科学院农业环境与可持续发展研究所/农业部旱作节水农业重点实验室,北京 100081;2.北京草业与环境研究发展中心,北京 100097)
参考作物蒸散量(ET0)的准确估算是作物需水量及区域农业水分供需计算的关键,尽管已提出大量方法,但缺乏基于实测值的严格检验。本文利用北京小汤山2012年称重式蒸渗仪实测日值,检验16个ET0模型,包括5个综合法、6个辐射法、5个温度法模型。依据均方根误差RMSE值,各模型估算效果的排序为FAO79 Penman=1963 Peman>1996 Kimberly Penman>FAO24 Penman>FAO56 Penman-Monteith(PM)>Turc>FAO24 Blaney-Criddle(BC)>DeBruin-Keijman>Jensen-Haise>Priestley-Taylor (PT)>FAO24 Radiation>Hargreaves>Makkink>Hamon>Mcloud>Blaney-Criddle (BC)。总体而言,综合法表现最好,其RMSE在1.33~1.47mm∙d-1,以FAO79 Penman和1963 Penman为最好;辐射法次之,其RMSE在1.48~1.77mm∙d-1,以Turc最好;温度法检验效果最差,其RMSE在1.50~2.68mm∙d-1,以FAO24 BC为最好。FAO79 Penman和1963 Penman比最好的辐射法和温度法模型的精度分别高10%和13%。综合法、辐射法模型普适性好于温度法的原因在于其均含有影响ET0的关键因子——辐射或饱和水汽压差VPD。所有模型均具有低蒸发条件下高估、高蒸发条件下低估的阈值特点,综合法及辐射法平均低估0.14mm∙d-1和0.33mm∙d-1,而温度法平均高估0.52mm∙d-1。前两类方法ET0阈值相对较低,更适于低蒸发力条件,而温度法较适于高蒸发力条件。所有综合法、辐射法模型及温度法的Hargreaves和FAO24 BC法估算值与实测值变化趋势一致,说明模型结构合理,可通过参数校正提高精度;但对于与实测值趋势不吻合的温度法,模型结构尚需优化。VPD和最大湿度RHx是影响综合法、辐射法估算偏差的两大主要因子,其中VPD对低估类模型偏差影响最大,且偏差随着VPD增加而增大;而RHx对高估类综合法模型(1963 Penman、FAO79 Penman)偏差影响最大,且偏差随RHx增加而减小。校正后的PT (1.38)、Makkink(0.83)、Turc(0.014)及Hamon(1.248)系数大于原系数,而Hargreaves(0.0019)和BC(0.192)校正系数低于原系数。此外,PT与Hamon的系数利用最小相对湿度、Turc和Makkink系数利用VPD、Hargreaves和BC系数利用辐射或日照时数能得到最佳估算。FAO56 PM表现不佳(RMSE=1.47mm∙d-1)的原因与站点气候干燥程度、较低的空气动力项权重有关。后人对原始 Penman式的诸多修正并没有显著改善精度,因此建议在类似气候条件地区继续使用老版本 Penman式。同时,对FAO56 PM的进一步检验将有助于回答“FAO56 PM是否真正比其它综合法具有优势,在何种气候下表现好,在高蒸发条件下低估是否为普遍现象”等科学问题。
Penman-Monteith; Priestley-Taylor; Turc; Hargreaves; Makkink; Blaney-Criddle; FAO24 radiation
作物蒸散是农田水循环的主要损失途径,其准确信息对灌溉系统设计运行、灌溉制度制订及农业用水管理具有重要意义。尽管蒸散量可以直接测定,但费时费力,且仪器昂贵,目前多限于科研中小范围使用,实际应用中多采用估算法,特别是基于参考作物蒸散量(ET0)和作物系数的计算方法[1]。因此,ET0的计算是准确估算蒸散量的关键。
参考作物蒸散量 (ET0)指水分供应充足的参照作物表面的蒸散速率[1]。ET0概念由 Penman[2]和Thornthwaite[3]的潜在蒸发演变而来,于20世纪70年代中后期在FAO 24[4-5]首次引入。后来美国的Jensen 等[6]将计算潜在蒸发的所有方法,如 Priestley-Taylor (PT)[7]、Blaney-Criddle[6]、Turc[8]、Hargreaves[9]等均纳入ET0范畴。ET0的物理意义代表大气蒸发需求,反映了气象因素对作物需水的影响。
常用的参照作物有草和苜蓿两种。尽管苜蓿的特性更接近农作物,但对苜蓿的试验资料较少;而由于气象站观测均以草为下垫面,故草作为参照作物应用更广[10],苜蓿在美国有少量应用。FAO 56[1]把参照作物描述为一种具有固定特性的假想作物(a hypothetical crop)。国外学者[6, 11]通常把试验测定的冷型草蒸散量作为ET0真值,并作为标准检验其它方法。
以往已提出很多ET0方法,大致可划分为温度法[3,9]、辐射法[7-8, 12]、道尔顿(Dalton)[13]法(也称质量传输法或空气动力学法)、综合法[2, 14-15]和蒸发皿法[5]等类型,每一类型方法中又有若干方法,十分繁杂。由于气候的多样性及复杂性,加之对各类方法缺乏系统检验,实际中难以做出合理选择。因此,不同ET0方法的评价一直是蒸散理论研究的重要内容。
虽然已有不少 ET0评价研究报道,但大多[16-19]以FAO56 PM为标准,国内尤其如此。然而,FAO56 PM是否在各种气候条件下均最准确仍有争议。Steduto等[20]使用 7个地中海气候类型国家的实测数据研究了FAO56 PM的准确性,发现其严重低估,估算标准差SEE 为0.84~2.60mmd-1。De Bruin等[10]在荷兰使用波文比实测值比较了 6种法,发现当所有变量均实测时,1956 Penman式和PT公式表现最好,与实测值的比值为1.01,斜率=1.01,决定系数R2=0.88,而FAO56 PM与实测的比值为1.14,斜率=1.13,R2=0.86。Howell等[11]使用称重式蒸渗仪在美国 Texas的研究也得出类似结论,即1948 Penman式好于FAO56 PM,比后者具有较高的R2和较低的SEE。Irmak等[21]使用波文比实测值比较了15 个ET0公式,尽管其结果认为ASCE-PM、1963和1948 Penman估算结果最接近实测值,但仔细分析发现,表现最好的前3个模型依次为PT (RMSE= 1.19mm ∙d-1),FAO24辐射模型(RMSE=1.27mm∙d-1)及1963 Penman (RMSE=1.31mm∙d-1),而2005 ASCE-PM排位第四,相应的RMSE=1.37mm∙d-1。使用20个涡度通量站点数据的最新研究[22]表明,FAO56 PM表现较差,在很多情况下低估,相应Nash- Sutcliffe效率系数(0.26)比PT (0.59)的小,而RMSE (105W∙m-2)却比PT(66 W∙m-2)的大。可见,以FAO56 PM为标准的评价研究结果可能存在较大不确定性。
称重式蒸渗仪是获得实测 ET0最好的方法之一,但其价格昂贵、不易维护,造成基于其实测值的评价研究世界范围内缺乏,目前多数来自美国[6, 11,23- 24]和地中海地区[20, 25-26]。而中国国内的系统研究几乎空白,现有结果尚不足以准确回答“中国气候条件下哪个或哪些ET0模型估算大气蒸发需求最准确”这一科学问题,不利于水资源管理水平和作物用水效率的提高,与中国农业水资源严重短缺的现实也不匹配。据此,本文使用称重式蒸渗仪试验观测的ET0,在北京昌平小汤山半干旱气候下检验16个复杂程度不同的模型,以便更好地指导农业灌溉和水资源管理。
1 材料与方法
1.1 ET0的观测
田间试验区位于北京市昌平区小汤山镇的国家精准农业试验示范基地内,试验基地面积167hm2。站点位于40.18°N、116.43oE,海拔36m,属大陆性季风气候,四季分明,光照充足。多年平均降水量574mm,主要分布在6-8月,占全年总降水的77%。多年平均气温12.1℃,其中最冷的l月为-4.1℃,最热的7月为25.7℃。多年平均日照时数2641h,无霜期约200d。试区土壤为潮土,0-0.5m土层平均田间持水率(体积含水率)为0.37cm3∙cm-3。
参照国际通用做法,供试参照作物采用禾本科冷季型草坪草高羊茅(Festuca arundinacea Schreb),于2011年8月12日播种,播种量30g×m-2,至2012 年4月生长基本稳定。用2台称重式蒸渗仪(西安产)测定草坪蒸散量。蒸渗仪长×宽×高=1.3m×1.3m×2.3m,内装 2m原状土,底部为 0.3m沙土过滤层,测量精度为0.01mm。蒸渗仪内安装一支负压计(SoilSpec,澳大利亚产)监测土壤水分变化,埋深0.2m,当土壤水势降至-20kPa时(相当于田间持水率的 66%)启动喷灌灌水,直至土壤水势达到-0.03~0kPa。与蒸渗仪相连接的电脑记录土壤重量变化,且每隔 10min采集一次数据。蒸渗仪及高羊茅草的详细描述见文献[27]。
试验数据采用2012年4-10月的测定结果。一日内每10min水分损失的累加值为日ET0观测值。为保证数据质量,剔除有降水、灌水、仪器故障日的测定值,质量控制后剩余168d的数据,2台蒸渗仪观测结果的平均值作为ET0实测值。
1.2 ET0计算模型
选择16种常用模型,包括5种综合法,即FAO56PM、1996 Kimberly Penman、FAO79 Penman、FAO 24 Penman及1963 Penman;6种辐射法,即Makkink、FAO24辐射模型、Priestley-Taylor、Debruin-Keijman、Jensen-Haise及Turc模型;5种温度法,即Hargreaves、 Hamon、Mcloud、FAO24 Blaney-Criddle及初始的Blaney-Criddle。每个模型的简称及计算公式见表1,计算式多取自Jensen等[6],少数参考了其它文献,不做详细介绍。

表1 评价模型及其计算式Table 1 The ET0models evaluated and their equations
1.3 气象数据及评价指标
在距蒸渗仪100m处安装Dynamet自动气象站(美国产)。采集要素包括最高与最低气温、最高与最低空气相对湿度、太阳总辐射、日照时数、降水量和 2m高度风速。数据采集间隔为10min,处理后生成日数据,可满足所有模型计算ET0的需求。主要使用4种统计指标评价ET0计算值与实测值的差异程度,包括决定系数(R2)、平均偏差(MBE)、均方根误差(RMSE)、t统计量,详细计算方法参阅文献[28]。
2 结果与分析
2.1 综合法模型计算值与实测值的比较
图1a-图1e表明,综合法模型估算的日ET0与蒸渗仪实测值呈极显著正相关(P<0.01),其R2为0.636~0.671。其中FAO79 Pen的估算值与实测值相关性最好,FAO56 PM最差。综合法模型估算的日ET0总体低于实测值,图1a-图1e中回归趋势线均位于 1:1线之下,由表 2可见,其估算与实测值的MBE<0,均表明低估的特点。5个模型的 MBE在-0.46~0.32mm∙d-1,平均-0.14 mm∙d-1。其中FAO24 Pen和FAO56 PM低估最大,FAO79 Pen高估最大。
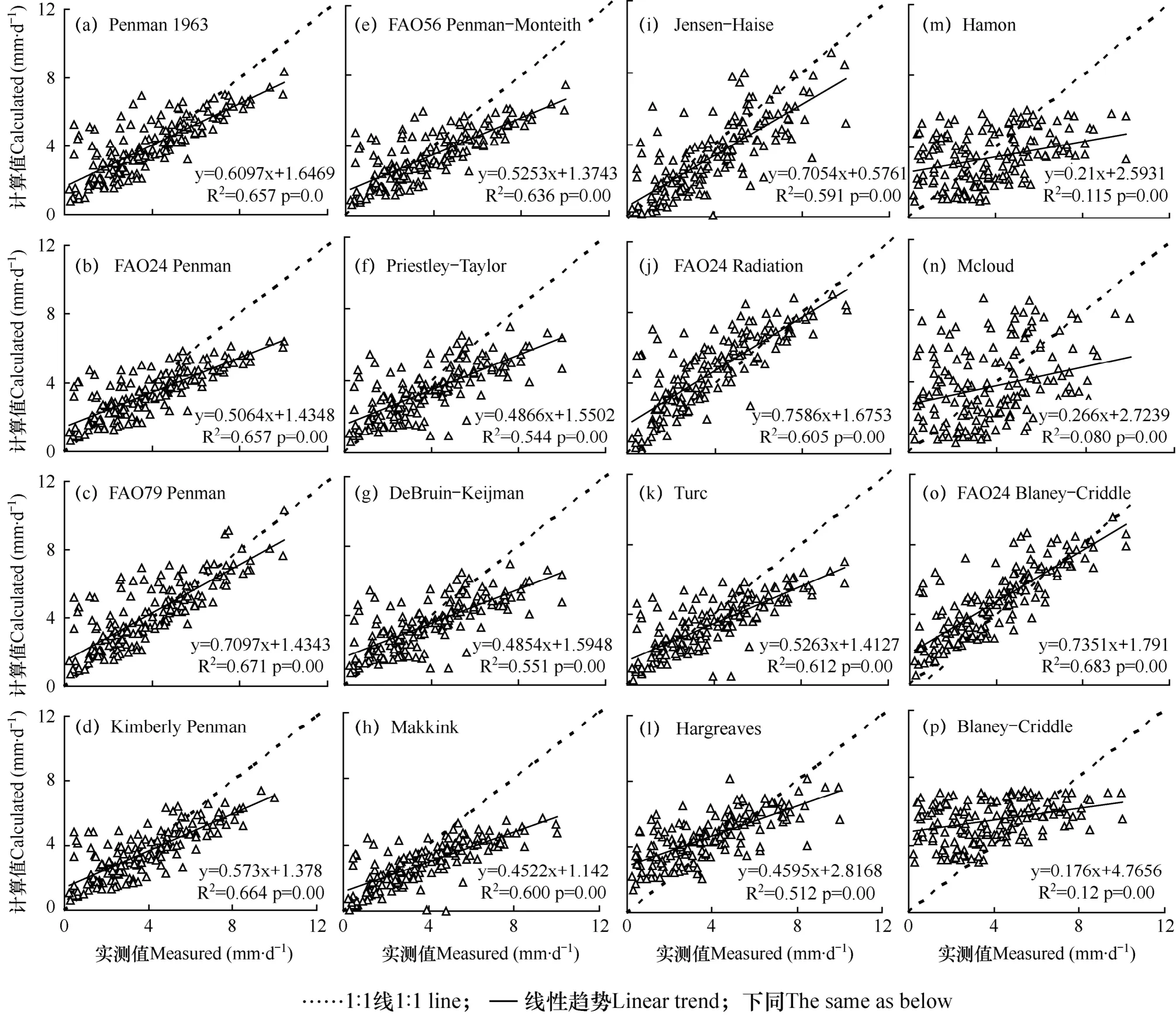
图1 模型计算的ET0日值与实测值的比较(n=168)Fig. 1 Comparison of calculated daily ET0against the measured value(n=168)
由图1a-图1e还可见,不同模型高估与低估之间的临界点存在差异,其中Pen63和FAO79的临界点较高,分别为4.22mm∙d-1、4.94mm∙d-1。低于这些临界值,模型估算值比实测值大,否则比实测值小。其它模型的临界值则较低,为2.90~3.23mm∙d-1,表明在大气蒸发力高的气象条件下使用这些模型将产生较大误差。
综合法模型估算值与实测值的RMSE为1.33~1.47mm∙d-1(表2),平均1.39mm∙d-1。依据RMSE,各综合模型的估算效果排序为FAO79 Pen=Pen63>KP>FAO24 Pen>FAO56 PM。可见,FAO79 Pen和Pen63表现同样好,与最差的FAO56 PM相比精度高10%。t检验(表 2)表明,FAO79 Pen、Pen63和KP的日估算值与实测值无显著差异(t<t0.05),进一步说明FAO79 Pen与Pen63表现一样好。
逐月日均值比较(图2)表明,综合法的估算值与蒸渗仪实测值变化趋势一致(图2a)。峰值均在5月,Pen63、FAO24 Pen、FAO79 Pen、KP和FAO 56 PM分别为5.31、4.40、5.90、4.71和4.47mm∙d-1,实测的峰值为5.44mm∙d-1。其中Pen63峰值与实测峰值最接近,比后者平均低0.14mm∙d-1;其次为FAO79 Pen峰值,比实测峰值平均高0.45mm∙d-1。FAO 56 PM和FAO24 Pen严重低估峰值,分别为0.97、1.04mm∙d-1。
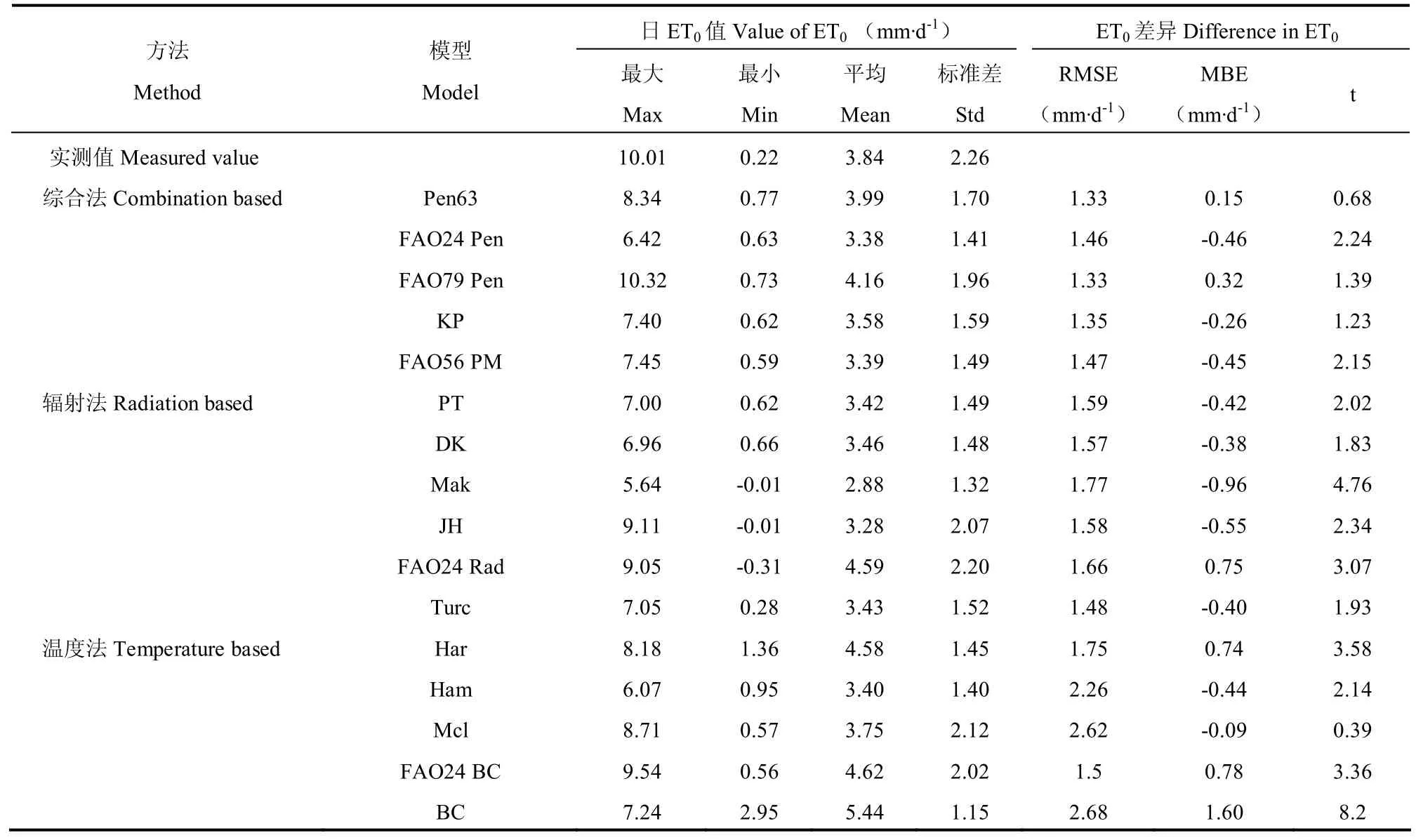
表2 模型估算值与实测ET0日值比较的统计特征值(观测样点=168)Table 2 Summary of statistics for daily ET0comparison between model estimates and lysimeter measurements (data points=168)
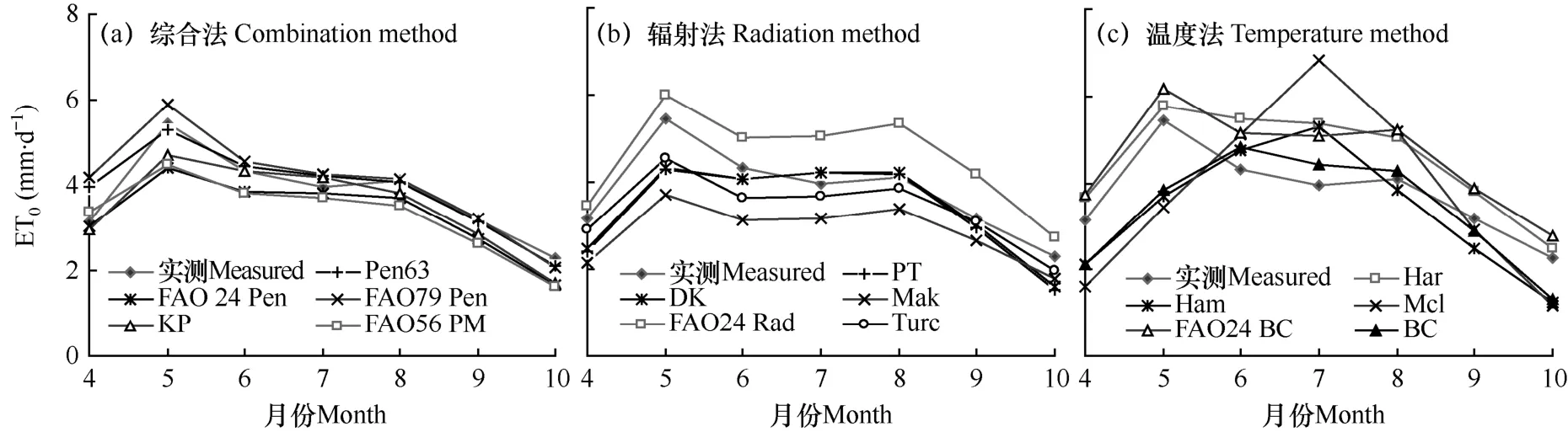
图2 模型估算值与实测逐月ET0日均值的比较Fig. 2 Comparison of monthly mean daily ET0between model calculation and lysimeter measurement
2.2 辐射法模型估算值与实测值的比较
由图1f-图1k可见,辐射法模型估算的日ET0与实测值也呈极显著正相关(P<0.01),但其R2比综合法低,在0.544~0.612。其中Turc的R2最大,PT的 R2最小。与综合法类似,辐射法估算的 ET0总体低于实测值。表2和图2b表明,除FAO24 Rad外,所有辐射模型均低估实测值,其MBE在-0.96~0.75mm∙d-1,6个模型平均为-0.33mm∙d-1。其中Mak低估最大,FAO24 Rad高估最大。
辐射模型同样具有低蒸发力下高估、高蒸发力下低估的特点(图1f-图1k),但高估与低估之间的临界值差异明显。其中 FAO24 Rad临界值最高(6.94mm∙d-1),当大气蒸发力低于此值时,估算值大于实测值,否则小于实测值。PT、DK、Turc的临界值类似,为2.98~3.10mm∙d-1。Mak和JH的临界值较低,为2.08、1.96mm∙d-1。显然,除FAO24 Rad外,其它辐射模型更适于低蒸发力条件,反之会产生较大误差。
依据RMSE(表2),各辐射模型的估算效果排序为Turc>DK>JH>PT>FAO24 Rad>Mak,相应的RMSE为1.48~1.77mm∙d-1,平均1.61mm∙d-1。其中DK、JH和PT 3个模型RMSE差异很小,在0.02mm∙d-1之内,说明三者表现类似。表现最好的Turc比最差的Mak和常用的PT模型精度分别高20% 和7%,但比最好的综合法FAO79 Pen模型精度低10%。辐射模型日估算值与实测值差异显著(t>t0.05,表2),因此,日尺度应用时需要校正。
与综合法类似,辐射模型估算值与实测值变化趋势一致(图2b)。其峰值均在5月,PT、 DK、Mak、JH、FAO24 Rad和Turc的峰值分别为4.28、4.33、3.70、4.47、5.99和4.53mm∙d-1。其中FAO24 Rad与实测峰值最接近,比后者平均高0.55mm∙d-1;其次为Turc,比实测峰值低0.91mm∙d-1;Mak在峰值月份低估最大,为1.74mm∙d-1。
尽管辐射法中PT应用最广,且有研究认为其精度较高[22],但在本研究中表现一般,与DK、JH精度类似。相比之下,Turc模型表现最好,这可能与该模型建立时使用了全球各地较多站点的数据有关,也可能是由于公式中含有额外变量T。Jensen等[6]也发现湿润气候下Turc好于PT;Yoder等[24]在美国一个湿润地点的研究得到类似结论,Turc在8个模型中排第3。
2.3 温度法模型估算值与实测值的比较
温度模型估算的日ET0与实测值也呈极显著正相关(P<0.01),但模型间R2差异较大,在0.080~0.683(图1l-图1p)。其中FAO24 BC的R2最高,Mcl的R2最低。与综合、辐射法不同,温度模型估算值总体大于实测值(图2c、表2),除Ham和Mcl外,其它模型均高估。其MBE在-0.44~1.60mm∙d-1,5个模型平均0.52mm∙d-1,其中BC高估最大,Har和FAO24 BC高估程度类似。温度模型在7、8月高估最大 (图2c),如Har和FAO24 BC的MBE为1.40、1.12mm∙d-1。刘晓英等[18]在华北以 FAO56为标准的研究表明,夏季各月Har计算值偏高,与本文结果一致。
由图1l-图1p可见,温度模型同样具有低蒸发力下高估、高蒸发力下低估的特点。高、低估的临界值因模型而异,其中Har、FAO24 BC和BC的临界值较高,在5.21~6.82mm∙d-1;Ham和Mcl临界值相对较低,为3.28、3.71mm∙d-1。与综合法和辐射法不同,温度法估算精度高的区域位于 ET0相对高值区,说明更适宜在较高蒸发力条件下使用。
由表 2可见,温度模型的 RMSE在 1.50~2.68mm∙d-1,平均2.03mm∙d-1。依据RMSE,各温度模型的估算效果排序为 FAO24 BC>Har>Ham>Mcl>BC。表现最好的FAO24 BC比最差的BC和常用的Har精度分别高78%和16%,但比最好的综合模型FAO79 Pen低13%,与最好的辐射模型Turc相差较小。t检验显示(表2),温度模型估算值与实测值差异显著(t>t0.05)。
图2c显示,温度模型估算值与实测值变化趋势吻合性差异较大。其中Har和FAO24 BC与实测值趋势一致,峰值(5.77、6.16mm∙d-1)均在5月,表明结构合理,通过参数校正即可改善精度。其余模型估算值与实测值趋势不一致,峰值在 7月,为5.30~6.84mm∙d-1,表明结构不合理,通过结构优化有较大改进空间。
尽管Har远比FAO24 BC应用广,但比后者精度低16%。虽然二者估算值与实测值变化趋势一致,但由于其持续高估(图 2c),导致与实测值差异显著。BC模型基于美国20世纪20-30年代大量土壤水分平衡数据于1942年建立,之后经过多次改进,在美国西部应用较广。作为BC修正式,FAO24 BC虽看起来很简单,仅含气温一个变量,但实际上其参数a、b却隐含其它要素的复杂影响(表1),其良好表现可能与此密不可分。FAO24 BC隐含的复杂性,使之失去了温度法低数据需求的重要优点,这可能是导致其不如Har应用广泛的主要原因。
可见,三大类ET0方法具有两个共同点。首先,所有模型估算值与实测值均极显著相关,但R2差异较大(图1),其中综合法的R2总体最大,辐射法次之,温度法最小。其次,所有模型均在低蒸发力下高估、高蒸发力下低估,呈现阈值特点。综合法、辐射法模型的共同点较多:二者的估算值与实测值变化趋势一致,但温度法仅Har和FAO24 BC与实测值趋势一致(图2);二者的ET0高、低估临界值比温度法低(图1),故更适于低蒸发力条件,而温度法更适于高蒸发力条件;二者的计算值在4-10月平均偏低 0.14、0.33mm∙d-1,而温度法平均偏高0.52mm∙d-1(表2)。
所有模型依据 RMSE的精度排序为 FAO79 Pen=Pen63>KP>FAO24 Pen>FAO56 PM>Turc>FAO24 BC>DK>JH>PT>FAO24 Rad>Har>Mak >Ham>Mcl>BC。总体而言,综合法日值估算精度最高,辐射法次之,温度法最低。但也并非绝对,如FAO24 BC不仅在温度法中表现最好,而且超过了5个辐射模型。Jensen等[6]也发现,FAO24 BC在评价的13个模型中排第3,超过5个综合模型和所有辐射模型。Irmak等[21]也有类似研究结论,认为FAO24 BC是最好的非综合法模型(RMSE=0.64mm∙d−1)。
尽管许多研究[6, 24]指出FAO56 PM表现最好,但其在本研究中表现较差,仅与FAO24 Pen和Turc精度类似。本文结果大致支持Howell等[11]、Steduto 等[20]、Irmak[21]、Ershadi等[22]、Berengena等[25]的结论,即FAO56 PM并非在所有气候条件下均估算最准确。
2.4 偏差原因分析
将估算值绝对日偏差与气象变量作相关分析(图3)表明,VPD和RHx是影响综合模型偏差的两大主要因子。VPD对FAO24 Pen、KP、FAO56 PM的偏差影响最大,相关系数在 0.41~0.53,且 VPD越高,估算的偏差也越大。而RHx对Pen63、FAO79 Pen的偏差影响最大,相关系数在-0.44~-0.41;且RHx越大,估算偏差越小。u2对两个模型偏差影响也较大,相关系数在0.40~0.43。显然,低估类与高估类综合模型偏差的主要影响因子不同,前者为VPD,后者为RHx。
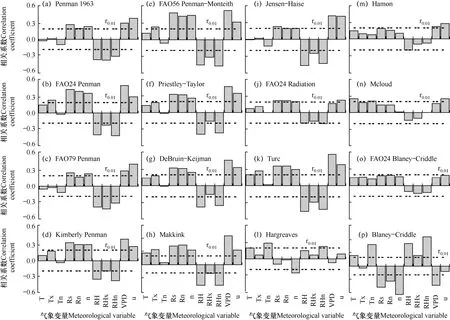
图3 模型估算值绝对日偏差与气象变量的相关性(n=168)Fig. 3 Correlation of absolute bias error for model estimates with meteorological variable (n=168)
同样,VPD也是影响辐射模型偏差的最主要因子。PT、DK、Mak和Turc的偏差均与VPD相关性最高,相关系数在0.46~0.65,且偏差随VPD增加而变大。但影响JH和FAO24 Rad偏差的主要因子分别为RH和u2,相关系数分别为-0.46、0.23。
温度法不同模型的偏差影响因子差异较大,如Har为Tn,Ham为u2,Mcl为u2和Tn,BC 为RHn。但所有气象要素对FAO24 BC偏差的影响均不显著,说明其已充分考虑了各要素间的相互作用,进一步改进空间不大。这与其良好的表现相一致。
相关分析(表3)表明,影响ET0的关键因子为VPD、Rs及 Rn,相关系数在 0.75~0.78。综合法、辐射法之所以好于温度法,是因为均显含这些因子(表1)。由于Rs或Rn与VPD具有较高的相关性,其相关系数分别为0.69、0.67,即辐射与VPD不相互独立,故仅考虑辐射的辐射法也表现良好。相比之下,温度法多使用T为变量(表1),但ET0与T的相关系数仅为0.37,而与Tx的相关系数为0.54。可见,多数温度模型并没有抓住影响 ET0的关键因子,这也是其表现差的原因。

表3 蒸渗仪实测值与气象要素的相关系数(观测样点=168)Table 3 Correlation coefficient of lysimeter measured ET0with meteorological variables (data points=168)
2.5 FAO56 PM表现差的原因分析
所有的 Penman类公式都间接假设表面阻力 rs为 0,空气动力阻力则隐含在风函数中。尽管一般认为 rs和空气动力阻力的引入是 Monteith[15]对Penman式的重要发展,但rs本身的经验成分及其准确表达问题,可能影响FAO56 PM的精度。其低估可能意味着采用 rs=70s∙m-1偏大。试算表明,当 rs由0增至60s∙m-1时RMSE为非线性变化(图4),且rs=40、50s∙m-1时RMSE最小,为1.45mm∙d-1(图4f-图4g)。尽管这一精度稍好于rs=70s∙m-1,但并无显著改善,故rs取值70s∙m-1与FAO56 PM表现差关联性不强。

图4 改变表面阻力对FAO56 PM日计算值的影响(n=168)Fig. 4 Effect of varying surface resistance on daily estimates of FAO56 PM (n=168)
FAO56 PM 低估问题以往也有报道[20, 22, 25]。Steduto等[20]指出,FAO56 PM在高蒸发力站点显著且持续低估实测值,并提出两点改进建议,其中之一是使用变化的rs取代固定值。但后来Lecina等[29]的研究并不支持此观点,因为变化的 rs虽对精度有所改善,但与阻力模型校正付出的工作量不匹配,因此使用固定的 rs足已。Ventura等[23]指出,rs从70s∙m-1降至42s∙m-1提高了PM的小时估算精度。显然,rs的合理参数化仍有争议。
辐射与空气动力项之间不合理的权重可能是FAO56 PM表现差的另一原因。如图5所示,空气动力项权重较高的综合模型估算精度也较高,如表现最好的FAO79 Pen和Pen63,4-10月空气动力项与ET0的比例在 0.19~0.48,比 FAO56 PM 的比例(0.10~0.47)明显偏高。特别在8-10月,该比例差异最大,FAO56 PM仅为0.10~0.28。因此,该模型表现差的部分原因是由于空气动力项权重相对较低,而在本研究地点气候条件下其具有重要作用,因为实测ET0与VPD相关性最高(表3)。
为进一步分析FAO56 PM表现差是偶然结果还是地域气候影响,表 4列出了试验期间逐月气象条件。根据降水量与ET0的比值(P/ET0),观测期间最小的是5、10、8月,相应的低估也几乎最严重,为14%~28%(表5);相反,最湿润的7月(P/ET0=2.32)低估最小,为6.5%。可见,FAO56 PM较差的表现与气候干燥程度有关。
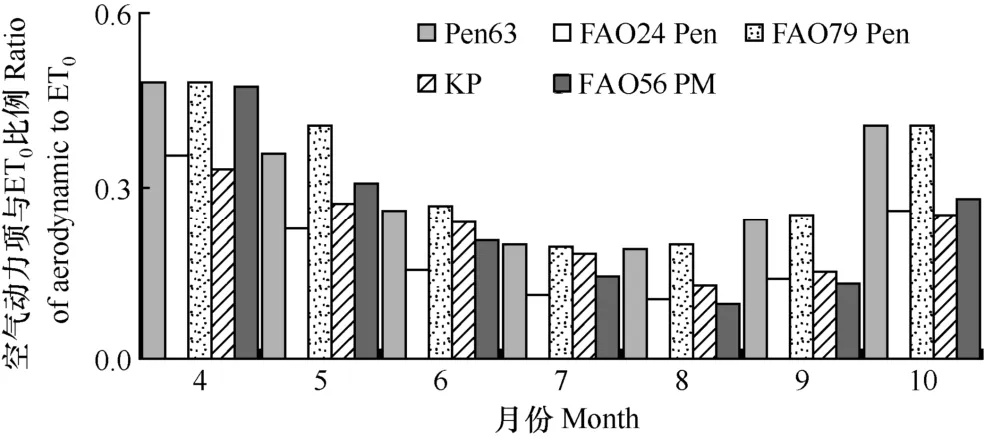
图5 综合法模型空气动力项与ET0的比例Fig. 5 Ratio of aerodynamic component to ET0for combination models

表4 试验观测期间逐月平均气象条件Table 4 Monthly meteorological condition in experiment period

表5 模型估算值与蒸渗仪实测值的逐月平均日差异(%)Table 5 Monthly mean daily differences(%)in ET0between estimates of combination models and lysimeter measurements
早在1991年FAO的咨询报告[30]就指出,考虑到 Penman法的历史价值及众多用户,应当有足够的证据来证明FAO PM确实比Penman法优越。遗憾的是,尽管目前FAO56 PM广泛使用,但并未被广泛验证,故仍有必要使用实测值检验以明确该模型是否真正比综合法其它模型优越。特别在中国,FAO56 PM推荐前FAO79 Pen及Pen63广泛使用,积累了大量作物系数及需水量信息。由于作物系数与使用的 ET0方法紧密关联,ET0公式的转变,也意味着基于其它ET0方法的相关知识要随之更新,造成额外资源投入。目前国内许多基于FAO56 PM的作物系数研究[31-32],显然是向这一公式转变的体现。但根据本研究结果,这些工作是否真正必要值得质疑。
2.6 常用模型的参数校正
为提高常用模型的估算精度,对辐射模型 PT、Mak和Turc的原系数1.26、0.63和0.013进行校正。将使用日值校正得到的所有系数平均后作为模型系数。与原系数相比,3个模型的校正系数均增加,分别为1.38、0.83、0.014,但Turc的系数变化不大。相关分析表明,校正系数与RH、RHn、VPD呈极显著相关(P<0.01,图 6),且与前二者为负相关,与VPD为正相关。最低温度Tn与PT系数也存在极显著相关性。显然,RHn对PT的系数影响最大(图6a),而VPD对Mak、Turc的系数影响最大(图6b、6c)。
作为Penman公式的简化式,PT模型略去了空气动力项的显式影响,但增加了经验系数 α来考虑平流影响。Priestley等[7]发现α=1.26适于自由水面或供水良好的植被冠层,表明平流影响为辐射项的26%。但这一比例可能不适合干旱气候,较高的α似乎更合适,如α=1.7~1.75[6]或α=1.35~1.67[16]。这是因为干燥气候下有更多干空气流向灌溉植被,导致平流作用加大,因此α相应增加。据此,本文校正的α大于原系数是合理的。但国内一些学者[33-34]使用实际蒸散量校正PT系数,因此得到的α多小于1.26。
对温度法模型Har、Ham和BC的系数0.0023、0.55和0.46的校正显示,Har和BC的校正系数比原系数减小,为 0.0019、0.192,而 Ham的系数增至1.248。校正的日系数与Rs、n、RH、RHn及VPD呈极显著相关(P<0.01,图7)。其中Har和BC模型系数与Rs或n的相关性最好 (图7a、7c),而Ham模型参数与RHn的相关性最好(图7b)。国内对Har模型的校正多以FAO56 PM为标准,但校正系数仍低于原系数 0.0023[35]。这与本文使用称重式蒸渗仪校正的结果趋势一致。
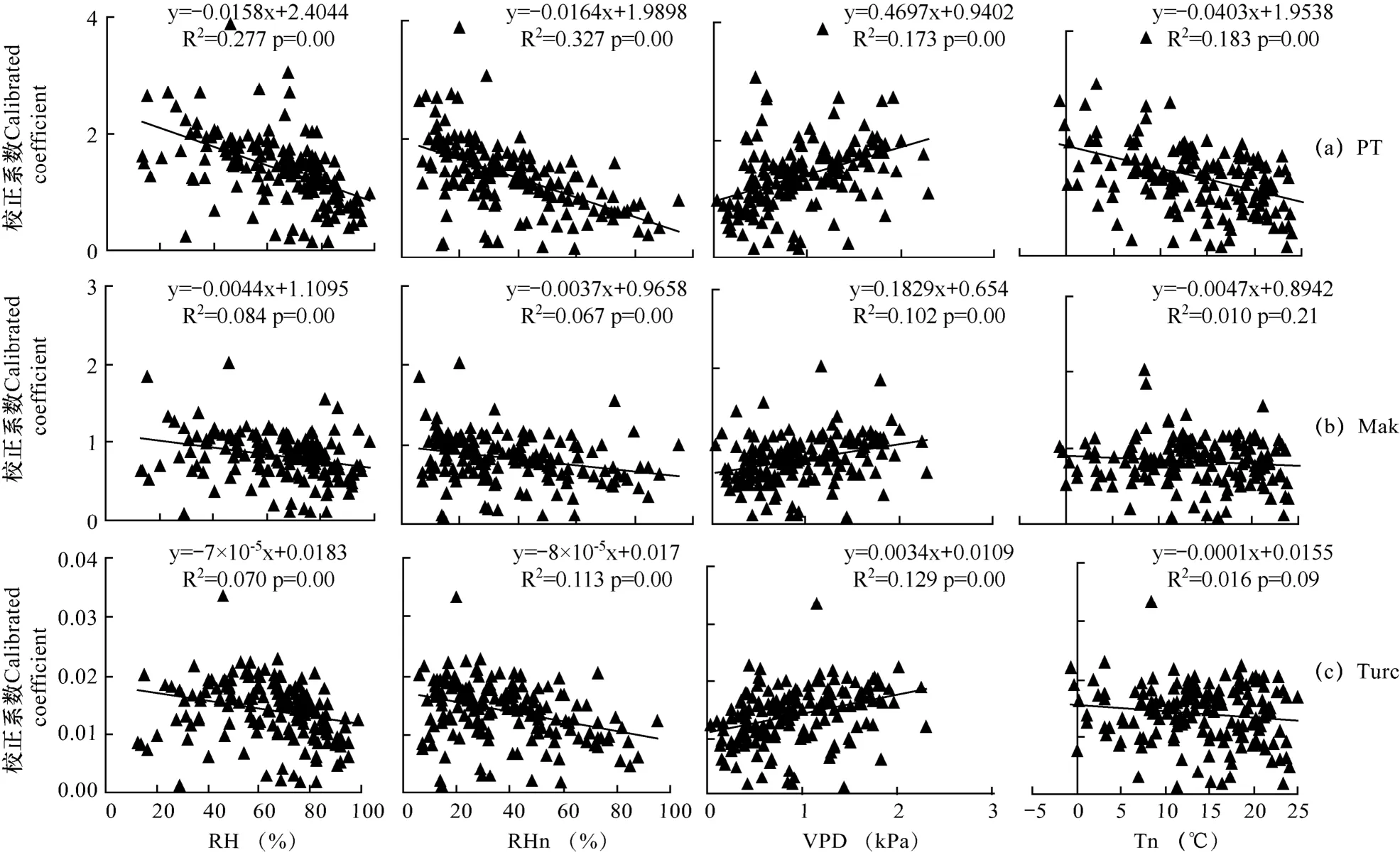
图6 辐射法校正的日参数值与气象要素的关系(n=168)Fig. 6 Relations of calibrated daily coefficients for radiation models with meteorological variables(n=168)

图7 温度法校正的日值参数与气象要素的关系(n=168)Fig. 7 Relations of calibrated daily coefficients for temperature models with meteorological variables(n=168)
3 结论与讨论
在半干旱气候条件下使用称重式蒸渗仪实测ET0日值评价16个模型表明,综合法模型表现最好,其中FAO79 Pen和Pen63最好;其次为辐射法,以Turc最好;温度法表现最差,其中以FAO24 BC最好。3大类方法的 RMSE分别为 1.33~1.47mm∙d-1(平均 1.39mm∙d-1)、1.48~1.77mm∙d-1(平均1.61mm∙d-1)、1.50~2.68mm∙d-1(平均2.03mm∙d-1),其中后两类方法比综合法精度分别低16%和46%,而温度法比辐射法精度低 26%。综合法、辐射法的普适性之所以好于温度法,是因为均含有影响 ET0的关键因子(辐射或VPD),多数温度法则不含。
综合法、辐射法及温度法计算的ET0与蒸渗仪实测值的差异分别为-0.46~0.32mm∙d-1、-0.96~0.75mm∙d-1、-0.44~1.60mm∙d-1。前两类方法总体表现为低估,4-10月平均偏低0.14mm∙d-1和0.33mm∙d-1;而温度法以高估为主,平均偏高0.52mm∙d-1。
所有模型在低蒸发力下高估、高蒸发力下低估,呈现阈值特点。三大类模型高估与低估的阈值分别为 2.90~4.94mm∙d-1、1.96~6.94mm∙d-1、3.28~ 6.82mm∙d-1,且综合法、辐射法比温度法的ET0阈值低,说明前两类方法更适于低蒸发力条件,而后者适于高蒸发力条件。
综合模型结果的差异主要反映了风函数差异的影响。Pen63与FAO79 Pen估算精度同样好,表明Pen63及其风函数普适性好,同时说明对原始Penman式的诸多修正并没有显著改善精度。鉴于对Penman式的修正多集中在风函数,且对修正后的真正效果缺乏认识,有必要进一步系统研究。
FAO56 PM(RMSE=1.47mm∙d-1)在综合法中表现最差,模拟精度比FAO79 Pen和Pen 63低10%,但在最湿润的7月表现最好,平均低估6.5%。表现差的主要原因在于研究站点干燥的气候及相对较低的空气动力项比例。改变表面阻力不能有效提高精度。
综合法、辐射法及温度法的Har与FAO24 BC计算值与实测值变化趋势一致,表明其结构合理,今后精度改善的重点在于参数校正。对于与实测值变化趋势不一致的温度模型,其结构本身存在问题,改进重点在于优化结构。
VPD和RHx是造成综合法、辐射法计算偏差的两大主要因子。其中低估类模型的主要因子为VPD,且VPD越高,低估偏差也越大;而高估类的综合模型(Pen63、FAO79 Pen)其主要因子为RHx,且RHx越大,高估偏差越小。温度模型估算偏差的影响因子较复杂,模型间差异很大,但影响 Har偏差的最大因子为Tn。
常用的辐射及温度模型在与本研究站点类似的气候下使用需要校正。PT、Mak、Turc和Ham的系数需要分别增至1.38、0.83、0.014、1.248,而Har、BC系数则需减至0.0019、0.192。这些系数也可由气象变量估算,其中PT、Ham的系数使用RHn能得到最佳估算,Turc、Mak的系数使用VPD、Har,BC的系数使用Rs或n均能得到最佳估算。
鉴于FAO56 PM在本研究中表现不佳,同时考虑到其作为检验标准的重要作用,以及国内外众多基于此模型的作物系数研究,使用实测值进一步检验对回答诸如“FAO56 PM 是否真正优于老版本Penman式”、“在何种气候条件下表现好”、“高蒸发力条件下低估是否为普遍现象”等科学问题具有重要价值。
References
[1]Allen R G,Pereira L S,Raes D,et al.Crop evapotranspiration: guidelines for computing water requirements[M]. Rome: FAO,1998.
[2]Penman H L.Natural evaporation from open water,bare soil and grass[J]. Proc of the Royal Soc(Series A),1948,193: 120-145.
[3]Thornthwaite C W.An approach toward a rational classifycation of climate[J].Geogr Rev,1948,38:55-94.
[4]Doorenbos J,Pruitt W O.Guidelines for predicting crop water requirements [M].Rome:FAO,1975.
[5]Doorenbos J,Pruitt W O.Crop water requirements[M]. Rome: FAO,1977.
[6]Jensen M E,Burman R D,Allen R G.Evapotranspiration and irrigation water requirements[M].New York:ASCE,1990.
[7]Priestley C H B,Taylor R J.On the assessment of surface heat and evaporation using large-scale parameters[J].Mon Weather Rev,1972,100:81-92.
[8]Turc L.Evaluation des besoins en eau d’irrigation, evapotranspiration potentielle,formule climatique simplified et mise a jour[J].Ann Agron,1961,12(1):13-49.
[9]Hargreaves G H,Samani Z A.Reference crop evapotranspiration from temperature[J].Applied Engineering in Agriculture,1985,1(2):96-99.
[10]De Bruin H A R,Stricker J N M.Evaporation of grass under non-restricted soil moisture conditions[J].Hydrological Sciences Journal,2000,45(3): 391-406.
[11]Howell T A,Evett S R,Schneider A D,et al.Evapotranspiration of irrigated fescue grass in a semi-arid environment[J]. USA:ASAE,1998.
[12]Makkink G F.Testing the Penman formula by means of lysimeters[J].J Inst Water Eng,1957,11(3):277-278.
[13]Dalton J.Experimental essays on the constitution of mixed gases;on the force of steam or vapor from water and other liquids in different temperatures,both in a Torricellian vacuum and in air;on evaporation and on the expansion of gases by heat[C].Mem.Manchester Liter.and Phil.Soc., 1802: 5-11,535-602.
[14]Penman H L.Vegetation and hydrology[M]. Harpenden, England: Tech. Comm.No.53,Commonwealth Bureau of Soils, 1963.
[15]Monteith J L.Evaporation and environment[M]. Cambridge: Cambridge University Press,1965,19:205-234.
[16]Castellvi F,Stockle C O,Perez P J,et al.Comparison of methods for applying the Priestley-Taylor equation at a regional scale[J].Hydrol Process,2001,15:1609-1620.
[17]曹金峰,李玉中,刘晓英,等.四种参考作物蒸散量综合法的比较[J].中国农业气象,2015,36(4):428-436. Cao J F,Li Y Z,Liu X Y,et al.Comparison of four combination methods for reference crop evapotranspiration [J].Chinese J Agrometeorol,2015,36(4): 428-436.(in Chinese)
[18]刘晓英,李玉中,王庆锁.几种基于温度的参考作物蒸散量计算方法的评价[J].农业工程学报,2006,22(6):12-18. Liu X Y,Li Y Z,Wang Q S.Evaluation on several temperature- based methods for estimating reference crop evapotransp- iration[J].Transactions of the CSAE,2006,22(6): 12-18.(in Chinese)
[19]樊军,邵明安,王全九.黄土区参考作物蒸散量多种计算方法的比较研究[J].农业工程学报,2008,24(3):98-102. Fan J,Shao M A,Wang Q J.Comparisons of many equations for calculating reference evapotranspiration in the Loess Plateau of China[J].Transactions of the CSAE,2008,24(3): 98-102.(in Chinese)
[20]Steduto P,Caliandro A,Rubino P,et al.Penman-Monteith reference evapotranspiration estimates in the Mediterraneanregion[A].In Camp C R,Sadler E J,Yoder R E(Eds), Evapotranspiration and Irrigation Scheduling[C].San Antonio,Texas: Proc Int’l Conf,ASAE,1996:357-364.
[21]Irmak A,Irmak S.Reference and crop evapotranspiration in south central Nebraska II:measurement and estimation of actual evapotranspiration for corn[J].J Irrig Drain Eng,2008, 134(6):700-715.
[22]Ershadi A,McCabe M F,Evans J P,et al.Multi-site evaluation of terrestrial evaporation models using FLUXNET data[J]. Agric Forest Meteorol, 2014,187:46-61.
[23]Ventura F,Spano D,Duce P,et al.An evaluation of common evapotrans-piration equations[J].Irrig Sci,1999,18(4): 163-170.
[24]Yoder R E,Odhiambo L O,Wright W C.Evaluation of methods for estimating daily reference crop evapotranspiration at a site in the humid southeast United States[J].Applied Engineering in Agriculture,2005,21(2): 197-202.
[25]Berengena J,Gavilán P.Reference evapotranspiration estimation in a highly advective semi-arid environment[J].J Irrig Drain Eng ASCE,2005, 131(2):147-163.
[26]López-Urrea R,Martín de Santa Olalla F,Fabeiro C,et al. Testing evapotranspiration equations using lysimeter observations in a semiarid climate[J].Agric Water Manage, 2006,85:15-26.
[27]袁小环,杨学军,陈超,等.基于蒸渗仪实测的参考作物蒸散发模型北京地区适用性评价[J].农业工程学报,2014, 30 (13):104-110. Yuan X H,Yang X J,Chen C,et al.Applicability assessment of reference evapotranspiration models in Beijing based on lysimeter measurement[J].Transactions of the CSAE,2014, 30 (13): 104-110.(in Chinese )
[28]Liu X Y,Xu Y L,Zhong X L,et al.Assessing models for parameters of the Ångström–Prescott formula in China[J]. Applied Energy,2012,96:327-338.
[29]Lecina S,Martínez-Cob A,Pérez P J,et al.Fixed versus variable bulk canopy resistance for reference evapotranspiration estimation using the Penman-Monteith equation under semiarid conditions[J].Agric Water Manage, 2003,60: 181-198. [30]Smith M,Allen R G,Monteith J L,et al.Report on the expert consultation on revision of FAO methodologies for crop water requirements [R].Rome: FAO Land and Water Development Division,1991.
[31]宋妮,孙景生,王景雷,等.基于 Penman修正式和Penman-Monteith公式的作物系数差异分析[J].农业工程学报,2013,29(19):88-97. Song N,Sun J S,Wang J L,et al.Analysis of difference in crop coefficients based on modified Penman and Penman-Monteith equations[J]. Transactions of the CSAE,2013, 29(19): 88-97.(in Chinese)
[32]刘安花,李英年,薛晓娟,等.高寒草甸蒸散量及作物系数的研究[J].中国农业气象,2010,31(1):59-64. Liu A H,Li Y N,Xue X J,et al.Study on evapotranspiration and crop coefficient of the alpine meadows in the Haibei Area[J]. Chinese J Agrometeorol,2010,31(1):59-64.(in Chinese)
[33]莫兴国.引入平流影响的蒸散发估算[J].生态农业研究, 1995, 12(3):49-53. Mo X G.Estimation of evapotranspiration by considering the advection effect[J]. Eco-Agriculture Research,1995,12(3): 49-53.(in Chinese)
[34]赵玲玲,王中根,夏军,等.Priestley-Taylor公式改进及其在互补蒸散模型中的应用[J].地理科学进展,2011,30(7): 805-810. Zhao L L,Wang Z G,Xia J,et al.Improved Priestley-Taylor method and its application in complementary relationship evapotranspiration model[J].Progress in Geography, 2011, 30 (7):805-810.(in Chinese )
[35]胡庆芳,杨大文,王银堂,等.Hargreaves公式的全局校正及适应性评价[J].水科学进展,2011,22(2):160-167. Hu Q F,Yang D W,Wang Y T,et al.Global calibration of Hargreaves equation and its applicability in China[J]. Advances in Water Science,2011,22(2):160-167.(in Chinese)
Evaluation of 16 Models for Reference Crop Evapotranspiration (ET0) Based on Daily Values of Weighing Lysimeter Measurements
LIU Xiao-ying1, LI Yu-zhong1, ZHONG Xiu-li1, CAO Jin-feng1, YUAN Xiao-huan2
(1.Institute of Environment and Sustainable Development in Agriculture, Chinese Academy of Agricultural Sciences/Key Laboratory of Dryland Agriculture, Ministry of Agriculture, Beijing 100081, China; 2.Beijing Research & Development Center for Grass and Environment, Beijing 100097)
Accurate estimation of reference crop evapotranspiration (ET0) is essential due to its critical role in determining crop water use and regional assessment of water supply and demand. Though numerous models have been developed, their rigorous test with measured data is lacking. In this paper daily estimates of 16 ET0models, including five combination-, six radiation- and five temperature-based ones, were evaluated with measurements from April through October in 2012 at a semiarid site of Xiaotangshan, Beijing, China. Daily ET0was measured by two weighing lysimeters (length×width×depth =1.3m×1.3m×2.3m) located in a fescue grass (Festuca arundinacea Schreb) plot surrounded by a 167ha crop. On basis of root mean square error (RMSE) we found the performance ranking: FAO79 Penman =1963 Peman>1996 Kimberly Penman>FAO24 Penman>FAO56 Penman-Monteith (PM)>Turc>FAO24 Blaney-Criddle(BC)>DeBruin-Keijman>Jensen-Haise>Priestley-Taylor (PT)>FAO24 Radiation>Hargreaves>Makkink>Hamon>Mcloud>Blaney-Criddle(BC). Overall, the combination models performed best with RMSE of 1.33-1.47mm∙d-1, followed by the radiation models with RMSE of 1.48-1.77mm∙d-1and the temperature models with RMSE of 1.50-2.68mm∙d-1. The best FAO79 Penman and 1963 Penman were respectively 10% and 13% more accurate than the best radiation (Turc) and temperature(FAO24 Blaney-Criddle)models. Better performance of the combination and radiation models was due to that they explicitly contain dominant factors(radiation or vapor pressure deficit(VPD))influencing ET0. All models tended to overestimate at low evaporative rate while underestimate at high rate the measured values, exhibiting threshold feature, but on average the combination and radiation methods respectively underestimated by 0.14mm∙d-1and 0.33mm∙d-1, whereas the temperature method overestimated by 0.52mm∙d-1. The former two had relatively lower threshold ET0than the latter, and they were thus more applicable to low evaporative condition, and vice versa for the latter. All combination and radiation models, and the Hargreaves and FAO24 BC in temperature method captured measurement trend and showed robust structure. To improve them future efforts should be on local calibration, but for temperature models not capturing measurement trend future focus should be on structure optimization. VPD and maximum humidity RHxwere two main factors affecting deviation of combination and radiation methods. The former affected models with underestimation in a positive manner, and the latter affected those with overestimation (1963 Penman、FAO79 Penman) in a negative manner. The calibrated coefficients of the PT (1.38), Makkink (0.83), Turc (0.014)and Hamon (1.248) were higher while those of the Hargreaves (0.0019) and BC (0.192) were lower than the original ones. Coefficients of PT and Hamon can also be best estimated with minimum humidity, and those of Turc and Makkink with VPD, and Hargreaves and BC with radiation or sunshine hours. The degree of climate dryness of the study site and the lower relative weight to the aerodynamic component were responsible for poor behavior (RMSE=1.47mm∙d-1) of the FAO56 PM. Later modifications to wind function of original Penman appeared fruitless, and therefore we suggest continued use of the older Penman equations in climate similar to our site in China. Meanwhile, more tests of the FAO56 PM against measurements would be valuable to answer questions like “Is the FAO56 PM really superior to the older Penman equations solely in terms of accuracy”, “in what climate it performs better” and “Is it common that it underestimates in high evaporative condition”.
Penman-Monteith; Priestley-Taylor; Turc; Hargreaves; Makkink; Blaney-Criddle; FAO24 radiation
10.3969/j.issn.1000-6362.2017.05.002
刘晓英,李玉中,钟秀丽,等.基于称重式蒸渗仪实测日值评价16种参照作物蒸散量(ET0)模型[J].中国农业气象,2017,38(5):278-291
2016-08-12
国家自然科学基金项目(41371065)
刘晓英(1964-),研究员,博士,主要从事农业节水研究。E-mail: liuxiaoying@caas.cn

