基于WITI的终端空域短期延误预测
张 明,张 明*,刘 凯,赵 敏
(1.南京航空航天大学民航学院,南京 211106;2.中国民用航空江苏安全监督管理局,南京 210022)
基于WITI的终端空域短期延误预测
张 明1,张 明1*,刘 凯1,赵 敏2
(1.南京航空航天大学民航学院,南京 211106;2.中国民用航空江苏安全监督管理局,南京 210022)
针对终端空域内短期天气条件变化引起的航班延误问题,首先利用雷达回波平面位置显示(PPI)和距离高度显示(RHI)对降水等级分类,通过图像识别方法对不同降水等级的云团进行轮廓提取;其次将对应时间的交通流信息与降水云团的空间范围匹配,提出了不同降水等级条件下的三维天气影响交通指数(WITI)计算方法;最后结合实际管制规则,将WITI指数与管制间隔调整和改航条件下的延误时间作指数回归分析,得到短期延误预测模型。通过算例仿真验证了该模型的拟合优度相比于线性回归模型提高了1.6%~4.3%,且估计标准误差趋近于0,说明指数回归延误预测模型更能反映天气影响下终端空域的实际延误状况。
终端空域;降水等级;交通流;WITI;延误预测
近年来,天气影响航班延误的问题一直受到国内外学者的广泛关注,对此展开了大量的研究工作。Callaham等[1]提出天气影响交通指数WITI概念,WITI指数可以反映天气对交通流的影响程度。Chatterji[2]和Sridhar[3]扩展了WITI的概念,并通过线性回归方法对美国空域系统的延误与WITI之间的关系建模。Klein等[4]结合航路WITI、终端区WITI和机场排队延误,提出NAS天气影响指数NWX,考虑天气、交通需求和机场排队等因素分析延误状况。Hansen等[5]对航班延误与交通流、机场天气、航路对流天气、天气预报的准确性等因素之间的关系建立延误分析模型。Klein等[6]基于协同对流天气预测产品CCFP建立了WITI预测模型,由于CCFP每2 h更新预报,更新频率比较低,而麻省理工学院林肯实验室开发的走廊综合气象系统(CIWS),每5 min的时间间隔可进行一次天气预报,更适用于短期延误预测。Sridhar等[8]根据CIWS提供的天气数据和ASPM提供的航班现在和过去的延误数据,利用未来空中交通管理概念评估工具FACET计算出WITI和预测WITI(P-WITI),利用线性回归模型预测美国空域系统未来2 h的延误。Chen等[9]利用CIWS提供的降水云团的位置和回波顶高等数据,结合航空器高度数据计算WITI指数,并利用自回归分析得到延误预测模型。Diana等[10]在终端空域天气影响条件下,利用整数规划模型动态调整终端空域进场路径,缓解空域拥塞,并验证了在实际天气影响下的适用性。Scot等[11]指出由于终端空域内的航空器间隔相对较小、稳定性不高,极易受到对流天气的影响,提出基于对流天气规避模型(CWAM)的对流天气影响预测模型,并提供5 h的影响预测。Ison[12]通过调研发现影响终端区延误的主要因素有天气条件、交通流需求以及航空器的进场路径等,且终端区应根据实际的运行条件和管制规则建立独有的延误预测模型。以往对天气影响下航班延误预测的研究大多利用天气影响交通指数WITI建立延误预测模型,而WITI指数与降水等级的划分阈值有关,并没有全面考虑不同降水等级条件下,结合不同的管制规则分析延误状况。此外,国外关于天气影响交通指数WITI与航班延误的关系问题大都针对国家空域网络层面,而针对终端空域的复杂天气引起延误的研究较少。
本文主要讨论终端空域在短期降水条件影响下的延误时间预测。首先通过雷达回波平面位置显示(PPI)和距离高度显示(RHI)图像的颜色划分降水等级,并识别不同降水等级的图像,提取轮廓以确定二维影响范围和降水云团的高度范围;其次提出三维天气影响交通指数WITI,运用WITI的计算方法统计不同降水等级条件下受影响航空器数量和管制规则不同产生的延误,利用指数回归分析建立短期延误预测模型;最后通过算例仿真验证在不同降水等级条件下的三维WITI指数计算方法以及延误预测模型的正确性。
1 降水等级分类
为了解恶劣天气对实际管制调配措施的影响,对管制员进行调研访问。当终端空域发生危险天气时,管制员将雷达回波图像与终端空域结构匹配,根据雷达回波图像呈现的颜色,判断恶劣天气对进场航段影响程度,调整管制间隔或飞行员申请改航,根据管制间隔以及改航路径的不同,航班延误时间也有所差异。
目前,国内终端区的天气预报产品主要是多普勒气象雷达,利用多普勒效应来测量云和降水粒子相对于雷达径向运动速度,显示方式有PPI和RHI。根据目标对雷达波的反射率对应降水云团中水滴的直径,水滴直径越大,该降水云团的雷达回波就越强,从而显示出不同的色调[13]。根据雷达回波图像中不同颜色的分布来判断降水强度的大小。降水等级、颜色和回波强度的对应关系[14],如表1所示。
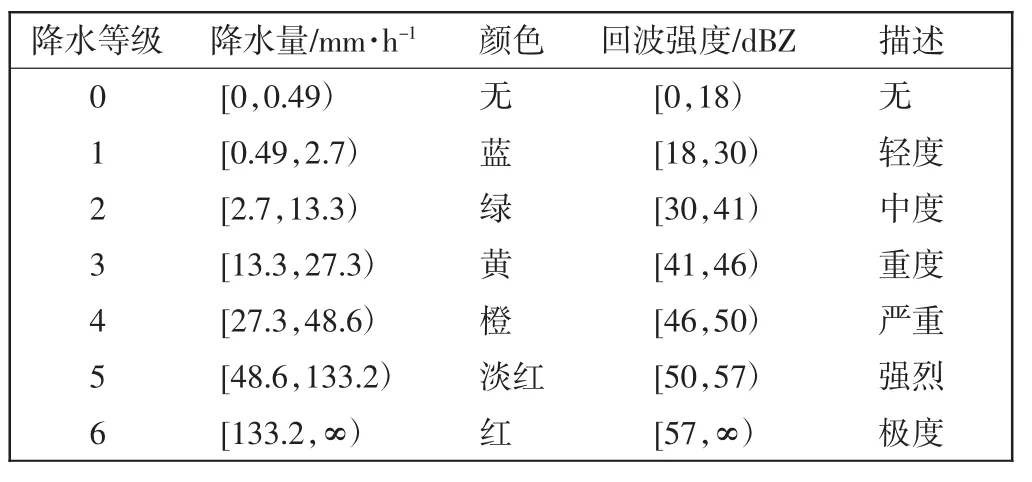
表1 降水等级、颜色和回波强度关系Tab.1 Precipitation grade,colors and echo intensity
当天气条件处于降水等级1时,即进场航段受蓝色降水天气影响时,管制员会增大航空器的水平间隔以保证航空器安全飞行。根据雷达管制最低水平间隔标准,进近管制不得小于6 km[15],但同时考虑终端空域容量限制,实际管制间隔应小于进近管制间隔标准的2倍。设雷达管制最低水平间隔标准为d,管制间隔系数为α,受蓝色降水天气影响后的管制间隔为d′,则d′=αd。显然管制间隔越大,航班的延误时间越长。
当天气条件处于降水等级2及以上时,即进场航段受绿色、黄色、橙色、淡红、红色降水天气影响,航空器将进行改航、备降或返航。对于航空器改航情况,设受降水影响的进场航段长度为L,改航距离系数为β,改航之后的路径长度为L′,则L′=βL,β>1。由于改航路径是由飞行员根据机载雷达设备所提供的天气信息进行机动飞行,所以改航路径的距离对航班延误时间有直接影响,改航距离越长,航班的延误时间越长。
2 三维WITI计算模型
WITI指数是指受降水天气影响的航空器数量,航空器数量越大,天气影响程度越严重。本文将WITI的概念应用于终端空域短期天气条件变化的背景下,并结合多普勒气象雷达提供的PPI和RHI图像,以及管制部门提供的雷达轨迹数据,提出三维WITI指数的计算模型,其计算公式如下
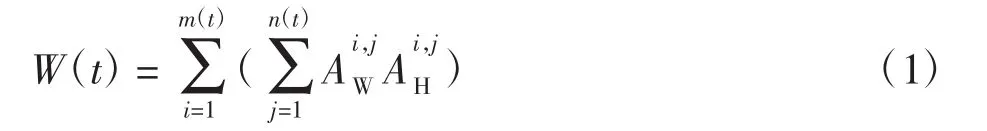

其中:Pi和hi分别为第i架航空器在终端空域的平面坐标和高度坐标;W(t)为t时段的WITI指数;m(t)为t时段终端空域内航空器数量;n(t)为t时段终端空域降水云团数量;为航空器ai的平面位置判定参数;为航空器ai的高度位置判定参数;Wj为第j个降水云团的二维平面轮廓内的点集合;为第j个降水云团的云底高;为第j个降水云团的云顶高。
根据多普勒雷达提供的平面位置显示PPI图像,可利用Matlab图像处理的颜色识别和轮廓提取方法获得不同等级的降水云团轮廓线,结合航空器的飞行轨迹,判断航空器是否位于降水云团所影响的范围内,若是;反之
航空器ai所在的高度层根据t时刻航空器所在的终端区进场航段确定,根据机场标准仪表进场程序,并结合实际管制员的行为习惯,可得到不同进场航段所处的不同高度层。降水云团的高度数据包括云底高、云顶高,根据多普勒气象雷达提供的距离高度显示RHI图像获取云高数据。若航空器的高度位于云底高与云顶高之间,则;反之
根据雷达回波图像反映出的不同降水等级,将会有不同的管制间隔和改航路径。通过Matlab识别出雷达回波图像中蓝色区域和绿色区域的边界,并匹配交通流数据后,利用上述WITI指数计算方法可得到不同降水等级条件下受影响的航空器数量。
综上,WITI指数是由终端空域内的天气条件和交通流状况决定的,而终端空域内的天气条件和交通流状况随时间变化而变化,呈现动态性,故WITI指数在不同时间段的数值将会不同。
3 终端空域短期延误预测模型
根据降水等级分为两种情景模式:
情景1 天气条件为降水等级1,管制间隔系数为α。在情景1中引入管制间隔系数α,其意义为该天气条件下2架航空器的管制间隔标准与正常天气条件下管制间隔标准之间的比值,α取值在1~2之间。
情景2 天气条件为降水等级2及以上,改航距离系数为β。在情景2条件下引入改航距离系数β,其意义在于航空器改航路径的距离与原进场航段距离的比值,β>1。
文献[10]对航路阶段的延误时间与天气影响交通指数WITI建立了线性回归模型,其研究结果表明延误时间与WITI呈现明显的线性关系;而针对终端空域的复杂天气条件和交通流状况,两者有可能线性相关关系,更有可能是非线性关系。当终端空域达到饱和容量时,其管制负荷也急剧增大,产生的航班延误急剧增大,故对延误时间与WITI建立指数回归模型。
假设延误时间与WITI指数之间的关系为

其中:D为延误时间;W为WITI指数;a、b为相关系数。
4 算例仿真
本文以上海终端空域2016年04月02日12:00—20:30的降水过程为例,选取终端区气象雷达回波图像以及交通流数据,利用Visual Basic对上海终端区的交通流数据进行仿真,采用Matlab的图像处理工具对气象雷达回波图像进行颜色识别与轮廓提取,得到天气与交通流的匹配数据,计算三维WITI指数,并得到不同情景下的延误预测模型,如图1所示。
4.1 不同降水等级的WITI指数
第1步 不同降水等级下受影响的进场航段。
情景1 针对图1(a)中雷达回波PPI图提取蓝色区域轮廓,与上海终端空域结构匹配,得到受影响的进场航段为AND-DADAT-BELOP-XSY航段和AND-IDNIK-IGLIT-XSY航段,如图1(c)所示。
情景2 针对图1(a)中雷达回波PPI图提取绿色区域轮廓,与上海终端空域结构匹配,得到受影响的进场航段为AND-IDNIK-IGLIT-XSY航段,如图1(d)所示。
由于AND-IDNIK-IGLIT-XSY航段同时受到蓝色区域和绿色区域覆盖,故以AND-IDNIK-IGLITXSY进场航段为例对不同天气情景条件下的延误状况进行分析。
为了精确得到影响AND-IDNIK-IGLIT-XSY航段降水云团的高度范围,对图1(b)雷达回波RHI图提取蓝色轮廓和绿色轮廓得到图1(e)和图1(f)。由于RHI像素为600×600,而RHI图像中坐标轴原点的像素为(41,481),高度20.0 km的像素点为(41,118),故RHI图像中高度范围内每个像素代表55 m。提取蓝色轮廓图中最高点的像素为(92,337),云顶高为(481-337)×55=7 920 m;提取绿色轮廓图中最高点的像素为(65,395),其云顶高为(481-395)×55=4 730 m。

图1 雷达回波PPI和RHI图Fig.1 Radar echo PPI and RHI
由以上分析可知,AND-IDNIK-IGLIT-XSY进场航段共同受蓝色区域和绿色区域影响,且识别的蓝色区域云顶高为7920m,绿色区域云顶高为4730m。而庵东进场高度为5 100 m,DADAT报告点高度为3 500 m。
第2步 不同天气情景条件下计算WITI指数。
将图2中7架航空器自左向右分别编号i=1,…,7,2个降水云团分别编号j=1,2。第1个降水云团的云底高,云顶高;第2个降水云团的云底高,云顶高。对执行航班CCA198的第1架航空器a1,其平面位置位于绿色轮廓内,故;航空器a1所在高度为4 620 m,在云高与之间,故。对其余6架航空器分别计算,结果如表2所示。

图2 PPI绿色轮廓与交通流示意图Fig.2 PPI green contour and air traffic flow
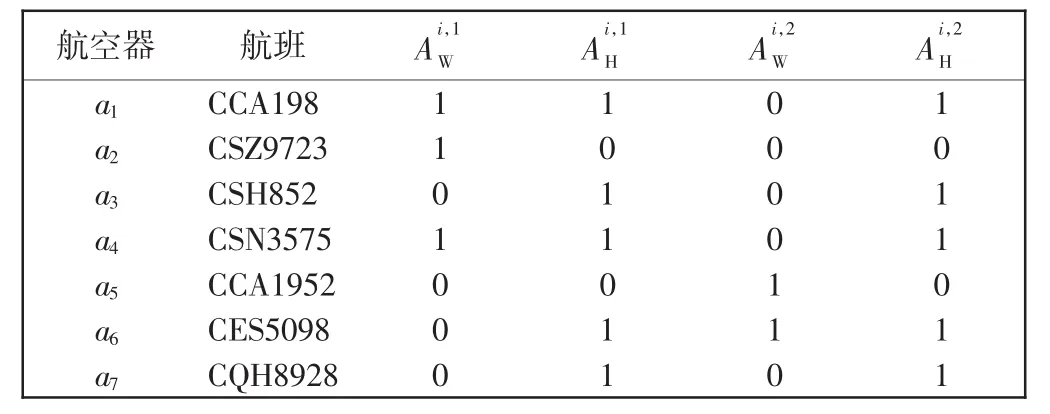
表2 航空器1~7的位置参数和高度参数Tab.2 Position and altitude parameters of Aircraft No.1~No.7
该时刻终端空域内WITI指数W(t)计算如下

该空域内有7架航空器,而WITI指数的计算结果为3,表示该空域内只有a1、a4、a6这3架航空器受天气影响;a2、a5为飞越航空器,飞行高度大于降水云团云顶高,故不受天气影响;航空器a3、a7在降水云团轮廓外,故不受天气影响。
由于12:00—20:30的降水过程中降水云团的位置高度、降水强度均在实时动态变化,AND-IDNIKIGLIT-XSY进场航段受降水天气影响的范围和程度也在实时变化,故选取每0.5 h的雷达回波图像与交通流数据进行匹配,仿真统计WITI指数的周期为0.5 h,一共得到12 h的WITI变化趋势,如图3所示。其中B-WITI表示情景1天气条件影响下的WITI指数,GWITI表示情景2天气条件影响下的WITI指数。

图3 AND-IDNIK-IGLIT-XSY航段WITI指数Fig.3WITI index of AND-IDNIK-IGLIT-XSY
4.2 不同情景的延误预测模型
对情景1条件下设定不同的管制间隔系数α,情景2条件下设定不同的改航距离系数β,仿真得到的延误时间分析如下:
情景1 在原有的前后机间隔为60 s的基础上,分别设定管制间隔系数α=1.2、1.5、1.8。为了分析延误时间与B-WITI指数的变化趋势,将延误时间缩小至原来的1/100,使两者取得相同的数量级,如图4所示。

图4 α=1.2、1.5、1.8时延误时间Fig.4 Delays when α=1.2,1.5,1.8
从图4可看出,在12:00—20:30受降水条件影响的过程中,WITI指数和延误时间的变化趋势均相同,表明管制间隔影响下的延误时间与WITI正相关,且管制间隔越大,延误时间越大。
对延误时间和WITI建立指数回归模型,与文献[10]的线性回归模型相比,两者的拟合曲线图如图5所示,模型相关系数、拟合优度和估计标准误差,如表3所示,对比分析得到指数模型的拟合优度相对更优,且指数模型的估计标准误差SEE均趋于0。在管制间隔系数α=1.2、1.5、1.8的条件下,得到3个短期延误预测模型,即
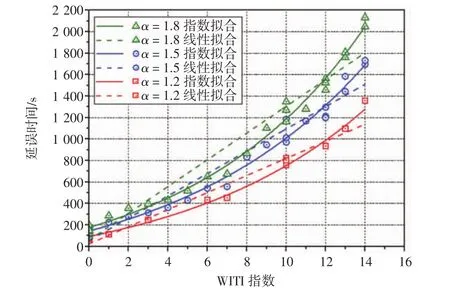
图5 α=1.2、1.5、1.8时延误时间与WITI指数的关系Fig.5 Relationship between delay and WITI when α=1.2,1.5,1.8

表3 α=1.2、1.5、1.8时模型汇总Tab.3 Model summary when α=1.2,1.5,1.8
情景2 原AND-IDNIK-IGLIT-XSY进场航段距离为105.43 km,由于受降水天气影响现规划3条改航路径,距离分别为126.62km、137.10km和159.25km,与原有进场航段距离相比分别是其1.2、1.3、1.5倍。故将仿真程序中改航距离系数β分别设定为1.2、1.3、1.5。为了分析延误时间与G-WITI指数的变化趋势,将延误时间缩小至原来的1/300,使两者取得相同的数量级,如图6所示。
从图6可看出,在12:00—20:30受降水条件影响的过程中,WITI指数和延误时间的变化趋势均相同,表明改航影响下的延误时间与WITI正相关,且改航距离越大,延误时间越大。
对延误时间和WITI建立指数回归模型,与线性回归模型相比,指数模型的拟合优度相对更优,如图7所示,且指数模型的估计标准误差SEE均趋于0,如表4所示。在改航距离系数β=1.2、1.3、1.5的条件下,得到3个短期延误预测模型,即

综上分析,对情景1和情景2条件下的WITI指数进行比较,情景1条件下的WITI指数比情景2的大,表明雷达回波PPI图像中蓝色区域的影响范围比绿色区域的大,故受降水等级1影响的航空器数量大;对情景1和情景2条件下的延误时间进行比较,改航情况下的延误时间比增大管制间隔所引起的延误时间更大,相应的延误成本也更大。
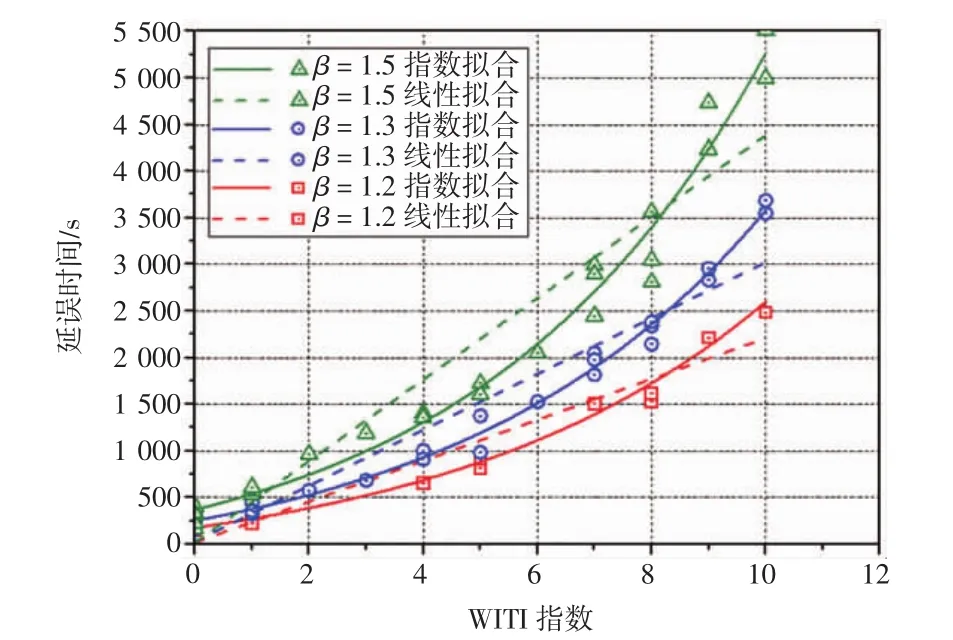
图7 β=1.2、1.3、1.5时延误时间与WITI的关系Fig.7 Relationship between delay and WITI when β=1.2,1.5,1.8
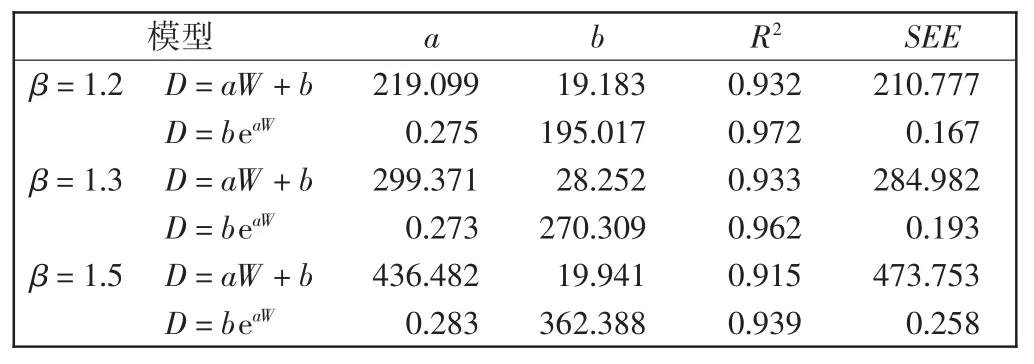
表4 β=1.2、1.3、1.5时模型汇总Tab.4 Model summary when β=1.2,1.3,1.5
5 结语
本文提出在不同降水等级条件下的三维终端空域WITI指数的计算方法,并利用线性回归方法建立短期延误预测模型,通过案例仿真验证了延误预测模型的正确性和有效性。具体包括:①提出三维WITI指数计算模型,即考虑了降水云团云顶高数据,与航空器高度进行比较,确定航空器是否受到影响,更加精确统计了受降水天气影响的航空器数量;②考虑在不同降水等级条件下不同管制措施对延误时间的影响,即通过指数回归分析得到短期延误预测模型,相比线性回归模型预测的延误时间更加符合实际,分析得到延误时间与天气条件和管制员管制调配策略有关。
[1]CALLAHAM M B,DEARMON J S,COOPER A M,et al.Assessing NAS Performance:Normalizing for the Effects of Weather[C]//4th USA/Europe Air Traffic Management R&D Symposium,Santa Fe,NM,2001.
[2]CHATTERJIG,SRIDHARB.NationalAirspaceSystemDelayEstimation Using Weather Weighted Traffic Counts[C]//AIAA Guidance Navigation and Control Conference,San Francisco,2005:1-17.
[3]SRIDHAR B,SWEI S.Classification and Computation of Aggregate DelayUsingCenter-BasedWeatherImpactedTraffic Index[C]//7th AIAA AviationTechnology,IntegrationandOperations Conference(ATIO),Belfast,Northern Ireland,2007.
[4]KLEIN A,JEHLEN R,LIANG D.Weather Index With Queuing Component For National Airspace System Performance Assessment[C]//7th USA/Europe ATM R&D Seminar,Barcelona,Spain,2007.
[5]HANSEN M,XIONG J.Weather Normalization for Evaluating National Airspace System(NAS)Performance[C]//7th USA/Europe ATM R&D Seminar,Barcelona,Spain,2007.
[6]KLEIN A,KAVOUSSI S,HICKMAN D,et al.Predicting Weather Impact on Air Traffic[C]//ICNS Conference,Herndon,VA,2007.
[7]KLINGLE WILSON D,EVANS J.Description of the Corridor Integrated Weather System(CIWS)Weather Products,Project Report ATC-317[R].Lexington:MIT Lincoln Laboratory,2005.
[8]SRIDHAR B,CHEN N.Short term national airspace system delay prediction using weatherimpactedtrafficindex[J].Journalof Guidance Control and Dynamics,2009,32(2):657-662.
[9]CHEN N,SRIDHAR B.Estimation of Air Traffic Delay Using Three Dimensional Weather Information[C]//The 26th Congress of International CounciloftheAeronauticalSciences,Anchorage,Alaska,2008:8916.
[10]DIANA M,HAMSA B.Dynamic Reconfiguration of Terminal Airspace During Convective Weather[C]//49th IEEE Conference on Decision and Control,Atlanta,GA,2010:4875-4881.
[11]SCOT C,RICH D.Convective Weather Impact Forecasting in the Terminal Area[C]//14th AIAA Aviation Technology Integration and Operations Conference,Atlanta,GA,2014:2715.
[12]ISON D,WEILAND L,MCANDREW I,et al.Identification of air traffic management principles influential in the development of an airport arrival delay prediction model[J].Journal of Aviation/Aerospace Education&Research,2015,24(2):39-53.
[13]黄仪方.航空气象[M].2版.成都:西南交通大学出版社,2011.
[14]LINDHOLM T,SHARMAN R,KROZEL J,et al.Translating Weather into Traffic Flow Management Impacts for NextGen[C]//14th Conference on Aviation Range and Aerospace Meteorology American Meteorological Society,Atlanta,GA,2010
[15]董襄宁.空中交通管理基础[M].北京:科学出版社,2011.
(责任编辑:孟 欣)
Short-term terminal airspace delay prediction based on weather impacted traffic index
ZHANG Ming1,ZHANG Ming1*,LIU Kai1,ZHAO Min2
(1.College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China; 2.Jiangsu Province Safety Oversight Bureau,CAAC,Nanjing 210022,China)
Aiming at the flight delay in terminal airspace caused by the changes of short-term weather conditions,radar echo PPI(plane-position indication)and RHI(range-height indication)are firstly used to classify the precipitation grades,then the contour of different grades of convective clouds is extracted by image recognition method.Secondly,the corresponding time of traffic flow information is matched to the convective clouds,and the calculation method of 3D WITI(weather impacted traffic index)based on different levels of precipitation is put forward.Finally,according to air traffic control rules,a short-term delay prediction model is proposed through exponential regression analysis between WITI and delay time under different control intervals or rerouting path distance.Simulation results show that under the condition of control interval adjustment and rerouting,compared with the linear regression model,the fit goodness of exponential regression model increases 1.6%~4.3%,and the standard error of estimate is closed to 0,indicating that the exponential regression delay prediction model can better reflect the actual delay situation of terminal airspace under the influence of precipitation.
terminal airspace;precipitation grades;air traffic flow;WITI;delay prediction
V355.1
A
1674-5590(2017)02-0005-06
2016-06-14;
2016-07-13
国家自然科学基金项目(U1233101,71271113);中央高校基本科研业务费专项(NS2016062)
张明(1991—),男,山东临沂人,硕士研究生,研究方向为空中交通规划与管理.
张明*(1975—),男,江苏南京人,副教授,博士,研究方向为空中交通管理.

