一种改进的星载GPS周跳探测与修复方法
陈逸伦, 郝金明,于合理,田英国,邓科
(1.信息工程大学 导航与空天目标工程学院,河南 郑州 450001,2.北斗导航应用技术河南省协同创新中心,河南 郑州 450001)
一种改进的星载GPS周跳探测与修复方法
陈逸伦1,2, 郝金明1,2,于合理1,2,田英国1,2,邓科1,2
(1.信息工程大学 导航与空天目标工程学院,河南 郑州 450001,2.北斗导航应用技术河南省协同创新中心,河南 郑州 450001)
周跳探测与修复是星载GPS数据预处理的重要内容。首先使用SWARM卫星实测数据对TurboEdit算法的有效性进行了分析,针对算法在观测噪声较大情况下无法有效探测小周跳的问题,提出了一种改进算法。该算法利用载波相位观测值对伪距组合观测值进行平滑,降低了观测噪声对宽巷模糊度的影响,提高了周跳探测能力。实验结果表明,改进算法能够有效提高小周跳的探测能力。
星载GPS数据预处理;小周跳探测与修复;TurboEdit;载波相位平滑
0 引 言
当前,低轨卫星在地球重力场测量、气象研究、遥感监测等领域发挥着日益重要的作用。在应用各类低轨卫星展开科学研究时,面临的第一个问题就是确定和预报低轨卫星轨道。全球定位系统(GPS)因为其可靠性强、可持续观测、精度高等优点成为了低轨卫星定轨的常用手段。许多类型的低轨卫星对定轨精度有很高要求.[1],如重力测量卫星CHAMP、GRACE,磁力测量卫星SWARM,对轨道精度的要求都在cm级。为了获得较高的定轨精度,必须对星载GPS数据进行严格预处理。如何有效探测和修复载波相位观测值上的周跳,是其中一个重要内容。
常用的周跳探测方法包括多项式拟合法、高次差法、卡尔曼滤波法、电离层残差法、TurboEdit等[2-3]。其中TurboEdit法广泛运用于星载GPS数据的周跳探测与修复。该方法综合运用M-W组合和电离层组合来唯一确定两个频率上周跳的大小,在计算过程中消去了卫星到接收机的几何距离、电离层误差、卫星钟差、接收机钟差等多种误差[4],可以较好的适用于星载数据预处理。但在伪距观测值观测噪声较大的情况下,TurboEdit法无法有效探测小周跳。针对这一问题,本文提出了一种改进算法。该方法为降低伪距噪声影响,使用载波相位观测量对宽巷组合观测值进行平滑,进而提高对小周跳探测能力。
1 TurboEdit法基本原理与分析
TurboEdit法首先由Blewitt提出,该方法综合使用了M-W组合和电离层组合来探测和修复周跳,同时也可以剔除粗差。
1.1 M-W组合
使用双频观测值时,宽巷组合可以表示为[5]
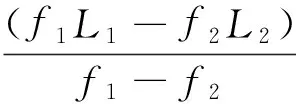
(1)
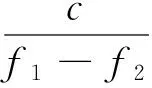
为了计算宽巷组合的整周模糊度,构造下列伪距观测量的线性组合:
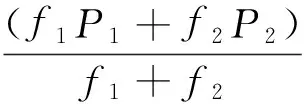
(2)
式中:P1、P2分别为L1、L2频率上的P码伪距观测值。由式(1)、式(2)可以计算宽巷组合的整周模糊度:
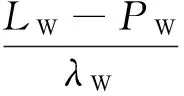
(3)
上述公式即为M-W公式。式中:NW为宽巷的整周模糊度;N1、N2分别为L1、L2上的整周模糊度。当没有周跳发生时,N1、N2保持为一常数,若不考虑噪声和误差的影响,每一历元NW应是一固定值。若在第k历元时L1、L2上发生了大小为(ΔN1,ΔN2)的周跳,由式(3)可知,ΔNW(k)=NW(k)-NW(k-1)=ΔN1-ΔN2.为了使用M-W公式探测和修复周跳,TurboEdit法使用了如下递推算法:
(4)
σ2(i)=σ2(i-1)+
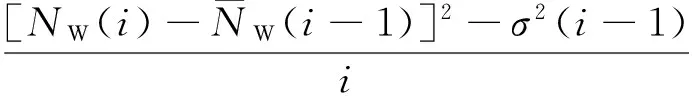
(5)
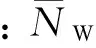
(6)
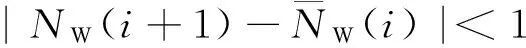
(7)
1.2 电离层组合
电离层组合可以表示为
Li=L1-L2
=I+λ1NW-λiN2,
(8)式中:λi=λ2-λ1为电离层残差组合的波长;I为电离层延迟参数。在探测并计算出宽巷周跳NW后,为了唯一确定两个频率上周跳的大小,还需要求出电离层组合周跳ΔNi=λ1ΔNW-λiΔN2的大小。
由ΔNW(k)=NW(k)-NW(k-1)=ΔN1-ΔN2,可知如果在两个频率上发生大小相同的周跳ΔN1=ΔN2,则ΔNW(k)=0,此时M-W组合无法探测周跳的发生。为了应对这种情况,TurboEdit给出了使用电离层组合探测周跳的方法。构造伪距观测值线性组合:
Pi=P2-P1=I.
(9)
为了减轻伪距观测噪声对探测的影响,对Pi进行多项式拟合,拟合结果为Qi.当满足下列条件时,则判定k历元发生了周跳:
[Li(k)-Qi(k)]-[Li(k-1)-Qi(k-1)]>6λi,
(10)
[Li(k+1)-Qi(k+1)]-[Li(k)-Qi(k)]<λi.
(11)
当M-W组合或电离层组合探测到k历元发生周跳时,采用k历元之前一系列历元的数据对Li进行拟合,再将拟合结果外推到第k历元。将实际观测结果和外推结果做差即可得到电离层组合的周跳大小ΔNi.联立方程组:
(12)
即可求得k历元两个频率上周跳的大小的估值。
1.3 算例分析
下面根据实际算例来对传统TurboEdit方法有效性进行分析。数据采用来自SWARM卫星星载接收机的GPS观测数据,观测时间为2016年2月1日,采样间隔1s. 分别在17号卫星第1000历元加入(1, 0)周周跳,30号卫星第2000历元加入(0, 2)周周跳。采用传统TurboEdit对加入周跳的观测数据进行探测,探测结果如图1、图2所示。
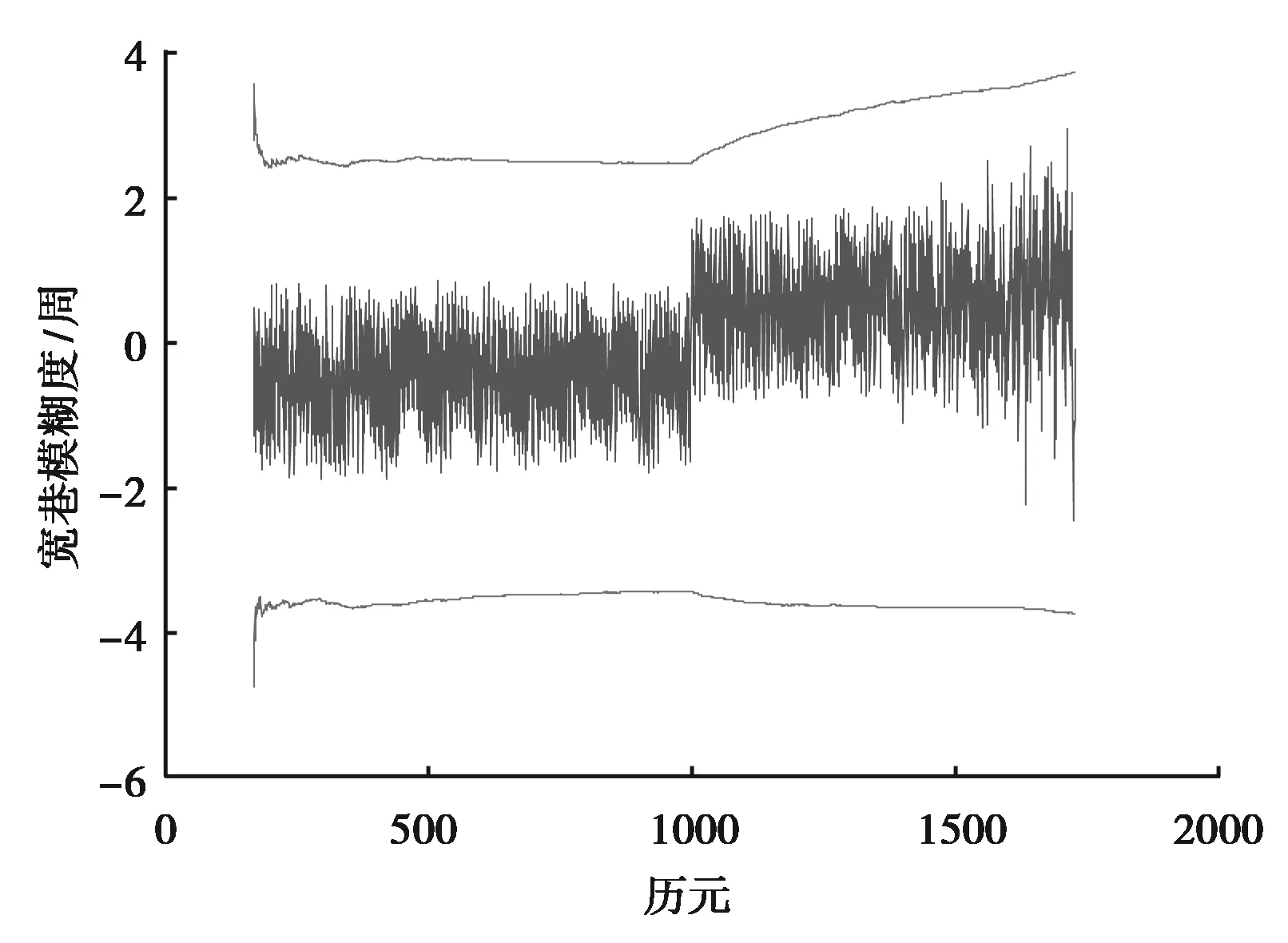
图1 TurboEdit探测1周周跳结果
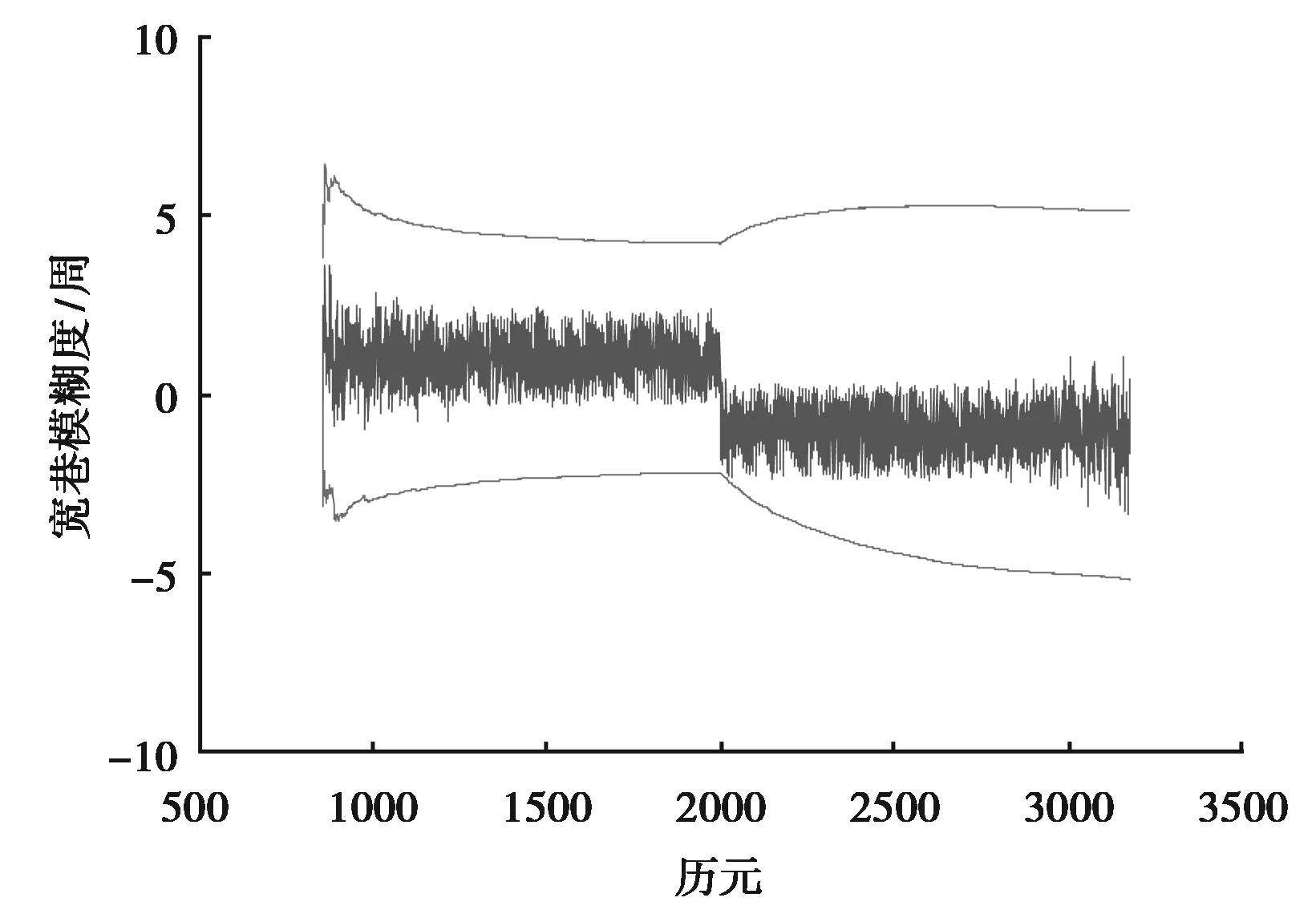
图2 TurboEdit探测2周周跳结果
图1、图2所示的中心曲线即为每历元NW的值,上下两条曲线为由式(6)计算出的判断边界。当某一历元NW(k)落在判断边界以外时,TurboEdit算法才有可能判定周跳的发生。从图中可以看出,当分别加入1周和2周周跳时,NW(k)的计算值依然落在判断边界以内,M-W组合无法有效的探测周跳的发生。此时,算法判定ΔNW=0,即使电离层组合成功探测到周跳的存在,也会导致周跳的大小计算错误。
产生这种情况的主要原因是组合观测值的噪声过大,特别是在计算NW(k)时使用了伪距观测量的线性组合PW,导致NW计算结果中误差较大,根据式(6)的判断标准,影响了算法的探测能力。还可以看出,在M-W组合探测周跳失败的情况下,均值和方差的计算不会重置,对后续式(6)、式(7)判断边界的计算也产生了影响,进一步减弱了算法的探测能力。
为了减弱伪距观测量观测噪声对周跳探测的不利影响,下面将载波相位平滑算法引入TureboEdit。
2 TurboEdit改进算法
和伪距观测值相比,载波相位观测值有更高的观测精度,更小的观测噪声,并且受到多路径效应的影响较小[6]。在这里,使用LW对PW进行平滑处理,以降低其观测噪声,平滑后的伪距观测值由下式得到:
(13)
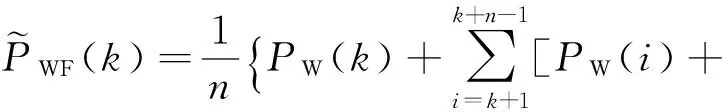
(14)
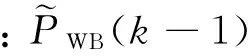

(15)
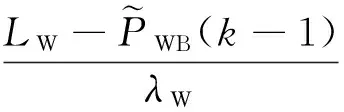
(16)
为了探测周跳的发生,构造观测量:
ΔNW(k)=NW(k)-NW(k-1) .
(17)
为了对比分析改进算法的周跳探测能力,采用和图1、图2相同的观测数据计算每历元ΔNW(k),结果如图3所示。这里设定m=n=25.为了更好地观察ΔNW(k)的特性,每组图都去掉了人工周跳,图3数据和图1、图2完全一致,在相同的位置加入了人工周跳。为了便于观察,加入周跳的历元用虚线进行了标识。
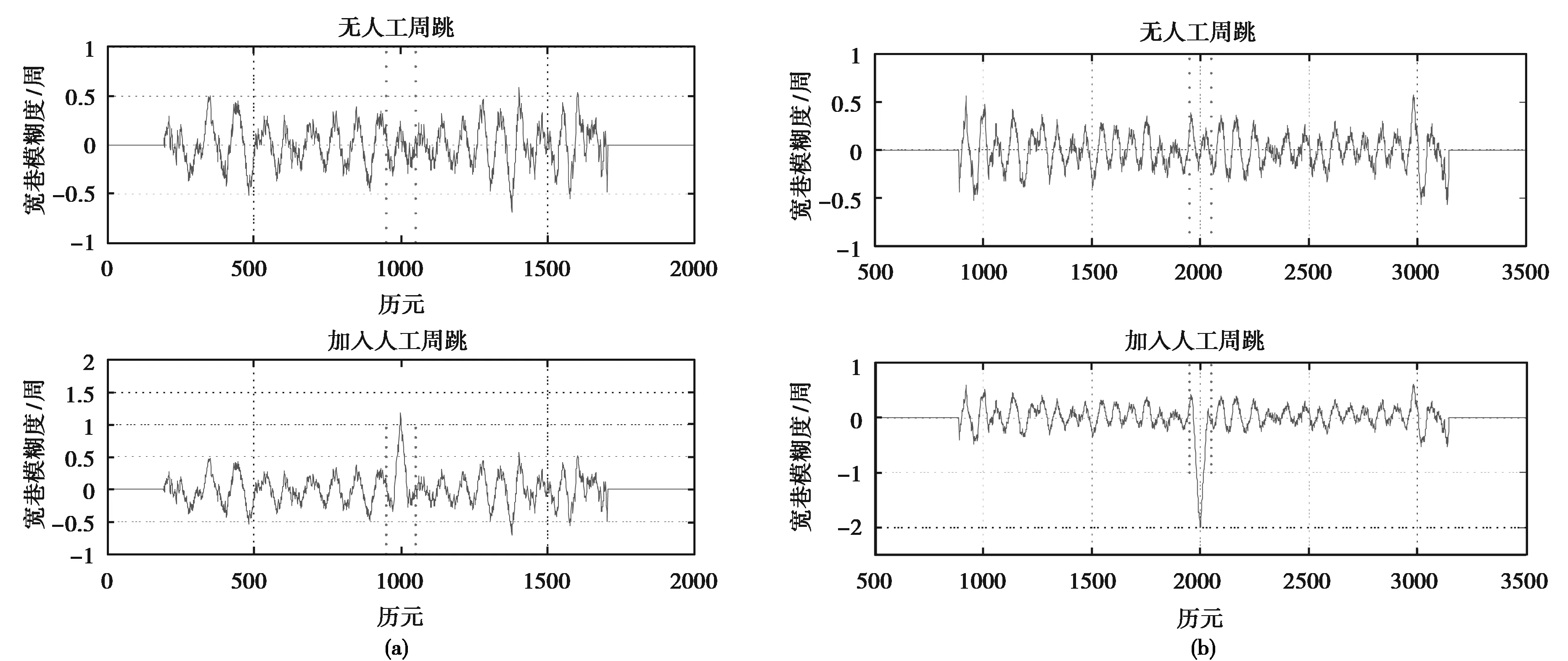
图3 改进算法探测小周跳结果 (a) 1周周跳;(b) 2周周跳
从图3可以看出,当没有加入人工周跳时,ΔNW(k)在一定范围内波动,均值在误差允许范围内近似为0.ΔNW(k)上下波动的幅度和观测值的噪声水平以及平滑所用到历元数有关,在选取合适的m、n值情况下,ΔNW(k)大体分布在(-0.5, 0.5)周。当加入人工周跳后,在加入周跳的历元ΔNW(k)发生了明显的跳变。由ΔNW(k)=NW(k)-NW(k-1)=ΔN1-ΔN2,可知跳变的值实际上反映的就是宽巷模糊度周跳的大小。将跳变值四舍五入,即可得到宽巷模糊度周跳的真值。确定了宽巷组合周跳ΔNW(k)后,即可结合电离层组合解算出两个频率上周跳的大小,并对其进行修复。由图1、图2、图3对比可以看出,改进算法对小周跳有较好的探测能力。其中平滑所用到m、n值的可以根据NW(k)精度来决定,一般可以设定为NW(k)中误差的50倍[7]。需要注意的是,该方法同时采用了后向平滑和前向平滑,适用于事后数据处理,当待探测历元在之后n个历元内没有其他周跳的发生时,探测效果最佳。
3 实验分析
下面采用SWARM卫星GPS接收机观测数据对算法有效性进行进一步验证,观测时间为2016年2月2日,采样间隔为1s.在多颗卫星的若干历元加入了人工周跳的组合,分别使用传统TurboEdit法和载波相位平滑改进算法对周跳进行探测,一部分加入周跳的卫星与历元在图4中进行了标记,探测结果如表1所示。
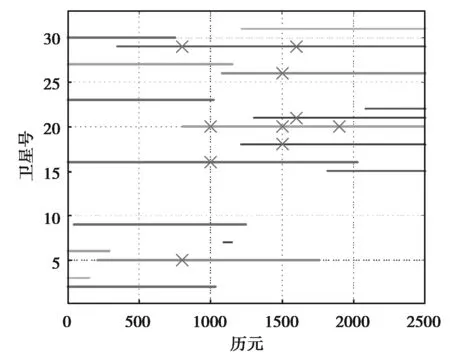
图4 加入人工周跳的位置
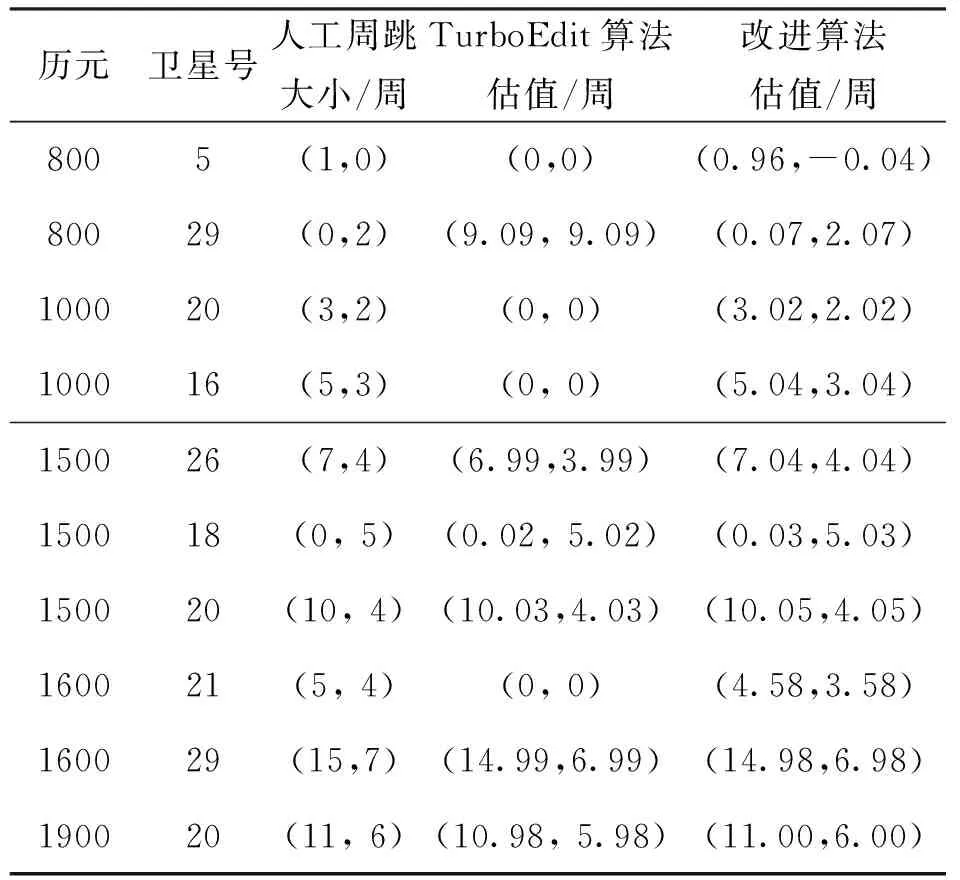
表1 传统TurboEdit与改进算法部分探测结果对比
从表1可以看出:
1) 传统TurboEdit法对大周跳具有较好的探测与修复效果,但是对(1, 0)、(0, 2)、(3, 2)、(5, 3)、(5, 4)这种引发宽巷模糊度小周跳的周跳组合探测效果不佳,很难探测出周跳的发生,尤其是在29星800历元,在电离层组合探测周跳成功,M-W组合探测失败的情况下,甚至得到了错误的周跳估值。这主要是因为SWARM星载数据伪距观测噪声过大导致传统算法失效。
2) 改进算法与传统TurboEdit法对大周跳的探测修复能力基本相当,但能显著提高对宽巷模糊度小周跳的探测能力,基本可以探测出各种类型的小周跳组合。结合电离层组合法,可以有效的估计两个频率上周跳的大小。在宽巷周跳正确固定的情况下,估计的精度主要受电离层残差的影响,经过四舍五入后,可以正确的得到人工周跳的真值。需要注意的是,少数情况下该方法对周跳的估值会出现一定的偏差,例如表1中21星第1600历元。出现这种情况的原因是平滑算法采用的平滑历元数量不足,没有充分消除伪距噪声的影响,平滑历元数在实际探测中应根据需要进行调整。
4 结束语
针对TurboEdit法在观测噪声,特别是伪距观测噪声较大条件下无法有效检测小周跳的问题,本文提出了一种改进算法。该算法使用双向载波相位平滑法结合电离层残差法,原理简单,计算量小,可以唯一确定和修复双频周跳。经SWARM卫星星载数据验证,该方法有效减小了观测噪声对周跳探测的不利影响,有效提高了对小周跳探测能力,适用于事后周跳探测。如何动态的确定平滑历元数,兼顾算法的探测精度和可靠性,是需要继续研究的问题。
[1] 冯来平, 阮仁桂, 吴显兵, 等. 联合低轨卫星和地面监测站数据确定导航卫星轨道 [J]. 大地测量与地球动力学, 2016, 36(10): 864-869.
[2] KARAIM M, KARAMAT T B, NOURELDIN A,etal. GPS cycle slip detection and correction at measurement level [J]. British Journal of Applied Science & Technology, 2014, 4(29): 4239-4251.
[3] 李征航. GPS测量与数据处理 [M]. 武汉:武汉大学出版社, 2010: 143-149.
[4] 王敬, 赵军祥. Blewitt周跳探测方法的改进 [J]. 飞行器测控学报, 2011, 30(2): 80-83.
[5] GEOFFREY B. An automatic editing algorithm for GPS data [J]. Geophysical Research Letters, 1990, 17(3): 199-202.
[6] 焦海松, 杨海强, 马国元, 等. 载波相位平滑伪距单点定位精度分析 [J]. 全球定位系统, 2009, 34(4): 41-46.
[7] CAI C, LIU Z, XIA P,etal. Cycle slip detection and repair for undifferenced GPS observations under high ionospheric activity[J]. GPS Solutions, 2013, 17(2): 247-260.
A Improved Cycle Slip Detection and Repair Method for On-board GPS Data
CHEN Yilun1,2, HAO Jinming1,2, YU Heli1,2, TIAN Yingguo1,2,DENG Ke1,2
(1.InstituteofNavigationandAerospaceTarget,UniversityofInformationEngineering,Zhengzhou, 450001China; 2.BeidouNavigationTechnologyCollaborativeInnovationCenterofHenan,Zhengzhou450001,China)
Cycle slip detection and repair is an essential part of on-board Global Positioning System (GPS) data pre-processing. In this contribution, the effectiveness of TurboEdit algorithm is firstly analyzed using on-board GPS data observed by Swarm satellite. After that, an improved method is proposed, considering that TurboEdit algorithm can not detect small cycle slips when the observation noise is large. This new method uses carrier phase to smooth combined pseudorange observations and therefore reduces the impact observation noise laid on wide lane ambiguity and improves the capability of cycle slip detection. The method is tested and results show that it can effectively detect and repair small cycle slip.
On-board GPS data pre-processing; small cycle slip detection; TurboEdit; carrier phase smoothing
10.13442/j.gnss.1008-9268.2017.02.007
2016-10-27
P228.4
A
1008-9268(2017)02-0032-05
陈逸伦 (1992-),男,硕士生,研究方向为星载GNSS数据预处理。
郝金明 (1962-),男,教授,主要从事卫星导航与精密定位等方面的教学与研究。
于合理 (1989-),男,博士生,主要从事GNSS时频传递及时差监测算法研究。
田英国 (1987-),男,博士生,主要从事低轨卫星精密定轨方面的研究。
邓科 (1991-),男,硕士生,主要从事GNSS接收机相位中心误差建模方面的研究。
联系人: 陈逸伦 E-mail:1024169662@qq.com

