频率选择性衰落信道下空时分组码盲识别技术综述∗

频率选择性衰落信道下空时分组码盲识别技术综述∗

林洪文1于柯远1钟兆根1刘昭2

（1.海军航空工程学院电子信息工程系烟台264001）（2.海军荣成导航台荣成264300）

空时分组码盲识别技术是通信信号盲识别技术中一个新的重要方向，在频率选择性衰落信道条件下对空时分组码盲识别进行研究具有十分重要的现实意义。论文首先介绍了频率选择信道下对空时分组码盲识别研究的意义，分别在单载波和多载波条件下对空时分组码盲识别类型识别方法进行分类，并概述了每种算法的关键识别思想，并对其进行了对比总结，最后展望了在频率选择性衰落信道下的空时分组码识别算法的难点和未来趋势。

空时分组码；频率选择性衰落信道；单载波传输；正交频分复用

Class NumberTN911.7

1 引言

随着MIMO通信技术的发展，非合作方对通信信号的侦察和参数估计也变得愈发困难，对非合作方提出了更高的要求。MIMO系统以其充分利用空间资源的优势，成为下一代无线通信系统中的关键技术。空时分组码（Space-Time Block Code，ST⁃BC）作为一种基于MIMO系统的编码方案，其盲识别［1～3］问题受到越来越多的关注。

随着空时分组码的应用和通信对抗技术的发展，它成为移动通信领域中重要组成部分，是通信信号盲识别技术中一个新的重要方向，特别是在军事领域。然而大部分研究者对于空时分组码盲识别的研究都假设信道满足平坦的慢衰落条件［4～7］，且各信道的衰落互相独立，然而在实际的通信环境中，由于信道传播条件较为恶劣，使无线信道的特性随时间变化，造成信号的衰落，严重影响通信质量，所以为了探讨空时分组码技术在无线信道中的实用性，有必要对空时分组码在频率选择性衰落信道中的盲识别进行研究。

目前还没有对在频率选择性衰落信道下针对空时分组码盲识别的综述类文献，本文针对这一问题，分别在单载波和多载波两种条件下进行讨论，并介绍了具有代表性的识别算法［8～17］，并对其识别效果进行了比较讨论。

2 空时分组码

空时分组码的类型很多，常用的空时分组码有两种，大多数识别算法主要采取了SM-STBC码和AL-STBC码。

SM-STBC：发射天线数为nt=j，码矩阵长度L=1

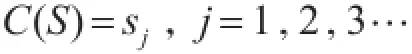
AL-STBC：发射天线数为nt=2，码矩阵长度L=2

3 频率选择性衰落信道

在实际的无线通信系统中，信道传播条件比较恶劣，发射信号经过散射、反射等多条路径到达接收端，同时产生多径衰落，严重影响了系统的性能。

从时域上看，多径衰落的码元间隔Ts大于最大多径时延τmax，就会产生码间干扰（ISI），此时的信道呈现频率选择性信道。

假设信道满足以下条件［5］：1）各信道之间的衰落相互独立；2）各信道之间具有时域对称性；3）所有多径能被准确分离。

信道模型：在频率选择性衰落信道中，具有相同多径时延的信号在不同频率分量上经历不同的衰落，从时域上来看，接收信号经历多个可分辨径的衰落，具有严重的码间干扰（ISI）。接收信号可以表示为发送信号和多径信道的卷积，信道部分由多径瑞利（Rayleigh）信道和高斯白噪声构成。

接收信号经历频率选择性衰落信道后，第k个接收符号可表示为

其中，hi(p)代表第i个发射天线和接收天线对应的p路径信道系数，w(k)代表零均值方差为σ2w复高斯白噪声，path代表路径的条数。

4 单载波传输下识别方法

目前，在频率选择性衰落信道下，对单载波条件下的空时分组码盲识别算法研究较少。ML法使用最大似然给出了正确识别概率的最优解［8～9］。Vincent Choqueuse和Mlanie Marazin［10］等基于最大似然的方法，提出二阶统计量（second-order statis⁃tic，SOS）算法，实现了对空时分组码的识别。基于Kolmogorov-Smirnov（K-S）检验的识别算法［11］是将接收信号分为相关函数分布不同的2段，通过KS检验其经验累积分布函数之间的距离，达到识别AL-STBC和SM-STBC的目的。Mohamed Marey［12］等在频率选择性衰落信道下，提出利用空时分组码的互相关矩阵在不同时滞下具有波峰这一特性，虚警率识别法（False Alarm Rate，FAR）来识别空时分组码。

4.1K-S识别方法

在接收端，基于K-S检验的识别算法是将接收信号分为相关函数分布不同的2段，假设接收端接收信号序列为

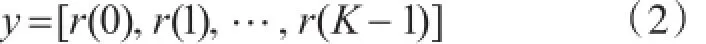
当时延参数τ=1时，如图1所示将接收信号分为不重叠的2段：

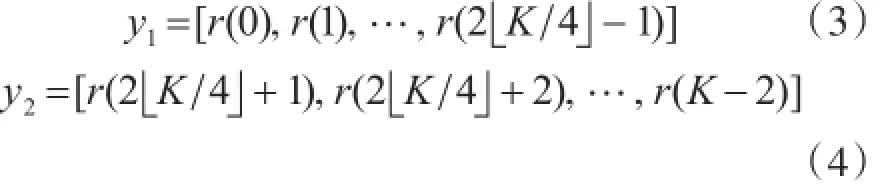
其中，K为接收信号长度，■■.为向下取整函数，即取最接近自变量且比自变量小的整数。

2个信号序列的长度分别为2■K 4■和K-2(■K 4■+1)，其相关函数为

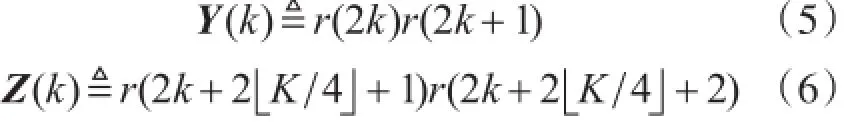
图1 接收信号分为不同的2段

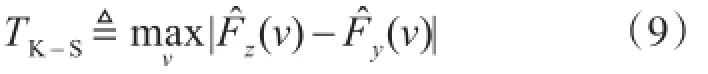
以此作为拟合优度统计值，当TK-S≥λ时，拒绝假设H0，其中

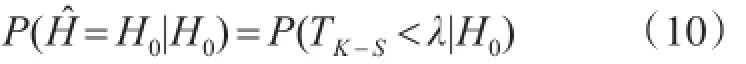
KS算法的识别流程：

1）获取接收信号r，求取Y(k)、Z(k)；

2）求取经验累积分布函数Fy(x)Fz(x)；

3）通过计算Fy(x)Fz(x)之间的最大v距离TK-S，与λ值作比较，达到识别AL-STBC和SM-ST⁃BC的目的。

4.2最大似然识别方法（ML）

假定信道是频率选择性衰落信道，模型为一个nr×nt的矩阵，其中，nr是接收天线的个数，nt是发射天线的个数，且假定精确同步，因此第k个接收块为

WkBv是nr×l维的加性噪声，l代表STBC的时隙数。

因此最大似然函数为

当SM传输的时候，其中Y(k)跟Z(k)是独立同分布的；当AL传输的时候，Y(k)跟Z(k)不一定是独立同分布。通过K-S检验是否同一分布，可以对AL和SM进行区分。

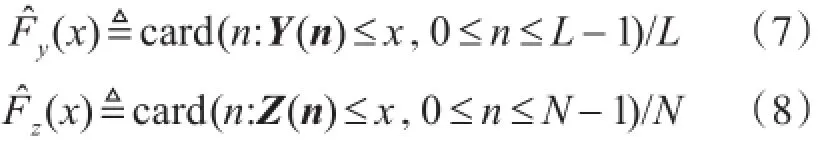
其中Card(.)为指示函数。

Fy(x)，Fz(x)之间的距离可以作为一个特征来识别SM-STBC和AL-STBC，本文中采用了两样本Kolmogorov-Smirnov（K-S）检验来估计两个经验累积分布函数之间的距离。两个经验累积分布函数之间最大距离可表示为

log(Λ|Y|C,X)是Y在通信参数X的条件下最大似然函数。

最大似然算法原理就是在等概率发射符号的先验条件下，找出局部的最大值所对应的STBC类型就是所估计的STBC。

最大似然算法在已知信道信息和噪声功率的条件下能够求得使识别概率的最优解，而在实际的通信传输条件下这往往是不可预知的，因此该算法有很大的局限性。

4.3FAR算法

所提出的FAR识别算法最基本的思想是对峰值检测设置一个边界。如果所检测到的值超出了边界，则是AL-STBC，反之，则检测到的是SM-ST⁃BC。边界函数的值是通过所求的虚警概率函数值确定的，可以检测到传输端是AL还是SM信号。算法的具体流程如下：

峰值检测问题可以用一个二元假设检验，H0为所计算的互相关函数峰值存在，H1为至少存在一个峰值。

由于接收端无法预知信道信息，所以FAR算法利用SM信号互相关函数的统计特性来设定了一个边界值。用向量Λ来表示在q=-Lh,…,Lh时，|Ai,i′(q)|的估计值，Ai,i′(q)是独立的随机复高斯分布，且方差为σi2,i′。向量Λ为独立的瑞利随机分布，其经验累积分布函数可表示如下

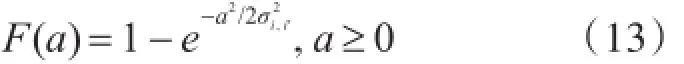
假设β为向量Λ中的最大值，由于随机变量中的累积分布函数的最大值相当于变量中累积分布函数的乘积，β的累积分布函数可表示为

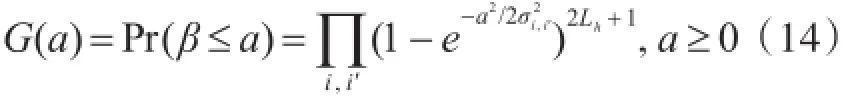
定义η为边界值，则

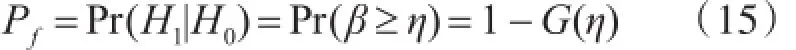
由上述可得，边界值η可表示为

算法识别过程：

2）计算式（16）中的边界值η；

3）计算向量Λ中的最大值β；

4）如果β≥η，则信号为AL-STBC，反之，接受的信号是SM-STBC。

5 多载波传输下识别方法

多载波传输下对空时分组码的盲识别技术，为了抑制频率选择性衰落，设计了一种将高速的信号流分成多个低速的子信号流，在多个相互正交的载波上进行发射的方法，也就是OFDM技术，随着OFDM-STBC技术的发展，主要分为两种方法：时延四阶矩［13～14］和四阶循环平稳［15～16］。

5.1基于时延四阶矩的识别算法

接收信号的时延四阶矩，在接收端的OFDM可表示为

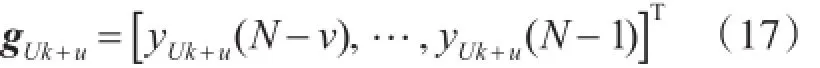
接收OFDM块在时延为τ时四阶矩可表示为

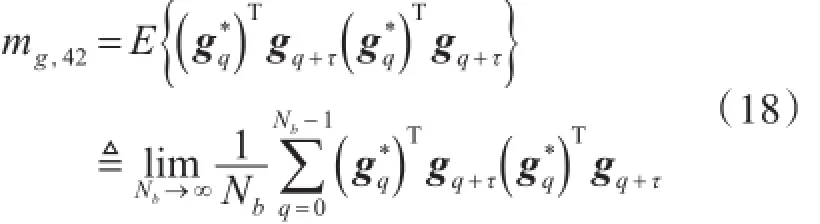
假定数据符号的二阶统计量已知，符号与噪声独立，SM-OFDM的每列信号是相互独立的，因此：

AL-OFDM、ST3-OFDM和ST4-OFDM相应的推导过程如下

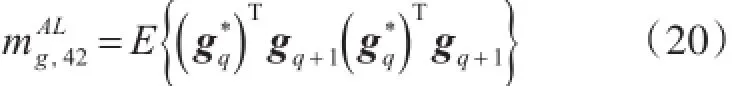
当gq与gq+1不在同一编码矩阵内，两者之间没有相关性，当gq与gq+1在同一编码矩阵内，两者之间存在相关性，因此：

因此发射端mz,42的表达式为

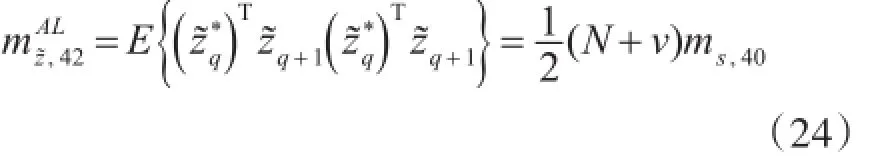
同理对于ST3-OFDM信号，计算接收OFDM块在时延为2时发射端mz,42的表达式为

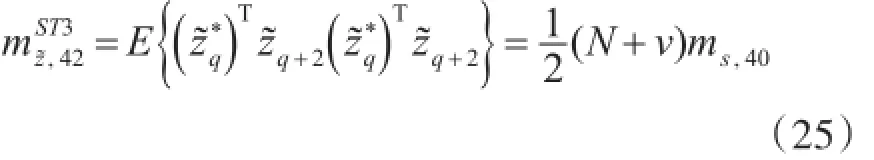
同理对于ST4-OFDM信号，计算接收OFDM块在时延为5时发射端mz,42的表达式为

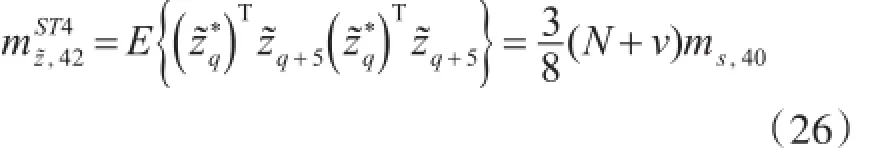
OFDM块的四阶矩mg,42应从有限长度的OFDM块估计：

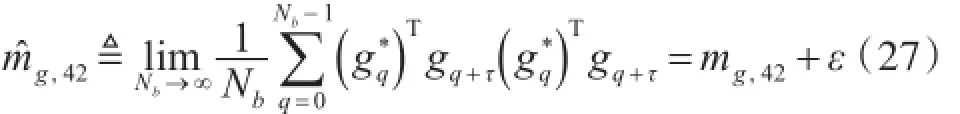
其中，ε代表估计的误差，是一个零均值的随机变量，当Nb→∞，ε→0，τ∈{1,2,5}。

识别待识别STBC-OFDM信号可以由实验值与理论值的最小欧式距离盲识别发射端的编码方式。

算法识别过程：估计时延为1，2，5时的接收OFDM块的四阶矩mg,42；当时延为5时，只有ST4-OFDM信号的四阶矩不为零，可以区分ST4-OFDM信号；当时延为2时，只有ST3-OFDM信号的四阶矩不为零，可以区分ST3-OFDM信号；当时延为1时，只有AL-OFDM信号的四阶矩不为零，可以区分AL-OFDM信号。判断非零性方法为：计算待识别信号四阶矩的估计值与0的欧式距离，距离大的判定为待识别信号，否则为其他信号。

整个算法的流程图如图2所示。

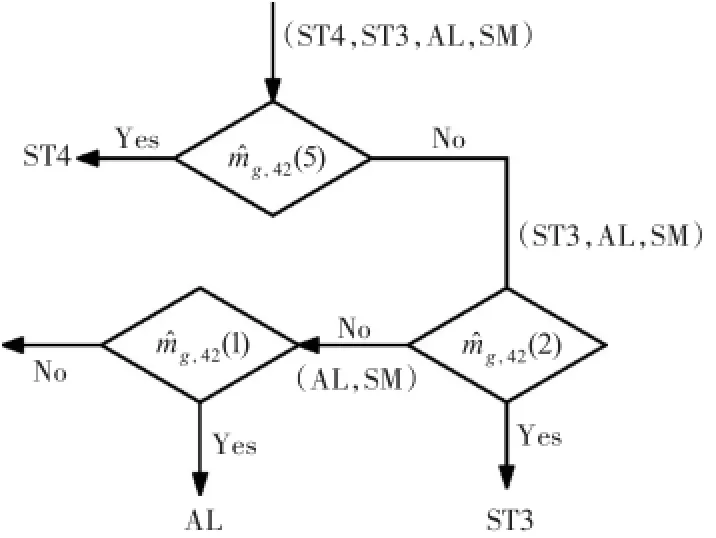
图2 算法流程图

5.2接收信号四阶循环平稳

接收的信号r(k)以长度(N+v)进行分组，分组的向量gUk+u可表示为

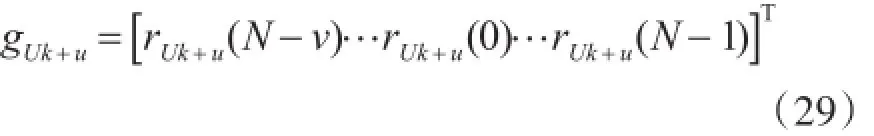
接收的OFDM块G可表示为

其中NB为OFDM块的个数，G是(N+v)×NB维矩阵，每一列代表接收的单个OFDM块。

因此，接收OFDM块在时延向量(0,τ1,τ2,τ3)的四阶矩表示为

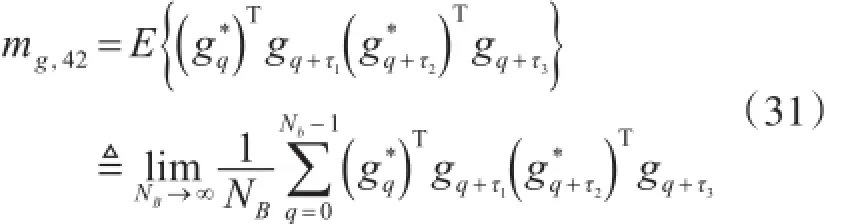
SM-OFDM信号：

对于任意τ，显然有：

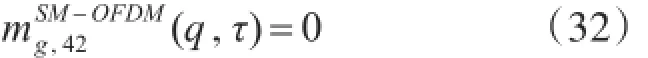
因此，SM没有任何的循环频率。

Al-OFDM信号：

令τ2=0和τ1=τ3=τ，在这里，取τ=1。

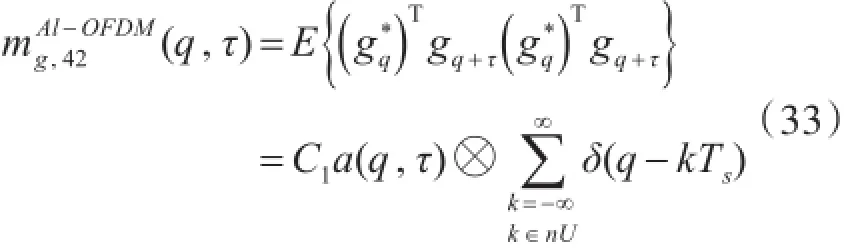
ST3-OFDM信号：

τ=2：

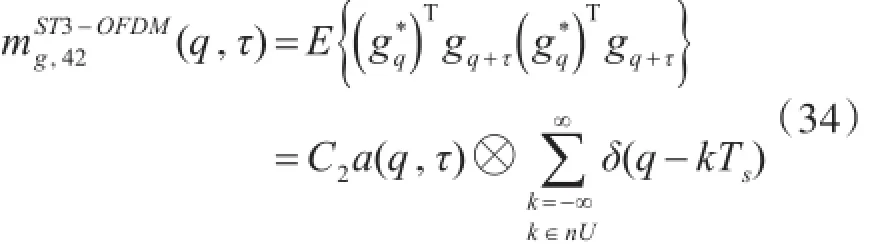
ST4-OFDM信号

τ=5：

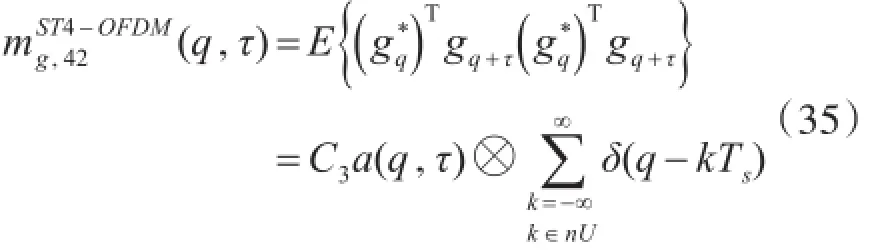
算法识别过程：根据在τ∈{}1,2,5，ST⁃BC-OFDM对应事件的分布情况，以此作为特征参数区分集合，可以用一个决策树表示。

识别的流程图如图3所示。在这里，确定循环频率的存在是通过检测是否存在峰值。

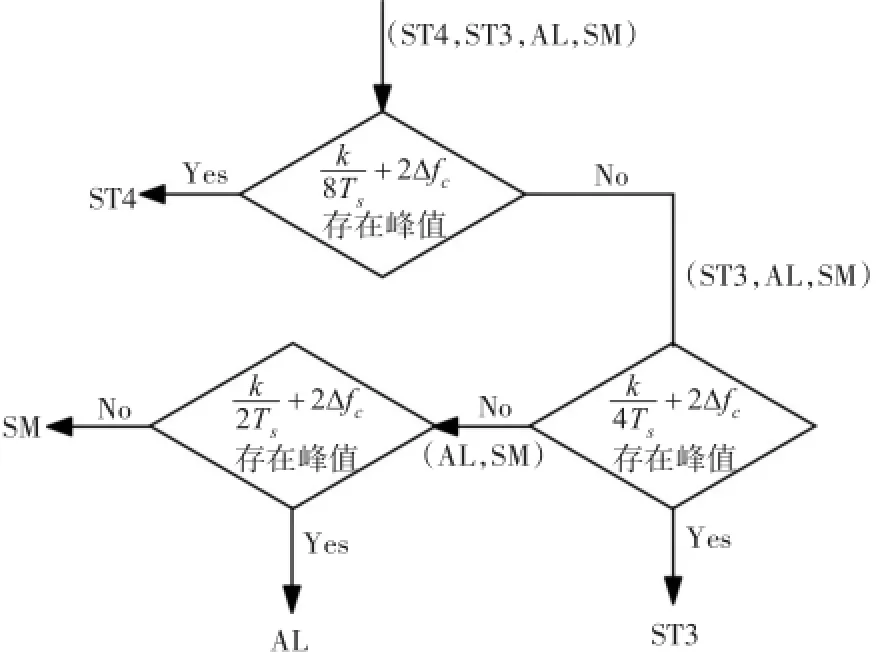
图3 STBC-OFDM识别算法流程图

6 算法性能分析和比较

本节对频率选择性衰落信道下，空时分组码的主要识别算法进行比较。

6.1单载波传输算法性能比较

三种算法的性能比较如图3所示：其仿真信号采用QPSK调制，采用平均识别概率为性能标准，即=∑P(θ=θ|θ)。θ∈{SM,AL}

图4 算法的平均识别概率

ML算法：在低信噪比的情况下，ML算法的识别概率高，但随着信噪比的增加，ML算法的识别概率偏低。ML算法缺点在于需要预先估计信道信息，而且算法的复杂度高、计算量大。

KS算法：在低信噪比的情况下，识别能力较弱，但随着信噪比的提升，识别概率明显提升，该算法计算简单，识别所需要的接受信号采样数少，且适用于单天线条件下识别，具有一定的实用性。

FAR算法：FAR算法的识别性能介于ML算法和KS算法之间，且随着信噪比的提高，识别性能提升显著。算法利用了相关矩阵，且为多天线接收端，互相关性强容易被识别，且计算复杂度较低。

6.2多载波传输识别性能比较

两种算法的性能比较如图4所示：其仿真信号采用QPSK调制，采用平均识别概率为性能标准，即=∑P(θ=θ|θ)。θ∈{SM,AL，STB3，STB4}

四阶时延矩识别算法：该算法在低信噪比下（SNR=0dB），算法的正确识别概率约为1，识别效果理想。该算法不需要噪声信息和信道系数等先验信息，适合于非合作通信场合，且不受载波频偏、时间同步偏差和多普勒频率的影响，具有实用性。

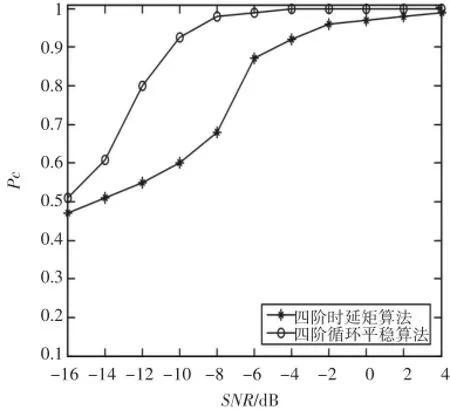
图5 算法的平均识别概率

四阶循环平稳识别算法：该算法在低信噪比下（SNR＜6dB），算法的正确识别概率远好于四阶时延矩算法，信噪比较高时，算法的正确识别概率约为1，识别效果理想，能够满足实际通信环境应用，且算法不需要噪声信息、调制信息和信道系数，适合于非合作通信场合；不受调制方式、载波频偏、时偏和多普勒频偏的影响，具有实用性，适合进一步推广应用。

7 结语

空时分组码的盲识别具有非常广阔的前景，其在频率选择信道下的识别技术更是具有重要意义，是通信信号侦查的热点和难点。

本文总结了单载波、多载波两种传输条件下空时分组码在频率选择信道中的盲识别算法，介绍了其基本原理以及识别的过程。通过仿真对两种条件下的识别算法的性能进行了比较，并简述了其优缺点。目前，虽然空时分组码的技术研究已经取得了很多成果和突破，但该技术的研究还并不完善，还有待研究者更进一步的延伸研究。

［1］Choqueuse V，Koffi Yao，Ludovic Collin，et al.Hierarchi⁃cal space-time block recognition using correlation matrices［J］.IEEETransactiononWirelessCommunication，2008，7（9）：3526-3534.

［2］Choqueuse V，Marazin M，Collin L，et al.Blind recognition of linear space-time block codes：a likelihood-based ap⁃proach［J］.IEEE Transaction on Signal Processing，2010，58（3）：1290-1299.

［3］Eldemerdash Y A，Marey M，Dobre O A，et al.Fourth-or⁃der statistics for blind classification of spatial multiplexing and Alamouti space-time block codes signals［J］.IEEE Transaction on Communication，2013，61（6）：2420-2431.

［4］Marey M，Dobre O A，Inkol Robert.Classification of space-time block codes based on second-order cyclosta⁃tionarity with transmission impairments［J］.IEEE Transac⁃tiononWirelessCommunication，2012，11（7）：2574-2584.

［5］Y.Eldemerdash，M.Marey，O.Dobre，G.Karagiannidis，and R.Inkol.Fourth-order statistics for blind classifica⁃tion of spatial multiplexing andalamouti space-time block code signals［J］.IEEE Trans.Commun.，2013，61（6）：2420-2431.

［6］M.R.De Young，R.Heath，B.L.Evans.Using higher or⁃der cyclostationarity to identify space-time block codes［J］.in Proc.IEEE GLOBE COM，2008：1-5.

［7］V.Choqueuse，K.Yao，L.Collin，and G.Burel.Hierar⁃chical space-time block code recognition using correlation matrices［J］.IEEE Trans.Wireless Common.，2008，7（9）：3526-3534.

［8］Choqueuse V，Koffi Yao，Ludovic Collin，et al.Hierarchi⁃cal space-time block recognition using correlation matrices［J］.IEEE Transaction on Wireless Communication，2008，7（9）：3526-3534.

［9］Choqueuse V，Marazin M，Collin L，et al.Blind recognition of linear space-time block codes：a likelihood-based ap⁃proach［J］.IEEE Transaction on Signal Processing，2010，58（3）：1290-1299.

［10］V.Choqueuse，K.Yao，L.Collin and G.Burel.Hierar⁃chical space-time block code recognition using correla⁃tion matrices［J］.IEEE Transactions on Wireless Com⁃munications，2008，7（9）：3526-3534.

［11］Mohammad karimi M，Dobre O A.Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov（K-S）test［J］.IEEE Com⁃munication Letters，2014，18（10）：1711-1714.

［12］Mohamed Marey，Senior Member.Classification of STBC SystemsOverFrequency-SelectiveChannels［J］. DOI10.1109/TVT.2014.2335415，IEEE Transactions on Vehicular Technology.

［13］Marey M，Dobre O A，Inkol R.Blind STBC identification for multiple-antenna OFDM systems［J］.IEEE Transac⁃tion on Communication，2014，62（5）：1554-1567.

［14］Eldemerdash Y A，Dobre O A，Liao B J.Blind identifica⁃tion of SM and Alamouti STBC-OFDM signal［J］.IEEE Transaction on Wireless Communication，2015，14（2）：972-982.

［15］M.Marey，O.A.Dobre，R.Inkol.Novel Algorithm for ST⁃BC-OFDM Identification in Cognitive Radios［C］//IEEE Global Communications Conference，2013.Atlanta，GA：IEEE，2013：2770-2774.

［16］Karami E E，Dobre O A.Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclosta⁃tionarity［J］.IEEE Transaction Vehicular Technology 2015，64（3）：942-953.

Reviews of Blind Identification of STBC over Frequency-selective Channels

LIN Hongwen1YU Keyuan1ZHONG Zhaogen1LIU Zhao2
（1.Department of Electronic and Information Engineering，Naval Aeronautical and Astronautical University，Yantai264001）（2.Marine Navigation of Rongcheng，Rongcheng264300）

Blind identification of space-time block codes（STBC）is a new important direction in communication signal blind identification technology，especially under the condition of frequency-selective fading channels，which has very important practical significance.Firstly，the significance of blind identification of STBC is introduced.Secondly，the category of STBC blind recognition in single carrier and multicarrier transmission is illustrated.Then，the key of each algorithm is summarized and carried on the con⁃trast.Finally，the difficulties and the future trend of STBC recognition algorithm are indicated.

space-time block code，frequency-selective fading channels，single carrier transmission，orthogonal frequency division multiplexing

TN911.7

10.3969/j.issn.1672-9722.2017.05.013

2016年11月18日，

2016年12月29日

泰山学者工程专项经费（编号：ts201511020）资助。

林洪文，男，博士，教授，研究方向：通信信号识别处理。于柯远，男，硕士研究生，研究方向：信号处理新技术。钟兆根，男，博士，讲师，研究方向：通信信号盲分离与统计信号处理。刘昭，男，助理工程师，研究方向：通信信号处理。