基于GMM非线性变换的说话人识别算法的研究*
罗文华,杨 彦,齐 健,赵 力
(1.江苏盐城工业职业技术学院汽车工程学院,江苏 盐城 224005;2.东南大学信息科学与工程学院,南京 210096)
基于GMM非线性变换的说话人识别算法的研究*
罗文华1*,杨 彦1,齐 健2,赵 力2
(1.江苏盐城工业职业技术学院汽车工程学院,江苏 盐城 224005;2.东南大学信息科学与工程学院,南京 210096)
针对与文本无关说话人识别GMM模型中,某些非目标模型的测试帧的模型得分可能会比较高,从而引起误判的问题。从帧似然概率的统计特性出发,提出了一种GMM非线性变换方法。该方法通过对每帧各模型的得分赋予不同的权值,使得得分高的模型权值大,得分低的模型权值小,由于目标模型得分高的帧要多于其他非目标模型,所以这样可以提高目标模型的总得分,降低非目标模型的得分,从而降低误判的可能。理论推导和实验结果表明,该变换方法能够提高GMM说话人识别的识别率。
与文本无关说话人识别;混合高斯模型;非线性变换
语音是每个人的自然属性之一,由于各个说话人发音器官的生理差异以及后天的发音习惯等行为差异,每个人的语音中蕴含着各个人的个人特征[1]。说话人识别就是着眼于这种个人差异性特征,利用一定的特征描述模型和特征识别方法以达到识别说话人的目的。说话人识别按其被输入的测试语音来分可以分为与文本有关和与文本无关的说话人识别。而与文本无关的说话人识别在今天无疑有着更广泛的应用。由于每个说话人的个人特征具有长时变动性,并且每个说话人的发音与环境、说话时的情绪和健康程度有密切关系,同时实际过程中还可能引入背景噪声等干扰因素,这些都会影响与文本无关说话人识别系统的性能。对此,Tagashira S[2]等人提出了说话人部分空间影射的方法,提取只含有个人信息的特征进行说话人识别,但该方法对于个人信息的长时变动没有达到满意的效果。Liu C S[3]等提出了基于最近冒名者的模型的方法,但因为必须计算所有的冒名者的似然函数,使得计算量的变大。Reynolds[4]提出了基于说话人背景模型的平均似然函数来计算得分;Matsui和Furui[5]提出了基于后验概率的模型。Markov和Nakagawa[6]将整个语句分成若干帧,计算每帧得分,获得总得分,但它没有考虑目标模型和非目标模型的帧似然概率的特性。
目前为止高斯混合模型GMM(Gaussian Mixed Model)仍然被认为是目前较优的与文本无关说话人识别的模型。由于它作为统计模型能够吸收说话人个性特征的变化,可以提高识别性能。但是由于GMM作为统计模型对模型训练数据量有一定的依赖性,所以对于小样本的与文本无关说话人识别系统,要使GMM完全吸收由不同说话人引起的语音特征的变化是非常困难的。所以在实际应用中通常采用话者适应的方法使未知说话人的语音去适应已知标准说话人的语音模型。因此,近年来在说话人识别方法方面,基于高斯混合背景模型GMM-UBM(Gaussian Mixed Model-Universal Background Model)方法已成为主流的识别方法[7]。基于GMM超向量的支持向量机和因子分析方法[8-9]则代表GMM-UBM方法的新成果。其中高斯超向量是由GMM的均值统计量顺序排列而成,由于该特征的维度特别高,所以称为超向量。该特征主要用在基于支持向量机(SVM)的说话人识别系统中,且常与扰动属性投影NAP(Nuisance Attribute Project)或联合因子分析JFA(Joint Factor Analysis)等方法相结合,用于去除语音信号中的信道畸变噪音成分。超向量是一种基于高斯混合模型的高层语音特征,它不但继承了高斯混合模型的鲁棒性,而且还继承了高斯混合模型呈现的说话人发音个性统计信息,是近年来说话人识别领域的研究热点之一。由于高斯混合模型对信道畸变和绝大部分非平稳噪音的鲁棒性并不明显,所以高斯超向量对信道畸变和非平稳噪音的鲁棒性并不理想[10]。因此,一些局部的改进方法和针对不同应用的改进方法也不断被研究和被提出[11-16]。
目前针对基于GMM的说话人识别系统的改进方法的研究大多集中在特征分析和模型优化等前端处理方面,在说话人识别到分统计的后端处理方面,国内外研究的较少。本文根据基于GMM模型的与文本无关说话人识别系统的目标帧和非目标帧似然概率特性,提出了对各模型帧似然概率进行非线性变换,以提高识别率的方法。通过理论分析发现,简单的对帧似然概率进行线性变换不能提高识别率。理论推导和实验分析表明,该变换确实能够提高基于高斯混合模型的与文本无关说话人识别系统的识别率。
1 基于GMM的与文本无关说话人识别方法
为了说明基于非线性变换GMM模型的说话人识别方法,首先必须介绍一下GMM模型以及传统的基于GMM的说话人识别方法。GMM是M成员密度的加权和,可以用式(1)表示[1]:
(1)
式中:X是D维随机向量;bi(X)(i=1,2,…,M)是成员密度;ai(i=1,2,…,M)是混合权值。完整的GMM可表示为:λi={ai,μi,Σi},(i=1,2,…,M)。每个成员密度是一个D维变量的高斯分布函数,形式如下:
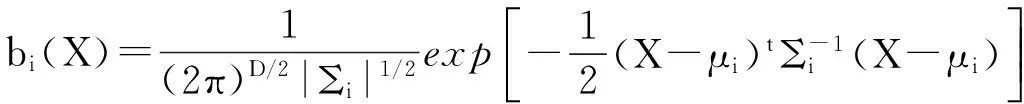
(2)
对于一个长度为T的测试语音时间序列X=(x1,x2,…,xT),它的GMM概率可以写作:
(3)
或用对数域表示为:
(4)
识别时运用贝叶斯定理,在N个未知话者的模型中,得到的似然概率最大的模型对应的话者即为识别结果:
(5)
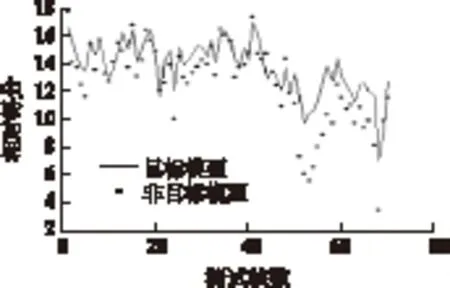
图1 目标模型与某非目标模型的得分情况
可以看出,以上的得分计算是逐帧进行的,一般来说,目标模型得分高的帧要多于其他非目标模型。然而,在我们的研究中发现,由于说话人的个人特征的长时变动或者噪声等干扰的影响,存在一些测试帧对于目标模型的得分小于非目标模型的得分,我们将之称为坏帧,这些坏帧对于非目标模型的得分可能比较高,如果坏帧大量存在的话,非目标模型的得分拉近或者有可能超过目标模型的得分,从而导致了误判。图1给出了某说话人识别实验中目标模型与非目标模型的帧得分情况,从中可看出目标模型的得分高的好帧要多于非目标模型。但是也有某些坏帧的得分大于目标模型的得分。为此,我们的思路是可以通过某些变换对每帧各模型的得分赋予不同的权值,得分越高的模型权值越大,得分越低的模型权值越小,由于目标模型得分高的帧要多于其他非目标模型,所以这样有可能提高目标模型的总得分,降低非目标模型的得分,从而提高识别率。
2 基于帧似然概率非线性变换GMM的说话人识别方法
在基于GMM的说话人识别系统中,对于任一帧矢量xt(t=1,2,…,T),假定λ0为目标用户对应的高斯混合模型,λ1为非目标用户对应的模型,设存在一种线性变换:
f[p(xt|λi)]=ap(xt|λi)+b(a,b为常数)
(6)
则有:
f[p(xt|λ0)]-f[p(xt|λ1)]=ap(xt|λ0)+b-
[ap(xt|λ1)+b]=a[p(xt|λ0)-p(xt|λ1)]
(7)
简单起见,假设a>0(a<0分析类似),可得:
p(xt|λ0)≥p(xt|λ1)⟺f[p(xt|λ0)]≥f[p(xt|λ1)]
(8)
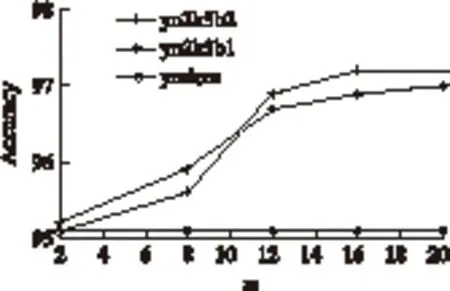
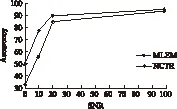
p(xt|λ0) (9) 从上面分析可看出,这样的线性变换没有改变各模型帧得分的相对大小关系,也没有缩小或拉大各模型帧得分差,从而也不可能影响总得分的大小关系。也就是说线性变换不能降低误识率。因此,为了提高识别率,必须采用非线性变换。而且对于选择的GMM帧似然概率的非线性变换应该满足以下几点要求: (1)使同一说话人的各个时刻的得分差减小。 (2)使同一时刻t(0≤t≤T)不同说话人的得分差增大。 (3)不改变同一时刻各帧得分值的相对大小。 对此,本文提出了一种非线性变换f(p(xt|λi),t,i),(0≤t≤T,0≤i≤N),它的定义如下: 计算其得分: (10) 计算当前时刻的前K个时刻该模型的得分均值: (11) 作为S(xt,λi)的补偿,令: S′(xt,λi)=S(xt,λi)+mt,iδ[S(xt,λi)- (12) 式中: mt,i∈[0,1),δt,i= 则最后各模型的总得分为: (13) 我们称以上的变换为归一化补偿变换。下面我们来分析该变换的特性。为简单分析起见,令只存在两个模型λ0,λ1,其中λ0为目标模型。任取连续两帧进行分析,即T=2: (14) (15) 在GMM中,当S(X|λ0)>S(X|λ1)判为λ0,如果不采用任何变换: lnP(x1|λ0)+lnP(x2|λ0)>lnP(x1|λ1)+lnP(x2|λ1)⟹ P(x1|λ0)P(x2|λ0)-P(x1|λ1)P(x2|λ1)>0⟹ P(x1|λ0)nP(x2|λ0)n-P(x1|λ1)nP(x2|λ1)n>0 (16) 而对于归一化补偿变换: (17) (1)P10=1且P20=1时,即两帧都是目标帧得分高,则式(16)可为: P11P21<1 (18) 式(17)可为: S(X|λ0)-S(X|λ1)= (19) 假设式(19)的两项都大于0,则可得: (20) 式中:实际过程中为保证第2、第3项对第1项的影响比较小,m的取值为远小于1的正数。下面来分析第1项: (21) 由于p11<1,p21<1,p11p21<1,与式(16)相比,式(21)能较大地拉开目标模型与非目标模型的得分差,当m的取值为远小于1的正数时,式的第2、第3部分对第1部分的影响比较小,不会改变相对大小。因此,采用归一化变换后的两个模型的总得分的相对距离拉大了。 (2)P′(x1|λ0)=1且P′(x2|λ1)=1时,即第1帧目标模型得分高,第2帧非目标模型得分高,则式(16)可为: p20-p11>0 (22) 式(17)可为: (23) 假设式(23)的两项都大于0,则可得: (24) 式(24)第1项为: (25) (3)当P′(x1|λ1)=1且P′(x2|λ0)=1时,即第1帧非目标模型得分高,第2帧目标模型得分高时,分析与(2)类似。 从上面的分析可得出,归一化补偿变换能够拉大目标模型与非目标模型的相对得分比,同时也拉近了同一模型各帧得分值,使得各模型的帧得分值不仅与当前时刻有关,而且还与前K个时刻有关。参数m的选取对得分结果有着很大的影响,必须适当选取,为了计算方便我们在实际过程中选为百分之一的整数倍。 对于函数f(x)=xn/(xn+b)而言,参数n越大,曲线在区间[0,1]内越陡,也就是说对应于不同的x,f(x)的差值将拉得更大;参数b的越大,曲线越平坦。 对于归一化补偿变换而言,参数n的值不能很大,否则计算量很大,一般取参数n=2~5;参数b一般取大于1并且靠近1的值。参数K的选取对帧得分值的相对位置也有影响,过大导致计算复杂,过小影响稳健性,一般K选取为2~5。 通过上面的分析,归一化补偿变换具有了非线性变换的3个要求,与线性变换相比,可以进一步降低误识别率。 语音数据为在实验室内录制的语音,采样频率是8 kHz,采样位数8 bit,共20人(青年男女),每人40句不同的话作为纯净语音,在纯净语音上叠加高斯白噪声和非平稳噪声(噪声源由英国TNO感知学会所属的荷兰RSRE语音研究中心提供)。数据每帧帧长N=256,50%的帧重叠。选取12阶MFCC倒谱参数作为说话人识别的特征参数。 图2给出了混合数M=16时采用归一化补偿变换的GMM的识别率。令m′=100m。由图2可以看出,与不采用变换相比,归一化变换可以得到比较高的识别率。当n,K,b一定时,随着m′参数的增大,归一化变换的识别率相应增加,同时我们注意到,当m′值超出一定范围后,识别率增加趋缓,因此合理选择参数m′,可以进一步提高识别率。 图2 同一时期归一化变换识别率 实验1是在无噪声环境下给出的,为了在噪声环境下测试归一化补偿变换的性能,我们进行了实验2。识别结果如图3所示。 图3 20名说话人的平均识别率(%) 图3中归一化变换的参数为n=3,K=4,b=1.1,m′=8。由图3可以看出,虽然在信噪比增加的情况下,未经过归一化变换和经过归一化变换处理的识别率都会增加,并在信噪比提高到一定程度之后,识别率增加趋势变缓。但是,在信噪比较低的情况下,归一化补偿变换的识别率要比未经过归一化变换识别率提高很多。由此可见归一化变换处理的方法提高了基于GMM的与文本无关的说话人识别的识别率。 在基于GMM的与文本无关的说话人识别中,实际环境和个人因素一直是影响识别率提高的原因,大多数研究集中在前端处理,但在说话人识别后端处理方面,国内外研究比较少。本文从各模型帧似然概率的统计特性出发,分析了线性变换不能够提高识别率,并提出了一种新的非线性变换方法——归一化变换。理论分析和实验结果表明,与GMM常用的最大似然变换相比,归一化变换能够拉大目标模型与其他非目标模型的帧得分比。因此,我们认为该变换能够提高与文本无关说话人识别系统识别率。 [1] 赵力. 语音信号处理[M]. 北京:机械工业出版社,2003:236-253. [2] Tagashira S,Ariki Y. Speaker Recognition and Speaker Normalization by Projection to Speaker Subspace,IEICE,Technical Report,1995,SP95-28,25-32. [3] Liu C S,Wang H C. Speaker Verification using Normalization Log-Likelihood Score[J]. IEEE Trans. Speech and Audio Precessing,1980,4:56-60. [4] Douglas A Reynolds. Speaker Identification and Verification Using Gaussian Mixture Speaker Models[J]. Speech Communication,1995,17:91-108. [5] Matsui T,Furui S. Concatenated Phoneme Models for Text Variable Speaker Recognition[C]//Proc IEEE Inter Conf on Acoustics,Speech,and Signal Processing(ICASSP’93)1993:391-394. [6] Markov Knakagawa S. Text-Independent Speaker Recognition System Using Frame Level Likelihood Processing[J]. Technical Report of IEICE,1996,SP96-17:37-44. [7] Dehak N,Dehak R,Kenny P,et al. Comparison between Factor Analysis and GMM Support Vector Machines for Speaker Verification[C]//The Speaker and Language Recognition Workshop(Odyssey 2008). Stellenbosch,South Africa:ISCA Archive,January 2008:21-25. [8] Campbell W M,Sturim D E,Reynolds D A,et al. SVM Based Speaker Verificationusing a GMM Supervector Kernel and NAP Variability Compensation[C]//IEEEInternational Conference on Acoustics,Speech and Signal Processing. Toulouse:IEEE,2006,1:97-100. [9] Ferras M,Shinoda K,Furui S. Structural MAP Adaptation in GMM Super Vector Based Speaker Recognition[C]//IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP). Prague:IEEE,2011:5432-5435. [10] Yessad D,Amrouche A. SVM Based GMM Supervector Speaker Recognition Using LP Residual Signal[C]//Image and Signal Processing. Sichuan,China:Springer,2012:579-586. [11] Yadav R,Mandal D. Speaker Recognition:A Research Direction[J]. InternationalJournal of Advances in Electronics Engineering,2012,1(1):87-93. [12] Bousquet P M,Matrouf D,Bonastre J F. Intersession Compensation and Scoring Methods in the i-Vectors Space for Speaker Recognition[C]//International Conferenceon Speech Communication and Technology. Azerbaijan,Baku:IEEE,2011:485-488. [13] Karafi′at M,Burget L,Matejka P,et al. iVector-Based Discriminative Adaptation for Automatic Speech Recognition[C]//IEEE Workshop on Automatic Speech Recognitionand Understanding(ASRU). HAWAⅡ:IEEE,2011:152-157. [14] Lei Y,Burget L,Scheffer N. Bilinear Factor Analysis for iVector Based Speaker Verification[C]//Interspeech Portland,OR,USA:ISCA,2012,2:1588-1591. [15] Rao W,Mak M W. Boosting the Performance of I-Vector Based Speaker Verificationvia Utterance Partitioning[J]. IEEE Transaction on Audio,Speech,andLanguage Processing,2013,21(5):1012-1022. [16] Lei Y,Burget L,Ferrer L,et al. Towards Noise-Robust Speaker Recognition Using Probabilistic Linear Discriminant Analysis[C]//IEEE International Conferenceon Acoustics,Speech and Signal Processing(ICASSP). Kyoto,Japan:IEEE,2012:4253-4256. [17] Reynolds D A,Rose R C. Robust Text-Independent Speaker Identification Using Gaussian Mixture Speaker Models[J]. IEEE Trans on Speech and Audio Processing,1995,3(1):72-83. [18] Matsui T,Furui S. Likelihood Normalization for Speaker Verification Using a Phoneme- and Speaker-Independent Model[J]. Speech Communication,1995;17(1-2):97-116. Text-Independent Speaker Recognition Using GMM Non-Linear Transformation* LOUWenhua1*,YANGYan1,QIJiang2,ZHAOLi2 (1.YanchengInstitute of Industry Technology,Yancheng Jiangsu 224005,China;2.School of Information Science and Engineering,Southeast University,Nanjing 210096,China) For the text independent speaker recognition GMM model,some non-target models of the test frame of the model score may be relatively high,thus causing the problem of false.Based on the statistical properties of the frame likelihood probability,a GMM nonlinear transformation method is proposed.This method gives different weights to each frame model,which makes the model with high score and low weights,as the target model score higher than other non target frame model,so it can improve the total score of the target model,reduce the score of non target model,thus reducing the possibility of false positives.Theoretical results and experimental results show that the proposed method can improve the recognition rate of GMM speaker recognition. text-independent speaker recognition;Gaussian mixture model;non-linear transformation 项目来源:国家自然科学基金项目(61301219);2014年青蓝工程资助项目;2015年农业科技创新专项引导资金项目;2015年盐城市农业科技指导性项目(YKN2015031) 2016-05-10 修改日期:2016-06-09 TN912.3 A 1005-9490(2017)03-0545-06 C:6130;1160 10.3969/j.issn.1005-9490.2017.03.006
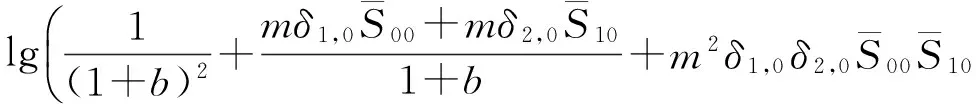

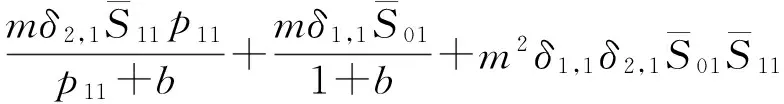
3 实验结果与分析
4 小结


