基于量子滤波器的电能数据检测与分析

吴浩瀚，蒋刚



基于量子滤波器的电能数据检测与分析

吴浩瀚，蒋刚

（国网广安供电公司信息通信分公司，四川广安638099）

随着以智能电表为核心的智能电网快速发展，电力大数据吸引了用户、用电企业、政府的注意力。用电数据容易受到各种未知的随机干扰。探索了将自适应滤波技术引入电网信息监测。而由于用电负荷曲线复杂、不能给出一个具体的模型，利用量子递归神经网络构造了一个与模型无关的智能滤波器。最后提出了利用量子滤波器进行电力负荷预测以及利用测量误差的概率密度函数进行用户异常用电检测的设想。

智能电网；用电信息检测；现代滤波；量子计算

1 引言

经济全球化、化石能源的消耗以及生态日益严峻等必然需要能源的全球化配置。电能由于其清洁、高效、易于传输等特点是一种很好的能源配置介质。智能电网技术是电能优化配置的保障；智能电表是智能电网的重要组成部分，具有用户用电信息采集、原始处理、用电信息存储、双向多费率计算、用户端控制以及双向通信等功能。供电方可以每隔15 min读取一次用户用电数据，如此高频率的数据采集产生了用电大数据，通过对这些用电数据进行数据挖掘，可使客户、供电公司、政府以及社会受益[1]。数据质量是数据挖掘的基础，又由于可用于数据挖掘的电力数据容易受到各种随机干扰，使得原始采集数据不能真实反映客观规律，这就需要对数据进行过滤。由于用户用电负荷曲线复杂，不能给出一个特定的模式进行统一描述；测量噪声虽然大部分是高斯噪声，但也可能伴有其他随机噪声。所以需要一个既与观测数据模型无关，又与噪声统计特性无关的实时智能随机滤波器对用电数据进行实时过滤。目前只有量子滤波器满足智能滤波的要求。

量子滤波器是在量子神经动力学的基础上由Dawes R L[2]于1990年提出的，他给出了利用薛定谔方程进行任意观测信息动态建模的理论解释以及量子随机滤波器的运算框架，但他没有给出薛定谔方程势函数的构造方法，同时由于当时运算能力的限制，量子滤波器没有引起人们的重视。Behera L等人[3]分别采用线性神经网络和RBF神经网络构造势函数，第一次实现了量子滤波算法，并用一些简单信号对滤波器性能进行了比较测试。Ghandi V等人[4,5]对量子滤波器进行了若干改进，并将它们应用于肌电信号增强、脑电信号增强等领域，再进行特征提取并分类。参考文献[6]将量子滤波器应用于通信信号处理。参考文献[7]将量子滤波器应用于语音信号增强。

最后本文再给出两种基于量子滤波器对用电数据分析的新思维：通过将外影响因素加到薛定谔方程的势函数上进行电力负荷预测；通过对测量噪声概率密度函数进行估计实现对用户用电状态的估计。

2 智能电表用电信息在线采集

用户用电信息通过安装在用户侧的采集系统（如智能电表）进行采集，并通过无线、电力线通信、电力光纤等方式回传至供电公司，如图1所示。

目前主要使用GSM无线设备进行用电信息回传。由于智能电表自身的误差、采集过程的测量误差、量化误差、传输过程中容易受到噪声干扰、信道衰落的干扰以及用电客户本身的负荷波动，使得供电公司收到的用电信息具有一定的随机性；同时由于用户用电过程中一些异常现象、雷电影响等使得用电信息本身出现一些突发性变化。这些都对后续数据挖掘造成一定的干扰，不能真实地反映客观规律。这时就需要采用随机滤波器对采集信号进行实时过滤。最好的随机滤波器是卡尔曼滤波器，然而由于卡尔曼滤波器要求观测信号的模型是线性的且噪声为高斯噪声。由于用电用户的用电规律极其复杂，不能用某一个具体的模型归纳，其受到的干扰也不一定全是高斯噪声（如量化噪声就是均匀噪声），这些都限制了以卡尔曼滤波器为代表的传统随机滤波器的使用。近些年开始进入人们视线的量子滤波器能够完成该任务。

3 量子滤波器

3.1 随机滤波问题

随机滤波就是从被随机噪声干扰的观测信号中实时提取感兴趣的量，考虑维观测随机过程：

(2)

其中，()为测量噪声（滤波主要过滤的目标）。要达到转化目标，需要预先假设一个状态变量随时间的演化模型：

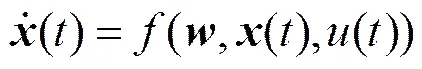
(4)

对观测变量进行估算。其中，()为测量噪声（滤波主要过滤的目标）。注意这里假设的式(3)不一定是真实的状态式(2)，所以存在状态噪声，当假设的模型与真实模型一致时，()=0。只有当假设的模型与真实模型相同或很接近时，这样的转换才有意义。当完全不知道真实模型时，传统随机滤波方法（包括所谓的粒子滤波）不能实现。

3.2 量子神经动力学与量子滤波

当客观系统状态模型未知时，将客观系统的状态变量抽象为生物观测者的意识流，并假设意识具有量子现象，其状态演化满足薛定谔方程[9]：

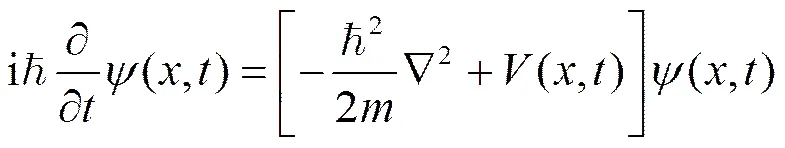
(6)

这样就不需要知道观测信号的模型和测量噪声的统计类型，实现了智能滤波。

量子滤波器实现的关键是将输入观测信号如何映射为薛定谔方程中的势函数，目前都是采用神经网络方法，采用参考文献[10]设计的滤波器结构，其滤波结构如图2所示。

薛定谔方程的势函数结构为：

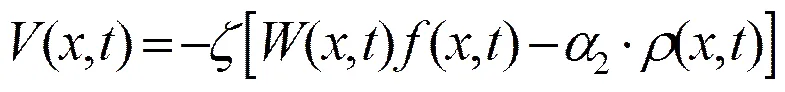
其中：

(8)

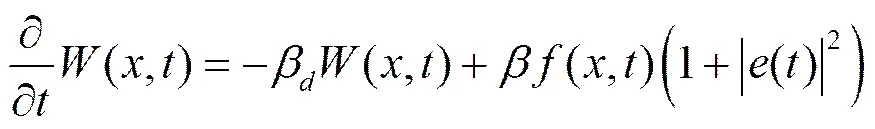
(10)

上述各式中的参数可以通过遗传算法搜索得到。

3.3 滤波效果测试

假设原始信号受到非平稳加性高斯白噪声干扰，原始信号是正弦信号。分别用量子滤波器和递归最小二乘滤波（recursive least square，RLS）器对观测信号进行过滤，其效果如图3、图4所示。

对比图3和图4可以发现，量子滤波器滤波结果更加接近真实信号、更加光滑但是时延比RLS（特殊的卡尔曼滤波器）结果更大。这是由于RLS强制采用线性模型描述观测信号，这就使得状态噪声比较大，导致滤波不准确；而量子滤波器与观测信号模型无关，没有状态噪声。由于量子滤波器是一个基于量子神经网络的自适应滤波器，它实质是模拟生物智能的认知方式，使得它的处理速度相对较慢，这也是量子滤波器的缺点。

4 基于量子滤波器的电力数据挖掘

通过量子滤波器采集得到的用电数据可进行如电力负荷预测、异常用电检测等分析。如果采用传统方法，如回归分析、指数平滑以及加权迭代最小二乘法等，进行负荷预测需要对数据进行二次处理，使得量子滤波器速度慢的缺点被放大，且这样并没有完全发挥量子滤波器的性能。由于量子滤波器不含有状态噪声、滤波结果较为准确，可以较为准确地提取出测量噪声，可以利用测量噪声概率密度函数来探究异常用电现象。

4.1 用电负荷预测

量子滤波器可以抽象为图5所示。

稍加改进就可以构成任意预测器如图6所示。

即步前向预测中，每一步观测输入都是前一次预测输出，误差输入为本次预测输出与初始输入之差。由于存在一些可预见性外部事件，如国民经济增长水平、可替代能源增长水平、区域经济发展、用户自身特性变化等，所以需要根据这些外部条件对误差进行重调整，其调整模型有待于进一步研究与探索。图7为某水泥厂2015年负荷曲线，可以看到受到的随机干扰比较大；虚线为量子滤波器过滤后的负荷曲线，除了2月份负荷曲线近似具有周期性且7、8月份平均用电量略低。虚线的末端是利用图6所示算法进行的负荷预测。

4.2 基于测量噪声概率密度函数估计的分析

当前检测用户异常用电的方法已经很多，但是对于如扩差窃电等异常用电信息检测，通过对检测的“真实信号”进行挖掘较难发现[11]。由于量子滤波器状态方程不含有状态误差，所以测得的测量误差是检测设备、传输设备等的固有误差的总和，可以将其看作设备的固有属性，若其概率密度函数发生改变，则可以推断检测、传输信道发生了改变或用户用电习惯发生的变化。测量噪声概率密度函数估计可将观测信号与估计信号作差然后利用Pasen窗核估计法进行计算[12]。图8为某水泥厂上、下半年负荷测量噪声对比曲线，可以发现其概率密度函数都是高斯函数——符合大数定理，上下半年概率密度函数相当且方差都相对较大。

图9为某天然气厂2015年上、下半年负荷测量噪声概率密度函数，相对图8中所示水泥厂的负荷噪声方差小很多。

对比图8和图9还可以发现，测量噪声更多的是客户自身的负荷噪声，即：由测量仪器和传输设备及通道引起的噪声其实很小。如生产和管理都相对粗狂的水泥厂的噪声方差较生产和管理都相对精细的天然气厂更大。所以不同行业之间的概率密度函数具有差异性，同行业之间生产和管理精细化水平也会反映在噪声概率密度函数上。注意，这里的测量噪声是广义的测量噪声，它是相对于可用于数据挖掘的信号，而不是由测量设备和传输设备引起的狭义测量噪声。

5 结束语

智能电网时代，以智能电表为代表的数据采集系统为电力大数据分析奠定了基础，准确采集数据是进行数据挖掘的前提。本文提出了利用实时随机滤波器对用电数据进行在线检测与过滤。利用量子随机滤波器以适应用户负荷曲线模式不定、干扰噪声统计特性未知难题并通过仿真验证了量子滤波器对于传统随机滤波器的优越性。最后本文还利用量子滤波器天然的递推性设计了一种新的负荷预测机；利用量子滤波器不含模式噪声的特点，提出了利用测量噪声概率密度函数进行异常用电检测的方法。

下一步工作要研究各种测量噪声的特征概率密度函数与用户用电方式的对应关系，建立它们之间的模型；另一方面是：利用量子滤波器进行负荷预测中确定宏观预测与预测误差之间的关系。

[1] 王亚东,高岩,金峰. 智能电表数据分析及应用综述研究[J].信息技术, 2015, 18(2):64-68.

WANG Y D, GAO Y, JIN F. Review of smart watthour meter data analysis and applications[J]. Information Technology, 2015, 18(2):64-68.

[2] Dawes R L. Quantum neurodynamics: neural stochastic filtering with the schroedinger equation[C]//1992 International Joint Conference on Neural Networks, June 7-11, 1992, Baltimore, USA. New Jersey: IEEE Press, 1992:133-140.

[3] Behera L, Kar I. Quantum stochastic filtering[C]//2005 IEEE International Conference on System, Man and Cybernetics, October 10-12, 2005, Hawaii, USA. New Jersey: IEEE Press, 2005.

[4] Gandhi V, McGinnity T M. Quantum neural network based surface EMG signal filtering for control of robotic hand[C]//2013 International Joint Conference on Neural Networks, August 4-9, 2013, Dallas, USA. New Jersey: IEEE Press, 2013:1-7.

[5] Gandhi V, Prasad F, Coyle D H, et al. Quantum neural network-based EEG filtering for a brain-computer interface[J]. IEEE Transactions on Neural Networks and Learning System, 2014, 25(2):278~288.

[6] 朱仁祥, 吴乐南. 用于通信信号非线性时域滤波的量子随机滤波器(英文)[J]. 东南大学学报(英文版), 2007,23(1):22-25.

ZHU R X, WU L N. Quantum stochastic filters for nonlinear time-domain filtering of communication signals[J]. Journal of Southeast University(English Edition), 2007,23(1):22-25.

[7] 赖联有,金福江,吴浩瀚.语音信号的量子随机滤波降噪方法[J]. 信息与控制, 2015, 44(5):598-603.

LAI L Y, JIN F J, WU H H. Speech de-noising method using quantum stochastic filter[J]. Information and Control, 2015, 44(5):598-603.

[8] Busy R S. Linear and nonlinear filtering [J]. Proceedings of the IEEE, 1970,58(6):854-864.

[9] COHEN-TANNOUDJI C, DIU B, LALOE F. 量子力学[M]. . 刘家谟,陈星奎,译. 北京:高等教育出版社, 2014.

COHEN-TANNOUDJI C, DIU B, LALOE F. Mecanique quantique[M]. Translated by LIU J M, CHEN X K. Beijing: Higher Education Press, 2014.

[10] 吴浩瀚,金福江,赖联有,等.基于薛定谔方程的随机滤波算法(英文)[J]. 自动化学报, 2014,40(10):2370-2376.

WU H H, JIN F J, LAI L Y, et al. A stochastic filtering algorithm using SchrÄodinger equation[J]. Acta Automatica Sinica, 2014, 40(10):2370-2376.

[11] 程梅花,李晓明,黄军高,等. 电能量计量计费系统的窃电检测[J]. 电力自动化设备,2002, 22(6): 64-67.

CHENG M H, LI X M, HUANG J G. Filching detection in electric energy measuring and billing system [J]. Electric Power Automation Equipment, 2002, 22(6): 64-67.

[12] Parzen E. On estimation of a probability density function and mode[J]. The Annals of Mathematical Statistics, 1962, 33(3): 1065-1076.

Detection and analysis of energy data by using quantum filter

WU Haohan, JIANG Gang

Communication Company of State Grid Guang’an Electric Power Supply Company, Guang’an 638099, China

With the rapid development of smart power grid as the core of smart meters, power big data has attracted the attention of users, power companies and the government. The introduction of adaptive filtering into the power grid information monitoring was explored. Due to the complexity of the power load curve, specific model cannot be described. A model-independent intelligent filter was constructed by using the recurrent quantum neural network. The quantum filter was tried to use in the power load forecasting and abnormal electrical testing.

smart grid, power information detection, modern filter, quantum computation

O455

A

10.11959/j.issn.1000−0801.2017070

2016−01−25；

2016−03−06

吴浩瀚（1988−），男，现就职于国网广安供电公司信息通信分公司，主要研究方向为现代滤波理论尤其是量子滤波。

蒋刚（1970−），男，国网广安供电公司信息通信分公司高级工程师、经理，长期从事电力系统自动化、信息、通信应用研究与管理方面的工作。