风电与电动汽车协同并网调度环境及经济模型

施泉生, 邸 超, 孙佳佳, 张圣富, 李士动

(1.上海电力学院 经济与管理学院, 上海 200090; 2.国网泰安供电公司, 山东 泰安 271000)

风电与电动汽车协同并网调度环境及经济模型

施泉生1, 邸 超1, 孙佳佳1, 张圣富2, 李士动2

(1.上海电力学院 经济与管理学院, 上海 200090; 2.国网泰安供电公司, 山东 泰安 271000)

建立了风电与电动汽车协同并网环境及经济优化调度模型.采用Weibull分布模拟风速进而得出风电出力,用蒙特卡罗模拟法模拟出定量电动汽车不同V2G模式下的充放电功率.调度风电与电动汽车协同入网,车主响应系统调度并满足与风电、负荷时空互补性,最大程度地消纳风电、减小负荷曲线的波动.以火电机组的运行成本和SO2排放量最小化为目标,应用改进粒子群多目标优化算法求解模型,在Matlab环境下仿真分析比较电动汽车不同V2G模式和入网数量对机组优化结果的影响.

风电; 电动汽车; Weibull分布; 蒙特卡罗模拟

近几年来,电力发展的重要方向是节能减排,风电和电动汽车在环境与经济上的巨大优势受到学者们的广泛关注[1].但风电出力具有波动性和反调峰性特点,并网会影响电力系统的稳定运行.在负荷低谷期,系统调峰容量不足将产生弃风问题[2-3].

目前,我国电动汽车的发展已进入快车道,受车主出行习惯影响,电动汽车大量入网后负荷高峰时段充电,将增大峰谷差和系统压力[4-5].通过调度风电与电动汽车协同并网,实现其与负荷的时间互补性,能有效地解决弃风问题,提高系统的经济效益和环境效益[6-8].

风电与电动汽车并网调度的研究已取得了一些成果.文献[8]建立了调度风电与电动汽车入网的减排模型,并证明了协同调度在促进风电消纳和碳减排方面的作用.文献[9]通过转换系数,建立了以CO2排放量和火电机组发电成本加权值最小为目标的模型.文献[10]建立了以火电机组发电成本最小为目标,电动汽车和风电协调入网经济调度模型.

以上文献采用的模型在电动汽车和风电并网优化调度方面做出了一定的贡献,但没有考虑风电和电动汽车协同并网优化调度的环境和经济的综合效益.

本文提出了风电和电动汽车协同并网优化调度的经济及环境模型.首先,采用Weibull分布模拟风速,进而建立风电出力模型,通过蒙特卡罗模拟定量电动汽车不同入网模式负荷功率.然后,分别以火电发电机组运行成本和SO2排放量最小为目标构建经济及环境优化调度模型,并根据相应约束条件分析了风电接入及电动汽车不同入网模式对机组运行成本和SO2排放的影响.再采用改进粒子群优化算法对模型进行优化求解.最后,在Matlab环境下对模型及优化算法进行仿真分析.

1 风电出力预测

设风速服从Weibull分布[11],则其概率密度函数为:

(1)

式中:v——实时风速;s,q——与风速特性相关的参数.

风电机组出力与风速有关,则用分段函数表示为:

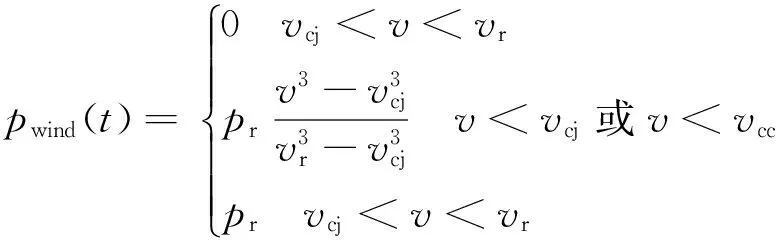
(2)

式中:pwind(t)——风电机组t时刻的实际输出功率;

pr——其额定输出功率;

vcj,vcc,vr——切入风速,切出风速,额定风速.

2 电动汽车V2G模式功率需求模型

无序V2G模式是指电动汽车充放电起始时刻不受外界激励影响,由车主出行习惯决定;有序V2G模式是指电动汽车充放电起始时刻响应系统的调度.车主出行习惯的假设如表1所示.

表1 车主出行习惯的假设

2.1 无序V2G模式功率需求模型

2.1.1 充电模型

无序V2G模式下,车主选择充电时间服从正态分布[13].设变量ζt0为1,表示t0时刻电动汽车正在充电;ζt0为0,表示t0时刻未进行充电,则:

(3)

(4)

式中:tSC——开始充电时刻;tchg——电池连续充电时长;Fwst C——无序V2G模式下开始充电时刻与充电时长的概率分布函数;

pgt0——t0时刻充电功率需求的期望值,pgt0=ζt0pcd.

2.1.2 放电模型

由表1中的假设5可知,无序V2G模式下车主开始放电时刻在[9,17]上服从均匀分布,则无序V2G模式下t0时刻放电功率期望函数表达式为:

(5)

(6)

式中:pdt0——t0时刻的放电功率;tSD——开始放电时刻;tchd——连续放电时长;Fwstf——开始放电时刻tSD与放电时长tchd的概率分布函数.

应用蒙特卡洛模拟法,在每个时间点选10 000个样本,得到无序V2G模式下单台家用电动汽车在1天内每个时刻充放电功率曲线如图1所示.

图1 无序V2G模式下单台电动汽车充放电功率曲线

2.2 有序V2G模式功率需求模型

2.2.1 充电模型

车主响应系统需求,开始充电时刻tSC为:

(7)

式中:tc1,tc2——系统负荷谷期的起止时刻;Tg——谷期时长;k——[0,1]随机数.

2.2.2 放电模型

有序V2G模式下,负荷高峰时期进行放电,则开始放电时刻tSD满足:

(8)

式中:td1,td2——1天内负荷峰段起止时刻;Tf——峰段时长.

电动汽车有序V2G模式下充放电功率模型见文献[14].应用蒙特卡洛模拟法,得到有序V2G模式下单台家用电动汽车1天内每个时刻充放电功率曲线如图2所示.

图2 有序V2G模式下单台电动汽车充放电功率曲线

3 协同并网的环境与经济模型

3.1 目标函数

本文通过电动汽车与风电协调入网,以减少火电机组出力和系统负荷波动.以火电机组SO2排放和运行成本最小化为目标,其中运行成本包括机组的启停成本和燃煤成本两个部分.

(1) 目标函数1 负荷方差为:

(9)

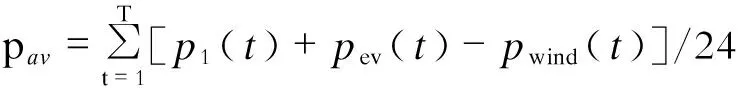
(2) 目标函数2 火电机组运行成本最小为:

(10)

(3) 燃煤成本 燃煤成本为:

(11)

式中:ai,bi,ci——第i个火电机组的燃煤成本系数.

(4) 启停成本 启停成本为:

(12)

(13)

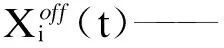
(5) 目标函数3 二氧化硫排放量最小为:

(14)

式中:αi,βi,γi——第i个发电机组的碳排放系数.

3.2 约束条件

风电和电动汽车调度入网后应满足与系统机组以下约束条件.

(1) 负荷平衡为:

(15)

式中:pevg(t),pevd(t)——电动汽车t时刻充电和放电功率;

L(t)——t时刻系统的有功损耗(本文不计).

(2) 火电机组约束,包括火电机组的上下限约束、火电机组的爬坡约束、火电机组的最小允许开停机时间约束、火电机组的旋转备用约束.即:

(16)

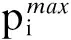
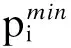
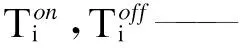
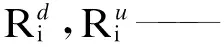
(3)风电场的出力约束为:

(17)

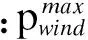
3.3 求解策略

本文采用改进粒子群算法[15],通过改进ω权重,寻求粒子最优局部解和全局解,引导粒子避开局部最差解和全局最差解,以提高寻优效率.其更新过程为:

(18)

式中:c1——粒子飞向自身最优位置的加速度系数;

c2——粒子飞向全局最优位置的加速度系数;

c3——粒子飞离自身最差位置的加速度系数;

c4——粒子飞离全局最差位置的加速度系数;

r1,r2,r3,r4——[0,l]间随机数.

平衡算法的全局搜索能力与局部寻优能力,将ω设为线性递减权重,即:

(19)

式中:ωmax,ωmin——ω的最大和最小值;T——迭代次数;Tmax——最大迭代次数.

4 算例分析

通过某风电场与10台火电机组来验证本模型的有效性.设可入网参与调度的电动汽车数量为50 000辆.风力发电厂120台同型号机组正常运行,详细参数值见文献[16],额定有功功率为240 MW.火电机组参数以及1天内各个时刻负荷预测值见文献[17].1天内风电场各个时刻输出功率曲线如图3所示.

4.1 结果分析

在不考虑风电入网情况下,电动汽车在不同V2G模式下入网前后的净负荷曲线如图4所示.由图4可知,不同充电模式下的净负荷曲线的波动性有很大区别.

表2为电动汽车不同V2G方式下的波动性比较.由表2可知,无序V2G运行模式下,充放电时刻由车主出行习惯决定,在用电高峰期充电拉大了峰谷差,增加了负荷曲线的波动;有序V2G运行模式下,峰谷差、负荷曲线波动最小.负荷高峰期,电动汽车向电网放电,减轻了火电机组的发电负担;在负荷低谷时,风力发电过于富裕,电动汽车调度入网充电,不仅消纳了过剩的风电,而且还能作为负荷高峰期的备用电源.

图3 各时刻风电厂输出功率

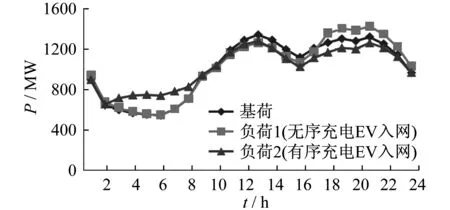
图4 不同V2G模式下的净负荷曲线

运行方式峰谷差/MW负荷方差/MW2原始负荷802.5083280.19无序充电入网883.7887561.74有序充电入网627.5840296.10

为了验证本模型的有效性,对3种不同运行方式进行比较.运行方式1为仅考虑风电并网,电动汽车不入网;运行方式2为风电并网,电动汽车无序V2G模式入网参与调度;运行方式3为风电并网,电动汽车有序V2G模式入网参与调度.不同运行方式下的负荷曲线如图5所示.由图5可知,原始负荷在没有电动汽车参与调度的情况下,峰谷差较大(802.5 MW).采用运行方式1时,仅考虑风电入网、不考虑电动汽车参与调度的情况下,虽然风电入网平均负净荷减小,但风电具有反调峰性,拉大了峰谷差(898.2 MW),增加了机组的发电负担.采用运行方式2时,电动汽车无序V2G模式与风电协调入网,因为车主的出行习惯有一定的波动性与随机性,增加了负荷曲线的波动,峰谷差较大(887.401 MW).采用运行方式3时,电动汽车有序V2G模式与风电协调入网,车主响应峰谷效应,在负荷低谷时刻充电,高峰时刻放电,削峰填谷作用明显,其峰谷差(712.58 MW)及负荷曲线波动程度最小.

图5 不同运行方式下的负荷曲线

表3为采用Matlab对3种不同运行方式下优化目标的仿真结果对比.采用运行方式1时,由于风力发电的反调峰性,增加了峰谷差,导致机组的启停次数增加,提高了机组的运行成本;采用运行方式2时,由于车主的出行习惯使峰谷差较大,负荷波动最大,增加了机组的运行成本、启停成本和SO2排放量;采用运行方式3时,在负荷高峰期,电动汽车代替发电机组向电网放电,在负荷低谷期,电动汽车调度入网充电,从而减小了峰谷差和弃风问题,有效地减小了火电机组启停成本、运行成本和SO2排放量.

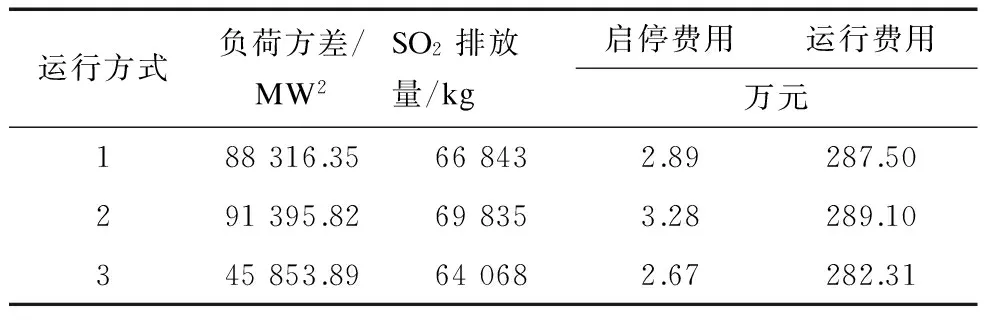
表3 优化目标比较

为了验证本文模型运行方式3的有效性.在有序V2G模式下,风电与不同数量电动汽车协调入网的净负荷曲线如图6所示.

由图6可知,有序V2G模式不仅在负荷低谷时充电增加了最低负荷,而且在电网峰值时段向系统放电,减小了负荷最大值.当50 000辆,70 000辆,100 000辆电动汽车在有序V2G模式下入网时,峰谷差分别为712.58 MW,676.57 MW,640.56 MW,由此可知有序V2G模式下电动汽车并网数量越多,其削峰填谷效果越好.

表4为最优模式下电动汽车的不同入网数量的优化结果对比.由表4可知,有序V2G模式下电动汽车入网数量越多,负荷方差越小;随着入网数量的增加,峰谷差不断降低,机组启停费用、SO2排放量不断减小.由于电动汽车入网数量不断增大,机组平均负荷随之增大,机组运行费用也会有所增加.

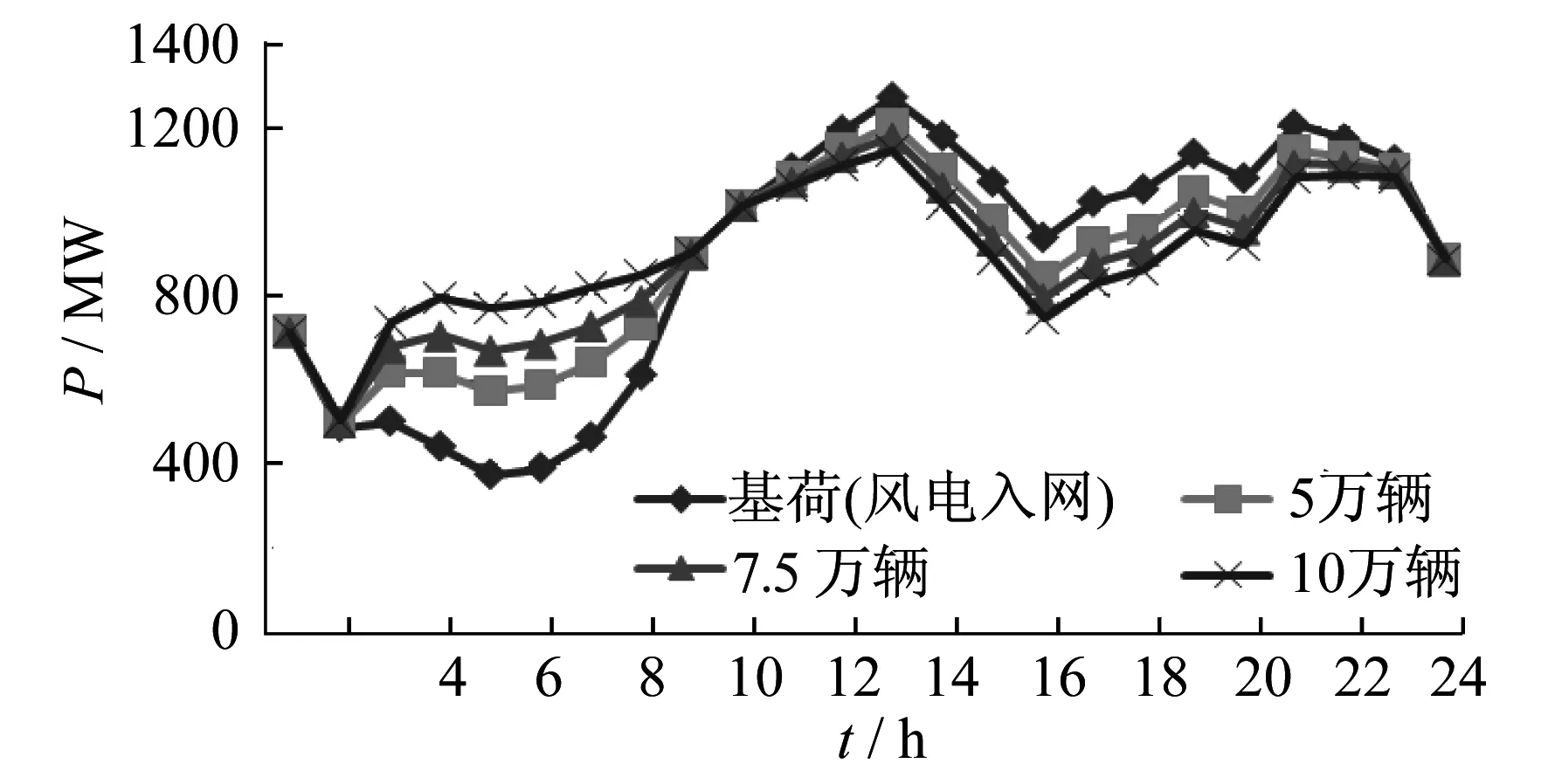
图6 风电与不同入网数量电动汽车协调入网的净负荷曲线

入网数量/万辆负荷方差/MW2SO2排放量/kg启停费用运行费用万元5.045853.89640682.67282.317.532094.21637712.08284.7910.023315.57636381.70286.64

5 结 论

(1) 电动汽车采用有序V2G运行模式时,充放电时间与风电具有时空互补性,可以发挥良好的削峰填谷作用,使电动汽车和风电联合出力更加稳定的同时,也能作为调峰电源来平缓负荷曲线的波动;

(2) 采用有序V2G模式,通过优化电动汽车充放电时间来满足风电和负荷的波动,最大程度地消纳风电,有效减小火电机组启停次数,从而减少机组启停费用和SO2排放量;

(3) 从最优入网模式下电动汽车不同入网数量比较结果可以看出,电动汽车入网数量越多,负荷方差越小,削峰填谷效果越明显,启停费用越少,环境价值越高.

[1] 陈光,戴攀,周浩,等.计及入网电动汽车和分布式电源的配电系统重构[J].电网技术,2013,37(1):82-88.

[2] 朱凌志,陈宁,韩华玲.风电消纳关键问题及应对措施分析[J].电力系统自动化,2011,35(22):29-34.

[3] 谢毓广,江晓东.储能系统对含风电的机组组合问题影响分析[J].电力系统自动化,2011,35(5):19-24.

[4] 胡泽春,宋水华,徐智威,等.电动汽车接入电网的影响与利用[J].中国电机工程学报,2012,32(4):1-10.

[5] 李惠玲,白晓民,谭闻,等.电动汽车充电对配电网的影响及对策[J].电力系统自动化,2011,35(17):38-43.[6] 鞠立伟,李欢欢,陈致宏,等.基于两步制自适应求解算法的风电-电动汽车多种并网模式效益对比分析模型[J].电网技术,2014,38(6):1 492-1 498.

[7] 蔡德福,钱斌,陈金富,等.含电动汽车充电负荷和风电的电力系统动态概率特性分析[J].电网技术,2013,37(3):590-596.

[8] 于大洋,黄海丽,雷鸣,等.电动汽车充电与风电协同调度的碳减排效益分析[J].电力系统自动化,2012,36(10):14-18.

[9] 陆凌蓉,文福拴,薛禹胜,等.计及可入网电动汽车的电力系统机组最优组合[J].电力系统自动化,2011,35(21):16-20.

[10] 侯建朝,胡群丰,周兵兵.风电与电动汽车协同并网调度多目标优化模型[J].可再生能源,2015,33(8):1 196-1 202.

[11] KANTAR Y M,Usta I.Analysis of wind speed distributions:wind distribution function derived from minimum cross entropy principles as better alternative to Weibull function[J].Energy Conversion and Management,2008,49(5):962-973.

[12] 葛少云,王龙,刘洪,等.计及电动汽车入网的峰谷电价时段优化模型研究[J].电网技术,2013,37(8):2 316-2 321.

[13] 田立亭,史双龙,贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术,2010,34(11):126-130.

[14] 施泉生,平宗飞,陈敏骏.计及电动汽车入网的电价联动模型[J].电力自动化设备,2014,34(11):34-40.

[15] 张晓辉,董兴华.含风电场多目标低碳电力系统动态经济调度研究[J].电网技术,2013,37(1):24-31.

[16] 陈海焱,陈金富,段献忠.含风电场电力系统经济调度的模糊建模及优化算法[J].电力系统自动化,2006,30(2):22-26.[17] TING T O,RAO M V C,LOO C K.A novel approach for unit commitment problem via an effective hybrid particle swarm optimization[J].IEEE Transactions on Power Systems,2006,21(1):411-418.

(编辑 胡小萍)

An Environmental and Economic Model of Grid Dispatching Coordinated with Wind Powers and Plug-in Electric Vehicles

SHI Quansheng1, DI Chao1, SUN Jiajia1, ZHANG Shenfu2, LI Shidong2

(1.SchoolofEconomicsandManagement,ShanghaiUniversityofElectricPower,Shanghai200090,China;2.StateGridTai′anPowerSupplyCompany,Tai′an271000,China)

An environmental and economic optimization model of grid dispatching coordinated with wind powers and plug-in electric vehicles is establised.Through Weibull distribution the actual wind speed is stimulated.It is concluded that through Monte Carlo simulation some electric vehicles load power under different V2G mode are obtained.Connected wind powers and electric vehicles are scheduled collaboratively to the power grid and the owners response system is scheduled to meet with the wind and load time complementarity and to reduce the load curve fluctuation in the greatest degree.The goal is the operation of the generator to minimize costs and emissions.The improved particle swarm multiple objective optimization algorithm is used to solve the model.In the Matlab environment the influence of electric vehicles at different V2G mode and plug-in grid numbers on the optimal results are analyzed and compared.

wind power; electric car; Weibull distribution; Monte Carlo simulation

10.3969/j.issn.1006-4729.2017.02.002

2016-12-19

邸超(1990-)，男，在读硕士，辽宁锦州人.主要研究方向为风电消纳与电动汽车并网的优化调度.E-mail:dichao22@.com.

“一带一路”能源电力管理与发展战略研究中心项目(WKJD15004).

TM73;TM614;U469.72

A

1006-4729(2017)02-0113-06