风力发电中LCL型单相并网逆变器的稳定性分析
曹 娜,朱春华,于 群,董 骊
(1.山东科技大学 电气与自动化工程学院,山东 青岛 266590;2.福建工程学院 信息科学与工程学院,福建 福州 350118)
风力发电中LCL型单相并网逆变器的稳定性分析
曹 娜1,朱春华1,于 群1,董 骊2
(1.山东科技大学 电气与自动化工程学院,山东 青岛 266590;2.福建工程学院 信息科学与工程学院,福建 福州 350118)
为了解决由于LCL型并网逆变器比例控制系统参数设置不当导致风力发电系统不稳定问题,以并网电流和电容电流双闭环比例控制下LCL型单相H桥并网逆变器为例,运用频闪映射方法分别建立了系统主电路和控制电路离散迭代模型,根据Jacobian矩阵特征值法分析控制参数对系统稳定性的影响并对系统稳定域进行划分。在MATLAB/Simulink中搭建系统平均模型,通过仿真获得的电流时域波形、电流-电压相位图、电流谐波谱分析图直观形象的分析验证理论分析与模型的正确性。研究结果对并网型LCL逆变器控制参数设计,避免系统不稳定现象出现具有一定的参考价值。
LCL型并网逆变器;频闪映射;离散模型;Jacobian矩阵;Simulink仿真
逆变器是目前广泛应用的一种开关器件,属于典型的非线性元器件。在一定参数下运行会出现分岔、混沌等复杂的非线性现象,影响系统稳定性。早在上世纪90年代,国内外学者开始对变换器中的非线性行为进行研究,但是主要研究对象为DC-DC变换器,少许文献对DA-AC变换器非线性行为进行研究。文献[1-2]首次研究了DC-AC变换器中的非线性行为,将非线性行为研究从DC-DC变换器延伸到DC-AC变换器,但文中参考电流是直流量,其实质仍为DC-DC变换器。文献[3-4]运用频闪映射的方法,研究了电感电流比例控制下含有L型滤波器、电阻负载的单相H桥逆变器中的分岔与混沌现象。文献[5]对电感电流PI控制方式下,含有RL负载的光伏发电系统中单相H桥逆变器的分岔现象进行了分析。文献[6]对电感电流比例控制下含有LC型滤波器、电阻负载的单相H桥逆变电路的快尺度稳定性及慢尺度稳定性进行分析。
随着新能源发电技术的发展,逆变器作为新能源并网系统的关键组成部分,其非线性特性开始被深入研究。逆变器主要通过电感型、电感电容型滤波器滤波后再并网,LCL型滤波器在高频状态下呈现高阻态,被广泛应用于大功率场合。文献[7]研究了含有LC型滤波器、并网电流控制下的光伏并网逆变器中的非线性动力学行为。文献[8]运用频闪映射的方法,通过分岔图、折叠图等仿真图,研究控制参数对含有LCL型滤波器、并网电流PI控制方式下的单相H桥逆变器稳定性的影响。文献[9]通过Jacobian矩阵方法对含有电压前馈的并网电流和电容电流双闭环比例控制方式下的的单相H桥并网逆变系统中低频振荡现象进行了分析。
目前,含有LCL型滤波器的双馈变速风电机组逆变器应用越来越广泛,LCL型逆变器的非线性行为研究较少。为了降低模型的复杂度,加快系统响应速度,本研究选择并网电流和电容电流双闭环比例控制LCL型逆变器为研究对象。通过频闪映射的方法,推导并网电流和电容电流双闭环比例控制LCL型逆变器离散迭代模型,理论计算不同比例控制参数下Jacobian矩阵对应的最大模特征值,根据最大模特征值分析控制参数对系统稳定性的影响,划分系统稳定域,最后通过MATLAB/Simulink时域仿真验证模型与理论分析的正确性。
1 LCL型并网逆变器模型建立
1.1 并网逆变器工作机理
风力发电机组并网就是通过变流器把发电机和电网联接起来,将发电机产生的电能不断地输送到系统中。变流器中逆变器的主要作用就是将直流电转换为与电网电压、频率、相位一致的交流电,实现并网。本文主要研究含有LCL型滤波器的单相全桥逆变器,其原理如图1所示。其中,E直流侧电压,S1~S4为IGBT,输出端经LCL后并入电网ug=Umsin(2πfst),其中Um为电网电压幅值,fs为电网频率,L1、L2和C构成LCL滤波器,R1和R2为电阻。
对于控制回路,采用并网电流和电容电流双闭环控制方式[10],并网电流外环用来保证并网时高功率因数,电容电流内环可以增加阻尼、抑制系统谐振。由于主要分析控制回路中比例控制参数对逆变器稳定性的影响,为了简化模型,忽略电网电压对入网电流的影响,所以采用单独比例控制方法。
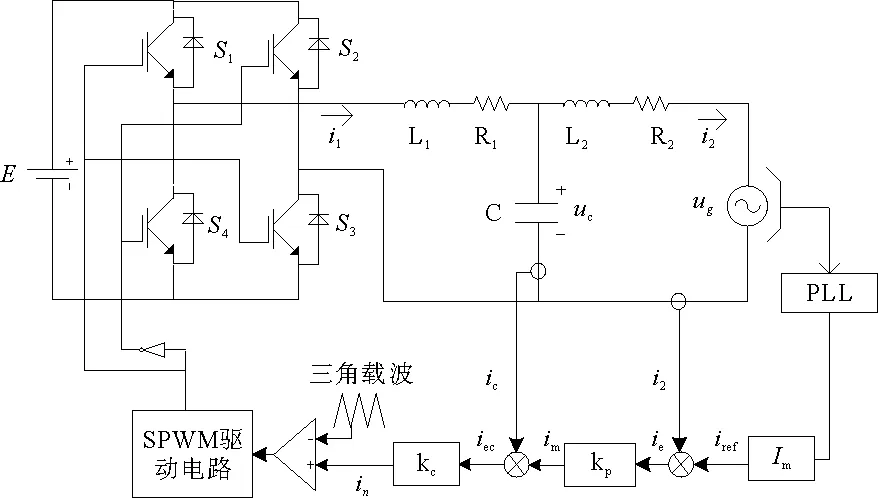
图1 LCL型并网单相全桥逆变器原理图Fig.1 Schematic diagram of single-phase grid-connected inverter with LCL filter


(1)

图2 逆变器工作状态图Fig.2 Working state diagram of inverter
图2为SPWM波产生原理,iH表示载波信号最大值,iL表示载波信号的最小值。调制信号in与三角载波信号itri进行比较,当in>itri时,输出高电平1,使S1、S3导通,S2、S4关断,系统对应状态一;当in (2) 其中,in由控制部分得到: in=[(iref-i2)kp-(i1-i2)]kc。 (3) 选择逆变器侧电流i1、并网电流i2以及电容电压uc为状态变量,在不同运行状态下,系统主电路的状态方程分别为: 状态一: (4a) 状态二: (4b) 根据IGBT工作状态,系统的工作状态可以描述为[9]: (5) 式中,S为IGBT逻辑状态。 1.2 系统离散迭代映射模型建立 对一个系统进行非线性行为分析的前提条件是要建立系统的离散化模型。运用频闪映射法推导建立LCL型并网逆变器的离散迭代模型。该方法的主要思想[8]为:以开关周期为采样的步长,在一个周期内,用周期初始时刻的状态变量表示本周期末的状态变量。 主电路状态方程(4)对应的频闪映射下的离散迭代公式如下: (6) 因此,主电路的离散方程为: (7) 根据图2可知,第n个开关周期内dn表达式如下: (8) 其中:kp、kc—电流、电压控制比例调节参数;irefn—参考电流;i1—逆变器侧输出电流;i2—并网电流。 综上所述,主电路离散迭代模型式(7)和式(8)构成了LCL型单相逆变器系统的离散模型。 与文献[8-9]相比,本研究忽略了电网电压对入网电流的影响,仅采用比例控制方法,大大简化了离散模型推导过程,提高了系统的响应速度,并且推导出的模型仅含有比例控制参数一个控制变量,针对性强。 由逆变器离散迭代模型可以看出,当直流电源E、电网电压ug、电网频率fs、L1、L2和C、R1、R2主电路组成部分参数确定后,系统稳定性将由控制系统的比例控制参数决定。不同比例控制参数下,系统Jacobian矩阵最大模特征值不同。如果最大模特征值模大于1时,则判定系统处于不稳定状态,否则判定系统稳定[11]。 特征根轨迹法是控制理论中对系统进行分析的基本方法,是一种典型的图解方法。特征根轨迹图直观形象的描述系统的特征方程的根在S平面上的分布状况,以此为依据对系统稳定性分界状态进行预测。因此,用根轨迹法分析系统的稳定性比其他方法更为方便形象。 用占空比dn替代式(5)中的S[12],就可得到系统的平均模型: (9) 根据系统平均模型求得系统的平衡点XQ=(I1Q,I2Q,UCQ)表示如下: (10) 平衡点处对应的占空比为: DQ=0.5+0.5[(iref-I2Q)kp-(I1Q-I2Q)]kc。 (11) 系统雅可比矩阵为: (12) 根据式(10)~(12)可求出系统的Jacobian矩阵的特征值,通过系统最大模特征值与1的关系来判断系统是否稳定。 选定系统参数为:E=350V,L1=2.0mH,R1=2.0Ω,L2=0.8mH,R2=0.1Ω,C=15 uF,iH=1A,iL=-1A,Im=5A,Um=311V,fs=50Hz,f=20kHz,kc=0.12。通过Matlab编程数值仿真获得kp变化时的系统根轨迹如图3,计算得出的特征值以及特征值对应的最大模值如表1所示。 图3 kp变化时系统的特征根轨迹Fig..3 Variation of system eigenvalues along with kp表1 不同kp值下对应的最大模特征值以及系统稳定性Tab.1 Variation of Jacobian matrix eigenvalues along with kp kp特征值λmax稳定性1.300-0.04520.8508±0.4937i0.9837稳定1.400-0.05350.8550±0.5128i0.9970稳定1.4230.05540.8559±0.5171i1.0000临界稳定1.425-0.05560.8560±0.5175i1.0002不稳定1.450-0.05760.8570±0.5221i1.0035不稳定1.500-0.06150.8590±0.5310i1.0098不稳定 由图3中可知,系统存在三个特征值(一个为实数,另外两个为共轭复数)。随着kp的逐渐增大,一个特征值在实轴上变化,另外两个互为共轭复数的特征值逐渐远离实轴,最后穿出单位圆。从表1中可以看出,当kp<1.423时,三个特征值其模值都小于1,判定系统稳定;当kp=1.423时,互为共轭复数的两个特征值其模值刚好为1,判定系统处于临界稳定(Hopf分岔);当kp>1.423时,互为共轭复数的两个特征值其模值大于1,判定系统不稳定。 通过上述分析,可以最大模特征值为依据对系统稳定域进行划分。kp<1.423时,系统处于稳定状态,为系统稳定域;kp>1.423时,系统首先发生Hopf分岔,然后出现发散现象,所以kp>1.423为系统不稳定区域。 通过根轨迹图对系统稳定性进行分析具有计算速度快,可以给出系统稳定域的特点,但在实际中应用还不广泛,主要原因在于该方法对模型限制较多,计算误差较大。而时域仿真方法从时域的角度对系统稳定性进行更加直观的分析,分析结果更精确,实用性和应用范围比较广,但是计算速度慢,无法给出稳定域。下面通过时域仿真来认识系统稳定性变化现象,对根轨迹法预测的系统稳定域以及模型的正确性进行验证。 在Simulink中搭建系统平均模型,通过时域仿真获得的状态变量时域波形、相位图以及谐波谱验证离散迭代模型和通过Jacobian矩阵最大模特征值法划分的稳定域的正确性。 为了仿真结果具有代表性,从运用Jacobian矩阵最大模特征值法对系统划分的稳定域、不稳定域以及稳定与不稳定的临界状态情况下各选择一个控制参数。选择对应于系统稳定、临界稳定和不稳定三个状态下的控制参数kp=1.300、kp=1.423、kp=1.500进行仿真,得电流i2波形、电流i2与电容电压uc相位图以及电流i2谐波谱如图4、5、6所示。 由图4(a)可以看出,当kp=1.300时,系统雅可比矩阵特征值最大模小于1,电流i2的时域波形为周期为0.02 s的标准正弦波,每个周期电流波形完全相同;由图4(b)可以看出,电流i2与电容电压uc相位图为单一圆环,每个周期的并网电流与电容电压完全重合,说明系统处于周期稳定状态;由图4(c)电流i2的谐波谱可以看出,电流i2中谐波分量较少,波形畸变率为0.04%,满足电能质量要求。这种状态称为系统的安全正常状态,等式约束条件和不等式约束条件都满足要求,而且系统存在一定的安全裕度。 图4 kp=1.300时仿真结果Fig.4 Simulation results when kp is 1.300 图5 kp=1.423时仿真结果Fig.5 Simulation results when kp is 1.423 由图5(a)可以看出,当kp=1.423时,系统雅可比矩阵特征值最大模等于1,电流i2的时域波形为周期为0.02 s的正弦波,但从时域图可以看出电流i2处于振荡状态,数值在稳定波形图4(a)附近上下波动;电流i2与电容电压uc相位图也不再是单一圆环,而是存在振荡现象的环形,如图5(b)所示;图5(c)电流i2的谐波谱显示此时电流i2中波形畸变率为1.64%,振荡波形频率为173 5 Hz,此时处于一种临界稳定的状态,电流波形会一直振荡下去,不衰减也不增幅。通过分析可以看出系统发生低频振荡现象时,系统发生Hopf分岔现象(雅克比矩阵特征值最大模为1)。这时系统处于临界稳定状态,虽然没有带来严重的后果,但是系统中多状态变量已越限,系统不等式约束条件不能得到满足,如果不采取有效措施,情况会进一步恶化,甚至造成严重的后果。 图6 kp=1.500时仿真结果Fig.6 Simulation results when kp is 1.500 由图6(a)可以看出,当kp=1.500时,系统雅可比矩阵特征值最大模大于1,电流i2的时域波形处于发散状态,幅值越来越大,说明控制电路不再起作用,电流i2不稳定;电流i2与电容电压uc相位图如图6(b)所示,相位图为不断向外扩散的圆形,说明电流i2与电容电压uc幅值不断扩大,系统处于不稳定状态;图6(c)电流i2的谐波谱显示此时电流i2中波形畸变率很大,波形已完全失真,系统处于崩溃状态。这种状态下,系统的等式和不等式约束条件都不满足要求,必须通过恢复状态来恢复到系统的稳定状态。实际中应该避免这种状态的出现,以免造成系统崩溃。 通过上述分析可以看出,随着比例控制参数kp的增大,系统由稳定状态过渡到临界稳定状态继而过渡成发散状态,与前文基于Jacobian矩阵特征值法分析结论相同。当系统处于发散状态时,波形畸变严重,幅值也远远超出额定值,造成电气设备损坏等严重后果。所以在逆变器参数设计时,应该尽量避免发散现象的出现。 本文模型与仿真方法能够准确分析不同比例控制参数下系统的稳定性。与文献[8]方法的比较结果如表2所示。 表2 与文献[8]方法的比较 通过上述分析可以看出,所建立的模型为并网电流和电容电流双闭环比例控制具有较好的实用性,采用单独比例控制方式,大大降低了计算量,提高计算速度。采用Jacobian矩阵最大模特征值法能准确预测系统稳定域。通过FFT对时域波形进行谐波分析,分析结果更加直观准确,更能有效地分析控制参数对系统稳定性的影响。 本研究基于频闪映射的方法推导了并网电流和电容电流双闭环比例控制LCL型逆变器的离散迭代模型。利用Jacobian矩阵特征值法分析得出比例控制参数对系统稳定性存在一定的影响,随着比例控制参数增大,系统从稳定过渡到临界稳定继而演变为不稳定状态。通过特征值根轨迹图对系统的稳定域进行预测,通过Simulink时域仿真法直观准确的验证稳定域预测的准确性和离散迭代模型的正确性,同时当系统处于临界稳定(Hopf分岔)状态时,系统发生低频振荡现象。将Jacobian矩阵特征值法和Simulink时域仿真方法相结合,更有效的对系统稳定性进行分析。研究对LCL型并网逆变器参数设计,避免系统出现不稳定现象具有一定的参考价值,为下一步三相LCL型逆变器稳定性分析奠定基础。 [1]IU H H C,ROBERT B.Control of chaos in a PWM current-mode H-bridge inverter using time-delayed feedback[J].IEEE Transactions on Circuits System I Fundamental Theory and Applications,2003,50(8):1125-1129. [2]ROBERT B,FEKI M,IU H H C.Control of a PWM inverter using proportional plus extended time-delayed feedback[J].International Journal of Bifurcation and Chaos,2006,16(1):113-128. [3]YANG P,ZHEND Q,XU Z,et al.Research on nonlinear phenomena of single-phase H-bridge inverter[C]//IEEE Pes Asia-Pacific Power and Energy Engineering Conference.IEEE,2015:1-6. [4]王学梅,张波.单相SPWM逆变器的分岔及混沌现象分析[J].电工技术学报,2009,24(1):101-107. WANG Xuemei,ZHANG Bo.Study of bifurcation and chaos in single-phase SPWM inverter[J].Transactions of China Electrotechnical Society,2009,24(1):101-107. [5]代璐,龙崦平.PI调节下光伏逆变器的分岔与混沌现象研究[J].电力系统保护与控制,2012,40(24):89-94. DAI Lu,LONG Yanping.Study of bifurcation and chaos for photovoltaic inverter with PI controller[J].Power System Protection and Control,2012,40(24):89-94. [6]周林,龙崦平,郭珂,等.基于系数线性化模型的逆变器分岔与混沌现象研究[J].电力自动化设备,2013,33(7):100-104. ZHOU Lin,LONG Yanping,GUO Ke,et al.Bifurcation and chaos of inverter system based on coefficient linear model[J].Electric Power Automation Equipment,2013,33(7):100-104. [7]廖志贤,罗晓曙,黄国现.光伏并网逆变器的非线性动力学研究[J].广西师范大学学报(自然科学版),2013,31(4):1-6. LIAO Zhixian,LUO Xiaoshu,HUANG Guoxian.Non-linear dynamics model and chaotic behavior of the single-phase full bridge photovoltaic grid-connected inverter[J].Journal of Guangxi Normal University:Natural Science Edition,2013,31(4):1-6. [8]尚佳宁,边境,李虹,等.基于频闪映射的LCL型并网逆变器的稳定性分析[J].电工技术学报,2014(增1):250-256. SHANG Jianing,BIAN Jing,LI Hong,et al.The stability analysis of grid-connected inverter with LCL filter based on the stroboscopic map[J].Transactions of China Electrotechnical Society,2014(S1):250-256. [9]周林,龙崦平,张密,等.带LCL滤波器的单相并网逆变器低频振荡现象分析[J].电力自动化设备,2014,34(1):67-71. ZHOU Lin,LONG Yanping,ZHANG Mi,et al.Analysis of low frequency oscillation in single-phase grid-connected inverter with LCL filter[J].Electric Power Automation Equipment,2014,34(1):67-71. [10]徐志英,许爱国,谢少军.采用LCL滤波器的并网逆变器双闭环入网电流控制技术[J].中国电机工程学报,2009,29(27):36-41. XU Zhiying,XU Aiguo,XIE Shaojun.Dual-loop grid current control technique for grid-connected inverter using an LCL filter[J].Proceedings of the CSEE,2009,29(27):36-41. [11]郑连清,鲁思男.Boost PFC变换器快时标分岔的控制方法[J].电力自动化设备,2013,33(10):68-73. ZHENG Lianqing,LU Sinan.Control of fast-scale bifurcation in Boost PFC converter[J].Electric Power Automation Equipment,2013,33(10):68-73. [12]彭秋波,盘宏斌,刘勇,等.LCL型三相并网逆变器双闭环解耦控制器设计[J].电工技术学报,2014,29(4):103-110. PENG Qiubo,PAN Hongbin,LIU Yong,et al.Design of dual-loop decoupling controller in LCL three-phase grid-connected inverter[J].Transactions of China Electrotechnical Society,2014,29(4):103-110. (责任编辑:李 磊) Stability Analysis of Single-phase Grid-connected Inverter with LCL Filter in Wind Power CAO Na1,ZHU Chunhua1,YU Qun1,DONG Li2 (1.College of Electrical Engineering and Automation,Shandong University of Science and Technology, Qingdao, Shandong 266590,China;2.School of Information Science and Engineering, Fujian University of Technology,Fuzhou,Fujian 350118,China) To solve the instability of wind power generation system caused by the improper control system parameter setting of grid-connected inverter with LCL filter, this paper took the single-phase H-bridge grid-connected inverter with LCL filter under grid-connected current and capacitance current control as an example and established a discrete iteration model of main circuit and control circuit by using stroboscopic map. The change of system stability along with the change of control parameters was analyzed according to the eigenvalues of Jacobian matrix and the system stability domain was divided. A system average model was established with MATLAB/Simulink ro verify the correctness of theoretical analysis and the model with the current time domain waveform, current-voltage phase diagram and current harmonic spectrum analysis chart obtained from Simulink simulation. This study can provide reference for the parameter design of grid-connected inverter with LCL filter and for the avoidance of system instability. grid-connected inverter with LCL filter;discrete model;stroboscopic map;Jacobian matrix;Simulink simulation 2016-06-24 曹娜(1971—),女,山东新泰人,博士,硕士生导师,研究方向为风力发电机系统及其控制等. E-mail:caona_2006@163.com 朱春华(1991—),女,山东昌邑人,硕士研究生,研究方向为电力系统稳定性分析,本文通信作者。E-mail:18765927118@sina.cn TN929.5 A 1672-3767(2017)03-0075-08
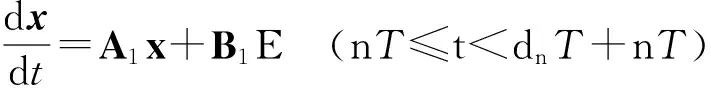
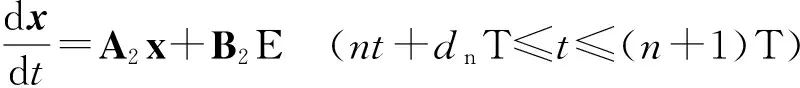






2 系统稳定性分析



3 基于平均模型的Simulink时域仿真与结果分析

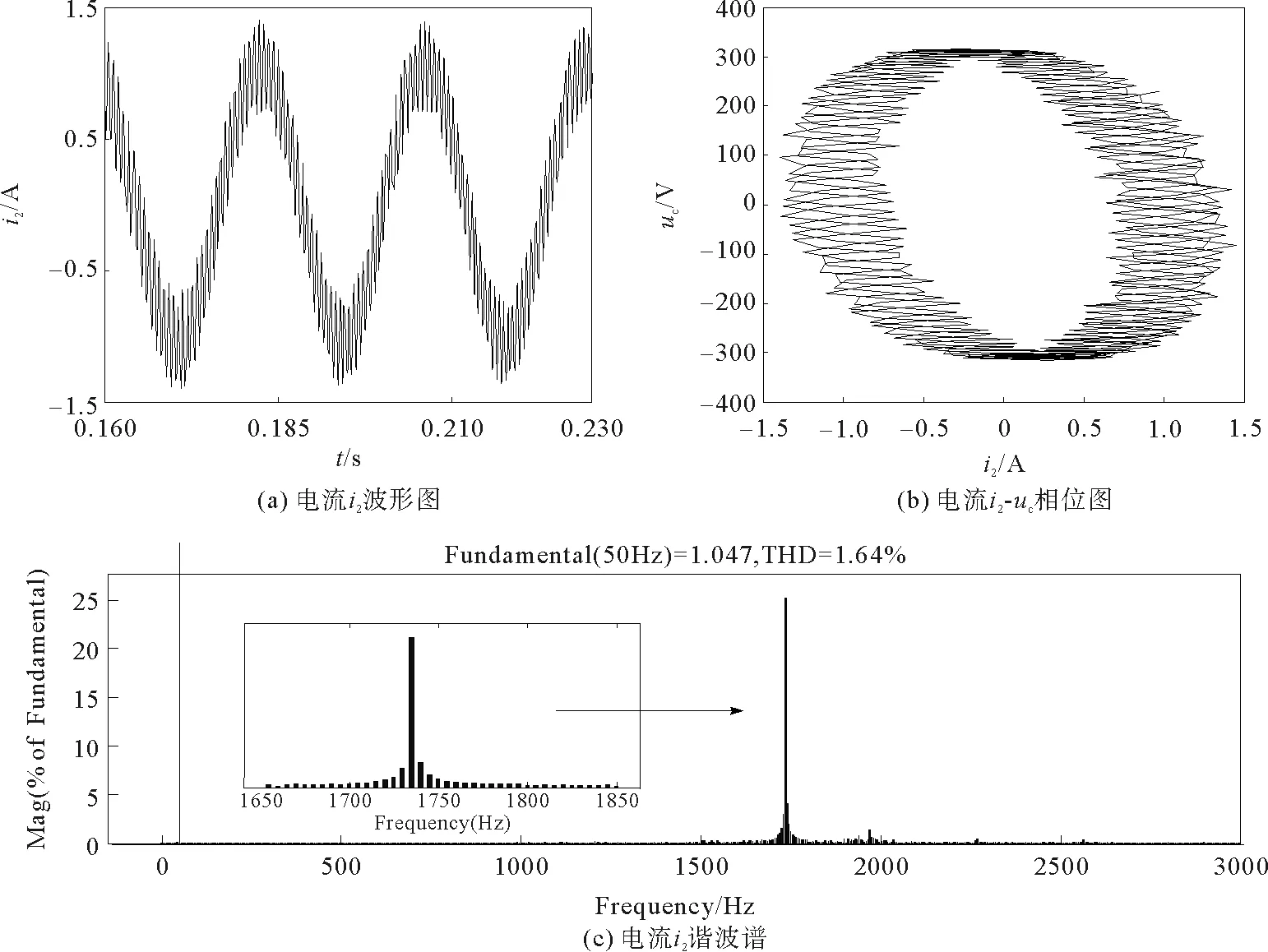


4 结论

