Mixed convection characteristics in lid-driven cavity containing heated triangular block
Krunal M.Gangawane*,B.Manikandan
Department of Chemical Engineering,University of Petroleum and Energy Studies,Dehradun 248007,Uttrakhand,India
1.Introduction
The fundamental understanding of heat transfer phenomenon is quite important as it is part of almost every other process industry.Therefore,the detailed examination of physical insights as well as the heat transfer rate in enclosures(differentially heated,lid driven,open ended,etc.,)has achieved tremendous interests from research community(due to its simple geometry and ability to illustrate varieties of fluid flow phenomenon and heat transfer behavior).Further,the details of hydrodynamic as well as thermal characteristics of heated enclosures are helpful for broad fields such as design of cooling systems of electronic gadgets,MEMS applications,high performance building insulation,multi-shed structures,furnace,food processing,lubrication technologies,solar heat collectors,and drying[1-8].Additionally,cavity/enclosure containing obstacles of varying shapes(circular,square,triangular,etc.)can be used for controlling/bifurcating/restricting the fluid flow due to convection[9,10].Though huge percentage of literature occupies the studies of mixed convection characteristics in cavity with adiabatic/isothermal obstacle of circular/square shape,very trivial is known about the effect of triangular shape on heat transfer characteristics.
On the other hand,the combined convection from heated triangular bodies/cylinders has some practical findings in process industries,such as,heat exchangers.It is well acknowledged that the square body is more bluff body than circular one,as the edges of square cylinder makes significant influence on heat transfer and fluid flow characteristics in system.Therefore,the inclined(at particular angle)edges of triangular body can significantly impact heat transfer characteristics from heated triangular cylinder/objectas compared with other cases[11,12].Furthermore,thermal conditions have remarkable effect on fluid flow and heat transfer as it controls boundary layer formation.Out of huge literature available on mixed convection from heated obstacles in cavity/enclosure,significant amount of literature have covered constant wall temperature condition.Much less is known about the effect of other important thermal conditions(linear,heat flux,etc.).Also,no information(as much known to author)is available on identification of governing parameters(Reynolds number in this case)from which convection rate deteriorate,i.e.,critical parameters.It constitutes the main objective of present work to identify such parametric range.Therefore,present numerical study is intended to analyze the mixed convection characteristics in cavity having centrally placed triangular block with either at constant wall temperature(Tw)or constant heat flux(qw)thermal condition for ranges of Prandtl,Grashof and Reynolds numbers.In particular,the effect of governing parameters(1≤Re≤1000;1≤Pr≤100;0≤Gr≤105)has been investigated for lid-driven square cavity with centered triangular block(blockage of 10%or 30%)exposed either at CWT or CHF thermal conditions.However,it is required to briefly revisit the literature on mixed convection in lid driven cavity with or without obstacle of varying shape(circular,square,triangular,etc.)to facilitate the subsequent presentment of the new simulation results.

Table 1A summary of related studies on convective flow and heat transfer from heated triangular block either in cavity(1)or channel(2)
2.Previous Work
The convection(natural+forced)characteristics in the cavities of varying configurations(viz.,differentially heated,open ended,inclined and lid driven,etc.)have been extensively explored well over the century.The excellent benchmark results for hydrodynamics in lid driven cavity are available[13-15].However,most of the available literature has explored the lid driven cavity with one of the wall heated and single or both walls moving[16-20].Indeed,very limited information of the lid driven cavity containing heated bodies for vast range of Prandtl numbers is documented.Some recent studies of mixed convection in lid driven cavities containing body or blockage are given by[21-29].Chamkha and Abu-Nada[30]numerically studied the mixed convection heat transfer in single or both lid driven cavity containing nanofluids(Al2O3).They interpreted the influence of different viscosity models.Bhattacharyaet al.[31]analyzed the multiple solutions in lid driven cavity of trapezoidal shape for mixed convection.Sivasankaranet al.[32]studied the influence of inclination angle on combined forced and natural convection heat transfer characteristics in lid driven cavity containing discrete heating source.It is observed that cavity with inclination angle of 30°yielded higher heat transfer rate.Similar study exploring the inclination angle effect is performed by Cheng and Liu[33].More recently,Abu-Nada[34]studied mixed convection in a vertical lid driven cavity with a corner heater by using dissipative particle dynamics.
On the other hand,the mixed convection study in lid driven cavity containing isothermally heated square block inside isconducted by Islametal.[35].They considered four different sizes of square blocks for range of Richardson number(0.01≤Ri≤100)at constant Reynold and Prandtl numbers of 100 and 0.71,respectively.No significant change in Nusselt number value is observed forRi≤1,after this,Nusselt number has shown rapid increase.Similar study in lid-driven cavity containing centrally placed circular cylinder is reported by Khanafer and Aithal[36].The higher heat transfer rate is observed for cavity with cylindrical body placed near bottom wall.Ray and Chatterjee[37]delineated the MHD combined convection heat transfer in lid driven cavity including heat conducting solid object of circular shape and corner heaters with Joule heating.The controlled fluid flow and heat transfer can be obtained by applying magnetic field.The influence of rotating speed of circular cylinder placed in lid driven cavity filled with nano fluid on mixed convective heat transfer analysis is explored by Chatterjeeet al.[38].More recently,Selimefendigil and Oztop[39]numerically analyzed MHD mixed convection in a nanofluid filled lid driven square cavity with a rotating circular cylinder.
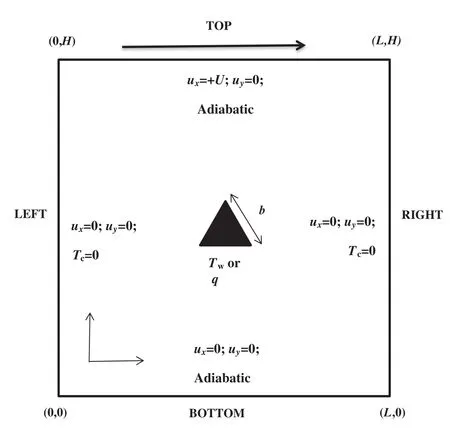
Fig.1.Physical as well as computational domain for present problem with boundary conditions.
Mixed convection from triangular prism/cylinders in channel as well as in enclosures have broad range of applications in various engineering fields such as,cooling of electronic gadgets systems and heat exchangers[40].The studies pertaining to heat transfer from heated triangular bodies have been tabulated in Table 1.It reveals from the observation of Table 1 that most studies are for channel flow with built-in triangular block[40-43]and very limited information is available on lid-driven enclosures having triangular prism/body[11,12].Mehriziet al.[44]elucidated the natural convection characteristics in horizontal cylindrical annuli with inner triangular cylinder for Cu-H20 nanofluid.They reported augmentation in heat transfer rate by positioning cylinder in downwards direction.While reverse is observed when location of inner cylinder changes horizontally.Kaltehet al.[45]studied mixed convection in lid-driven cavity containing triangular heat source placed centrally for nanofluids.They reported increase in Nusselt number values with volume fractions.Sheikholeslamiet al.[46]numerically studied natural convection of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder by using thermal lattice Boltzmann-double population method.Recently,Abdallaouiet al.[47]studied natural convection in square enclosure with decentered triangular heated body.They investigated combined influence of Rayleigh number and position of cylinder on flow and heat transfer characteristics.The flow symmetry breaks for decentered case with an improvement of the conduction behavior from cylinder to neighboring ambient wall.Some recent relevant studies exploring mixed convection in lid-driven cavities can be found elsewhere[48-53].
Therefore,in contrast to the extensive studies documented on the mixed convection in lid-driven cavities containing adiabatic/isothermal body/bodies of varying shapes(circular,square,rectangular,triangular,etc.),the lid-driven cavity containing triangular cavity in its infancy and there has been no prior study on the determination flow and thermal characteristics of the lid-driven flow regimes for wide range of Prandtl number for both limiting thermal conditions(CWT and CHF).Though few studies of enclosure with triangular body are available[40-47],all these studies have explore convection characteristics either for fixedPrnumber or nanofluids.No study(as much known to author)is available for illustrating detailed convection characteristics in square lid driven cavity with centered triangular block for thermal conditions of constant wall temperature(CWT)and constant heat flux(CHF).This literature lapse inspired us to conduct present work.Moreover,this work can be considered as extended work of authors'previous experience[12],in which triangular block is maintained at constant heat flux condition.
The present study is concerned with the elucidation of combined effect of Prandtl number(1≤Pr≤100),Reynolds number(1≤Re≤1000)and Grashof number(0≤Gr≤105)on mixed convective flow and heat transfer behavior in lid-driven square cavity containing triangular heated block for two limiting thermal conditions of CWT and CHF.The mathematical formulation part for present problem is presented in succeeding section.
3.Problem Definition,Governing Equations with Boundary Conditions

Fig.2.Streamline patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=0 and CWT.
A two dimensional,steady,laminar,mixed(forced+natural)convection heat transfer for incompressible Newtonian fluid(1≤Pr≤100)in square cavity(AR=L/H=1.0,whereLandHare crosssectional length and height of the cavity)is considered as a physical domain(Fig.1).The top wall of cavity is moving with uniform velocity(ux=Ulid)in+x-direction,while all other walls are stationary.Top and bottom walls are thermally insulated.Both vertical walls are exposed to ambient(Tc).The cavity contains equilateral triangular heated block(blockage=10%or 30%)at its center.The block is maintained either at constant wall temperature(CWT),Tw(>Tc)or constant heat flux(CHF),qw.The thermo-physical properties of the working fluid are assumed to be independent of the temperature and the viscous dissipation effects are neglected.Well known,Boussinesq approximationis commonly chosen to express dependence of density with the temperature as[11,12].Keeping in mind the limitations of the Boussinesq approximation,(ΔT)is maintained to be small such that it justifies the unaccountably of the variation of the fluid viscosity with temperature.The mass,momentum and energy equations are expressed(dimensionless form)as follows:
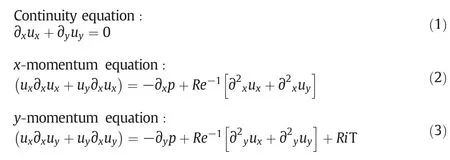
where,p,andTare Cartesian directions,velocity components,pressure and temperature,respectively.
The consistent boundary conditions for the considered configuration(Fig.1)are written as:
·West(0,y)and East(1,y)walls:These are no-slip walls and maintained at ambient isothermal temperature(Tc).
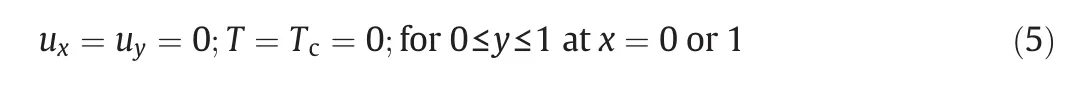
·pt?>Bottom wall(x,0):It is no-slip wall and maintained at adiabatic condition.
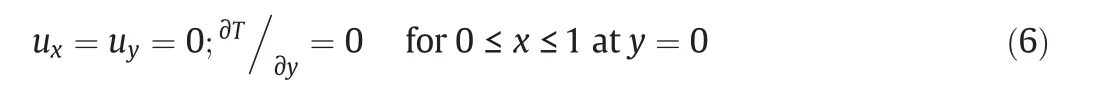
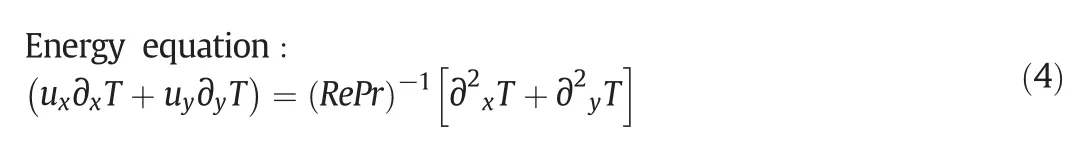
·Top wall(x,1):It is moving with uniform velocity(Ulid)and is thermally insulated.


Fig.3.Isotherm patterns fordifferent parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=0 and CWT.
·Triangular block(side,b=0.1Hor 0.3H):It is no-slip and is exposed to higher temperature and thermal conditions are expressed by means of two limiting conditions,viz.,constant wall temperature(CWT)and uniform heat flux condition(CHF).

In Eqs.(1)-(8),dimensionless variables can be obtained by using following expressions:
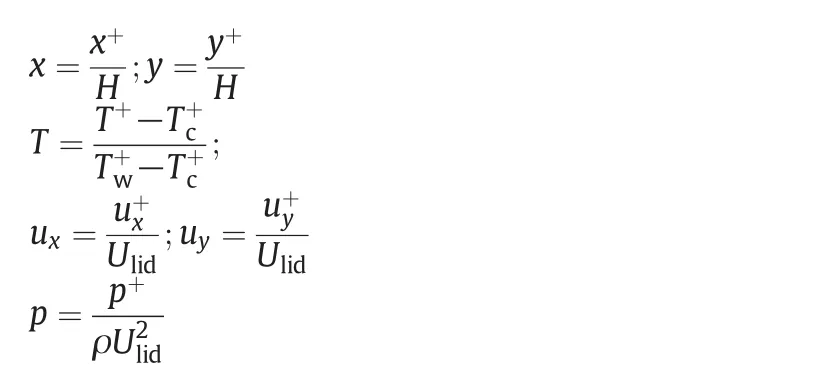
Variables with ‘+’superscripts are dimensional variables.The dimensionless groups appearing in governing equations(Eqs.(1)-(4))are represented as follows:

The solution of field equations along with the above noted boundary treatments yield the primitive variables,such asux,uy,p,andT.These field variables are further processed to obtain the engineering parameteri.e.,streamlines,vorticity,Nusselt number,etc.,in this case.These physical characteristics can be obtained as expressed below;
·Stream function(ψ):It is estimated from velocity field as,

·Estimation of Nusselt number:The local Nusselt number on the surface of the heated triangular block is estimated by the following expression[11]:
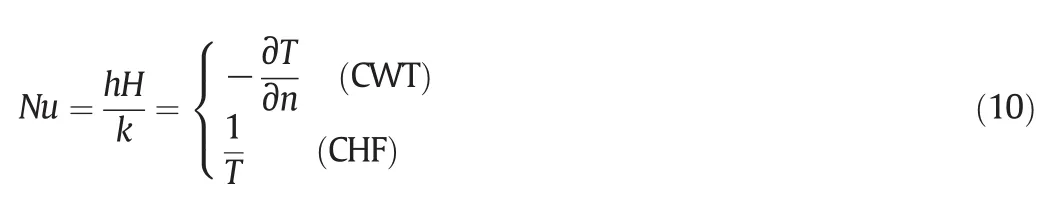

Fig.4.Streamline patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=105 and CWT.
The obtained localvalues ofNuare further averaged over the surface of a block to estimate the surface averaged Nusselt number over the triangular block.It is expressed as follows[12]:

It should be noted that average Nusselt number or dimensionless heat transfer coefficient(Nu)can be utilized in process design calculations to estimate the temperature gradient from a heated wall/object in the CWT case,or to estimate the average surface temperature over a heated wall for the CHF condition[12].
4.Numerical Methodology
Finite volume method is used to discretize the governing partial differential equations to yield a set of linear algebraic equations.The field governing equations are solved using the ANSYS FLUENT version 16.0 commercial CFD solver.The unstructured ‘triangular’cells of uniform grid spacing were generated.The well-known semi-implicit method for the pressure linked equations(SIMPLE)scheme was used to solve the pressure-velocity decoupling.The system of algebraic equations is solved by using the Gauss-Siedel(G-S)point-by-pointiterative method along with algebraic multi-grid(AMG)method which helps to reduce the number of iteration to meet desired convergence criteria.The momentum and energy terms are discretized by means of third order accurate QUICK(Quadratic Upwind Interpolation for Convection Kinetics).The iterative process is terminated for convergence criteria of 10-6forx-andy-components of velocity and 10-8for thermal field.The details of numerical methodology,grid independence test and numerical validation are already outlined in[12],therefore same has not been repeated here.Triangular mesh with 26,318 nodes and 9126 elements is found to be sufficient to resolve necessary dynamics and therefore this mesh structure is used for obtaining new results.
5.Results and Discussion

Fig.5.Isotherm patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=105 and CWT.
In this work,the mixed convection in a top lid driven square cavity is investigated numerically.In particular,the effects of inserted triangular block for different blockages,i.e.,10%and 30%on the convection characteristics have been analyzed for two limiting thermal conditions of CWT and CHF.Reynolds number is varied asRe=1,100,500 and 1000,corresponding to laminar range,Grash of number asGr=0,103,104and 105thus covering wide range of Richardson number.The Prandtl number is varied asPr=1,50 and 100(thus encompassing the fluids ranging from air to engine oil).Extensive results encompassing the influences of mentioned parameters on the local and global heat transfer characteristics(such as streamline,isotherm contours,localand average Nusselt numbers,etc.)are presented and discussed herein the ensuing section.Finally,the numerical results are also presented in the form of the predictive Nusselt number correlation.
5.1.Streamline and isotherm patterns.
Figs.2-5 illustrate the streamlines and isotherms contours for different Reynolds numbers(Re=I-1,II-100 and III-1000),Prandtl numbers(Pr=a—1,b—50 and c—100)and Grashof numbers(Gr=0 and 105)for CWT condition and blockage of 10%.Fig.2 depictthe streamline variations forGr=0(pure forced convection case)and other identical conditions ofReandPr.Analysis of Fig.2 indicates the impact of moving wall on fluid circulation in cavity.AtRe=1(signifying lower inertial forces),high velocity fluid accumulates under moving wall and above block.This high velocity fluid zone can be termed as convection cell.As fluid velocity increases(Re=100), fluid under the moving lid is found to be pulled towards the direction of lid.It shifts the convection cell towards the right top of cavity.
AtRe=1000,inertial forces are found to be significant enough to make fluid circulation throughout the cavity and triangular block oriented.The convection cell surrounds the block,indicating rigorous fluid circulation in the cavity.The impact of Prandtl number is found to be less substantial than Reynolds number.Limited influence is observed only on the size of convection cell,which slightly shrinks with augmentation inPr.Now,the temperature distribution in the cavity is depicted in Fig.4 forGr=0 and blockage of 10%for otherwise identical conditions.As it is pure forced convection case( fluid circulation due to moving wall),isotherms are found to be affected due to sliding lid.AtRe=1 and(a)Pr=1,the isotherms are distributed in parallel to vertical walls.With increase inReto 100,isotherms slightly incline in the direction of lid.As discussed,atRe=1000,due to the increase in fluid circulation strength,the isotherms are found to be distributed circularly along the block.The inclined isotherms are observed even for lower Re values forPr≥50.This behavior is observed as higherPrfluids have higher viscosity and such fluids are easily displaced due to moving lid.Also,for pure forced convection case(Gr=0),block acts as obstruction to fluid circulation in cavity.Therefore,as fluid rotates in clockwise manner,the formation of fluid plume is reported on left side of block.Due to viscous effect,the plume is found to be slightly inclined.

Fig.6.Streamline patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=0 and CHF.
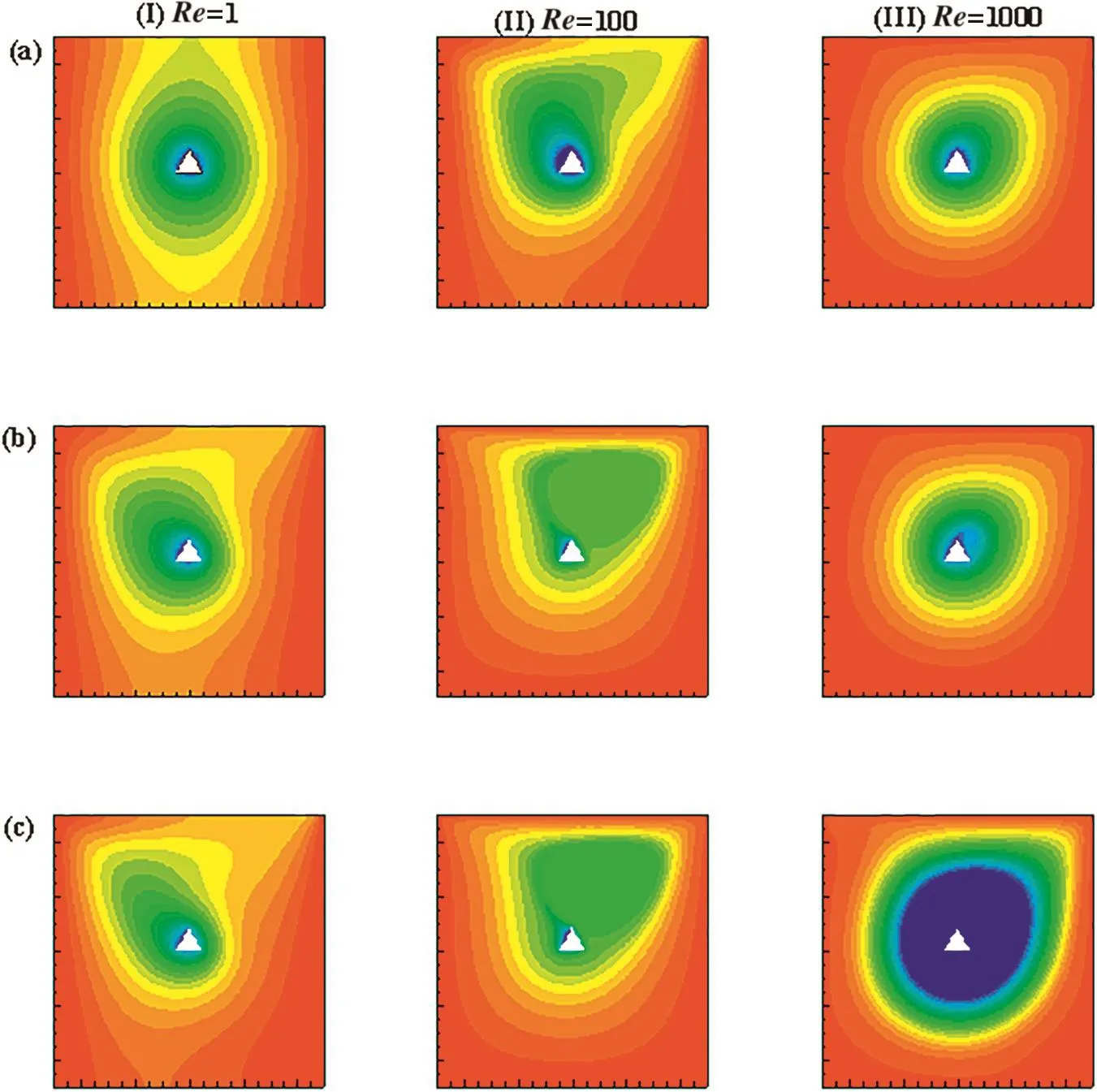
Fig.7.Isotherm patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=0 and CHF.

Fig.8.Streamline patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=105 and CHF.
Impact of natural convection dominated heat transfer is shown in Figs.4-5 for streamlines and isotherms,respectively,for CWT atGr=105.Due to dominant buoyancy force,the flow is found to be bifurcated along the vertical half of cavity.Flow circulates from heated block towards cold walls as well as due to moving lid.Therefore the regions of natural convection and forced convection can be demarcated.When flow bifurcation is observed( flow from block towards cold wall)the convection heat transfer is natural convection dominated;on the other hand,when fluid circulation occupies cavity with clockwise circulation,then it can be marked as forced convection dominant mode.The careful examination of Fig.4(streamline patterns)and from above mentioned remarks,heat transfer remains natural and forced convection dominated forRe=1 andRe=1000,respectively.This behavior is found to be true for all considered Prandtl numbers.Similarly,the isotherm profiles atGr=105are pictured in Fig.5.ForRe=1,due to dominant natural convection,isotherm lines are found to be parallel to the horizontal walls.Heat transfer is taking place from heated block towards cold vertical walls,resulting in parallel isotherms distribution to vertical walls.
For higherRe(Re=1000),due to dominant inertial forces,heated fluid circulates along with the accelerated fluid flow.Thus,isotherms are found to be distributed along the cavity in circular pattern.The increase inReandPrresults in confinement of temperature gradients along the triangular block surface,resulting in higher heat transfer rate.Further,the influence of CHF thermal condition on fluid flow and temperature distribution patterns is depicted in Figs.6-9.For pure forced convention case(Gr=0),no influence of thermal conditions is observed on streamlines(Fig.7)as well as isotherm(Fig.8)patterns.Dominant influence is observed for mixed convection dominant regions(Gr=105).Remarkable difference is observed between flow structures of CWT and CHF for similar parametric condition.AtRe=1,due to equivalent inertial and buoyancy forces,the flow bifurcation(as observed for CWT case)is not visible.Flow circulation almost occupies the cavity expect lower right zone of cavity.It is observed to be filled with low velocity fluid.The shape of this quasi-motionless region is found to be in vertical elongated form.The increase inPr,increases flow circulation and this quasi-motionless shrinks.Flow bifurcation is observed forRe≥50,but the circulation zone is situated beneath the block.Combined influence of lid and buoyancy driven flow from heated block is visible for higherPr(Pr≥50).It can be predicted that heat transfer becomes more complicated for CHF case.Subsequently,the variation of temperature inside the cavity forGr=105is shown in Fig.9.Somewhat complex dependence with physical parameters is observed as compared with CWT case.The effect ofReandPron isotherms remains same as for streamline patterns.
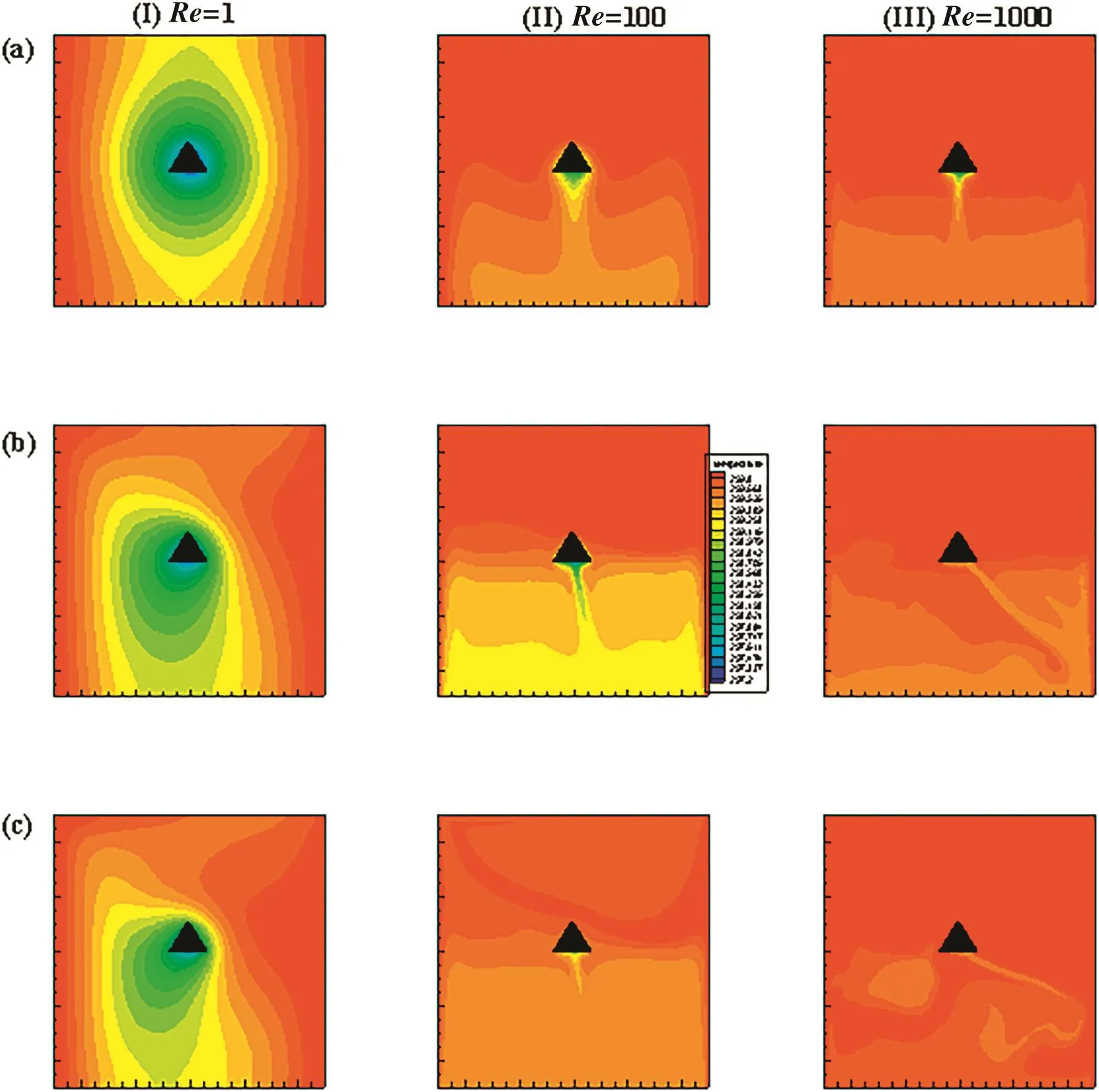
Fig.9.Isotherm patterns for different parameters(Prandtl number:(a)Pr=1,(b)Pr=50,(c)Pr=100;Reynolds number(I)Re=1,(II)Re=100 and(III)Re=1000 at Gr=105 and CHF.
All in all,it can be commented that the flow and heat transfer in cavity is more significantly affected due to Reynolds number followed byPr.Also,triangular block with CHF condition,heat transfer characteristics in cavity get more complicated.Fig.10 shows influence of larger block(blockage 30%)on streamline and isotherm patterns forGr=0 and 105.Top two rows show contours for CWT and bottom two for CHF for Reynolds number(I)Re=1,(II)Re=1000.It is evident from Fig.10 that the presence of block with blockage of 30%influence fluid flow and temperature distribution patterns only for higher Reynolds number(II-Re=1000).Streamline profiles remain more or less the same as for blockage 10%,but isotherm patterns show remarkable deviations.Isotherms are found to be distributed more confined and dense crowding as compared with CWT case,resulting in dense crowding of temperature gradients along heated wall(due to thin boundary layer thickness).Other behavior is found to be similar with the blockage of 10%.
5.2.Local as well as average Nusselt number
The Nusselt number(Nu)or local heat flux is an important physical parameter signifying the heat transfer rate in convection heat transfer studies.In convection heat transfer,the basic heat transfer parameter is heat transfer coefficient(h).The rate of heat transfer is delineated by analyzing the variation of local and average Nusselt number calculated at the heated wall for two basic limiting thermal conditions(CWT and CHF).Nusselt number is used in design calculations to estimate the rate of heat transfer from a heated wall in the CWT case,or to estimate the average surface temperature heated wall for the CHF condition.
The variation of Nusselt number value over the surface of triangular block is shown in Fig.11.Local Nusselt numbers are plotted over the triangular block surface as A→B→C→A.It is clearly evident that higherNuvalues are obtained near the edge C forGr=0(pure forced convection)and 105(natural convection dominant),respectively.ForGr=0 case,higher temperature gradients are obtained for the regions,B→C→A due to fluid motion initiated by top moving wall(this behavior is found to be true for both CWT and CHF thermal condition).As per earlier discussions, fluid drew in the direction of moving lid causing fluid flow and initiating heat transfer from heated triangular block.As known from the literature of convection studies,Reynolds number as well as Prandtl number has proportional or linear effect on Nusselt number.On contrary,higher Nusselt number values obtained forGr=105due to combined effect of heat transfer initiated due to moving lid as well as the buoyancy driven flow from heated triangular block for similar parametric conditions Out of three triangular faces,the A→B→C yielded higherNuvalues than C→A.But the difference of Nu between these surfaces is up to 40%.

Fig.10.Streamlines(I)and isotherms(II)contours for Gr=0,105 and Re=1,1000 for CWT(a,b)and CHF(c,d)thermal conditions for blockage of 30%.

Fig.12.Dependence of average Nusselt numbers with considered range of Reynolds,Prandtl and Grashof numbers as well as CWT and CHF thermal condition for blockage of10%(b=0.1).
Fig.12 delineates the variation of average Nusselt number with Reynolds number for blockage of 10%and different Grashof and Prandtl numbers.The presence of triangular body controls the convection currents for higher Reynolds numbers.AverageNuvalues show linear rise with the argumentation in Prandtl number for both thermal conditions(CWT,CHF)up toRe=80-200.After this linear sharp decrease in heat transfer rate is observed up toRe=500-1000.Thus from above discussions it can be clearly said that for present problem,Reynolds number range ofRe=80-200 can be termed as a critical Reynolds(Recr).The heat transfer augmentation is observed tillRecr,after which deterioration or no significant change is observed in heat transfer rate.The condition ofRecris valid for Grashof number up toGr=104.ForGr=105,average Nu values shows sharp decline fromRe=100 toRe=1000.It can also be noted from Fig.11 that CHF yields little bit higherNuvalues than CWT case.Thus,averageNuhas linear dependence on Grashof and Prandtl numbers;while it has complex dependence with Reynolds numbers.
The variation of averageNuwith other identical conditions for blockage of 30%is depicted in Fig.13.Similar dependence with governing parameter is visible expect for Reynolds number.As for blockage of 10%,no critical Reynolds number is identified.As the heat transfer rate due to convection is linearly proportional with heat transfer area,the increase in blockage(i.e.,size of triangular block)yields high heat transfer results.Therefore,the variation ofNuis found to be linear withRe,PrandGr.Higher heat transfer results are obtained for higher Prandtl number fluids.
5.3.Nusselt number correlation.
The empirical correlations expressing the functional dependence of the numerical/experimental results are highly appreciated due to their easy and possible use in the process engineering design and developments[5-7].In the present study,Nusselt number correlation is presented for range of flow governing considered here in(Nu=f(Re,Pr,Gr))for both thermal conditions(CWT and CHF)as well as blockage of 10%.These are expressed as follows:
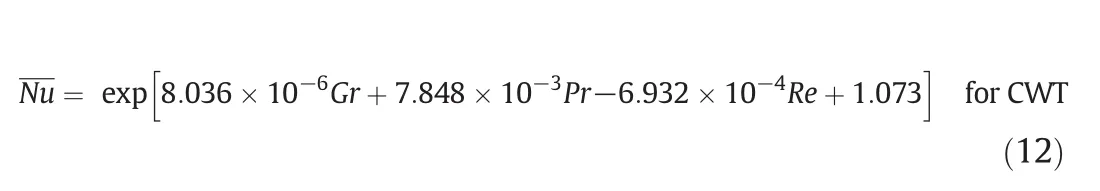
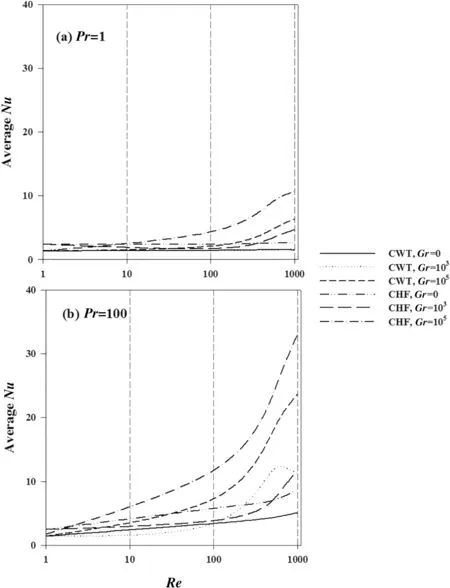
Fig.13.Dependence of average Nusselt numbers with range of Reynolds,Prandtl and Grashof numbers as well as CWT and CHF thermal condition for blockage of 30%(b=0.3H).
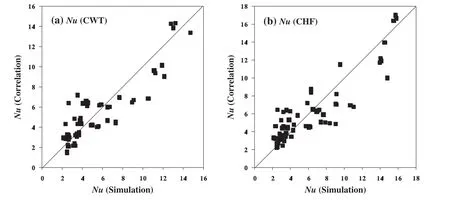
Fig.14.Comparison between simulated and predicted(by using correlations)values of average Nusselt number for blockage of 10%.
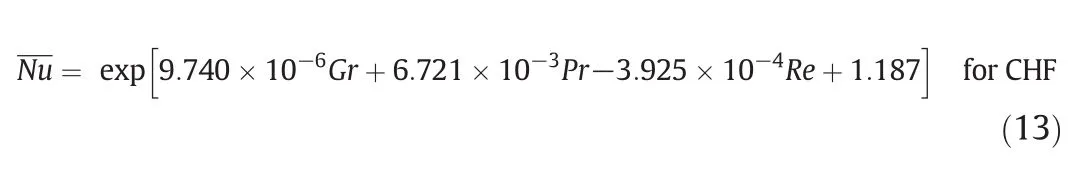
The correlation coefficients(R2)values of Eqs.(12)and(13)are estimated to be 0.856%and 0.903%,respectively.Fig.14 shows parity plot ofNuobtained by simulation and correlation(Eqs.(13)or(14)).It can be seen that the correlation shows medium likeness with simulatedNuvalues.The reason for this is we aimed to provide a single correlation for the entire range of parameters considered and due to changing phenomenon from natural to forced convection feasibility of these parameters changes.
Additionally,in order to provide best possible fit,correlations have been developed for each Grashof number separately by using the following form which is generally used in heat transfer studies.

TheNucorrelations obtained for different Grashof numbers for CWT and CHF conditions are given in Table 2 along with itsR2values.The neat observation of the Table 2 suggests that the significant effect is observed on the exponents ofReandPr.For any givenGr,Nusselt number is found to be affected more due toPrthanRe.The comparison between average Nusselt numbers obtained by present simulation with that of Table 2 correlations is shown in Fig.14.The extent of agreement between simulated and correlation seems to be fair.Additionally,Nusselt number values obtained by correlation of CHF have shown better agreement as that of CWT condition.
6.Concluding Remarks
Numerical investigation of laminar mixed convection in top lid driven square cavity with built-in triangular heated block(withblockage of 10%and 30%)for two limiting thermal conditions of constant wall temperature(CWT)and constant heat flux(CHF)is carried out by using finite volume solver.Mixed convection characteristics are analyzed for wide range of pertinent flow governing parameters such as,Reynolds number(1≤Re≤1000),Prandtl number(1≤Pr≤100)and Grashof number(0≤Gr≤105).The numerical validation of present work with literature has shown excellent agreement.It is observed that for pure forced convection case,the fluid flow caused by moving lid forms a quasi-motionless zone(convection cell)above triangular heated block.The rise in flow intensity parameter(Reynolds number)causes this cell to be shifted towards the top right corner of cavity.In case of natural convection dominated cases(Gr≥103), flow bifurcation is observed due to flow of fluid from heated triangular surfaces towards the vertical ambient wall.The increase inPrcauses crowding of isotherms towards the heated triangular block,due to increase in temperature gradient on the surface of block.The heat transfer rate shows increase only up toRe=80-200.For present problem,thus,Re=80-200 can be considered as critical Reynolds number range(Recr)for lower ofGr(0≤Gr≤103).All in all,it can be safely concluded that the insertion of triangular block can be used to control the convective flow and heat transfer in lid driven cavity.
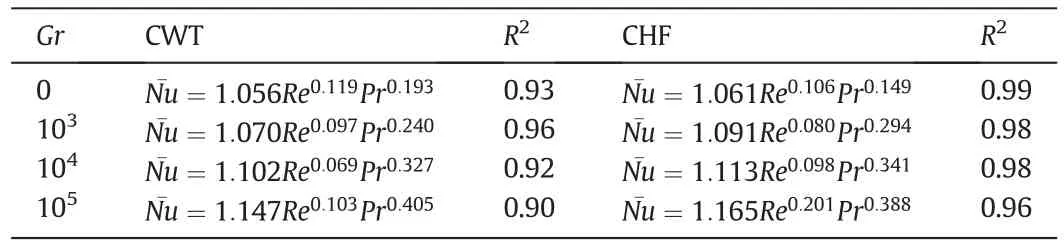
Table 2Nusselt number correlations obtained for different Grashof number for both CWT and CHF conditions
Nomenclature
ARaspect ratio,dimensionless
bsize of triangular block,m
CHF constant heat flux,W·m-2
CWT constant wall temperature,K
Cpheat capacity,J·kg-1·K-1
GrGrashof number,dimensionless
Hheight of cavity,m
hheat transfer coefficient,W·m-2·K-1
kthermal conductivity,W·m-1·K-1
Llength of cavity,m
MaMach number,dimensionless
Nulocal Nusselt number,dimensionless
Nuaverage nusselt number,dimensionless
Ppressure,N·m-2
PePeclet number,dimensionless
PrPrandtl number,dimensionless
qwheat flux,W·m-2
RaRayleigh number,dimensionless
ReReynolds number,dimensionless
RiRichardson number,dimensionless
Ttemperature,dimensionless
T* dimensional temperature,K
Tcambient temperature,dimensionless
Trefreference temperature,K
Twsurface temperature of triangular block,dimensionless
Ulidvelocity of lid,m2·s-1
ux,uyvelocity components,m2·s-1
x,yco-ordinates,m
α thermal diffusivity,m2·s-1
β coefficient of thermal expansion,K-1
ΔTtemperature difference,K
φ vorticity,m2·s-1
μ dynamic viscosity,Pa·s
ν kinematic viscosity,m2·s-1
ρ density,kg·m-3
ρ average density determined atTref,K
ψ stream function,m2·s-1
[1]S.U.S.Choi,Enhancing thermal conductivity of fluids with nanoparticles development and applications of non-Newtonian flows,pp.99-105,in:D.A.Siginer,H.P.Wang(Eds.),FED-vol.231/MD-vol.66,The American Society of Mechanical Engineers,New York,1995.
[2]J.R.Koseff,A.K.Prasad,The lid driven cavity flow:A synthesis of quantitative and qualitative observations,ASME J.Fluids Eng.106(1984)390-398.
[3]M.Morzinski,C.O.Popiel,Linear heat transfer in a two-dimensional cavity covered by a moving wall,Numer.Heat Transfer A12(1988)265-273.
[4]H.F.Oztop,Mixed convection in two-sided lid-driven differentially heated square cavity,Int.J.Heat Mass Transf.47(2004)1761-1769.
[5]K.M.Gangawane,R.P.Bharti,S.Kumar,Lattice Boltzmann analysis of natural convection in a partially heated open ended enclosure for different fluids,J.Taiwan Inst.Chem.Eng.49(2015)27-39.
[6]K.M.Gangawane,R.P.Bharti,S.Kumar,Lattice Boltzmann analysis of effect of heating location and Rayleigh number on natural convection in partially heated open ended cavity,Korean J.Chem.Eng.32(8)(2015)1498-1514.
[7]K.M.Gangawane,R.P.Bharti,S.Kumar,Two-dimensional lattice Boltzmann simulation of natural convection in differentially heated square cavity:Effect of Prandtl and Rayleigh numbers,Can.J.Chem.Eng.93(2015)766-780.
[8]S.K.Dadzie,C.Christou,Bi-velocity gas dynamics of a micro lid-driven cavity heat transfer subject to forced convection,Int.Commun.Heat Mass Transfer78(2016)175-181.
[9]M.Jami,A.Mezrhab,M.Bouzidi,P.Lallemand,Lattice Boltzmann method applied to the laminar natural convection in an enclosure with heat cylinder conducting body,Int.J.Therm.Sci.46(2007)38-47.
[10]D.Angeli,P.Levoni,G.S.Barozzi,Numerical predictions for stable buoyant regimes within a square cavity containing a heated horizontal cylinder,Int.J.Heat Mass Transf.51(2008)553-565.
[11]Krunal M.Gangawane,B.Manikandan,Laminar Natural Convection Characteristics in an Enclosure With Heated Hexagonal Block for Non-Newtonian Power Law Fluids,2016.http://dx.doi.org/10.1016/j.cjche.2016.08.028.
[12]K.M.Gangawane,Computational analysis of mixed convection heat transfer characteristics in lid-driven cavity containing triangular block with constant heat flux:Effect of Prandtl and Grashof numbers,Int.J.Heat Mass Transf.105(2017)34-57.
[13]U.Ghia,K.N.Ghia,C.T.Shin,High-resolutions for incompressible flow using the Navier-Stokes equations and a multigrid method,J.Comput.Phys.48(1982)387-411.
[14]D.Mansutti,G.Graziani,R.Piva,A discrete vector potential model for unsteady incompressible viscous flows,J.Comput.Phys.92(1991)161-184.
[15]P.N.Shankar,M.D.Deshpande,Fluid mechanics in the driven cavity,Annu.Rev.Fluid Mech.136(2000)93-136.
[16]A.K.Prasad,J.R.Koseff,Combined forced and natural convection heat transfer in a deep lid-driven cavity flow,Int.J.Heat Fluid Flow17(1996)460-467.
[17]J.Y.Oh,M.Y.Ha,K.C.Kim,Numerical study of heat transfer and flow of natural convection in an enclosure with a heat generating conducting body,Numer.Heat Transfer A31(1997)289-303.
[18]K.Khanafer,A.J.Chamkha,Mixed convection flow in lid driven enclosure filled with a fluid-saturated porous medium,Int.J.Heat Mass Transf.42(1999)2465-2481.
[19]A.M.Al-Amiri,Analysis of momentum and energy transfer in a lid-driven cavity filled with a porous medium,Int.J.Heat Mass Transf.43(2000)3513-3527.
[20]S.Roy,T.Basak,Finite element analysis of natural convection flows in a square cavity with non-uniformly heated wall(s),Int.J.Eng.Sci.43(2005)668-680.
[21]E.J.Braga,J.S.Marcelo,de Lemos,Laminar natural convection in cavities filled with circular and square rods,Int.J.Heat Mass Transf.2(2005)1289-1297.
[22]J.R.Lee,M.Y.Ha,Numerical simulation of natural convection in a horizontal enclosure with a heat-generating conducting body,Int.J.Heat Fluid Flow49(2006)2684-2702.
[23]H.F.Oztop,Z.Zhao,B.Yu,Fluid flow due to combined convection in lid-driven enclosure having a circular body,Int.J.Heat Fluid Flow30(2009)886-901.
[24]Zi-Tao Yu,Li-Wu Fan,Ya-Cai Hu,Ke-Fa Cen,Prandtl number dependence of laminar natural convection heat transfer in a horizontal cylindrical enclosure with an inner coaxial triangular cylinder,Int.J.Heat Fluid Flow53(7-8)(2010)1333-1340.
[25]T.S.Cheng,Characteristics of mixed convection heat transfer in a lid-driven square cavity with various Richardson and Prandtl numbers,Int.J.Therm.Sci.50(2011)197-205.
[26]R.Nasrin,Mixed magneto-convection in a lid-driven cavity with a sinusoidal wavy wall and a central heat conducting body,J.Nav.Archit.Mar.Eng.8(1)(2011)13-24.
[27]Y.G.Park,H.S.Yoon,M.Y.Ha,Natural convection in square enclosure with hot and cold cylinders at different vertical locations,Int.J.Heat Mass Transf.55(25-26)(2012)7911-7925.
[28]J.R.Lee,I.S.Park,Numerical analysis for Prandtl number dependency on natural convection in an enclosure having a vertical thermal gradient with a square insulator inside,Nucl.Eng.Technol.44(3)(2012)283-286.
[29]S.Parvin,M.A.Alim,N.F.Hossain,Prandtl number effect on cooling performance of a heated cylinder in an enclosure filled with nanofluid,Int.J.Heat Mass Transf.39(2012)1220-1225.
[30]A.J.Chamkha,E.Abu-Nada,Mixed convection flow in single-and double-lid driven square cavities filled with water-Al2O3nanofluid:Effect of viscosity models,Eur.J.Mech.B Fluids36(2012)82-96.
[31]M.Bhattacharya,T.Basak,H.F.Oztop,Y.Varol,Mixed convection and role of multiple solutions in lid-driven trapezoidal enclosures,Int.J.Heat Mass Transf.63(2013)366-388.
[32]S.Sivasankaran,V.Sivakumar,A.K.Hussein,Numerical study on mixed convection in an inclined lid-driven cavity with discrete heating,Int.J.Heat Mass Transf.46(2013)112-125.
[33]T.S.Cheng,W.H.Liu,Effects of cavity inclination on mixed convection heat transfer in lid-driven cavity flows,Comput.Fluids100(2014)108-122.
[34]E.Abu-Nada,Dissipative particle dynamics simulation of combined convection in a vertical lid driven cavity with a corner heater,Comput.Fluids100(2014)108-122.
[35]A.W.Islam,M.A.R.Sharif,E.S.Carlson,Mixed convection in a lid driven square cavity with an isothermally heated square blockage inside,Int.J.Heat Mass Transf.55(2012)5244-5255.
[36]K.Khanafer,S.M.Aithal,Laminar mixed convection flow and heat transfer characteristics in a lid driven cavity with a circular cylinder,Int.J.Heat Mass Transf.66(2013)200-209.
[37]S.Ray,D.Chatterjee,MHD mixed convection in a lid-driven cavity including heat conducting circular solid object and corner heaters with joule heating,Int.J.Heat Mass Transf.57(2014)200-207.
[38]D.Chatterjee,S.K.Gupta,B.Mondal,Mixed convective transport in a lid-driven cavity containing a nanofluid and a rotating circular cylinder at the center,Int.J.Heat Mass Transf.56(2014)71-78.
[39]F.Selimefendigil,H.F.Oztop,Numerical study of MHD mixed convection in a nanofluid filled lid driven square enclosure with a rotating cylinder,Int.J.Heat Mass Transf.78(2014)741-754.
[40]H.Abbassi,S.Turki,S.B.Nasrallah,Numerical investigation of forced convection in a plane channel with a built-in triangular prism,Int.J.Therm.Sci.40(2001)649-658.
[41]H.Chattopadhyay,Augmentation of heat transfer in a channel using a triangular prism,Int.J.Therm.Sci.46(2007)501-505.
[42]M.Farhadi,K.Sedighi,A.M.Korayem,Effect of wall proximity on forced convection in a plane channel with a built-in triangular cylinder,Int.J.Therm.Sci.49(2010)1010-1018.
[43]A.C.Benim,H.Chattopadhyay,A.Nahavandi,Computational analysis of turbulent forced convection in a channel with a triangular prism,Int.J.Therm.Sci.50(2011)1973-1983.
[44]A.A.Mehrizi,M.Farhadi,S.Shayamehr,Natural convection flow of Cu-water nanofluid in horizontal cylindrical annuli with inner triangular cylinder using lattice Boltzmann method,Int.Commun.Heat Mass Transfer44(2013)147-156.
[45]M.Kalteh,K.Javaherdeh,T.Azarbarzin,Numerical solution of nanofluid mixed convection heat transfer in a lid-driven square cavity with triangular heat source,Powder Technol.253(2014)780-788.
[46]M.Sheikholeslami,M.Gorji-Bandpy,K.Vajravelu,Lattice Boltzmann simulation of magnetohydrodynamic natural convection heat transfer of Al2O3-water nanofluid in a horizontal cylindrical enclosure with an inner triangular cylinder,Int.J.Heat Mass Transf.80(2015)16-25.
[47]M.El Abdallaoui,M.Hasnaoui,A.Amahmid,Numerical simulation of natural convection between a decentered triangular heating cylinder and a square outer cylinder filled with a pure fluid or a nanofluid using the Lattice Boltzmann method,Powder Technol.277(2015)193-205.
[48]K.Lioua,H.F.Oztop,M.N.Borjini,K.Al-Salem,Second law analysis in a three dimensional lid-driven cavity,Int.Commun.Heat Mass Transfer38(2011)1376-1383.
[49]L.Kolsia,K.Kalidasan,A.Alghamdi,M.N.Borjini,P.R.Kanna,Natural convection and entropy generation in a cubical cavity with twin adiabatic blocks filled by aluminum oxide-water nanofluid,Numer.Heat Transfer Part A70(3)(2016)242-259.
[50]S.Mirzakhanlari,K.M.Shirvan,M.Mamourian,A.J.Chamkha,Increment of mixed convection heat transfer and decrement of drag coefficient in a lid-driven nanofluid- filled cavity with a conductive rotating circular cylinder at different horizontal locations:A sensitivity analysis,Powder Technol.305(2017)495-508.
[51]Kolsi Lioua,H.F.Oztop,A.Alghamdi,N.Abu-Hamdeh,M.N.Borjini,H.Ben Aissia,A computational work on a three dimensional analysis of natural convection and entropy generation in nano fluid filled enclosures with triangular solid insert at the corners,J.Mol.Liq.218(2016)260-274.
[52]M.Mamourian,K.M.Shirvan,I.Pop,Sensitivity analysis for MHD effects and inclination angles on natural convection heat transfer and entropy generation of Al2O3-water nanofluid in square cavity by Response Surface Methodology,Int.Commun.Heat Mass Transfer79(2016)46-57.
[53]M.Mamourian,K.M.Shirvana,R.Ellahi,A.B.Rahimi,Optimization of mixed convection heat transfer with entropy generation in a wavy surface square lid-driven cavity by means of Taguchi approach,Int.J.Heat Mass Transf.102(2016)544-554.
 Chinese Journal of Chemical Engineering2017年10期
Chinese Journal of Chemical Engineering2017年10期
- Chinese Journal of Chemical Engineering的其它文章
- Heat transfer and friction factor of Therminol liquid phase heat transfer fluid in a ribbed tube☆
- A numerical study on heat transfer enhancement and design of a heat exchanger with porous media in continuous hydrothermal flow synthesis system
- Computationalanalysis of the flow ofpseudoplastic power-law fluids in a microchannel plate
- Investigation of droplet breakup in liquid-liquid dispersions by CFDPBM simulations:The influence of the surfactant type
- Superhydrophobic modification of ceramic membranes for vacuum membrane distillation☆
- Synthesis,characterization and application of PVA/ionic liquid mixed matrix membranes for pervaporation dehydration of isopropanol
