从一道高考题谈平面向量数量积问题处理的两种常见策略

◎朱丽娟

(江苏扬州大学附属中学东部分校，江苏 扬州 225002)

从一道高考题谈平面向量数量积问题处理的两种常见策略

◎朱丽娟

(江苏扬州大学附属中学东部分校，江苏 扬州 225002)

平面向量是高中数学新课程新增内容，也是高考重点考查的知识点.在各省及全国高考中都有出现.下面就2016年江苏高考题第13题为例，谈数量积问题处理的一般策略.

高考题；平面向量数量积；策略

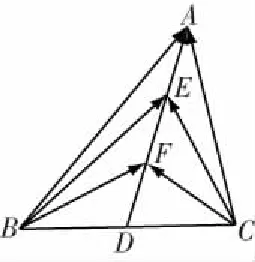
策略一：基底法

分析 平面向量基本定理告诉我们，平面中两个不共线的向量可作为一组基底，对于平面中的任意一个向量都可由这两个基底向量唯一线性表示.

一般来说，基底的选择主要有三个原则：一是已知条件中已经出现的向量；二是已知长度和角度的向量；三是表示所需向量较为容易的向量.

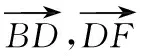
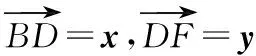
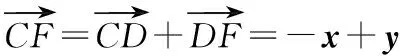
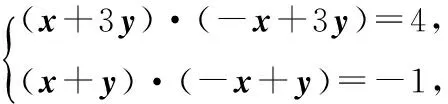
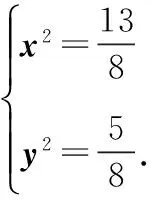
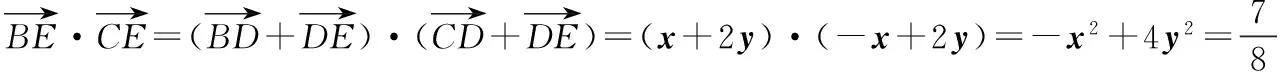
策略二：坐标法

分析 对于规则图形如直角三角形以及含直角的多边形、等腰三角形，学生易想到用建系设点的方法表示已知、未知向量，从而解决问题.但有些题目，虽然没有明显的直角或对称关系，也可以利用坐标法，设出必要参数解决问题.

本题中，条件是：在△ABC中，D是BC的中点，E，F是AD上的两个三等分点，故可以以D为坐标原点建系，设出点A的坐标，再表达出点E，F的坐标.

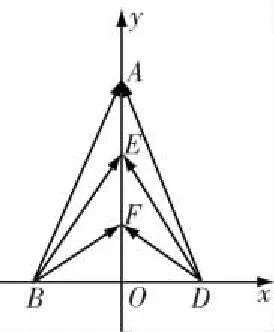
解 以D为坐标原点，BC所在直线为x轴，建立如图所示的直角坐标系.

设B(-a，0)，C(a，0)，A(3x，3y)，则E(2x，2y)，F(x，y).

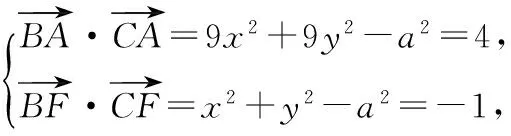
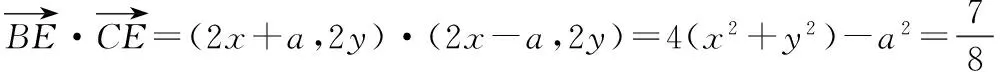
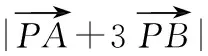
基底法和坐标法是处理平面向量数量积的两种常见策略，在很多问题求解中，这两种方式都可以方便地求出结果.学生们在具体的解题和临考发挥中，选择什么方法一击即中，需要在平时的练习中多思考和总结.