柯西不等式的向量形式及其应用

◎黄 骁

(青海师范大学，青海 西宁 810000)

柯西不等式的向量形式及其应用

◎黄 骁

(青海师范大学，青海 西宁 810000)

柯西不等式；向量；应用

构造m=(a1，a2，…，an)，n=(b1，b2，…，bn)，由于m·n=|m||n|cos〈m，n〉，而cos2〈m，n〉≤1，所以|m|2|n|2≥(m·n)2，当且仅当m∥n时，等号成立.

一、解方程组问题

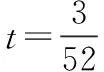
二、求最值问题

例2 已知a+2b+3c+4d+5e=30，求S=a2+2b2+3c2+4d2+5e2的最小值.

(a2+2b2+3c2+4d2+5e2)(1+2+3+4+5)≥(a+2b+3c+4d+5e)2，

三、求参数范围

例3 已知a，b，c，d，e是满足a+b+c+d+e=8且a2+b2+c2+d2+e2=16的实数，试求e的范围.

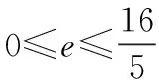
四、求代数式的值

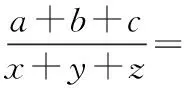
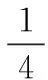
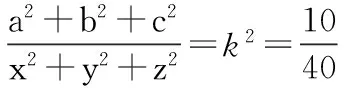
五、解决不等式问题

六、解决三角问题

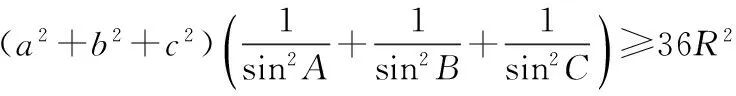
可得a2=4R2sin2A，b2=4R2sin2B，c2=4R2sin2C，

根据柯西不等式|m|2|n|2≥(m·n)2，

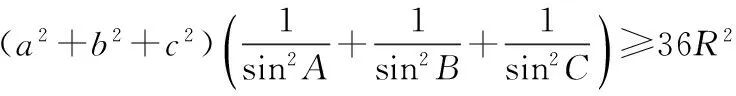
[1]余池增.柯西不等式在高中数学中的应用研究[D].广州：广州大学，2012.

[2]曹慧.柯西不等式和排序不等式在高中数学中的应用[D].西安：西北大学，2014.

[3]刘静祎.柯西不等式应用例说[J].高中数理化，2012(5)：11-12.