基于系统响应瞬时特性的非线性系统识别

秦 安 壮， 杨 志 勋， 张 明 杰， 武 文 华， 张 文 首*

( 1.大连理工大学 工程力学系, 辽宁 大连 116024；2.大连理工大学 土木工程学院, 辽宁 大连 116024 )

基于系统响应瞬时特性的非线性系统识别

秦 安 壮1， 杨 志 勋1， 张 明 杰2， 武 文 华1， 张 文 首*1

( 1.大连理工大学 工程力学系, 辽宁 大连 116024；2.大连理工大学 土木工程学院, 辽宁 大连 116024 )

在Krylov-Bogoliubov-Mitropolski(KBM)法的基础上，提出一种基于系统响应瞬时特性的非线性系统识别方法．该方法通过建立系统响应瞬时特性与系统参数之间的函数关系，从而一次性识别出所有系统参数．采用归一化Hilbert变换(normalized Hilbert transform，NHT)和广义过零(generalized zero-crossing，GZC)法求解信号瞬时振幅和瞬时频率，通过算例验证了两种方法的效果．以Duffing方程和Vanderpol方程两类非线性振动系统为例，验证了所提系统识别方法的精度．算例表明，即使在系统响应受到较大噪声污染时，该方法也有很好的识别精度．

瞬时频率；归一化Hilbert变换；广义过零法；非线性系统识别

0 引 言

工程界中普遍存在的振动系统多为非线性系统，非线性系统的参数识别一直是工程界中的热点和难点．近年来，许多学者提出了多种不同的方法，Kerschen等在文献[1]中综述了现有的方法．在现有的方法中，一种常用于弱非线性系统的方法是通过建立系统参数与系统响应瞬时特性(包括瞬时振幅和瞬时频率)之间的关系函数，从而识别出系统参数．因此，准确地计算系统响应瞬时特性对准确识别系统参数具有直接的影响．求解信号瞬时特性常用的方法有小波变换和Hilbert-Huang 变换两种，这两种方法都在非线性系统识别中得到了广泛的应用．Staszewski[2]提出了基于小波脊和小波骨架的非线性系统识别方法，并通过数值算例验证了该方法的精度．Kijewski-Correa[3]介绍了基于morlet小波变换的系统识别方法在土木工程领域的应用．Feldman[4]通过Hilbert变换获得系统响应瞬时特性的估计公式，进而识别了非线性系统的类型．Huang等[5]提出了一种改进的Hilbert变换方法，即归一化Hilbert 变换(normalized Hilbert transform，NHT)，从而更准确地计算信号的瞬时频率．Pai[6]将Hilbert-Huang变换应用到多种类型的非线性振动识别中，均取得了较好的识别精度．Feldman[4]综述了Hilbert变换在机械振动系统识别领域中的应用．

本文在Krylov-Bogoliubov-Mitropolski(KBM)法[7]的基础上，基于系统响应提出系统参数识别方法．此方法可一次性识别系统参数．将此方法应用到Duffing方程和Vanderpol方程两类非线性振动系统中，以验证在噪声干扰情况下该方法的精度．

1 基本理论

1.1 归一化Hilbert变换

非线性系统响应时程具有非平稳、非线性的特性．瞬时频率是分析非平稳、非线性信号强有力的工具．早在1946年，Gabor就提出通过Hilbert变换构造解析信号从而求瞬时频率的方法．对于任意单频率分量信号

y(t)=Q(t)cos[φ(t)]

(1)

式中：y(t)为一多分量信号；Q(t)为瞬时振幅；φ(t)=2πf0t+θ(t)为瞬时相位角．

y(t)的解析信号定义为

Y(t)=y(t)+iq[y(t)]

(2)

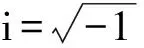
H[y(t)]=H{Q(t)cos[φ(t)]}=

Q(t)H{cos[φ(t)]}

(3)

至此，y(t)的瞬时振幅和瞬时频率分别表示为

(4)

(5)

然而，根据Bedrosian定理[8]，只有在Q(t)和cos[φ(t)]的频谱完全分离时，式(3)才能严格成立．Nuttall等[9]还指出，调幅或调频信号的Hilbert 变换并不等同于其正交分量，并给出了两者之间的整体误差：

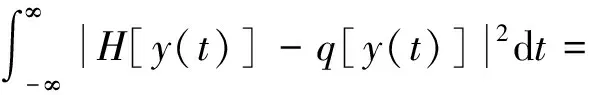
(6)

其中F(f)是Q(t)eiθ(t)的傅里叶谱．

可见，式(4)和(5)不能准确求解信号的瞬时振幅和瞬时频率．Huang提出了将单频率分量信号归一化再进行Hilbert变换的方法，如式(7)所示．

(7)

其中y1(t)是y(t)归一化得到的信号；e1(t)是y(t) 的经验包络，由y(t)的极大值点三次样条插值得到．归一化的过程往往需要重复若干次，以确保归一化后的信号幅值不超过1，即

(8)

定义y(t)的调频部分

F(t)=yn(t)=cos[φ(t)]

(9)

显然F(t)保留了所有与y(t)频率相关的信息．由于F(t)的幅值等于1，对F(t)进行Hilbert变换不再受Bedrosian定理限制．此外，Huang对F(t)与其Hilbert变换之间的误差给出了一种更为实用的表达式：

(10)

其中H[F(t)]为F(t)的Hilbert变换．

Huang把这种先归一化再进行Hilbert变换的方法称为归一化Hilbert变换(NHT)，并在文献[5]中验证了这种方法的优越性．

1.2 广义过零法

过零法是一种常用的计算信号局部频率的方法，其基本思想是根据连续过零点之间的时间间隔来确定局部频率，因为该方法计算的频率在连续过零点之间为一个定值．Huang等[5]在过零法的基础上提出将过零点和极值点视为控制点，从而将时间分辨率提高到四分之一波形，并把改进的方法命名为广义过零(generalized zero-crossing, GZC)法．Huang 将两个连续的同类型过零点或同类型极值点间的时间间隔定义为一个整周期，信号中任意一点同时属于4个整周期，定义为T4j，j=1,2,3,4；将两个连续的不同类型过零点或不同类型极值点间的时间间隔定义为一个半周期，信号中任意一点同时属于两个半周期，定义为T2j，j=1,2；将任意过零点与其相邻极值点间的时间间隔定义为一个四分之一周期，信号中任意一点只属于一个四分之一周期，定义为T1．根据三类周期的局部程度，分别赋予T1、T2j、T4j权重因子4、2、1．至此，任意点的角频率可表示为

(11)

GZC通过测量控制点间的时间间隔来计算局部频率，其物理意义非常明确[5]．此外，该方法不涉及任何形式的变换和微分，因此具有极好的鲁棒性．由于实际采样信号总是离散的，采样信号不能总是准确地采集到极值点和过零点．因此本文对上述方法进行改进：对于过零点，通过对最接近其的两个采样点线性插值得到；对于极值点，通过对最接近其的7个采样点二次抛物线拟合得到．

1.3 仿真信号分析

为验证NHT和GZC两种方法的可靠性，对以下调幅调频信号进行分析：

x(t)=e-0.15t[sin(5πt)+0.1cos(5πt)]

(12)

信号时域波形示于图1，采样频率和采样时长分别为100 Hz和15 s．由Hilbert变换求得的瞬时振幅示于图1，NHT和GZC求得的瞬时频率示于图2．为了使结果更为清晰，图2只显示了第4 s到第8 s的瞬时频率结果．可见NHT方法的结果与实际瞬时频率吻合良好，GZC方法的结果也能较好反映实际瞬时频率的趋势．

图1 振动响应

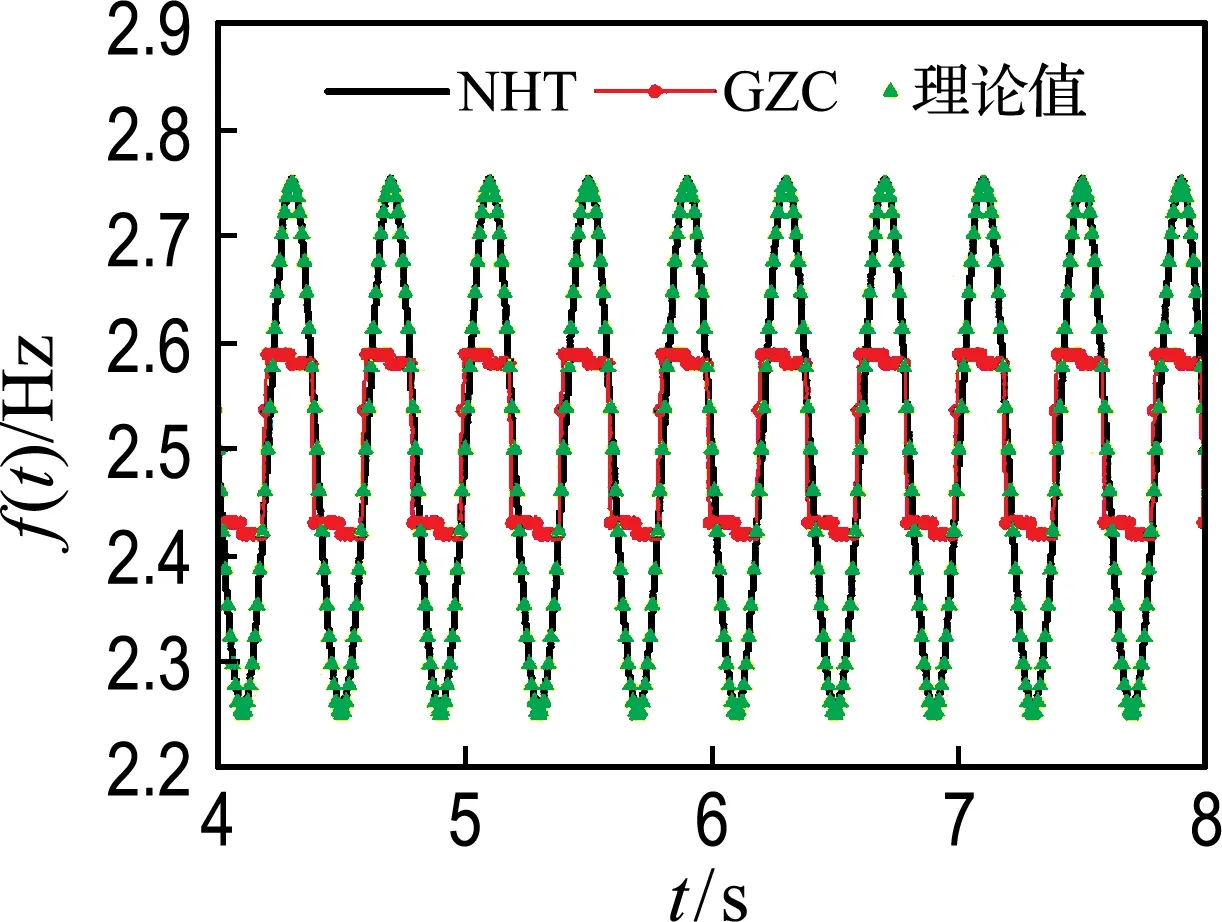
图2 原信号瞬时频率

为考察噪声对本文方法识别精度的影响，在x(t)中加入零均值白噪声，并定义噪声比例如下：

(13)

在x(t)加入5%的白噪声后，求得的瞬时频率示于图3．可见NHT方法结果出现较大波动，GZC方法结果与加入噪声前的结果基本相同，说明GZC方法抗噪性能较好．这是由于GZC方法不涉及任何形式的变换和求导，通过直接测量零点和极值点间的时间间隔获得信号的局部频率，因此抗噪性能良好[5]．

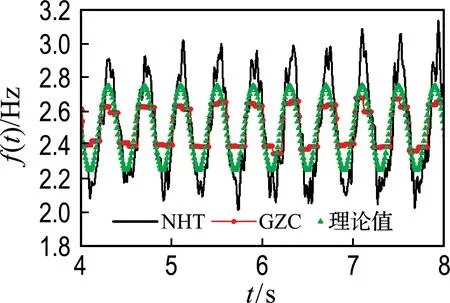
图3 噪声污染信号瞬时频率

2 方法介绍

对于单自由度弱非线性动力系统，其自由振动方程可表示为

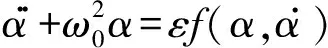
α．．+ω20α=εf(α，α．)

(14)

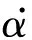
α．

和

α．．

分别是系统的位移、速度和加速度；

ω

0

是系统线性化方程的振动角频率；

ε

是小参数；

f

是关于

α

和

α．

的非线性方程．

根据KBM法，式(14)的解可近似表示为[10]

α(t)=Q(t)cos[φ(t)]

(15)

式中：Q(t)为瞬时振幅；φ(t)=ω0t+θ(t)为瞬时相位角，φ(t)对时间的一阶导数为瞬时频率；Q(t)和θ(t)均为随时间慢变的函数．

式(15)对时间求导得

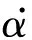
α．

(

t

)=

Q．

(

t

)cos[

φ

(

t

)]-

Q

(

t

)

θ．

(

t

)× sin[

φ

(

t

)]-

Q

(

t

)

ω

0

sin[

φ

(

t

)]

(16)

由于Q(t)和θ(t)均为随时间慢变的函数，式(16)右端前两项将远小于第3项，因此可以认为

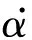
α．

(

t

)=-

Q

(

t

)

ω

0

sin[

φ

(

t

)]

(17)

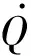
Q．

(

t

)cos[

φ

(

t

)]-

Q

(

t

)

θ．

(

t

)sin[

φ

(

t

)]=0

(18)

类似地，可以得到

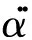
α．．

-Q(t)ω20cos[φ(t)]-Q．(t)ω0sin[φ(t)]-

(

t

)=

Q

(

t

)

ω

0

θ．

(

t

)cos[

φ

(

t

)]

(19)

将式(17)和(19)代入式(14)，得

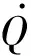
Q．

(

t

)

ω

0

sin[

φ

(

t

)]+

Q

(

t

)

ω

0

θ．

(

t

)cos[

φ

(

t

)]= -

εf

{

Q

(

t

)cos[

φ

(

t

)],-

Q

(

t

)

ω

0

sin[

φ

(

t

)]}

(20)

联立式(18)和(20)，得

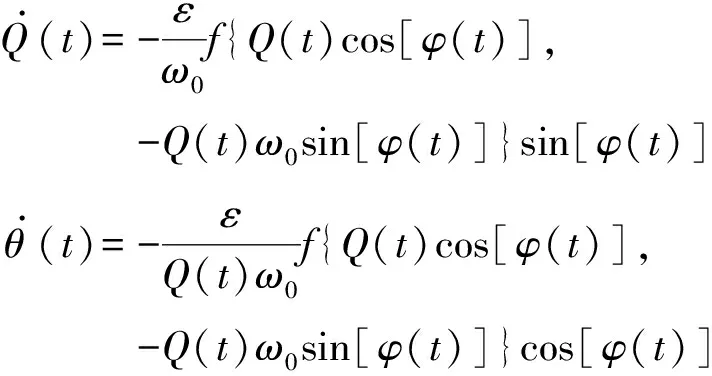
Q．(t)=-εω0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}sin[φ(t)]θ．(t)=-εQ(t)ω0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}cos[φ(t)]

(21)

Q．

(

t

)和

θ．

(

t

)在一个周期内进行平均，有

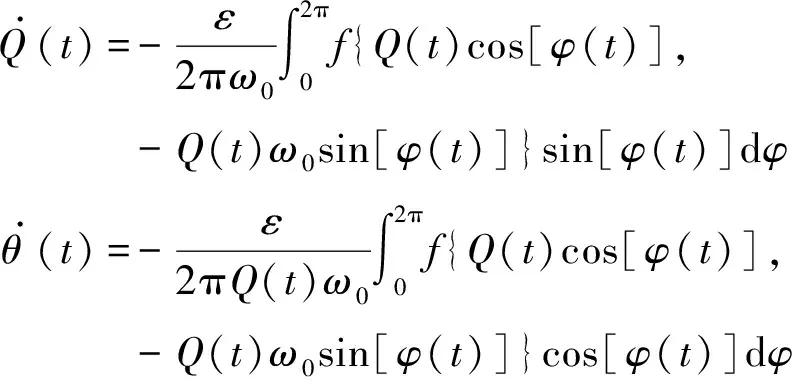
Q．(t)=-ε2πω0∫2π0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}sin[φ(t)]dφθ．(t)=-ε2πQ(t)ω0∫2π0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}cos[φ(t)]dφ

(22)

由于φ(t)=ω0t+θ(t)，从而

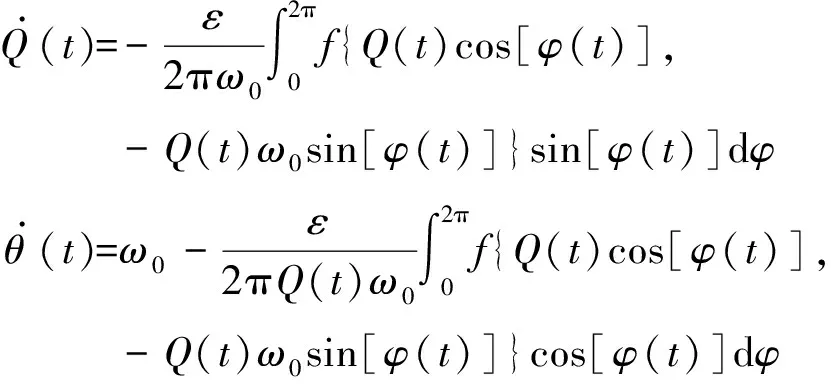
Q．(t)=-ε2πω0∫2π0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}sin[φ(t)]dφθ．(t)=ω0-ε2πQ(t)ω0∫2π0f{Q(t)cos[φ(t)]，-Q(t)ω0sin[φ(t)]}cos[φ(t)]dφ

(23)

对于一般的工程问题，可以通过适当假定非线性项的形式，代入式(23)从而建立系统响应瞬时特性与系统参数之间的函数关系．下面将通过算例进一步介绍该方法的流程．

3 数值算例

3.1 Duffing非线性振动系统

考虑下式所示的Duffing方程：

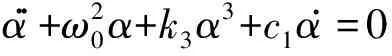
α．．+ω20α+k3α3+c1α．=0

(24)

即相当于式(14)中

(25)

将式(25)代入式(23)可得

(26)

至此，如果可以得到系统振动响应时程的瞬时振幅及瞬时频率，即可根据式(26)最小二乘拟合识别系统参数ω0、k3、c1．

作为算例，取ω0=45 rad/s，k3=10，c1=0.1，采用四阶龙格-库塔法计算其在初始振幅为5 mm，初始速度为零时的振动响应，如图4所示．

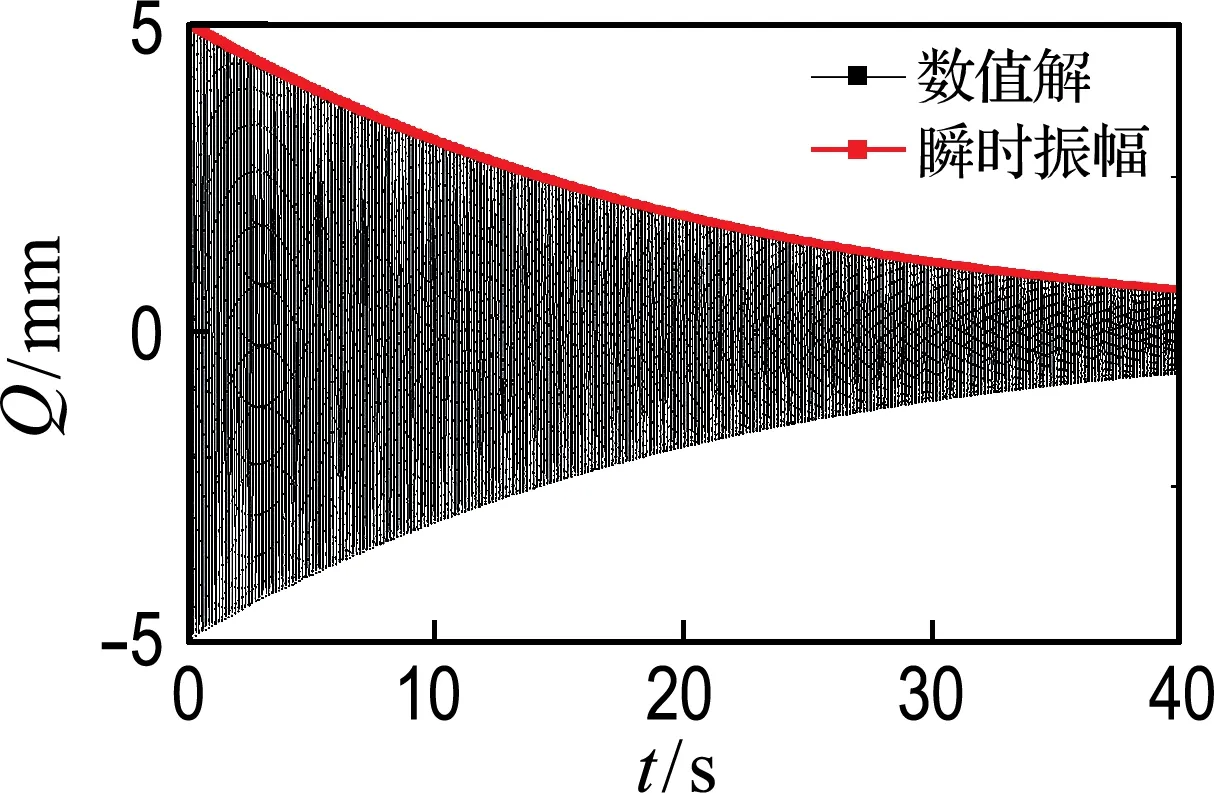
图4 Duffing非线性振动系统的振动响应

图5为该响应时程的功率谱密度，其中纵坐标是以10为底的对数坐标．可见响应包含7、21和35 Hz 3个频率带，高阶成分能量很低．根据文献[11-12]，EMD分解很难筛选出能量较低的频率成分．因此，本例将振动响应时程通过一个零相位数字滤波器[13]从而获得单频率分量信号．

通过Hilbert变换得到的瞬时振幅示于图4中，NHT和GZC方法求得的瞬时角频率示于图6中．在使用NHT方法求瞬时角频率时，信号两端分别用与其第一个和最后一个周期相同的波形延长，从而减轻端部效应．可见，两种方法求得的瞬时角频率趋势十分相似，NHT方法的结果波动更大，这与Huang在文献[5]中的结果相吻合．

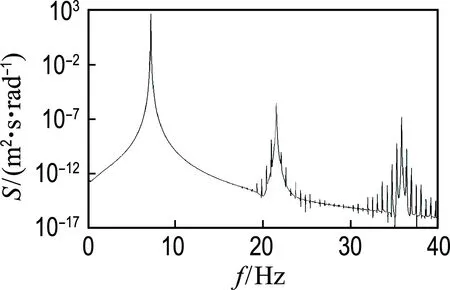
图5 Duffing非线性振动系统的功率谱密度

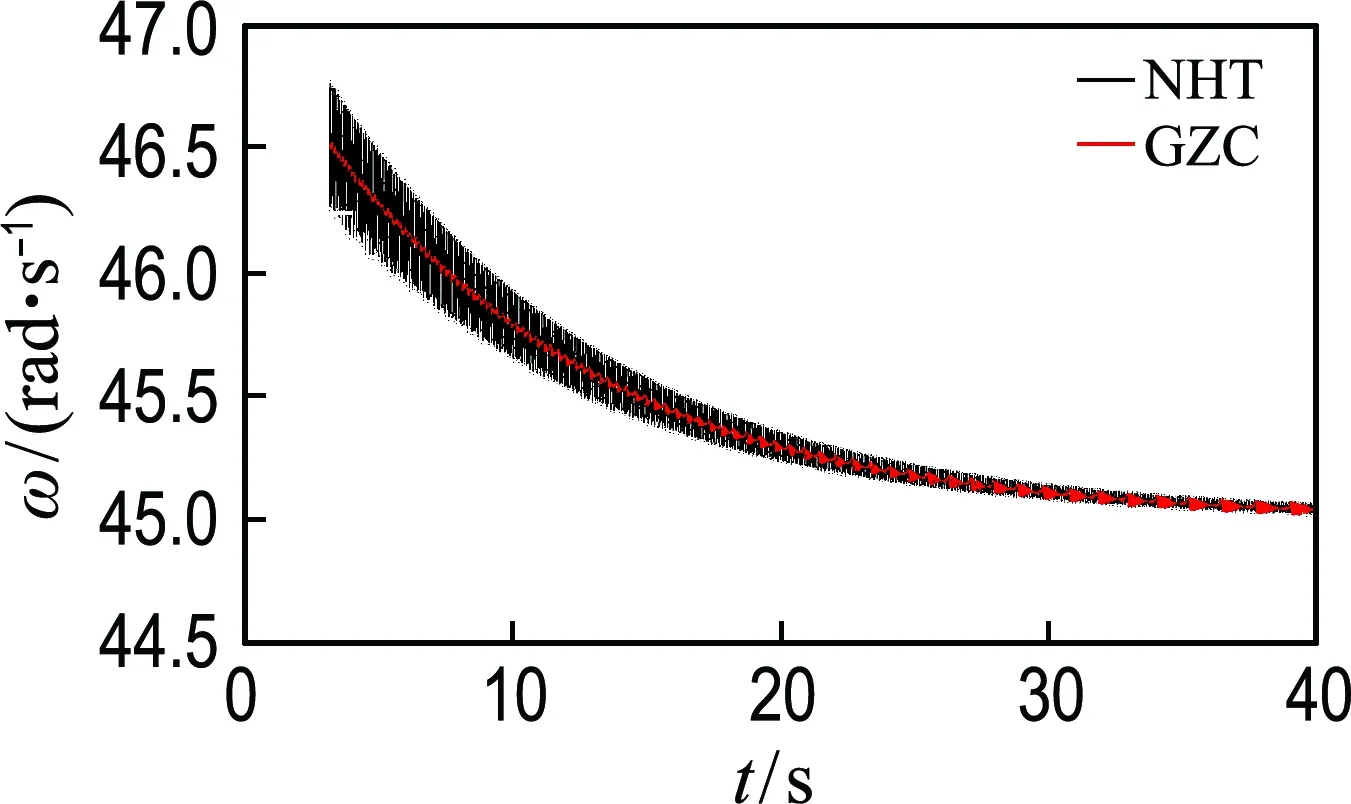
图6 Duffing非线性振动系统的瞬时角频率

将瞬时振幅和瞬时角频率结果代入式(26)，通过最小二乘拟合识别系统参数，各参数识别结果示于表1．可见各参数识别结果具有很好的精度，即使在信号受到10%噪声污染时，各参数识别结果误差都在4%以内．因此，本文方法对该类系统识别精度较高，且具有良好的抗噪性．

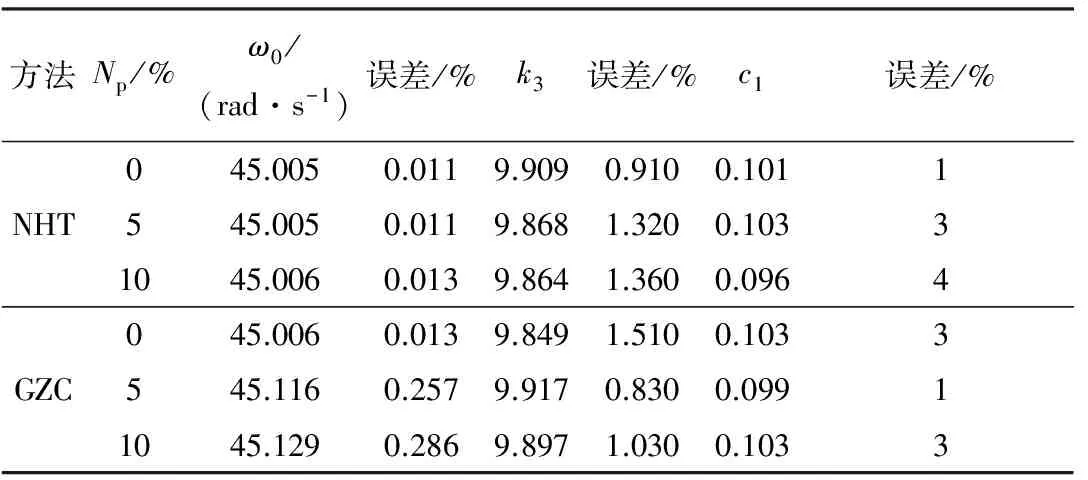
表1 Duffing非线性振动系统的识别结果

3.2 Vanderpol非线性振动系统

如下式所示的Vanderpol方程：

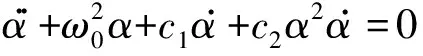
α．．+ω20α+c1α．+c2α2α．=0

(27)

即相当于式(14)中

(28)

将式(28)代入式(23)可得

(29)

至此，如果可以得到系统振动响应时程的瞬时振幅及瞬时频率，即可根据式(29)最小二乘拟合识别系统参数ω0、c1、c2．

作为算例，取ω0=45 rad/s，c1=0.1，c2=0.1，采用四阶龙格-库塔法计算其在初始振幅为5 mm，初始速度为零时的振动响应，结果如图7所示．

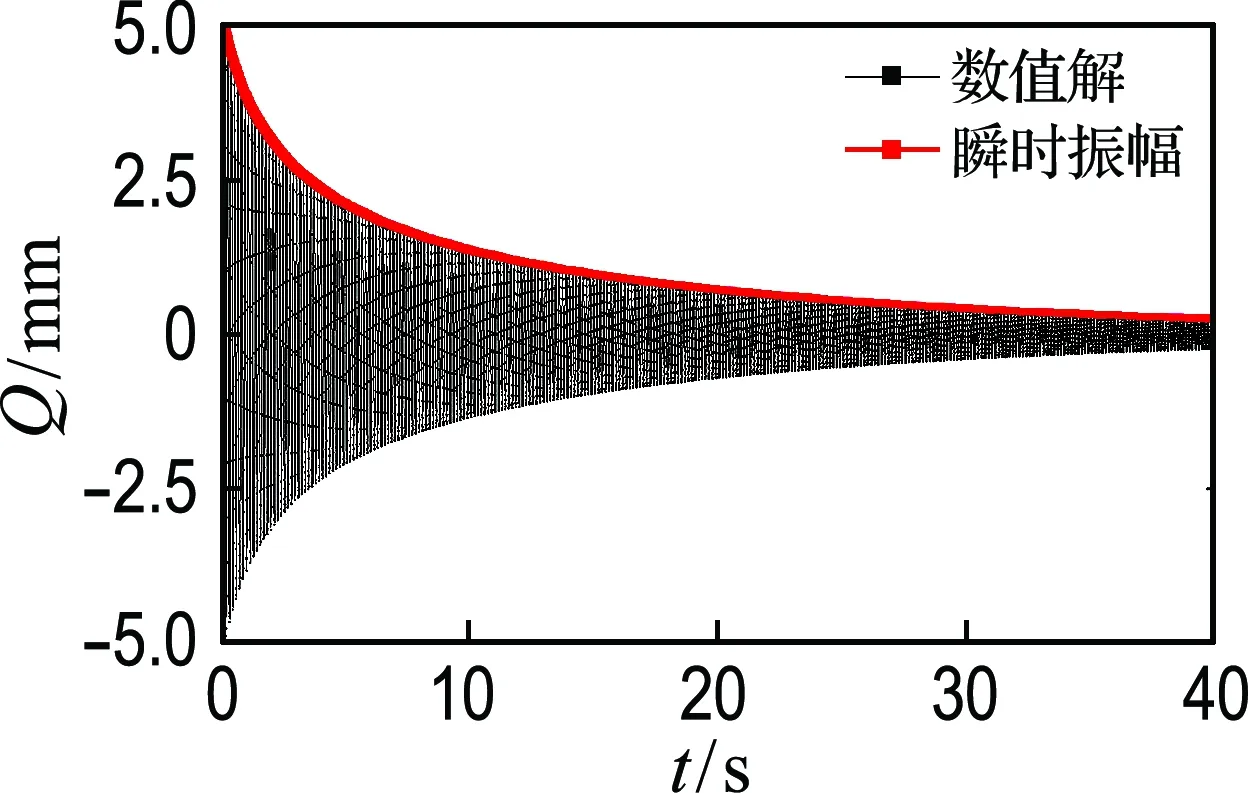
图7 Vanderpol非线性振动系统的振动响应

图8为该响应时程的功率谱密度，其中纵坐标是以10为底的对数坐标．可见响应包含7、21和35 Hz 3个频率带，高阶成分能量很低．同样，本例将振动响应时程通过一个零相位数字滤波器从而获得单频率分量信号．

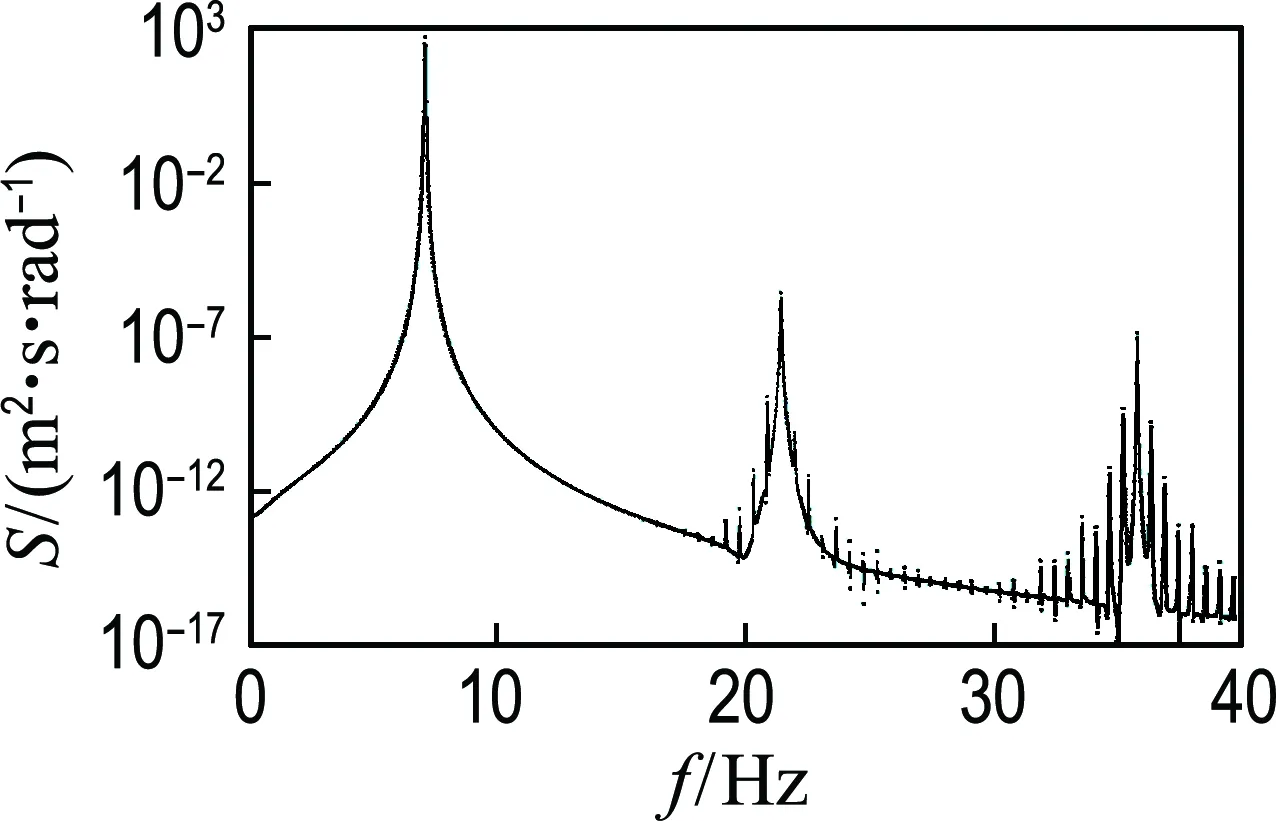
图8 Vanderpol非线性振动系统的功率谱密度

通过Hilbert变换得到的瞬时振幅示于图7中，NHT和GZC方法求得的瞬时角频率示于图9中．在使用NHT方法求瞬时角频率时，信号两端分别用与第一个和最后一个波形相同的正弦波延长，从而减轻了端部效应．可见，两种方法求得的瞬时角频率结果吻合良好．

将瞬时振幅和瞬时角频率结果代入式(29)，通过最小二乘拟合识别系统参数，各参数识别结果示于表2．可见各参数识别结果具有很好的精度，即使在信号受到10%噪声污染时，各参数识别结果误差都在3%以内．因此，本文方法对该类系统识别精度较高，且具有良好的抗噪性．

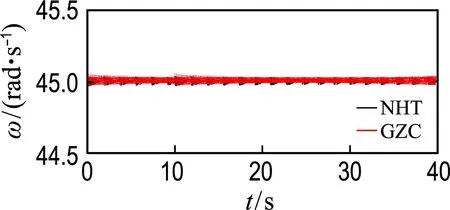
图9 Vanderpol非线性振动系统的瞬时角频率

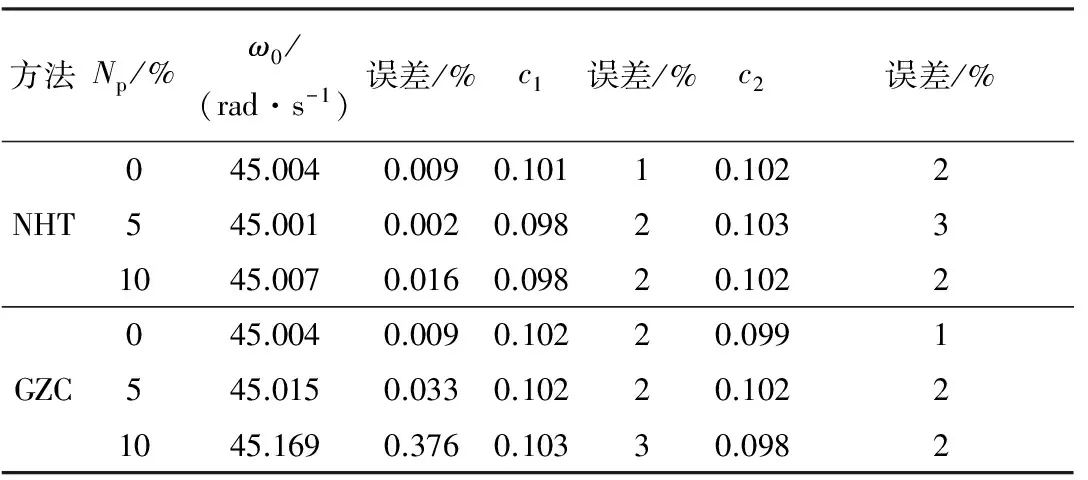
表2 Vanderpol非线性振动系统的识别结果

4 结 语

本文在KBM法的基础上，提出了一种基于系统响应瞬时特性的非线性系统识别方法；采用归一化Hilbert变换和广义过零法求解信号瞬时振幅和瞬时频率，通过算例验证了两种方法的效果；将本文提出的系统识别方法应用到Duffing方程和Vanderpol方程两类非线性振动系统，发现即使在系统响应受到较大噪声污染时，本文方法也有很好的识别精度．

[1] KERSCHEN G, GOLINVAL J C. Generation of accurate finite element models of nonlinear systems — application to an aeroplane-like structure [J]. Nonlinear Dynamics, 2005, 39(1/2):129-142.

[2] STASZEWSKI W J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform [J]. Journal of Sound and Vibration, 1998, 214(4):639-658.

[3] KIJEWSKI-CORREA T L. Full-scale measurements and system identification:A time-frequency perspective [D]. Notre Dame:University of Notre Dame, 2003.

[4] FELDMAN M. Non-linear system vibration analysis using Hilbert transform — I. Free vibration analysis method ′Freevib′ [J]. Mechanical Systems and Signal Processing, 1994, 8(2):119-127.

[5] HUANG N E, WU Zhaohua, LONG S R,etal. On instantaneous frequency [J]. Advances in Adaptive Data Analysis, 2009, 1(2):177-229.

[6] PAI P F. Nonlinear vibration characterization by signal decomposition [J]. Journal of Sound and Vibration, 2007, 307(3/4/5):527-544.

[7] BOGOLIUBOV N N, MITROPOLSKI Y A. Asymptotic Methods in the Theory of Non-Linear Oscillations [M]. New York:Gordon and Breach, 1961.

[8] BEDROSIAN E, RICE S O. Output properties of Volterra systems (nonlinear systems with memory) driven by harmonic and Gaussian inputs [J]. Proceedings of the IEEE, 1971, 59(12):1688-1707.

[9] NUTTALL A H, BEDROSIAN E. On the quadrature approximation to the Hilbert transform of modulated signals [J]. Proceedings of the IEEE, 1966, 54(10):1458-1459.

[10] SCHMIDT G, TONDL A. Non-Linear Vibrations [M]. Cambridge:Cambridge University Press, 2009.

[11] PENG Z K, TSE P W, CHU F L. An improved Hilbert-Huang transform and its application in vibration signal analysis [J]. Journal of Sound and Vibration, 2005, 286(1/2):187-205.

[12] PENG Z K, TSE P W, CHU F L. A comparison study of improved Hilbert-Huang transform and wavelet transform:Application to fault diagnosis for rolling bearing [J]. Mechanical Systems and Signal Processing, 2005, 19(5):974-988.

[13] 纪跃波,秦树人,汤宝平. 零相位数字滤波器[J]. 重庆大学学报(自然科学版), 2000, 23(6):4-7.

JI Yuebo, QIN Shuren, TANG Baoping. Digital filtering with zero phase error [J]. Journal of Chongqing University (Natural Science Edition), 2000, 23(6):4-7. (in Chinese)

Nonlinear system identification based on instantaneous characteristics of dynamic response

QIN Anzhuang1, YANG Zhixun1, ZHANG Mingjie2, WU Wenhua1, ZHANG Wenshou*1

( 1.Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China；2.School of Civil Engineering, Dalian University of Technology, Dalian 116024, China )

In the light of the Krylov-Bogoliubov-Mitropolski (KBM) method, a nonlinear system identification method is developed based on the instantaneous characteristics of the dynamic response of the system. The method identifies all the system parameters through establishing function relationship connecting system transient response characteristics with system parameters. The normalized Hilbert transform (NHT) and the generalized zero-crossing(GZC) method are introduced to calculate the instantaneous amplitude and frequency of the dynamic response. An example is applied to verify the efficiencies of these two methods. The proposed system identification method is applied to the nonlinear vibration systems of the Duffing and Vanderpol equations. Experimental results show that the method has good identification accuracy even when the dynamic responses are largely polluted by noises.

instantaneous frequency; normalized Hilbert transform; generalized zero-crossing method; nonlinear system identification

2016-06-02；

2017-03-16．

国家自然科学基金资助项目(11572072).

秦安壮(1991-)，男，硕士生，E-mail:zuoyetingfeng@126.com；张文首*(1963-)，男，博士，教授，E-mail:wszhang@dlut.edu.cn.

1000-8608(2017)03-0221-06

TN911.6；O32

A

10.7511/dllgxb201703001