基于绿波带中心线交点的双向绿波控制图解法

陈 昕，张 驰



基于绿波带中心线交点的双向绿波控制图解法

陈 昕，张 驰

（辽宁工业大学 汽车与交通工程学院，辽宁 锦州 121001）

为解决传统图解法在双向绿波控制设计中绿波带带宽窄、反复调整以及求解相位差误差较大的问题，提出一种基于绿波带中心线交点的双向绿波控制图解法。首先，分析交叉口的不同放行方式对绿波带中心线交点位置的影响，而绿波带中心线交点位置又能够影响绿波带的带宽；然后，提出寻找合适的绿波带中心线交点来提高绿波带带宽的原则；最后，给出图解法具体的步骤。实例分析表明：该图解法能够提高双向绿波带带宽，对交叉口采用不同的放行方式均具有较好的适用性。

双向绿波；NEMA相位；图解法；绿波带带宽

绿波控制是指交叉口之间实行绿波运行的控制方式[1]，绿波控制能够减少车辆在各个交叉口上的停车时间以及停车次数。只考虑单个行进方向的交通控制方式叫单向绿波控制，同时考虑上、下行两个行进方向的交通控制方式叫双向绿波控制，双向绿波控制要比单向绿波控制实施起来困难。

双向绿波控制设计方法主要有图解法、数解法和模型法。图解法是在时间-距离图上协调线控系统的时差，同时调整并确定通过带速度和周期时长[2]；相对于数解法和模型法，图解法具有简单、直观、方便应用的优点。在绿波控制方面的研究，卢凯、林晓辉[3-4]等给出了各进口单独放行方式下绿波控制的算法及设计方法，卢凯、姬利娜[5-6]等给出了非对称方式下的绿波控制设计方法，朱和[7]给出了灵活相位设置下双向绿波控制设计方法，卢顺达[8]对非对称方式下图解法进行了改进设计。总结已有研究成果可以看出，对双向绿波控制研究大都只针对进口单独放行、非对称方式进行了研究，而对交叉口放行方式无约束的方法的研究较少；另外，对绿波控制设计方法的研究多停留在对绿波控制算法特别是对数解法的改进方面上，对图解法的研究较少。卢顺达、常玉林[8-9]等虽提到了可以运用图解法并采用灵活的相位设计来提高绿波带的带宽，但并没有给出相位相序设计的具体方法。鉴于此，笔者运用NENA TS2标准[10]中规定的双环相位结构来对交叉口的相位相序进行灵活的设计，提出一种适用于不同放行方式下的基于绿波带中心线交点的双向绿波控制图解法（以下简称交点式图解法）。

1 双环相位结构的相位相序设计

干线交叉口合理的相位相序设计以及交叉口采用何种放行方式对绿波控制设计有重要意义[11]。由于传统的相位相序设计方法不灵活，通过引入双环相位结构对交叉口相位相序进行设计，可以有效提高相位相序设计的灵活性。

在NEMA双环相位结构中，规定由1、2、5、6组成的相位组与3、4、7、8组成的相位组由一条“隔离线”分开，即2、6相位必须同时结束，3、7相位必须同时获得通行权。通常，相位组1分配给主干路，相位组2分配给次干路。环1由相位1—2—3—4组成，环2由相位5—6—7—8组成[12]。隔离线的存在，可以避免隔离线两侧不同控制环上的冲突相位在同一时刻启动。在隔离线两侧，两个控制环之间的相位选择应注意两点：（1）在同一个控制环上的相位是互相冲突的，不能同时运行；（2）隔离线一侧的不同控制环上的相位可以同时运行。采用NEMA双环相位结构，在保证以上两点的前提下，可对相位相序进行灵活的设计，为交叉口采用不同放行方式设计提供了便利。

图1 NEMA双环相位结构

2 交点式图解法

传统图解法的基本思路是通过几何作图的方法画出时间-距离图，首先建立交互式或者同步式协调，然后再对车速和公共周期时长进行反复调整，从而确定相位差，最终获得较为理想的绿波带宽。这种方法没有考虑交叉口宽度、相位相序设置对双向绿波设计中绿波带带宽的影响，需要对速度以及公共周期进行反复调整。对于一个需要进行绿波控制的干道，车速、公共周期时长一般会预先确定，传统图解法对速度、公共周期时长的反复调整与实际情况不符，采用传统图解法设计的双向绿波带带宽较窄，甚至无法实现双向绿波控制。

针对传统图解法的不足，笔者提出了交点式图解法，下面对交点式图解法的依据和步骤分别做出介绍。

2.1 交点式图解法的依据

交叉口相位相序的设计会影响交叉口绿波带中心线交点（绿波带中心线交点是指某一交叉口上、下行协调方向绿波带中心线相交的点）的位置，而交叉口采用不同的放行方式会有不同的相位相序，因此交叉口采用不同的放行方式会造成交叉口绿波带中心线交点的位置不同。常见的放行方式一般为对称放行、搭接放行以及各进口单独放行，采用对称放行方式，绿波带中心线交点与交叉口中心重合；采用搭接放行方式，绿波带中心线交点比较接近交叉口中心；采用各进口单独放行方式，绿波带中心线交点远离交叉口中心。三种典型的交叉口放行方式对应的相位相序设置方式一般较固定，图2给出了不同放行方式下相位相序的设置方法以及绿波带中心线交点与交叉口中心的位置关系。

在具体进行绿波控制方案的设计时，应根据道路实际交通情况进行灵活的相位相序设计，遵循的原则是：通过协调方向上平均车速确定交叉口理想间距，寻找合理的相位相序设计，使临近交叉口的各个绿波带中心线交点之间的水平间距尽量为零或者为交叉口理想间距整数倍（一般情况下绿波带中心线交点之间的水平间距与交叉口理想间距相等）。

（A）对称放行方式下绿波带中心线交点与交叉口中心重合

（B）搭接放行方式下绿波带中心线交点在交叉口中心附近

（C）各进口单独放行方式下绿波带中心线交点远离交叉口中心

2.2 交点式图解法的步骤

按照上文提出的原则，以下给出交点式图解法的具体步骤。

步骤一：画出时间-距离图。根据公共周期、协调方向的绿灯显示时间、交叉口间距、交叉口的宽度等数据画出时间-距离图。

步骤二：计算交叉口之间的理想距离。根据协调方向的平均车速以及公共周期时长按照公式（1）求出各个交叉口之间的理想间距。

其中：为绿波控制路段行驶车辆的平均车速；为公共周期时长；为理想交叉口间距。

步骤三：相序设计。通过合理的设计交叉口信号相序，使临近交叉口的各个绿波带中心线交点之间的水平间距尽量为零或者为交叉口理想间距的整数倍。通过反复调整相位的顺序，找到最合适的相序设置方式，从而最终确定各个交叉口信号配时方案。

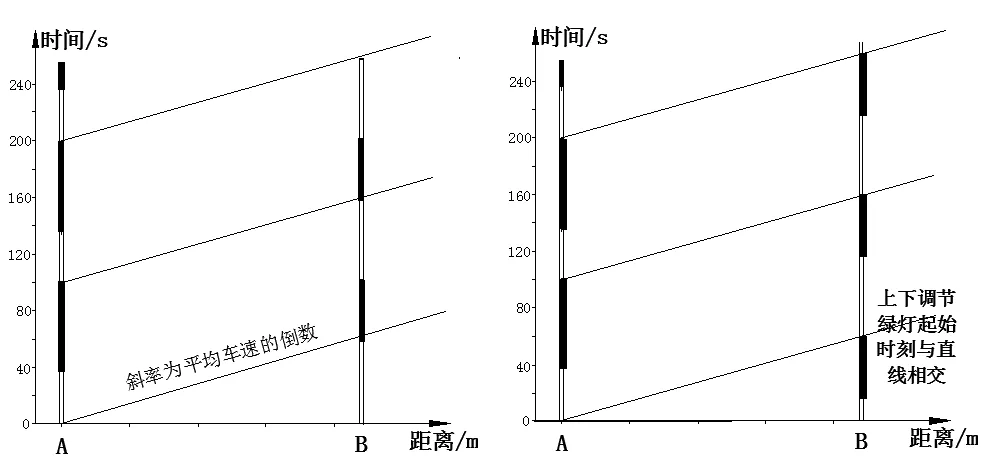
步骤四：改变各个交叉口的周期起始时刻，找到上、下行方向的最大绿波带带宽。具体做法是：在上行方向，画一条代表绿波带带速的直线，直线的斜率为平均车速的倒数，以该直线为参考，在时间-距离图上上下拖动改变各个交叉口的绿灯的起始时刻，使得直线与协调相位绿灯开启时刻相交；然后，在下行方向画代表带速的直线，以同样的方法进行调节，直到找到上、下行方向最大的绿波带为止。绿波带带宽的确定过程如图3所示。

步骤五：读取绿波带的带宽以及相位差。根据时间-距离图计算出绿波带带宽并确定各个交叉口的相位差（如图4所示），进而确定最终信号控制方案。

图4 上、下行方向绿波带带宽及相位差

3 实例分析

以青岛市金山路为例来说明交点式图解法在双向绿波设计中的有效性。金水路各个交叉口之间的距离较短，交通干扰较小，适合双向绿波控制。笔者选取金水路中的金水巨峰至金水合川路段作为双向绿波控制的对象，运用交点式图解法对金水路从西向东依次穿过巨峰路、奇峰路、宜川路、金川路、延川路、灵川路、铜川路、合川路形成的8个信号控制交叉口进行双向绿波设计。

根据交叉口的渠化状况和交通流量计算单点信号配时方案，把最大周期100 s作为公共周期，并把该交叉口作为关键交叉口，其他交叉口以该交叉口为参考对各个相位的显示时间进行调整。表1给出了交叉口间距、各交叉口宽度、平均车速、公共周期等数据，根据表1的数据画出时间-距离图。

按照本文介绍的原则调整信号控制方案的相位顺序，确定相序，依次改变与之相邻上、下游交叉口的周期起始时刻，通过时间-距离图最终确定信号控制方案以及交叉口的相位差。图5（A）给出不考虑交叉口距离以及相位相序的金水路双向绿波的传统图解法时间－距离图，图5（B）给出了金水路双向绿波改进的时间-距离图。

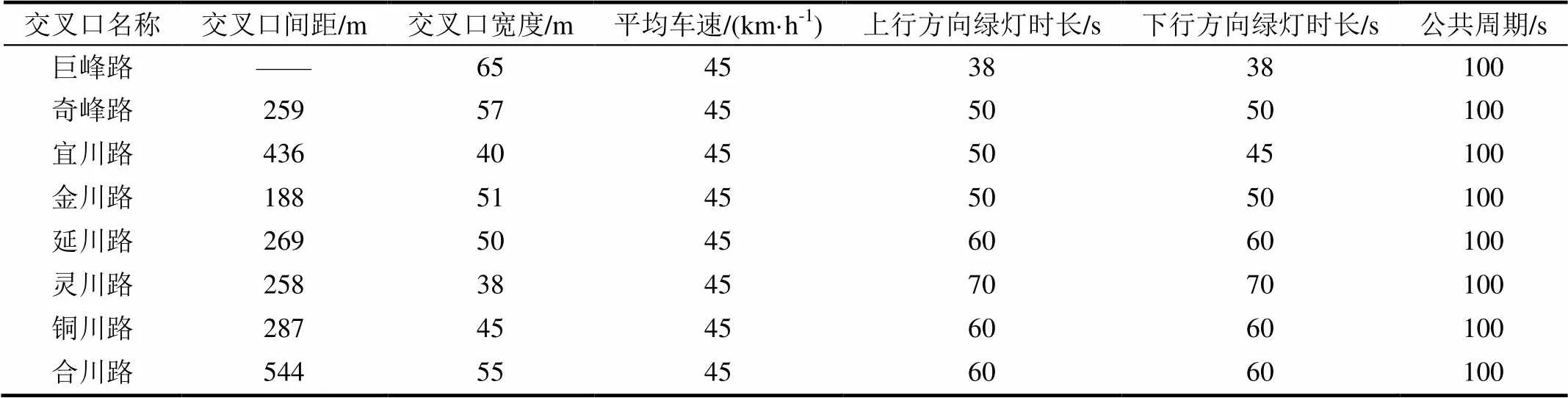
表1 绘制时间-距离图的基础数据

说明：交叉口间距指上行（西向东）方向相邻两交叉口停车线之间的距离；交叉口宽度指同一交叉口上、下行方向停车线之间的距离；宜川路交叉口上、下行方向绿灯时长不等。

（A）传统图解法的时间-距离图

（B）交点式图解法的时间-距离图

图5 图解法的对比效果

采用不考虑交叉口距离以及相序调整的传统的图解法得到的结果是：上行方向绿波带带宽为36%，绿波带带宽可达度为95%；下行方向绿波带带宽为21%、22%（绿波带在金川路交叉口断开），绿波带带宽可达度为55%、58%。采用交点式图解法得到的结果是：上行方向绿波带带宽为38%，绿波带带宽可达度为100%；下行方向绿波带带宽为30%，绿波带带宽可达度为79%。通过两结果对比可以看出，交点式图解法不仅提高了双向绿波带的带宽，也没有出现绿波带断开的情况，有利于双向绿波的设计。

4 结论

交点式图解法应用到金水路双向绿波的设计中，结果表明该图解法对交叉口不同放行方式下的双向绿波设计能够提高绿波带带宽，已在实际应用中得到了交警的认可。然而，交通流处在不断变化之中，随着交通流量的增加，需要对绿波控制进行不断地调整；同时，在现实情况下具体的相位相序设计会受到交通实际情况的限制。

[1] GB/T 31418—2015. 道路交通信号控制系统术语[S]. 2015.

[2] 吴兵, 李晔. 交通管理与控制[M]. 北京: 人民交通出版社, 2009.

[3] 卢凯, 徐建闽, 李轶舜. 进口单独放行方式下的干道双向绿波协调控制数解算法[J]. 中国公路学报, 2010, 23(3): 95-101.

[4] 林晓辉, 徐建闽, 卢凯, 等. 各进口单独放行条件下的双向绿波设计方法研究[J]. 交通与计算机, 2007, 25(5): 8-12.

[5] 卢凯, 刘永洋, 吴焕, 等. 非对称通行条件下的双向绿波协调控制数解算法[J]. 中国公路学报, 2015, 28(6): 95-103.

[6] 姬利娜, 宋清华. 非对称放行方式下的干道双向绿波协调控制[J]. 公路交通科技, 2011, 28(10): 96-101.

[7] 朱和, 常玉林. 基于灵活相位的双向绿波协调控制[J]. 公路交通科技, 2013, 30(7): 140-143, 158．

[8] 卢顺达, 程琳. 非对称相位相序方式下的双向绿波协调控制图解法的改进[J]. 公路交通科技, 2015, 32(1): 128-132．

[9] 常玉林, 张其强, 张鹏. 城市干线双向绿波控制改进设计[J]. 重庆理工大学学报, 2014, 28(12): 108-112.

[10] NEMA. NEMA standards publication TS-2 [S]. 2003.

[11] GA/T527.1—2015. 道路交通信号控制方式第1部分：通用技术条件[S]. 2015.

[12] 蔡云, 杨晓光, 王浩. 一种灵活的在线交通信号相位切换结构[J]. 城市交通, 2009, 7(3): 80-85.

责任编校：刘亚兵

Graphic Method of Bidirectional Green Wave Control Based on Centerline Intersection of Green Wave Band

CHEN Xin, ZHANG Chi

（Automobile & Transportation Engineering College, Liaoning University of Technology, Jinzhou 121001, China）

To solve these problems caused by traditional graphical method such as bandwidth of green wave, continuous adjustment and the greater error of phase in the design of bidirectional green wave control band, a kind of graphic method is proposed in the bidirectional green wave based on the intersection center line. First, the influence of different release modes on the intersection of centerlines in position of green wave band is analyzed while the centerline intersection in position of green wave band also has an effect on bandwidth green wave band; then, the principles of widening bandwidth of green wave band are presented through finding out the ideal position in centerline intersection of green wave band; finally, the concrete steps of graphic method are given. The analysis of calculation examples shows that the graphic method can widen bandwidth of bidirectional green wave band and has widely better applicability in different releasing methods at the intersection.

bidirectional green wave; NEMA phase; graphic method; green wave bandwidth

10.15916/j.issn1674-3261.2017.02.016

U491

A

1674-3261(2017)02-0137-04

2016-08-30

陈昕(1972-)，女，辽宁铁岭人，教授，博士。