准确理解教材意图，精心设计教学过程——以“利用圆设计美丽的图案”为例

人民教育出版社小学数学室 丁国忠

准确理解教材意图，精心设计教学过程
——以“利用圆设计美丽的图案”为例

人民教育出版社小学数学室 丁国忠

数学的基础知识、基本技能、基本思想、基本活动经验的培养，以及发现和提出问题、分析和解决问题能力的发展，需要在具体的教学过程中加以落实，前提是对教材编写意图的准确把握。“利用圆设计美丽的图案”是修订后的人教版小学数学教材中新增的内容，意在使学生通过深度参与数学探究活动，深入理解数学本质，提高数学学习兴趣。在教学这一内容时，要准确理解教材编写的这一意图，精心设计教学过程，创设有意义的真实情境，唤起学生的探究欲望，层层分析，剥茧抽丝，完整地经历问题解决的过程。在此过程中，使学生对“圆心决定圆的位置，半径决定圆的大小”有更深刻的理解，并产生进一步探索数学世界的愿望，实现数学核心素养的真正提升。

理解 意图 设计 过程 圆 图案

《义务教育数学课程标准（2011年版）》指出：“数学教学活动，特别是课堂教学应激发学生兴趣，调动学生的积极性，引发学生的数学思考，鼓励学生的创造性思维……”“学生学习应当是一个生动活泼的、主动的和富有个性的过程。认真听讲、积极思考、动手实践、自主探索、合作交流等，都是数学学习的重要方式。学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程。”数学的基础知识、基本技能、基本思想、基本活动经验的培养，以及发现和提出问题、分析和解决问题能力的发展，只有在具体的教学过程中才能得以落实。修订后的人教版小学数学教材非常重视通过相关的数学活动实现夯实“四基”、发展“四能”的教学目标。本文试以“利用圆设计美丽的图案”这一数学活动为例，谈一谈如何在准确理解教材编写意图的基础上，精心设计教学过程，使学生深度参与数学探究活动，深入理解数学本质，切实提高数学学习的兴趣。

一、准确理解教材意图

“利用圆设计美丽的图案”是在学生认识了圆、了解了圆的特征之后新增的一个数学活动。

关于“圆的认识”的编排，在本次教材修订时，我们进行了大胆的尝试。首先，呈现生活中各种圆的实例。接下来，与实验教材相似，修订后的教材依然安排了画圆的环节，所不同的是在这一环节中增加了用圆规画圆的内容（在过去，用圆规画圆一般是在认识圆的特征之后单独学习）。这样调整，一方面是由于大多数学生已经具备了用圆规画圆的生活经验，教材编排应充分考虑学生的认知起点；另一方面，通过用圆规画圆来引出圆心、半径、直径等概念，更能反映圆“一中同长”的本质特点。关于圆的特征的认识，由于在前面的“轴对称”单元中已经涉及圆的对称性，因此在本单元不再重复描述；同时，考虑到圆心与半径是体现圆的本质特征的两个要素，因此增加了“圆心决定圆的位置，半径决定圆的大小”这一特征，从圆的解析式（x-a）2+（y-b）2=r2可以看到，一旦一个圆的圆心和半径确定了，这个圆也就唯一地确定了。

用圆可以设计许多漂亮的图案，下面的图形就是用圆规和直尺一步一步画出来的。

请你试着用圆规和直尺画一画下面的图形。

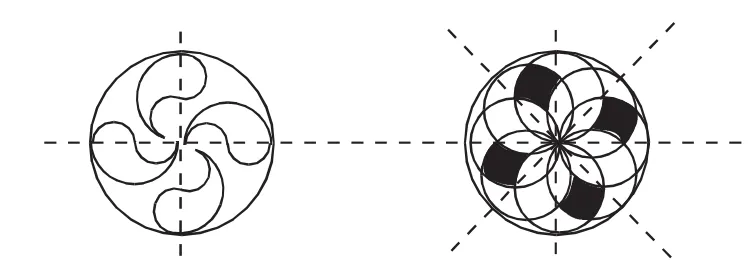
在此基础上，教材新编了“利用圆设计美丽的图案”的数学活动（如上图）。教材按两个层次进行编排：第一层次，方法示范。教材提供了一个相对简单的花瓣图案，并详细展示了如何利用圆规和直尺一步一步画出这个图案的过程，使学生掌握利用圆绘制给定图案的基本方法，并在此过程中深刻体会“圆心决定圆的位置，半径决定圆的大小”这一特征。第二层次，自主尝试。教材提供了两个稍复杂的图案，要求学生自己尝试画出来。为了降低学生的探索难度，教材特意给出了相关辅助线，给学生以简单的提示和引导。

对于圆这一大自然中最“和谐”的几何图形，圆本身以及利用圆设计出来的各种图案都能给人以很美的视觉感受，因此，利用圆设计图案有利于学生进一步欣赏数学之美。此外，以“设计图案”的真实需求代替生硬灌输，通过参与数学活动，使学生更深刻地体会到“圆心决定圆的位置，半径决定圆的大小”的特征，润物细无声。这样的活动，对于帮助学生学会透过现象看本质，提高发现和提出问题、分析和解决问题的能力，培养学生的探究意识和能力，更是大有裨益。

二、精心设计教学过程

在准确理解了教材的编写意图后，在进行教学设计时，可以紧扣以下目标：

第一，关注数学本质。使学生在利用圆规和直尺绘制给定图案的过程中，对“圆心决定圆的位置，半径决定圆的大小”有更深刻的理解。

第二，经历数学探究。在作图过程中，使学生提高观察、操作的能力，发展分析问题、解决问题的能力，丰富数学活动经验。

第三，感受数学之美。使学生学会欣赏数学的美，提高利用圆进行图案设计和创作的兴趣和能力，培养良好的数学学习情感。

在实施教学时，既可以遵照教材的编排顺序，第一课时教学“圆的认识”，第二课时教学“利用圆设计图案”，这样设计，只是将设计图案这一活动定位于第一课时知识的巩固与应用。也可以采用更大胆的设计方案：直接从研究“如何设计一个花瓣图案”这一大问题入手，对本小节内容进行整体性设计，第一课时解决“图案外部的大圆”的问题，第二课时解决“图案内部的四个半圆”的问题。在这样的设计思路下，所有知识的学习都是在特定的任务驱动下展开，而不是“为学而学”，更能体现“问题解决”的教学思想。两种设计方案各有特点，可视具体学情灵活采用，本文不重点展开讨论。

如果只聚焦于“利用圆设计美丽的图案”本身，在进行教学设计时可遵循由简单到复杂层层推进、详略有别、收放有度的原则。

1.简单图案的绘制

这一环节，以绘制比较简单的花瓣图案为载体，使学生大致掌握绘制给定图案的基本方法。

教学时，可从教材上呈现的花瓣图案直接导入。笔者也一直苦于没有找到这一图案的生活原型，直到某次出差，很偶然地在南宁滨湖路小学的校园里见到了与教材上一模一样的图案（如下图）。若能以这样一个自然、真实的情境导入，一定更能激发学生的探究兴趣。

在呈现这样的实际情境以后，可让学生思考：这个图案是怎样画出来的？先让学生尝试自行解决。也许，大部分学生在探究过程中会遇到困难，但真正的探究应该让学生有机会遭遇这样的障碍。有了障碍，才能产生问题，有了问题，才能产生思考，接下来的探究过程才会真正有效。

在学生遇到困难、产生探究欲望后，师生再以“问题串”的形式，共同探索解决这个问题的基本思路：在这个漂亮的花瓣图案中，你看到了哪些几何图形？遇到的主要困难是什么？如果看不太清楚的话，把颜色去掉是不是更明显一些？（根据学生回答，课件演示去掉颜色的过程，使学生发现图案外面是一个大圆，里面的四个“花瓣”是由四个小的半圆组成的）大圆好画吗？（在纸上确定了圆心和半径就可以画出来）这四个半圆能任意画吗？要画出它们，需要知道什么？它们的圆心和半径该怎样确定？（引导学生添加辅助线，依次连接四个半圆与大圆的四个交点，找到四个半圆的直径；通过测量相关线段的长度，就可以找到圆心和半径）假设已经画出了大圆，在大圆上怎样找到这四个点呢？（引导学生通过观察、思考，发现这四个点形成的图形是一个正方形，把这个正方形的对角线连起来，正好是大圆的一对互相垂直的直径）

以上的分析过程可用下图表示：

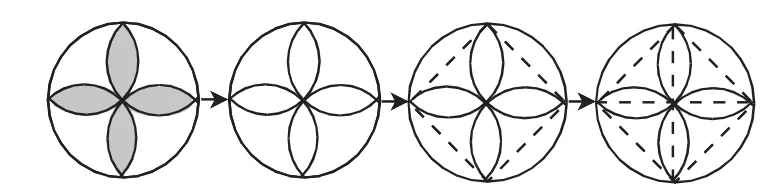
把图案分解、还原的思路分析清楚后，再来思考如何绘制出这个图案。绘制的过程恰好就是以上分析过程的逆向操作：先确定好圆心、半径，画出一个大圆。再画出大圆的一组互相垂直的直径，这两条直径和大圆有四个交点，把这四个交点依次连接起来，再以这四条线段分别为直径画出四个半圆。最后，把这些辅助的线段擦去，并涂上自己喜欢的颜色，就形成了一个漂亮的花瓣图案。这一环节可以让学生自主完成。

接下来，通过交流反馈，引导学生回顾整个探究过程，整理思路。（1）分析：先去掉颜色的干扰，找出组成图案的基本图形，并发现这些基本图形之间的关系（圆心的位置、半径的大小）；再通过添加辅助线等手段找到画出基本图形的方法。（2）绘制：对分析的过程进行倒推，先一步一步画出基本图形，形成图案的轮廓，再在相应部分涂上自己喜欢的颜色。

最后，可以引导学生把涂好颜色的作品进行交流、展示，让学生看到，尽管大家绘制的图案大小、颜色不同，但分析与绘制的方法是一致的，图案中大、小圆之间的关系也是一致的。

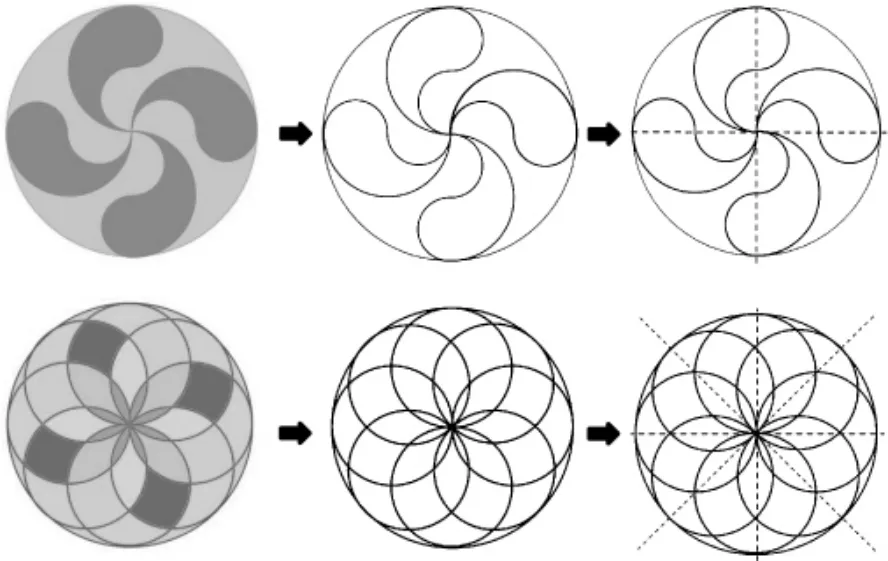
2.稍复杂的图案的绘制

与第一环节相比，这一环节可体现更大的开放性，放手让学生自主探索。基本的分析过程如下图：

3.欣赏与拓展

一堂好的数学课，下课铃响不应是学习活动的结束，而应该是新的学习活动的开始。本活动中，只是绘制了相对简单的图案，而且是绘制给定的图案。在学生掌握了基本的分析方法后，可引导学生将课内所学进行更多的拓展性应用。例如，课后可由教师提供，也可由学生自行上网找到更多与圆相关的美丽图案（如下图）进行欣赏，并尝试着绘制一下。

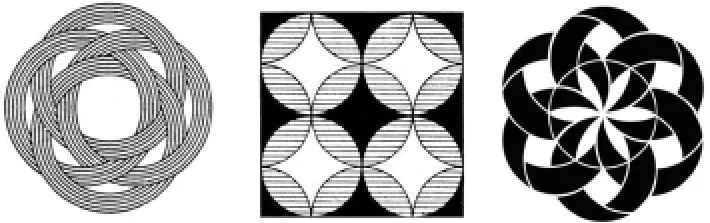
除此之外，还可进一步发挥学生的创造性，激发学生自由创作的愿望，在创作中领略数学之美。即使是已经画过的图案，也可体现更大的开放性：涂色方法不同，效果也迥异。例如，教材上最后一个图案，还可涂画出更多类似于下图的作品。

以下是一些学生自由创作的作品：

由此可见，只要给学生充分的自由探究的时间和空间，他们会还以更大的惊喜。或许，某些学生会因为这一数学活动而爱上数学、爱上设计，而在数学和艺术的道路上走得很远，这也是我们在修订教材时新编这一活动的一个更高、更远的期望。从这个意义上讲，把这一数学活动做成一个“综合与实践”的生动案例，是完全有可能的。甚至，还可将本活动的实施作为一个契机，在班内、年级内开展一次图案设计大赛，真正实现课程的融合。

在以上教学活动中，学生通过动脑、动口、动手，完成了一次将数学应用于艺术设计的探究之旅。在这一过程中，“四基”“四能”得以真正落地生根、发芽：学生不仅巩固了“圆心决定圆的位置，半径决定圆的大小”这一基础知识，提高了测量、画圆等基本技能，更为重要的是，进一步理解和掌握了抽象、推理、审美等数学思想，积累了更加丰富的数学活动经验。

眼下，培养学生的数学核心素养成为数学教育和教学的重要任务，相关的理论研究与讨论非常热烈。笔者认为，学生数学核心素养的培养，不是一句空泛的口号，需要在每一个实实在在的教学活动中加以落实。正如马云鹏老师所指出的：“数学核心内容是培养数学核心素养的载体。”“学生的有效参与是培养核心素养的重要途径。”“深度探究是发展核心素养的关键。”在数学教学中，只有创设真实而有意义的情境，才能使学生真正学会“用数学的眼光观察世界”；只有让学生深度参与数学探究的全过程，才能使学生真正学会“用数学的思维分析世界”；只有引领学生将数学应用于现实世界，才能使学生真正学会“用数学的语言表达世界”。

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]人民教育出版社课程教材研究所小学数学课程教材研究开发中心.义务教育教科书数学六年级上册[M].北京：人民教育出版社，2014.

[3]史宁中.数学的基本思想[J].数学通报，2011（1）.

[4]马云鹏.小学数学教学中核心素养的培养——以吴正宪老师“小学除法”教学为例[J].小学数学教育，2016（11）.