构建“培养几何直观能力”的练习课
——“图形与几何”练习课教学改进与创新有感
浙江省余姚市实验学校 孙 洁
构建“培养几何直观能力”的练习课
——“图形与几何”练习课教学改进与创新有感
浙江省余姚市实验学校 孙 洁
“图形与几何”(测量)领域的练习课设计,除了让学生掌握“四基”外,更为重要的是通过练习培养学生的几何直观能力,发展学生的空间观念。学会用图形思考、想象问题是研究数学,也是学习数学的基本能力,这种能力的培养要贯穿于数学教学的全过程,而练习课则是一个重要的战场。
练习课;几何直观
在2011版课程标准颁布后,又开展了一轮“以学为中心”的课改攻坚战,在这样的背景下,小学教学课程及教学的研究将逐步深入并细微化,小学教学课堂中教学的方式方法发生了巨大的变化,从教师主宰课堂到教师的教与学生的学的统一;从教师讲学生听到丰富而有效的数学教学活动;从重视知道结论到重视为学生提供充足的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程;课堂教学目标从落实“双基”到落实基本知识、基本技能、基本思想和基本活动经验的“四基”等等。但当我们仔细品味其中时却不难发现,这一系列的改变更多指向的是数学教学中的新授课,而对于作为新授课补充与延续的练习课相比之下却少有人问津。
这些年,笔者进行了“图形与几何”(测量)领域练习课教学改进与创新的实践,下面谈谈粗浅的经验。
一、练习课改进与创新的实践目标
构建“基于培养几何直观能力的练习课”是本次课堂研究的实践目标。几何直观主要是指利用图形描述和分析数学问题。借助几何直观可以把复杂的数学问题变得简明、形象,有助于探索解决问题的思路,预测结果。“图形与几何”(测量)领域的练习课设计,除了让学生掌握“四基”外,更为重要的是通过练习培养学生的几何直观能力,发展学生的空间观念。学会用图形思考、想象问题是研究数学,也是学习数学的基本能力,这种能力的培养要贯穿于数学教学的全过程,而练习课则是一个重要的战场。要摒弃以训练解题能力、获取解题技巧为目的的设计理念,而应结合学生的实际,设计针对的题型,有利于学生的想象和操作,进而培养学生的几何直观。
二、练习课改进与创新的理论基础
基于“培养几何直观能力”的练习课的改进与创新需要实践研究的理论基础。建构主义理论和“做中学”理论能有效地指导练习课的改进与创新。
建构主义理论是学习理论认识心理学派的一个分支,它是行为主义发展到认知阶段后的进一步发展。建构主义认为人们通过个人的经历和图式来不断地建构个体对世界的认识,因此强调培养学习者在真实的情境中进行问题解决。建构主义理论强调:①学习是学习者主动建构内部心理表征的过程。②学习的建构过程包含两方面的建构,即对新信息意义的建构和原有经验的改造和重组,使学习者为自己的“经验流”建立一种秩序。③学习者以自己的方式建构对事物的理解,从而不同的人看到的是事物的不同方面,因此要增进学生之间的交流与合作,提倡合作学习。
“做中学”最早由美国著名教育家杜威提出,在历史发展过程中,研究者赋予了“做中学”更多的价值与内涵。美国著名教育家杜威提出了经验主义教育思想,为操作学习提供了理论基础和实践雏形。“做中学”的理念就在于“我听了,我忘了;我看了,我记住了,我做了,我明白了”,这种理念强调学生亲身经历的探索过程,通过自己观察、提问、假设、验证等活动,体验探索知识的过程,建构知识体系、形成一定的探究能力,积累活动经验和探究经验。
三、练习课改进与创新的基本模式
结合研究目标,本次实践重点研究了基于“培养学生几何直观能力”的练习课教学的基本流程与操作范式,初步建立练习课的课堂教学的基本模式,如下图:

以六年级下册《圆锥的体积》练习课为例,具体如下:
①收集错例——这是课堂教学前的环节。教师依据新授课的教学内容,组织进行前测或审阅学生的作业本,收集相关典型的错题。
②展示讲评——结合学生的错题汇总,引导学生先进行自我解剖:这些题目错在哪里?为什么会产生这样的错误?应该怎样改正?这个环节为下一步的练习进行知识上的自我回顾和纠正。

通过学生错例的展示,让学生思考错误的原因,由于错误资源来源于学生,因此可以激发学生学习的主动性。通过错例原因的反思,不但给了错误学生再次回顾圆锥体积计算方法的机会,而且让全体学生进一步体验到良好的学习习惯的重要性。
③基础巩固——以全班学生为目标,设计基础性的习题,巩固学生的基础知识,培养基本技能,以达到保底的目标。



④典型练习——这是课堂教学中的主要环节,结合数学知识点,以培养学生的几何直观能力为核心目标,设计出相关的习题,便于学生进行空间想象和动手操作,以此达到课堂的教学目标。

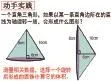

培养学生的“几何直观”是图形与几何教学的核心理念,而想象和画图是培养学生几何直观能力有效的途径之一。从一个平面的直角三角形入手,让学生先想象旋转后的图形的形状,再画出这样的立体图形,进而选择一个圆锥进行体积的计算,这样的设计不但进一步巩固了圆锥体积的计算方法,而且有效地培养了学生的空间观念,学生的思维从一维空间发展到二维空间。同时,沿斜边旋转和钝角三角形的旋转提升了思维的含量,激发了学生的探索欲望。
⑤应用拓展——这不是数学知识点的简单重复练习,而是对原先学习过的内容进行综合提升后的练习,是一个使学生对所学知识达到深入理解、融会贯通、牢固掌握,提高数学知识应用能力和技能的过程,更是学生获取解题的不同策略,感悟数学思想方法,提高解决实际问题能力的重要环节。

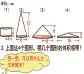
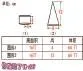

新课标指出“学会用图形思考、想象问题是研究数学,也是学习数学的基本能力,这种能力的培养要贯穿于数学教学的全过程。”因此,设计练习题时让学生根据提供的信息先想象出这个立体图形,再画出这个立体图形,就是把头脑中的几何形象进行物化,这是一种培养学生几何直观的有效方法。而在比较图形体积的过程中,允许不同的学生运用不同的方法进行解答,不但尊重了学生作为学习主体的地位,更让学生积累了解决问题不同策略的数学活动经验。把学生课堂生成的信息汇总成表,让学生进行观察探索,培养了学生的分析、推理和综合的能力,沟通了圆柱和圆锥体积计算之间的内在联系,更突出了体积与底面积和高之间的关系。及时的应用提升既巩固了学生发现的数学规律,又激发了学生探索数学的欲望。
⑥效果评价——这是一个完整教学的阶段性总结环节,主要由教师对个人自身的教学活动进行客观的自我评价,另外也要完成对学习者个人的学习评价。
综上所述,图形与几何的练习课的改进和创新,需要建立新的课堂教学模式,关注学生的数学核心素养,设计针对性的有利于学生想象和操作的练习题,在学生动手、动脑、动口的过程中培养学生的几何直观能力,发展学生的空间观念,做到“下要保底,上不封顶”,最终达到改变学习方式、提升学生的数学综合素养的目的。
[1]义务教育数学课程标准:2011年版[S].北京:北京师范大学出版社,2012(1).
[2]朱荣武.小习题 大习题[J].小学数学教师,2015(6):67.
[3]张佩玲,吕传汉.小学数学核心概念教学研究[M].贵阳:贵州人民出版社,2008(12):36-54.

