基于Anylogic的三级线性服装供应链存贮策略选择研究

摘 要：近些年来，随着全球制造和经济一体化的深入发展，服装企业间的竞争已逐步演变为服装供应链间的竞争。然而，供应链中的不确定性因素以及牛鞭效应，增加了服装供应链的整体库存水平。因此，如何降低服装供应链的库存水平对供应链的稳定高效地运行具有重要的影响。基于此，本文将运用仿真优化的方法来研究由1个制造商、1个分销商和1个零售商所组成的三级线性服装供应链存贮策略选择的问题，并通过实例验证其可行性。

关键词：Anylogic；服装供应链；存贮策略

中图分类号：F274 文献标识码：B 文章编号： 1674-2346（2017）01-0066-05

在全球制造和经济一体化推动下，服装企业间有关产品质量、价格、促销以及公关等方面的竞争已逐渐演变为由供产销各节点企业所构成的服装供应链之间的竞争。然后，服装供应链中存在的多重不确定性和由此产生的“牛鞭效应”（需求变异现象），增加了服装供应链的整体库存水平，这给链上各节点企业带来不必要的成本负担。因此，在终端服务水平不降的前提下如何降低服装供应链的库存成本就成为研究的热点。即科学、合理地设置各节点企业的存贮策略，不仅能降低服装供应链的库存成本，而且也能增强服装供应链的响应能力，最终实现链上的整体收益大于各节点企业独自运行时所获收益的总和。

1 问题描述

1.1 研究对象

为了满足消费者高品质、多样化、及时性的需求，供产销各节点企业通常以合作共赢、弱化分歧的思想加强彼此之间的合作紧密程度。在消费者的需求驱动下，负责服装产品销售的零售商会根据店面销售情况以及可用库存量向分销商订货；而负责服装产品推广的分销商会根据零售商的订货批量以及可用库存量向零售商发货或向制造商订货；负责服装产品生产的制造商则根据分销商的订货批量以及可用库存量向分销商发货或组织生产。其中，各节点企业以何种存贮策略将决定企业的库存水平，进而影响整条供应链的库存成本。基于此，本文将运用仿真优化的方法来研究由1个制造商、1个分销商和1个零售商所组成的三级线性服装供应链存贮策略选择的问题。

1.2 假设前提

假设1：各节点企业均采用（t，s，S）存贮策略，即：各节点企业每隔t时间检查其库存量I，当库存量I低于安全库存s时，分销商、零售商将向上游节点企业订货，且订货批量为S-I，而制造商则进行S-I批量的生产。

假设2：服装供应链所面临的外部需求具有不确定性，并假设在t时间段内，消费者的需求强度X是一个离散型随机变量，其分布律可通过历史数据分析知，而消费者购买产品次数服从均值为的泊松分布。

假设3：服装产品从制造商到分销商处的运输时间服从均匀分布，而服装产品从分销商到零售商处的运输时间也服从均匀分布。

假设4：消费者服务等待时间CSWT是指消费者付款后至拿到全部数量产品这段时间，且当产品缺货时，允许商家缺货回补。

假设5：服装供应链各节点企业间是合作伙伴关系，可忽略其竞争关系，即零售商只向分销商订货，以获取分销商所提供的多方优惠支持。

2 成本模型构建

2.1 服装供应链库存总费用

在每隔t时间内，服装供应链库存总费用TC由零售商库存总费用TR、分销商库存总费用TD以及制造商库存总费用TM 3部分组成，即TC=TR+TD+TM。

1）零售商（分銷商）库存总费用

零售商库存总费用、分销商库存总费用均由订货费、存贮费和缺货损失费3部分组成。其中，订货费=订购费+本期产品进货成本；存贮费=本期存贮量*单位存贮费；缺货损失费=本期缺货量*单位缺货损失费。

2）制造商库存总费用

制造商库存总费用包括生产费、存贮费和缺货损失费3部分。其中，生产费=装配费+本期产品生产成本；存贮费=本期存贮量*单位存贮费；缺货损失费=本期缺货量*单位缺货损失费。

2.2 服装供应链平均库存总费用模型

目标函数：minZ=（TR+TD+TM）/t

决策变量：各节点企业的安全库存和最高库存

约束条件：CSWT≤ （ 为常数）

各节点企业的安全库存其最高库存

3 系统仿真

3.1 系统各模块功能简介

为了确定各节点企业的安全库存和最高库存，本文将基于Multi-Agent的仿真建模技术，在Anylogic7.0仿真平台上再现各节点企业的业务流程。该仿真模型将设置4个Agent（MainAgent、零售商Agent、分销商Agent以及制造商Agent）和3个Java类（需求Java类、订单Java类以及装运Java类）。下面将分别说明各模块的主要功能。

3.1.1 Main Agent

Main Agent是模型的控制中心，通过对表函数（Table Function）、变量（Variable）以及事件（Event）的设置，将消费者的需求信息引入到仿真系统中，并通过连接器（Connector）实现零售商Agent、分销商Agent以及制造商Agent间的信息通信，同时通过分析库（Analysis库）的功能，实现对仿真运行时数据的实时性统计与分析。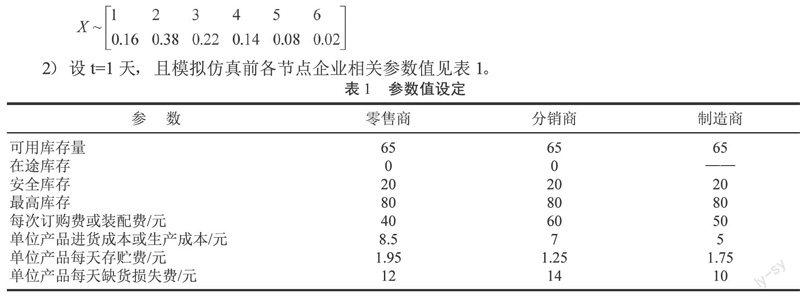

3.1.2 零售商Agent

零售商Agent主要实现满足消费者需求、向分销商订货、库存管理以及成本统计等功能。主要通过消费者需求处理、订货处理两个行动图（Action Chart）来实现。其中，零售商对消费者需求处理的业务流程如下：

（1）判断demands队列（消费者订单队列）是否不为空。若是，则定义demand局部变量，并令其初始值为demands队列中最早排队的订单二维信息值，然后转到（2）；若为空，则转到（4）。

（2）判断可用库存量是否大于零。若是，则转到（3）；若为零，则说明零售商无法供货给消费者，并转到（4）。

（3）判断可用库存量是否能够全部满足此单需求量。若能全部满足，则增加main中消费者服务等待时间集的值，并将demands队列中最早排队的订单出列，以及更新可用库存量，然后循环到（1）；如部分满足，则更新可用库存量，并转到（4）。

（4）更新零售商的存贮费和缺货损失费。

而零售商对订货处理的业务流程如下：

（1）定义IEB（库存量）局部变量，并令其初始值为可用库存量+在途库存-目前未能满足消费者需求的订单总量。

（2）定义O（订货批量）局部变量，当IEB<安全库存时，令O=最大库存-IEB；当IEB≥安全库存时，令O=0。

（3）判断O是否大于零，若是，则向分销商订货，并增加在途库存，以及增加订货费；若否，则结束订货。

3.1.3 分销商Agent

分销商Agent主要实现处理零售商订单、向制造商订货、库存管理以及成本统计等功能。主要通过业务处理行动图（Action Chart）来实现。其中，分销商业务处理流程如下：

（1）判断orders队列（零售商订单队列）是否不为空。若不为空，则定义order局部变量（临时变量），并令其初始值为orders队列中最早排队的订单二维信息值，然后转到（2）；若为空，则转到（3）。

（2）判断此单需求量是否小于等于当前可用库存量。若是，则向零售商发货，并将此单从orders队列中删除，以及更新可用库存量 ，然后循环到（1）；若为不是，则说明分销商无法供货给零售商，并转到（3）。

（3）定义IEB（库存量）局部变量，并令其初始值为可用库存量+在途库存-目前未能满足零售商需求的订单总量。

（4）定义O（订货批量）局部变量，当IEB<安全库存时，令O=最大库存-IEB；当IEB≥安全库存时，令O=0。

（5）判断O是否大于零，若是，则向制造商订货，并增加在途库存，以及增加订货费，然后转到（6）；若不是，则直接转到（6）。

（6）更新分销商的存贮费和缺货损失费。

3.1.4 制造商Agent

制造商Agent主要实现处理分销商订单、产品生产、库存管理以及成本统计等功能。主要通过业务处理行动图（Action Chart）来实现。其中，制造商业务处理流程如下：

（1）判断orders队列（分销商订单队列）是否不为空。若不为空，则定义order局部变量，并令其初始值为orders队列中最早排队的订单二维信息值，然后转到（2）；若为空，则转到（3）。

（2）判断此单需求量是否小于等于当前可用库存量。若是，则向分销商发货，并将此单从orders队列中删除，以及更新可用库存量，然后循环到（1）；若为不是，则说明制造商无法供货给分销商，并转到（3）。

（3）定义IB（库存量）局部变量，并令其初始值为可用库存量-目前未能满足分销商需求的订单总量。

（4）定义M（生产批量）局部变量，当IB<安全库存时，令M=最高库存-IB；当IB≥安全库存时，令M=0。

（5）判断M是否大于零，若是，则将触发Manufacturing动态事件以进行产品生产，并增加生产费，然后转到（6）；若不是，则直接转到（6）。

（6）更新制造商的存贮费和缺货损失费。

3.1.5 Java类

需求Java类：定义一个包含消费者需求量（amount）和需求发生时刻（timestamp）二维需求信息的Demand类。

订单Java类：定义一个包含订货商和订货量二维订货信息的Order类。

装运Java类：定义一个包含发货量信息的Shipment类。

3.2 仿真模型实现

借助Anylogic仿真软件所提供的优化实验（Optimization Experiment）功能，通过对参数（Parameters）、模型运行时间（Model time）、约束条件（Constraints）以及附加筛选条件（Requirements）的设置，每经过500次迭代后，可得一个关于存贮策略的备选方案组。然后根据各节点企业的实际情况，经过协商后可得供应链最优存贮策略。

4 案例分析

4.1 背景材料

為了适应现代化管理、提高企业竞争力，拟建关于服装制造商M、服装分销商D以及服装零售商R的三级线性供应链系统，实现产销一体化。通过各节点企业所提供的数据，可得下面相关信息：

1）根据消费者以往购买秋季男士休闲风衣的行为分析知，每天购买该产品的次数服从均值为10的泊松分布，而需求强度X的分布律为：

2）设t=1天，且模拟仿真前各节点企业相关参数值见表1。

3）服装制造商的生产能力远大于终端市场需求，且机器装配时间为0.8小时，每个产品的生产时间为0.03小时。

4）消费者服务等待时间CSWT不超过2.4小时（0.1天）。

5）该产品从服装制造商到服装分销商处的运输时间服从均匀分布，而该产品从服装分销商到服装零售商处的运输时间服从均匀分布。

4.2 仿真结果分析

设模型运行时间为365天，仿真10次，分别记录服装零售商R、服装分销商D以及服装制造商M的安全库存（s）、最高库存（S）、最优迭代次数以及服装供应链平均库存总费用的结果，具体见表2。

从表2中数据分析知，在供应链平均库存总费用在1575元左右波动时，服装零售商的安全库存均高于服装制造商的安全库存，同时服装分销商的安全库存也基本高于服装制造商的安全库存；服装零售商的最高库存均高于服装制造商的最高库存，同时服装分销商的最高库存也基本高于服装制造商的最高库存。

因而，可以认为：在市场需求不确定性因素的推动下，为了满足消费者高品质、多样化、及时性的需求，服装供应链中分销节点企业（分销商和零售商）通常将安全库存、最高库存设置较高，而服装供应链中制造节点企业（制造商）则为了及时地响应市场需求的变化会保有较高的原材料、半成品，进而达到各节点企业共赢的局面。即各节点企业可根据自身实际情况（比如仓库的最大容量、产品以往销售情况等），经协商后可得供应链最优存贮策略。

比如，服装零售商提出自身仓库的最大容量为68单位，服装分销商提出自身仓库的最大容量为70单位，服装制造商提出自身仓库的最大容量为60单位，则通过对表2中每组存贮策略进行筛选，可得该条线性供应链的最优存贮策略。即服装零售商的存贮策略为（64，68），服装分销商的存贮策略为（63，63），服装制造商的存贮策略为（55，58），且供应链的平均库存总费用为1577.032元。

参考文献

[1] LIU Z.H， WU L.R.Study on Countermeasures that Reduce Reverse Bullwhip Effect in County Retail Supply Chain[G]//2013 年教育技术与管理科学国际会议论文集，2013：1216-1219.

[2]马士华，林勇.供应链管理[M].北京：机械工程出版社，2015.

[3]林勇.供应链库存管理[M].北京：人民交通出版社，2008.

[4]江玉杰.基于改进Shapley 值法的装配供应链收益分配研究[J].山东交通学院学报，2015（01）：36-40.

[5]江玉杰，两级服装供应链库存模型研究[J].浙江纺织服装职业技术学院学报，2016（04）.

[6]蒋长兵，代应.库存控制：模型、技术与仿真[M].北京：中国物资出版社，2010.