变压器轴向固有频率分析计算
李阳阳
摘 要:本文采用“质量-弹簧-阻尼”模型等效绕组在短路过程中的轴向振动过程,研究了轴向预应力与绕组轴向固有振动频率的关系。
关键词:轴向固有振动频率;轴向预应力
0 引言
本文将对短路过程中绕组的轴向振动特性进行研究,振型和振动的固有频率是绕组振动的两大组成部分,而固有频率是研究的重点,其很大程度决定于绕组在振动中动态力的变化特性及幅值的大小,同时固有频率也决定了绕组是否会发生谐振。
1 绕组轴向振动固有频率的计算
绕组在短路电动力的作用下会引起辐向振动和轴向振动两种,两者都具有各自的固有振动频率。研究表明变压器绕组的辐向固有振动频率远远大于100Hz[1],因此目前对绕组辐向短路力均采用静态法对其进行分析计算。而电力变压器绕组的轴向尺寸远大于辐向尺寸,且绕组轴向振动固有频率通常小于100Hz,因此为保证计算的准确性,在计算绕组轴向短路电动力时需采用动态力方法求解。
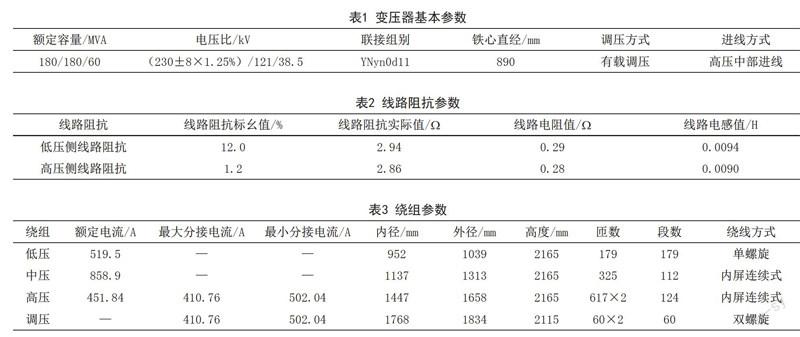
本文利用ANSYS有限元分析软件自编程序对一台220kV/180MVA三绕组有载调压电力变压器进行了分析计算。变压器的主要参数如表1、表2、表3所示。
上述变压器高压绕组进线方式为中部进线,上半部分绕组及下半部分绕组的额定电流为高压绕组额定电流的一半,所受短路电动力较小,故本文仅对该变压器中、低压绕组的轴向特性进行分析。
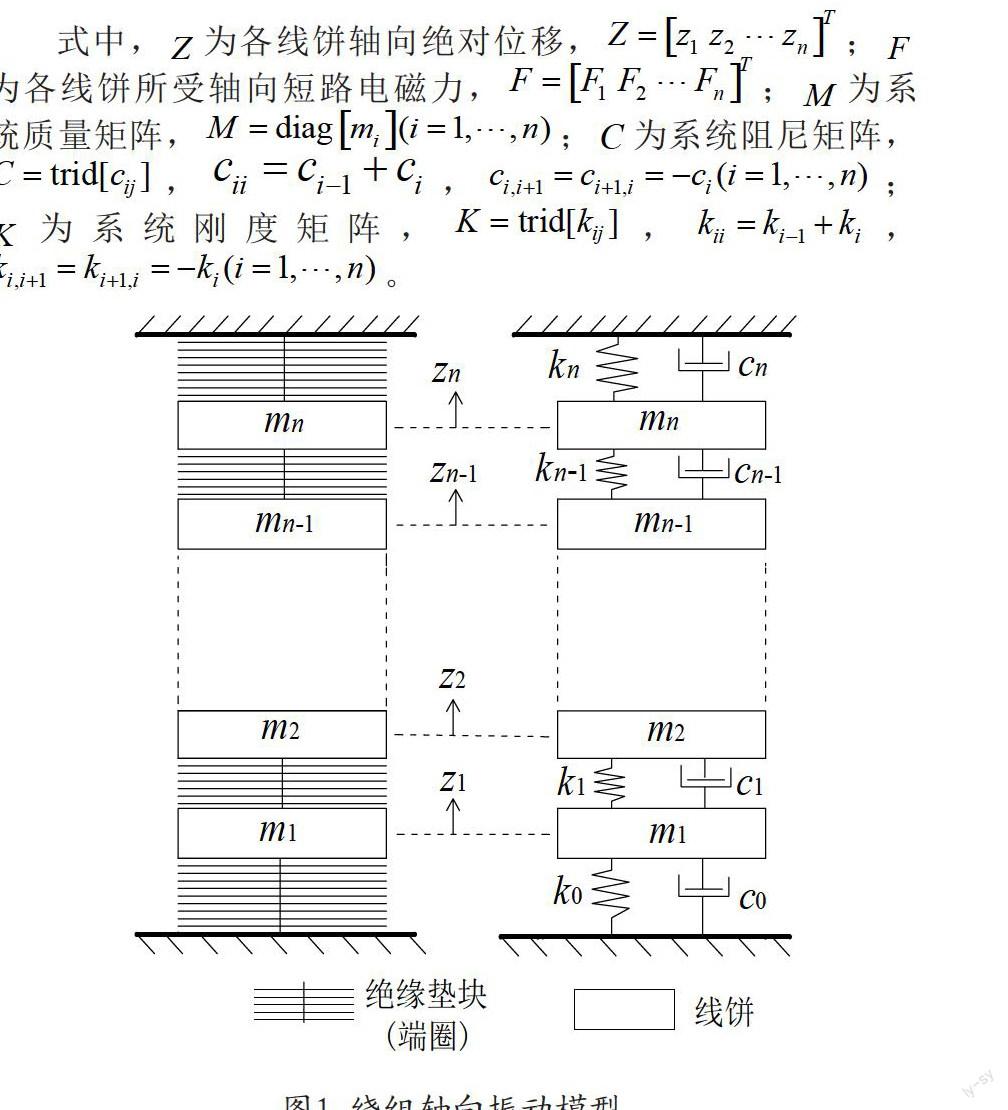
目前通常用集中质量-阻尼模型对变压器绕组进行等效,本文亦采用该模型对变压器绕组轴向振动特性进行研究,本文在建立“质量-弹簧-阻尼”模型时假设:(1)铁轭不随绕组振动而振动,且为绝对刚体;(2)绕组间的绝缘垫块不承受拉力、只承受压力;(3)绕组等效为集中质量的质点,垫块等效为不计及质量的弹簧。图1为用“质量-弹簧-阻尼”系统等效的绕组模型。
根据力学理论知识,绕组线饼满足下列方程[2]:
(1-1)
式中,为各线饼轴向绝对位移,;为各线饼所受轴向短路电磁力,;为系统质量矩阵,;为系统阻尼矩阵,,,;
为系统刚度矩阵,,,。
1.1 绕组轴向振动固有频率计算原理
绕组的轴向固有振动特性是由自身结构引起的,在式(1-1)中,不计及阻尼及外力下,绕组固有振动方程为:
(1-2)
上述方程的解可以表示为
(1-3)
式中,为绕组振动的主振型。
将式(1-3)代入式(1-2)可得
(1-4)
上述方程有非零解的条件是系数行列式等于零,即
(1-5)
由式(1-5)可得固有角频率
(1-6)
通过有限元方法求解“质量-弹簧”振动模型可求得n阶振动系统的n阶固有频率
(1-7)
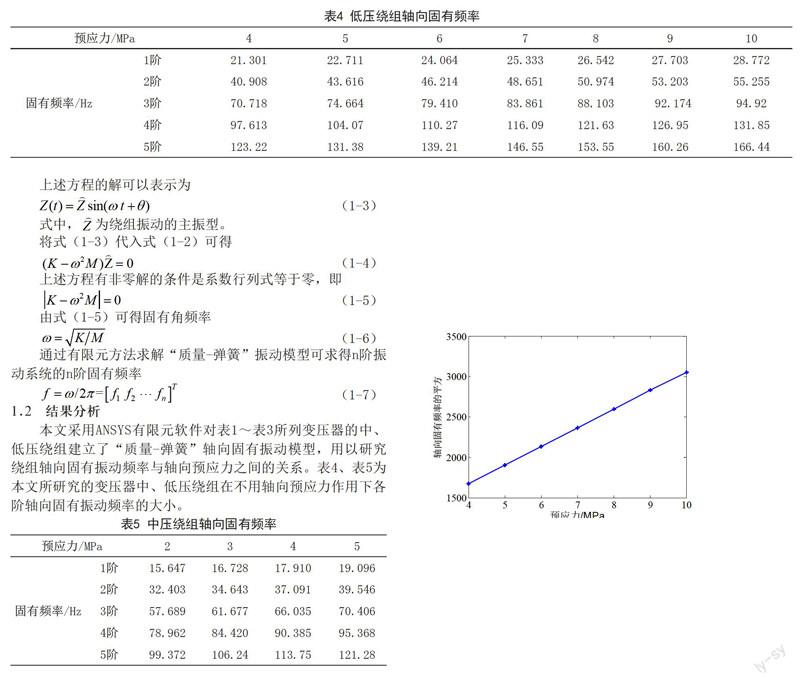
1.2 结果分析
文所研究的变压器中、低压绕组在不用轴向预应力作用下各阶轴向固有振动频率的大小。
2 结语
本文针对一台实际运行的电力变压器,采用ANSYS有限元软件建立了低、中压绕组“质量-弹簧”轴向固有振动模型,分析结果表明:绕组各阶轴向固有振动频率的平方与轴向预应力之间成线性正相关。
参考文献
[1]李林,单長吉.质量-弹簧-阻尼系统的二次型最优控制的实现[J]西安文理学院学报,2012,15(1):98.
[2]郑磊,张丽娟.电缆变压器短路时绕组轴向振动特性的探讨[J].信息通信,2011,113(3):150.
(作者单位:国网北京经济技术研究院徐州勘测设计中心)

