顶点Pk覆盖问题的研究综述

王利民 华景煜

摘要顶点覆盖问题是经典的NP完全问题，在排序、计算机网络等现实生活中有许多的应用.近几年来，许多研究者开始探究它的推广形式——顶点P_k覆盖（VCPP_k）问题，即寻找一个顶点子集，从拓扑结构图中删除后使得剩下的顶点导出的子图不包含P_k路，其中P_k是指包含k个顶点的路.本文简单介绍了VCPP_k问题的应用背景，归纳了它在近似算法、精确算法、参数化算法3个方面的主要研究进展，并分析了一些主要的方法和技巧.在此基础上，对VCPP_k问题及其相关问题的研究前景进行了展望.关键词顶点P_k覆盖；近似算法；精确算法；参数化算法

中图分类号TP391.7

文献标志码A

0 引言

顶点覆盖问题是一个经典的NP完全问题，它与团问题、独立集问题等可以互相转换，在排序、计算机网络等现实生活中有许多的应用.近几年来，许多研究者开始探究它的推广形式——顶点P_k覆盖（VCPk，k≥3）问题.这个问题是顶点删除问题的一个特殊类型.顶点删除问题就是寻找一个顶点子集，从拓扑图中删除这些顶点后，使得剩下的顶点导出的子图满足一个给定的特征.例如顶点P_k覆盖问题，即寻找一个顶点子集，从拓扑结构图中删除这个子集后使得拓扑图中剩下的顶点导出的子图不包含Pk路，其中Pk是指包含k个顶点的路.

无线传感器网络是当前信息领域中研究的热点之一，可用于特殊环境的信号采集、处理和发送.无线传感器网络是一种全新的信息獲取和处理技术，作为一种无处不在的感知技术，无线传感器网络广泛应用于军事、环境、医疗、家庭和其他商用及工业领域.在空间探索和反恐、救灾等特殊的领域，传感器技术和节点间的无线通信能力为无线传感器网络赋予了广阔的应用前景.

在无线传感器网络越来越广泛的现实生活应用中，人们主要关注的安全特性包括机密性、可靠性和数据的完整性等.由于传感器自身的计算能力、电源储备和处理信息的能力都有限，而且，它们通常部署在易受影响的区域，很容易被攻击者攻击或信息被窃取.传统的安全协议不能直接应用到无线传感器网络中，因此，就安全研究领域来说，如何设计无线传感器网络的安全协议成为一个很大的挑战.

许多学者在这方面进行了大量探究，例如，在传感器网络中，为了确保数据的完整性或数据来源认证，文献[1]就设计了一个安全协议.为了确保数据的完整性，推广的Canvas协议[2]提出在传感器形成的通信图中，对于每条长度为k-1的路径中至少要有一个顶点没有被捕获.因此，在传感器网络的部署和初始化期间，应确保至少有一个受保护的顶点存在于每个长度为k-1的路径中.又由于传感器之间需要传递信息，以及对传感器加以保护是需要费用的，为此在现实应用时还需要考虑传感器节点之间的连通性，以及合理设计安全协议尽量减少费用.更多的实际应用可以参考文献[3].

一般图上的权值最小VCPP_k问题和所含顶点数最少的VCPP_k问题都是NP完全问题.本文重点介绍VCPP_k问题的研究成果包括：无向图、有向图和特殊图的VCPP_k问题和参数化VCPP_k问题的相关算法，同时根据已有成果介绍一些可以值得研究的方向.下面给出VCPP_k问题的一些相关定义.

图G=（V，E）是一个含有n个顶点的图，V是G的顶点集，E是边集.

定义1（含顶点数最少的VCPP_k，简记MVCPk） 给定一个含有n个顶点的图G，求一个含顶点数最少的VCPP_k.

定义2（权值最小的VCPP_k，简记MWVCPP_k） 给定一个顶点带权的图G，求一个权值最小的VCPP_k.

一般图上的MVCPP_k和MWVCPP_k问题的前期研究主要集中在一些性质、近似算法和精确算法，其中也包括顶点连通性，即使得求得的VCPP_k集导出的子图是连通的.近几年，许多学者开始关注VCPP_k问题的参数化，参数化VCPP_k问题的定义如下：

定义3（参数化不带权的VCPP_k，简记PVCPk） 给定含有n个顶点的图G和一个非负整数k，能否在图中找到一个含顶点个数不超过k的VCPP_k.

如果一个参数化NP难问题在时间f（k）nO（1）内可解，其中f（k）是仅关于k的一个函数，那么称此问题是固定参数可解的（FixedParameter Tractable，简记FPT）[4].

本文第1节介绍无向图中VCPP_k问题的研究现状；第2节主要描述无向图中PVCPP_k问题的研究现状；第3节给出一些特殊图中VCPP_k问题的研究现状；第4节介绍有向图中VCPP_k问题的研究现状；最后通过分析和总结，给出VCPP_k问题研究中可以考虑的几个方面.

1 无向图中的VCPP_k问题

本节主要介绍无向图中VCPP_k问题的研究现状，主要包括近似算法、精确算法和MVCPP_k的上下界.

1.1 近似算法

由于VCPP_k问题是NP完全问题，除非P=NP，否则VCPP_k问题不可能有多项式时间算法，因此前期学者对最小VCPP_k问题的研究主要集中在多项式时间可解的近似算法.近似算法主要是在最坏的情况下找到问题的近似解与最优解的比值；即算法的近似度.近似算法主要的衡量指标之一就是近似度.下面主要分析MVCPP_k和MWVCPP_k问题的近似算法.对于MWVCPP_k问题，算法的近似度为近似解与最优解的权值的比值，对于MVCPP_k问题，近似度为近似解与最优解所含顶点数目的比值.

文献[5]利用以某概率选择顶点的方法得到MVCP3问题的一个近似比期望为2311的随机算法.Tu等[67]利用原始对偶算法或分层技巧分别给出权值最小的VCP3问题的一个2因子近似解.文献[6]通过在原图上添加悬挂边的方法，将权值最小的顶点覆盖问题归约到权值最小的VCP3问题，证明VCP3问题是NP难解的.

文献[8]首先利用逐步删除P_k的贪婪算法和添加顶点的方法给出了最小的连通VCPk问题的一个k2近似解，进而结合平面的划分和转移策略给出这个问题在单位圆盘图上的一个多项式时间近似格式的算法.这个算法的整体设计思路如下：首先，定义一个正方形区域使得这个区域包含图中的所有单位圆盘，再将这个区域划分成一些小的正方形.对每一个小正方形，定义它的中心区域和边界区域.其次，对于单位圆盘图，采用一个常因子的近似算法求得图的一个连通的VCPk集，使得这个近似解中每个顶点的权值至多是c，这里c是一个正的常数.然后，对于每个正方形的中心区域，枚举所有的VCPP_k集，仅仅考虑满足邻域条件的解，进而选择顶点权和最小的一个解，将此解记作局部最优解.通过对边界区域的选择，可以确保算法的输出结果是一个连通的VCPP_k集.最后将常因子近似解落在某个划分的边界区域的顶点集合与局部最优解合并.一般地，将正方形区域的左下角沿着45°角移位，每次移动2个单位就得到一个新的划分.其中采用转移策略是为了选取一个划分使得常因子近似解落在这个划分的边界区域的顶点集合的权和或顶点个数尽可能小，从而使得输出结果与最优解的比更小.而划分策略或分治法主要是将一个难以直接解决的大问题，分割成一些规模较小的相同问题，各个击破，分而治之，然后再利用这些子问题的解求出原问题的解.简言之，缩小问题规模，使子问题易求解.在假设图的围长至少是k的条件下，Li等[9]利用深度优先搜索法及逐步加点判断的方法提高了最小的连通VCPk问题在一般图上的近似比，即给出一个k近似解，其算法时间复杂度为O（n2）.

文献[10]提出最小连通有界VCPP_k的概念，并在假设图的度有界的条件下，利用增长划分的方法得到连通的VCPP_k问题在growthbounded图上的一个多项式时间近似格式的算法，但是此时不需要利用常因子近似解.文献[10]的主要思想是将图划分成一些聚类，然后对每一个聚类求局部解，进而合并这些解得到最后结果.

在假设图的最小度为2的情况下，Wang等[11]首先利用原始对偶算法和有关顶点加权的斯坦纳树的一个近似算法得到权值最小的连通VCP3问题的一个常因子近似解；其次利用文献[12]给出的最小连通顶点覆盖问题在单位圆盘图上的多项式时间近似格式算法的思想，结合一个类似c局部问题[13]的概念（c是一个正的常数），再利用平面上的划分和转移策略，给出权值最小的连通VCP3问题在单位圆盘图上的一个多项式时间近似格式的算法.

在现实世界中，为了观察某些复杂的环境，例如高山上或水里[14]，一些传感器就被放在不同的深度，这就形成了三维空间的网络，它可以模拟的数学模型是单位球图.根据平面上研究的一些结论和受到的启发，Wang等[15]提出一个弱c局部问题的概念（c是一个正的常数），并在顶点权值的光滑性条件下，利用高维空间的划分和转移技巧，给出权和最小的连通VCP3问题在单位球图上的一个多项式时间近似格式的算法.当球的半径不同时，上面的方法将不起作用.然而文献[16]在球的最大半径与最小半径的比值有界的条件下，利用局部搜索的方法给出最小的VCPP_k问题在球圖上的一个多项式时间近似格式的算法.

注意到在处理连通的VCPP_k问题时，主要包含常因子的近似解、多项式时间近似格式的算法和特殊拓扑结构图上的时间复杂度等3个方面.

对于求解常因子的近似解，一般地，先通过一些算法或技巧找到一个不连通的近似解，再结合求解斯坦纳树的算法或逐步添加顶点并判断的方法，进而得到连通的常因子近似解.或者，先利用深度优先搜索法或其他搜索法得到拓扑结构的支撑树，再对树的每一分支判断是否需要继续添加顶点，从而得到所求的结果.因此，以后在求解连通的常因子近似解时就可以参考这2种方法.而设计多项式时间近似格式的算法，主要采取划分策略和转移策略，以及增长划分策略2种方式，当图中顶点的位置信息已知时大部分采取划分和转移策略，这是处理这类问题常用的技巧和方法.然而在更一般的图上，如growthbounded图上，不需要利用常因子近似解，只知道图的部分信息，此时多采取增长划分.不管是那种划分策略，为了达到连通都需要使划分的小区域有重叠的部分，算法最关键的地方就是处理重叠部分.

1.2 精确算法

近似算法只能得到问题的近似解而无法得到精确解，甚至许多问题很难求得近似解.于是许多学者开展了对VCPP_k精确算法的研究.显然，通过枚举图中n个顶点的2n个子集就可以找到最小的VCPP_k.

对于VCP3问题，文献[5]利用分支定界法逐步减少图的顶点个数，从而求得MVCP3，其算法时间复杂度为O（1.517 1n），其中n是图G的顶点个数.Chang等[17]利用加权分治技术提出一个分支化简的算法，算法提高了上面的时间复杂度，其复杂度为O（1.465 8n）.文献[18]根据给出的一些有关分散集和VCP3结构特征，利用更多的化简规则和分支规则，提出了时间复杂度为O（1.465 6n）的精确算法，此时需要多项式空间；进一步利用动态规划技术改进算法，其时间复杂度为O（1.365 9n），但是需要指数空间.

1.3 MVCPP_k的上下界

2 无向图中的PVCPP_k问题

在实际应用中，图的结构是比较复杂的且图的顶点数n往往比较大，VCPP_k问题的所有精确算法都无法应用于实际.但是在很多实际应用中，VCPk的大小k比n小很多，而且有些应用不一定要找最小的VCPP_k，而只要求小于某个值的VCPP_k，于是许多研究者考虑研究VCPP_k问题的参数化.下面开始介绍无向图参数化VCPP_k问题的研究现状.

文献[4]采用迭代压缩技术证明一般图上的PVCP3问题是固定参数可解的，即对于固定的参数k，这个问题可以在时间O（2kk3.376+n4m）内得到它的解，其中n是图的顶点个数，m是图的边数，VCP3问题解的顶点个数至多是k.文献[24]利用化简规则和分支搜索技术给出PVCP3问题的一个FPT算法，其时间复杂度为O（1.817 2knO（1））.Chang等[25]也利用化简规则和分支搜索技术在多项式空间和指数空间中分别说明PVCP3问题是固定参数可解的，算法所执行完成的时间至多分别为O*（1.796 4k），O*（1.748 5k），这里O*的含义为：对于2个函数f和g，如果f（k，n）=O（g（k）·poly（n）），那么f（k，n）=O*（g（k）），其中poly（n）是n的多项式函数.对于VCP4问题，Tu等[26]也利用迭代压缩技术证明一般图上的PVCP4问题是固定参数可解的，时间复杂度为O（3kn4）.

VCPP_k问题核心化是参数化VCPP_k问题的重要研究内容.如果在求解VCPP_k问题之前，利用核心化算法对问题规模进行简化，将大大提高求解PVCPP_k的效率.对于VCP3问题，文献[27]得到一个大小为15k的核，文献[28]利用2次简化规则提高这个核到6k-6，Brause等[29]利用皇冠分解给出一个计算核的多项式时间的算法，通过算法得到图的2个不交的集合T1，T2，满足|T2|≤6·ψ3（G[T2]），其中T2为图G的核，可以看出此处核的上界为6k.最近，通过改进化简规则，文献[30]将该问题的核大小提高到5k.

3 特殊图中的VCPP_k问题

对于特殊图上的VCPP_k问题，许多学者也进行了大量的研究.某些特殊的应用对应一些在具有特殊性质的图上的VCPP_k问题，而特殊图上的VCPP_k问题比一般图上的VCPP_k问题更容易，使得在特定条件下解决VCPP_k问题显得更有意义.本节简要阐述各类特殊图中VCPP_k问题的研究现状.

1） 三正则图上的VCPP_k问题

三正则图是指图中所有顶点的度均为3的图，也称为立方图.在三正则图中，文献[31]给出了一些有关VCP3问题的结论：首先，利用归约证明在围长为3的三正则平面图中，最小VCP3问题的判定问题是NP完全的；其次，令ψ3（G）表示图G的最小VCP3集的顶点数，得出2n5≤ψ3（G）≤n2；最后，利用逐步删除顶点度为3的顶点的贪婪算法，给出最小VCP3问题的一个近似度为1.57的近似算法.在三正则图中，文献[32]给出了一些有关VCP4问题的结论：首先，利用归约证明最小VCP4问题的判定问题是NP完全的；其次，令ψ4（G）表示图G的最小VCP4集的顶点数，得出n4≤ψ4（G）≤n2；最后，利用Lovasz分解，给出最小VCP4问题的一个近似度为2的近似算法.

2） 完全图、路、圈、树上的VCPP_k问题

文献[33]从时间复杂度的角度考虑，在完全图、路和圈上分别可以在O（n·k）、O（n·k）和O（n·k2）时间内求出权值最小的VCPk问题的最优解，而在树上的时间和空间复杂度均为O（n·k）.文献[9]采取逐步判断树的分支是否含有Pk的方法，得到在树上可以在O（n2）时间内求出最小连通的VCPk问题的最优解.文献[34]通过寻找最长路以及逐步加点判断的方法可以在O（n）时间内找到权和最小的连通VCPk问题的最优解；进一步得到在包含唯一圈（圈的长度为r）的图上可以在O（nr）时间内找到这个问题的最优解.

3） 树宽有界的图的VCPP_k问题

在树宽有界的图中，文献[35]设计了一个动态规划算法可以求得MVCP3，其时间复杂度为4p·nO（1），其中树宽至多是p.文献[36]不仅提高了求MVCP3问题的时间复杂度3p·nO（1），而且针对连通的VCP3问题给出一个时间复杂度为4p·nO（1）的随机算法.

4 有向图中的VCPP_k问题

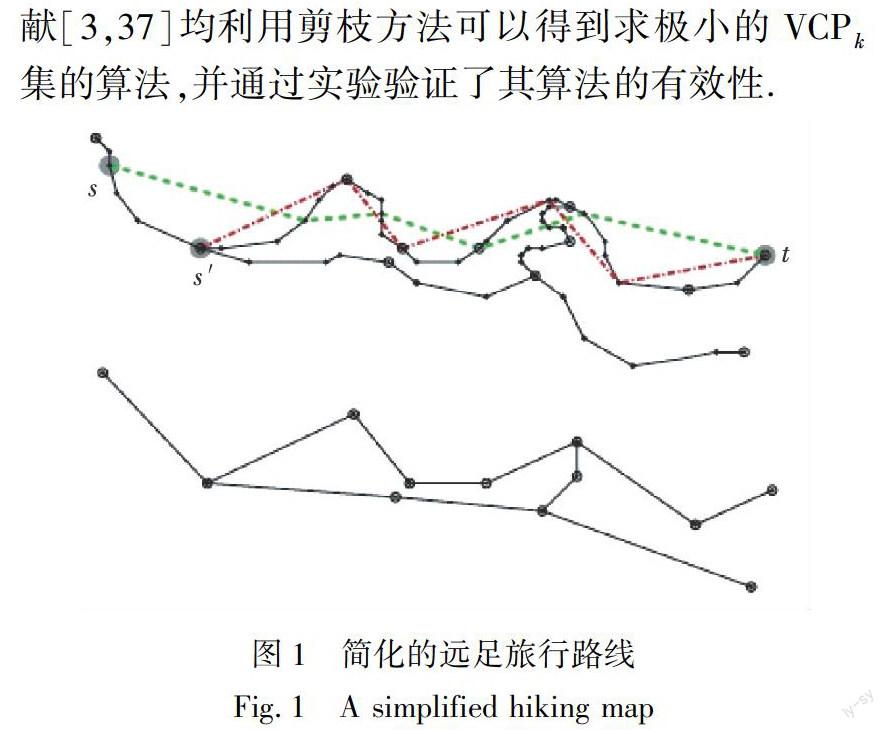
众多研究者探究VCPP_k的相关问题主要集中在无向的拓扑结构图上，对有向图的VCPP_k问题的研究进展较为缓慢，主要是考虑方向后难度会更大.然而，近年来，文献[3，37]分别从现实的生活环境和需求出发介绍了VCPP_k问题在有向图环境中的一些应用实例（图1）.例如：人们在远足旅行时会通过一些网站查询一下路线图，网站会发送几条建议远足路线，路线中的每个节点都标记的话会浪费很多带宽，因此，可以考虑只发送几个关键的节点信息，删除重叠的部分，使得路线图显得更清晰，便于出行者选择合适的路线.如图1，有2条出行路线红色s′→t和绿色s→t可供选择，只需选用灰圆圈标记的节点即可覆盖整个图（k=6时的情形）.在超大规模的图中，文献[3，37]均利用剪枝方法可以得到求極小的VCPP_k集的算法，并通过实验验证了其算法的有效性.

5 总结与展望

顶点覆盖问题是一类重要的NP完全问题，在排序、计算机网络等现实生活中有许多的应用.近几年来，人们开始关注它的推广形式——VCPk （k≥3）问题.本文着重阐述无向图中VCPP_k问题的研究现状.从中可以看出，前期较多的研究关注点是VCPP_k问题的性质和近似算法，而随着参数计算理论的产生，推动了VCPP_k问题的发展，使之成为目前阶段的研究热点.

通过对VCPP_k问题研究现状的总结和分析，可以使学者对VCPP_k问题有更全面的理解.当然对于VCPP_k问题，依然还有许多方面有待于我们进一步探究，主要可以从以下几个角度进行研究.

1）VCPP_k问题的算法研究

在一般图上对于权和最小的连通VCPP_k问题尚未有常因子近似解，是否可以根据已有结果及問题的自身特征寻求新颖的算法去求解，进而给出相应问题的一个多项式时间近似格式算法呢？ 处理这个问题的难点是如何使其连通.

对于权和最小的连通VCP3问题，所求的近似解是在最小度为2的情况下得到的，那么是否可以通过寻求新算法将图的最小度降为1？求解这个问题的多项式时间近似格式的算法时，有假设条件c局部或弱c局部以及顶点权值是光滑性的等，考虑到现实环境，不太实用，能否采用其他的方法将c局部等条件去掉？

2）VCPP_k问题的核心化

许多学者对无向图上VCPP_k问题的核心化研究已取得了一些结果，通过一系列局部简化规则和对图结构的分析，对核大小不断进行改进.希望能够通过深入分析已有结论和VCPP_k问题的结构，构造出更多的简化规则，从而提出更好的核心化算法.

3）VCPP_k问题的变形

近年来，一部分研究者探究VCPP_k问题的一个变体——k连通子图覆盖问题，即寻找一个顶点子集，从图中删除后使得图中剩下的顶点导出的子图不包含k个顶点导出的连通子图.可以看出这个问题比VCPP_k问题更具有一般性.在这方面的主要结论有：在假设图是连通的条件下，文献[9]利用深度优先搜索法、生成树及逐步加点判断的方法给出顶点连通的k连通子图覆盖问题的一个k近似算法.利用线性规划舍入方法很容易得到权和最小的k连通子图覆盖问题的一个k近似解.然而在假设图的围长至少是k的情况下，文献[38]提高了这个问题的近似比，首先利用图的拓扑结构，并结合顶点的度权函数给出一个近似比，其次，利用类似分层的方法又得到一个近似比，两者均为k-1.除了这2种情况有以上结果外，顶点不连通、不加权和顶点连通以及加权等情况尚未有人探讨，而且就现阶段的研究现状来看，对于有关k连通子图覆盖问题的多项式时间近似格式算法还没有研究者去探索，这可能也是一个比较好的研究方向.

4）VCPP_k问题的随机算法

随机化是现代计算机科学最重要的方法之一，近几十年来被广泛地应用于计算机科学的各个领域.在这些应用的背后，是一些共通的随机化原理.我们是否可以利用一些重要的随机算法的设计思想和理论分析，借助一些概率论工具及其在算法分析中的应用，从新的角度探索VCPP_k问题或k连通子图覆盖问题呢？

5） 特殊图上的VCPP_k问题

根据一些特定的应用，对于特殊图上VCPP_k问题的研究也很有意义.本文列举了一些特殊图上的VCPP_k问题，可以对这些问题的算法做进一步的研究，提出更有效的算法，或者对由实际应用而转化的特殊VCPP_k问题进行研究.

参考文献

References

[1] Menezes A J，Van Oorschot P C，Vanstone S A.Handbook of applied cryptography[M].Boca Raton：CRC Press，1996

[2] Novotny M.Design and analysis of a generalized canvas protocol[C]∥IFIP International Workshop on Information Security Theory and Practices，2010：106121

[3] Funke S，Nusser A，Storandt S.On kpath covers and their applications[J].The VLDB Journal，2014，25（1）：103123

[4] Tu J H.A fixedparameter algorithm for the vertex cover P3 problem[J].Information Processing Letters，2015，115（2）：9699

[5] Kardos F，Katrenic J，Schiermeyer I.On computing the minimum 3path vertex cover and dissociation number of graphs[J].Theoretical Computer Science，2011，412（50）：70097017

[6] Tu J H，Zhou W L.A primaldual approximation algorithm for the vertex cover P3 problem[J].Theoretical Computer Science，2011，412（50）：70447048

[7] Tu J H，Zhou W L.A factor 2 approximation algorithm for the vertex cover P3 problem[J].Information Processing Letters，2011，111（14）：683686

[8] Liu X L，Lu H L，Wang W，et al.PTAS for the minimum kpath connected vertex cover problem in unit disk graphs[J].Journal of Global Optimization，2013，56（2）：449458

[9] Li X S，Zhang Z，Huang X H.Approximation algorithm for the minimum connected kpath vertex cover problem[C]∥International Conference on Combinatorial Optimization and Applications，2014：764771

[10] Chu Y，Fan J X，Liu W J，et al.PTAS for minimum kpath connected vertex cover in growthbounded graphs[C]∥International Conference on Algorithms and Architectures for Parallel Processing，2014：114126

[11] Wang L M，Zhang X Y，Zhang Z，et al.A PTAS for the minimum weight connected vertex cover P3problem on unit disk graphs[J].Theoretical Computer Science，2015，571：5866

[12] Zhang Z，Gao X F，Wu W L.PTAS for connected vertex cover in unit disk graphs[J].Theoretical Computer Science，2009，410（52）：53985402

[13] Jiang T，Wang L S.An approximation scheme for some steiner tree problems in the plane[J].Networks，1996，28（4）：187193

[14] Akyildiz I F，Pompili D，Melodia T.Underwater acoustic sensor networks：Research challenges[J].Ad Hoc Network，2005，3（3）：257279

[15] Wang L M，Du W X，Zhang Z，et al.A PTAS for minimum weighted connected vertex cover P3 problem in 3dimensional wireless sensor networks[J].Journal of Combinatorial Optimization，2017，33（1）：106122

[16] Zhang Z，Li X T，Shi Y S，et al.PTAS for minimum kpath vertex cover in ball graph[J].Information Processing Letters，2017，119：913

[17] Chang M S，Chen L H，Hung L J，et al.An O*（1.465 8n）time exact algorithm for the maximum boundeddegree1 set problem[C]∥Proceedings of the 31st Workshop on Combinatorial Mathematics and Computation Theory，2014：918

[18] Xiao M Y，Kou S W.Exact algorithms for the maximum dissociation set and minimum 3path vertex cover problems[J].Theoretical Computer Science，2017，657（A）：8697

[19] Bresar B，Kardos F，Katrenic J，et al.Minimum kpath vertex cover[J].Discrete Applied Mathematics，2011，159（12）：11891195

[20] Jakovac M.The kpath vertex cover of rooted product graphs[J].Discrete Applied Mathematics，2015，187（C）：111119

[21] Zuo L C，Zhang B T，Zhang S Q.The kpath vertex cover in product graphs of stars and complete graphs[J].International Journal of Applied Mathematics，2016，46：97103

[22] Brause C，KrivosBellus R.On a relation between kpath partition and kpath vertex cover[J].Discrete Applied Mathematics，2017，223：2838

[23] Bhavani P D，Kumar K V，Satyanarayana S.An investigation on some theorems on kPath vertex cover[J].Global Journal of Pure and Applied Mathematics，2016，12（2）：14031412

[24] Katrenic J.A faster FPT algorithm for 3path vertex cover[J].Information Processing Letters，2016，116（4）：273278

[25] Chang M S，Chen L H，Hung L J，et al.Fixedparameter algorithms for vertex cover P3[J].Discrete Optimization，2016，19：1222

[26] Tu J H，Jin Z M.An FPT algorithm for the vertex cover P4 problem[J].Discrete Applied Mathematics，2016，200（C）：186190

[27] Fellows M R，Guo J，Moser H，et al.A generalization of Nemhauser and Trotters local optimization theorem[J].Journal of Computer and System Sciences，2011，77（6）：11411158

[28] Chen J E，Fernau H，Shaw P，et al.Kernels for packing and covering problems[C]∥Frontiers in Algorithmics and Algorithmic Aspects in Information and Management，2012：199211

[29] Brause C，Schiermeyer I.Kernelization of the 3path vertex cover problem[J].Discrete Mathematics，2016，339：19351939

[30] Xiao M Y，Kou S W.Kernelization and parameterized algorithms for 3path vertex cover[C]∥International Conference on Theory and Applications of Models of Computation，2017：654668

[31] Tu J H，Yang F M.The vertex cover P3 problem in cubic graphs[J].Information Processing Letters，2013，113（13）：481485

[32] Li Y C，Tu J H.A 2approximation algorithm for the vertex cover P4 problem in cubic graphs[J].International Journal of Computer Mathematics，2014，91（10）：21032108

[33] Bresar B，KrivosBellus R，Semanisin G，et al.On the weighted kpath vertex cover problem[J].Discrete Applied Mathematics，2014，177：1418

[34] Li X S，Zhang Z，Huang X H.Approximation algorithms for minimum （weight） connected kpath vertex cover[J].Discrete Applied Mathematics，2016，205：101108

[35] Tu J H，Wu L D，Yuan J，et al.On the vertex cover P3 problem parameterized by treewidth[J].Journal of Combinatorial Optimization，2016，31（1）：112

[36] Bai Z W，Tu J H，Shi Y T.An improved algorithm for the vertex cover P3 problem on graphs of bounded treewidth[J].arXiv eprint，2016，arXiv：1603.09448

[37] Bhavan P D，Krishna G V，Thota N.Minimum kpath vertex using pruning algorithm[J].International Journal of Scientific Engineering and Technology Research，2014，3（46）：94199422

[38] Zhang Y P，Shi Y S，Zhang Z.Approximation algorithm for the minimum weight connected ksubgraph cover problem[J].Theoretical Computer Science，2014，535：5458